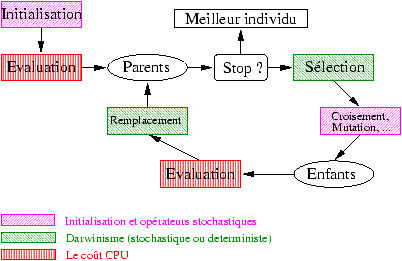
Figure 8.1: Squelette d'un algorithme évolutionaire



Il est important de noter que le coût CPU essentiel de ces algorithmes provient de l'étape d'évaluation (calcul des performances) : les tailles de populations sont de l'ordre de quelques dizaines, le nombre de générations de quelques centaines, ce qui donne lieu à quelques dizaines de milliers de calculs de F.
Figure 8.1: Squelette d'un algorithme évolutionaire
Dans le cadre de l'optimisation paramétrique, on peut bien entendu appliquer les mêmes opérateurs d'échange de coordonnées. On peut également -- et c'est en général bien plus efficace -- ``mélanger'' les deux parents par une combinaison linéaire. On parle alors de croisement arithmétique :
Figure 8.2:
| (X,Y) |
|
a X + (1 - a) Y , a = U[0,1] |
| (X,Y) |
|
ai Xi + (1 - ai) Yi , ai = U[0,1] |
| (b1, b2, ..., bN) |
|
(b1, b2, ..., 1-bl, bl+1, ..., bN) |
| s := s exp(t N(0,1)) |
| Xi := Xi + N(0,s) |
Le tirage de roulette présente toutefois de nombreux inconvénients, en particulier reliés à l'échelle de la fonction performance : alors qu'il est théoriquement équivalent d'optimiser a F + b et F pour tout a > 0, il est clair que le comportement de la sélection par roulette va fortement dépendre de a dans ce cas. C'est pourquoi cette sélection est presque totalement abandonnée aujourd'hui.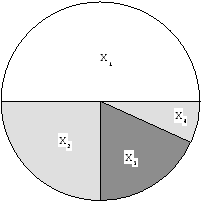
Figure 8.3: Sélection par tirage de roulette : cas de 4 individus de performances respectives 50, 25, 15 et 10. Une boule est ``lancée'' dans cette roulette, et l'individu dnas le secteur duquel elle s'arrête est sélectionné.
Lorsque la durée d'un calcul de performance varie d'un calcul à l'autre (que ce soit en raison de conditions de calcul différentes, ou de par l'hétérogénéité des processeurs utilisés), le gain apporté par ce schéma de parallélisation peut toutefois se dégrader, l'ensemble des processeurs devant alors attendre le plus lent d'entre eux. Une gestion plus fine de la distribution des calculs (à l'aide d'une liste de calculs à effectuer, un processeur recevant un nouveau calcul dés la fin du calcul précédent) permet de limiter ce phénomène sans complètement le suprimer en fin de génération. De plus, la tolérance aux pannes est nulle : si un processeur s'arrête pour une raison quelconque, l'ensemble de l'algorithme se mettra en attente du résultat manquant.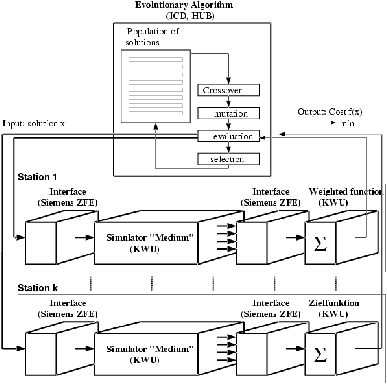
Figure 8.4: Distribution des calculs de performance, (c) Th. Bäck, ICD, Dortmund.
Mais même lorsque les sous-populations utilisent exactement les mêmes paramètres, la dispersion topologique, fonction du mode de migration choisi (i.e. entre voisins uniquement, ou avec un échange généralisé), a pour effet de préserver la diversité génétique plus longtemps. En effet, il est important de noter qu'il ne s'agit pas ici de la simple parallélisation de l'algorithme séquentiel, mais d'un algorithme à la dynamique totalement différente. Ceci rend en particulier difficiles les comparaisons avec les versions séquentielles, et biaise les tentatives d'estimation du gain.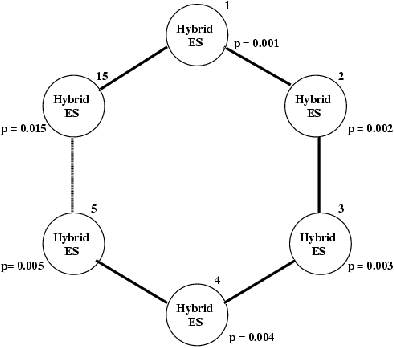
Figure 8.5: Exemple de modéle en îlots -- le paramètre de mutation est différent à chaque noeud, (c) Th. Bäck, ICD, Dortmund.
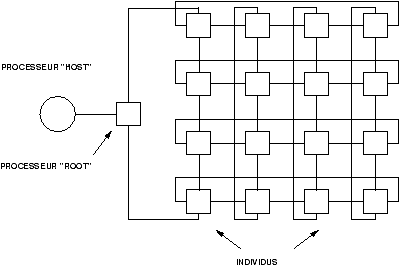
Figure 8.6: Population totalement distribuée, répartie sur une grappe de stations arrangées en topologie torique. Sur chaque noeud se trouvent quelques individus, qui se reproduisent localement.
| Entrées | Sortie | |||||||
|
® |
|
||||||
| Figure 1 : Un problème direct | ||||||||
| Entrées | Sortie | ||||||||||
|
® |
|
|||||||||
| Figure 2 : Un problème inverse du problème de la Figure 1. | |||||||||||
Une approche possible repose sur la notion de Diagrammes de Voronoî : l'espace de recherche est l'ensemble des listes de taille variable de sites de Voronoî auxquels est associé une vitesse de propagation. Le pavage du sous-sol par les cellules de Voronoî correspondantes réalise alors une disposition des vitesses de propagation ``constantes par gros morceaux'' dans le sous-sol -- ce qui est déjà plus réaliste (voir Figure 8.7. De plus, la complexité du maillage n'intervient pas sur la taille de l'espace de recherche. Les détails sur cette représentation et les opérateurs associés (qui se devinent aisément), ainsi que des exemples de résultats obtenus sur ce problème inverse (avec un algorithme séquentiel!) peuvent être trouvés dans l'article [SAB98].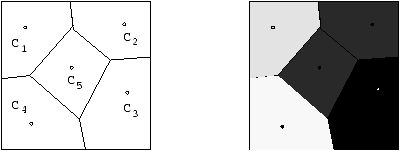
Figure 8.7: Exemple de représentation de Voronoï. Le génotype est la liste des sites de Voronoï munis chacun d'un scalaire (la vitesse en ce site). Le phénotype est obtenu par construction du diagramme de Voronoï correspondant : un point du domaine a la vitesse du site de Voronoï le plus proche de lui.


