Chapter 7 Ecriture de programmes parallèles
Pour l'écriture de code parallèle
on peut soit
paralléliser un code séquentiel (automatiquement),
soit ordonnancer des tâches parallèles à la main.
La difficulté est que
l'efficacité dépend de l'architecture de la machine cible
et de l'algorithmique du problème.
La morale est qu'il faut
bien réfléchir à l'algorithmique sous-jacente avant de se lancer
dans l'ordonnancement de tâches, l'optimisation du code etc. On pourra
se reporter à [LER92] pour plus de détails.
7.1 Méthodes classiques
Dans le génie logiciel parallèle traditionnel,
les notions importantes sont celles de tâche, processus
et processeur. Une tâche est un ensemble d'instructions séquentielles
qui représentent de façon logique une petite étape de calcul, insécable.
Un processus est aussi une abstraction logique: c'est un ensemble de tâches
organisées de façon séquentielle.
On obtient un code parallèle à partir d'un algorithme, en procédant
par un certain nombre d'étapes, que l'on nomme souvent
partitionnement, coordination et enfin affectation. Tout ceci va être
essentiellement décrit à travers un certain nombre d'exemples.
7.1.1 Partitionnement
Le partitionnement consiste à essayer
de trouver des candidats à la parallélisation. On commence
par essayer de décomposer le problème en un certain nombre de tâches.
Puis on affecte les tâches à un ensemble de processus. En général,
une tâche effectue une communication ou une synchronisation. Quand la tâche
est petite (en temps d'exécution), on parle de parallélisme à grain
fin. Quand la tâche augmente de taille, on parle de grain moyen puis
de gros grain: c'est le cas quand un processus contient une seule tâche
et une seule synchronisation avec les autres processus.
Cela peut se faire par décomposition de domaines:
diviser les données, puis les calculs
correspondants. Cela peut aussi se faire par
décomposition fonctionnelle: diviser les calculs, puis les données
correspondantes.
Exemple 1
Considérons par exemple un schéma explicite d'ordre 1 pour résoudre une
forme de l'équation des ondes bidimensionnelle. Supposons que l'on
dispose de p processeurs, et que l'on ait discrétisé le problème
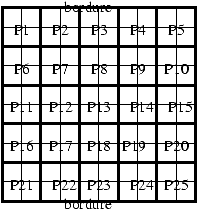
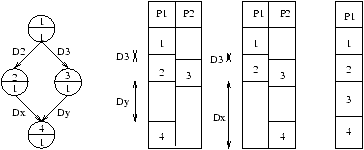
par une grille de n × n points comme indiqué sur la figure
7.11
. Le calcul de la valeur du champ de pression
u au point de coordonnées (i,j) (1 £ i, j £ n-1), à l'itération
t+1, ut+1(i,j) dépend
uniquement des valeurs de ses quatre voisins ut(i-1,j), ut(i,j-1),
ut(i+1,j) et ut(i,j+1) ainsi que de ut(i,j).
Figure 7.1: Partionnement d'un schéma explicite 2D
Alors, chaque processeur Pi (1 £ i £ p) aura une portion, comme indiqué
sur la figure 7.1, de la grille, et n'aura à se synchroniser, et
à échanger de l'information que sur le périmètre de chaque domaine.
.3cm
Un point important à toujours garder en tête quand il s'agit de
performances, est la loi d'Amdahl.
Exemple 1 suite
Considérons par exemple un calcul simple sur la grille n × n avec
p processeurs, évoqués précédemment. Supposons que ce calcul soit
composé de deux sous-calculs; un premier qui agit sur chaque point de la grille,
et ce de façon complètement indépendante de ses voisins, et un deuxième,
qui additionne toutes les valeurs à chaque point de la grille. Par exemple,
la première partie est un calcul de carré, la deuxième une somme, le tout
faisant un calcul d'énergie au carré
(qui peut être utile pour la validation numérique
du programme, ou du schéma). La première partie prendra donc un temps de
n2/ p. Une façon de programmer la deuxième partie est de séquentialiser
entièrement le calcul de la somme globale, qui va alors prendre un temps de
n2 (indépendant de p!). Le temps de l'algorithme séquentiel aurait
été de 2n2 alors que le temps mis par cet algorithme est de n2/ p
+2n2, donc l'accélération obtenue est d'au plus 2p/ p+1,
c.a.d. au plus de 2 quel que soit le nombre de processeurs que l'on
ait à disposition.
.3cm
C'est une conséquence simple de la loi d'Amdahl qui s'énonce comme suit.
Si on a un calcul dont s pourcent est séquentiel, et qui s'exécute sur
p processeurs, alors l'accélération du calcul complet par rapport à
un calcul séquentiel sera au maximum de,
c'est-à-dire que même dans le cas où on dispose d'une infinité de
processeurs, l'accélération maximale sera de 1/ s. Conséquence: même
si on parallélise 80 pourcent d'un code (le reste étant séquentiel),
on ne pourra jamais dépasser, quel que soit la machine cible, une accélération
d'un facteur 5!
Exemple 1 suite
En fait, on pouvait faire bien mieux dans notre exemple. Tous les processeurs peuvent,
en même temps, calculer une somme partielle locale. Puis une somme séquentielle
de p sommes partielles, prenant un temps2
de p. L'accélération est maintenant de 2 p n2/ 2 n2 + p
qui est presque linéaire en le nombre de processeurs (quand n est grand par
rapport à p).
Décomposition de données - Exemple 2
On a vu la transformée de Fourier
rapide à la section 5.2.2. Ici on va examiner des
parallélisations possibles, dans le cas du calcul bidimensionnel.
Le réseau que nous considérerons dans toute la suite est
composé de N (N ³ 2) stations nommées P1, P2, ···, PN.
La donnée de départ est une matrice complexe carrée M=(Mi,j)1 £ i,j £ K
de taille K ×
K (N divise K), entièrement stockée dans la mémoire locale de P1.
On veut construire des algorithmes qui répartissent au mieux le travail sur
les P1, P2, ···, PN de telle façon qu'à la fin de leur exécution,
la transformée de Fourier M se trouve stockée dans la mémoire
locale de P1.
On considérera que les performances de nos algorithmes ne dépendront que
des données suivantes :
- le temps d'un envoi d'un message, sans compter l'attente éventuelle d'un partenaire
pour la communication,
est le débit g
multiplié par
la taille en nombre de complexes du tableau envoyé plus le temps de latence d.
- le temps d'un cycle sur Pi (1 £ i £ N) est de ai (une constante).
On examine d'abord l'algorithme A suivant, inspiré de la solution naturelle en mode SIMD.
P1 (le maître) crée
des processus ``esclave'' sur chacune des autres stations (Pi, 2
£ i £ N) puis envoie
à chacune d'entre elles le ième paquet de K/ N lignes
de la matrice M. P1
exécute ensuite fft sur les K/ N premières lignes de M puis se met en attente
des transformées
de Fourier exécutées sur chaque autre paquet de K/ N lignes de M par
les esclaves. Une fois reçues et
stockées dans la matrice N, P1 envoie
à chaque esclave Pj le jème paquet de K/ N colonnes
sur lesquelles Pj
effectue encore une fois fft. Enfin P1, qui a calculé pendant ce temps la transformée
du premier paquet de colonnes, réceptionne les transformées effectuées par les autres stations
et les stocke dans M.
Le pseudo-code pour le maître est,
struct complex M[K][K];
int tids[N-1];
fft_une_dimension()
{ int i;
for(i=1; i<=N-1; i++)
{
pkcmplx(&M[i*K/N][0],K*K/N,1);
pvm_send(tids[i-1],0);
}
for(i=0; i<K/N; i++) fft(M[i],K);
for(i=1; i<=N-1; i++)
{
pvm_recv(tids[i-1],0);
upkcmplx(&M[i*K/N][0],K*K/N,1);
}
}
transpose()
{ int i,j;
for(i=0; i<K; i++)
for(j=0; j<i; j++)
M[j][i]=M[i][j];
}
maitre()
{ pvm_spawn("esclave",NULL,0,0,N-1,tids);
fft_une_dimension();
transpose();
fft_une_dimension();
transpose();
}
Le pseudo-code pour les esclaves est,
fft_une_passe()
{ int i,tid=pvm_parent();
complex T[K/N][K];
pvm_recv(tid,0);
upkcmplx(T,K*K/N,1);
for(i=0; i<K/N; i++) fft(T[i],K);
pkcmplx(T,K*K/N,1);
pvm_send(tid,0);
}
esclave()
{
fft_une_passe();
fft_une_passe();
}
Décomposition fonctionnelle - Exemple 3
On peut remarquer que, en supposant i,j£ K/ 2, on a:
|
Mij |
= |
|
| |
= |
|
| |
|
|
| |
= |
|
|
æ
ç
ç
ç
ç
ç
è |
|
|
|
|
M2k,2l e |
|
+ |
|
|
|
|
M2k+1,l e |
|
|
| |
|
|
| |
|
|
| |
= |
|
|
æ
ç
ç
ç
è |
M |
ijpp +
e |
|
M |
ijip +
e |
|
M |
ijpi +
e |
|
Mijii |
ö
÷
÷
÷
ø |
|
Le principe de la décomposition fonctionnelle est le même que celui dans
le cas de la FFT unidimensionnelle (section 5.2.2):
les esclaves sont créés en parallèle jusqu'à
l'étape h où les feuilles calculent la FFT séquentiellement.
Dans une deuxième phase les esclaves remontent la FFT grâce à la propriété
que l'on vient de prouver.
On peut cependant minimiser
le temps inactif de chaque station en ne ``spawnant'' jamais la quatrième branche
mais en conservant cette exécution locale.
7.1.2 Coordination
Elle peut s'organiser de façons très différentes selon les besoins:
locale où globale (avec un centralisateur ou pas),
décidée de façon statique ou dynamique, et enfin
synchrone ou asynchrone (communications bloquantes ou pas).
Deux principes essentiels sont d'assurer un maximum de
recouvrement calcul et communication dans le cas
où les communications
sont asynchrones (ou non-bloquantes) et d'assurer une certaine localité
des données afin de limiter le nombre et la taille des communications.
Exemple 2 suite
Par exemple, le schéma explicite de la section 7.1.1
a un temps de communication par processeur de l'ordre de 4n/ p
(le périmètre de chaque domaine) pour un
temps de calcul par processeur de l'ordre de n2/ p. Par contre, ayant
quatre voisins en général avec qui communiquer, la coordination globale à
tendance à beaucoup attendre les retardataires voisins. On pourrait en fait
faire ici des communications asynchrones (dont les réceptions seraient affectées
à une bordure de chaque domaine, sans synchronisation intempestive).
Une autre
solution est de changer la géométrie des domaines. Par exemple, on pourrait
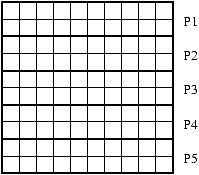
subdiviser la grille 2D en bandes horizontales comme indiqué sur la figure
7.2
Figure 7.2: Une autre organisation des domaines pour un schéma explicite simple
La taille des communications par processeurs est alors plus grande en général
et est indépendante de p (de l'ordre de 2n). Par contre, n'ayant qu'au maximum
deux voisins, il est possible de moins synchroniser certains calculs.
Les temps
de communication pour la décomposition de domaine de la figure
7.1 peuvent être décomptés comme suit.
Le temps de communication du maître est 2(N-1)(K2/ Ng+d) pour les envois
et 2(N-1)K2/ Na1 pour les réceptions. Le temps de communication d'un esclave est
de même 2(K2/ Ng+d) et 2K2/ Nai respectivement.
L'esclave numéro Pi attend i-1 compactages et envois pour la réception des données
lors de sa première passe. Il attend en outre la transposition et N-i+1
décompactages et réceptions
lors de sa deuxième passe.
Le maître n'attend pas pour la réception des données des esclaves dès lors que les esclaves
sont aussi rapides que le maître et que le nombre d'esclaves est supérieur ou égal à deux.
Par contre si les ai étaient différents, le maître devrait
attendre les esclaves les plus lents.
Donc, si on suppose que les esclaves sont aussi rapides que le maître,
le temps de calcul pour cet algorithme
est le temps de calcul du maître plus son temps de communication.
- spawn : t
- transpose : (K2-2K)a1
- fft : 2K/ Nq(K log K)a1
- envois : 2(N-1)(K2/ Ng+d)
- réceptions : 2(N-1)K2/ Na1
- compactage et décompactage : 4(N-1)K2/ Na1
Si les ai étaient
différents, ce serait la plus lente des stations qui imposerait la cadence. On pourrait modifier
l'algorithme en connaissant les coefficients, de telle façon à répartir plus de lignes
(respectivement colonnes) sur les stations les plus rapides.
Plus précisément Pi devrait traiter 1/ai/ S 1/aiK lignes.
.3cm
Exemple 2 amélioré
La communication recouvre donc bien les calculs dans l'exemple
précédent. La coordination était
globale. On peut ``localiser'' un peu celle-ci, afin
que chaque esclave gère lui-même l'envoi de ses parties de colonnes
directement (sans passer par P1) aux stations correspondantes.
Une fois la transformée en ligne calculée sur une station Pi (paquet de
ligne pi),
on peut exécuter les pvm_send des paquets de colonnes cj vers les
P1, ···, Pi-1,
puis dans un ordre quelconque les pvm_recv des paquets de colonnes ci appartenant
aux stations P1, P2, ···, Pi-1, Pi+1, ··· PN et
les pvm_send restants (colonnes ci+1, ···, cN). Ceci assure qu'il
n'y aura
pas d'interblocage.
On y gagne en temps de communication,
(N-1)(K2/ Ng+d) pour les envois
et (N-1)K2/ Na pour les réceptions, plus en temps de compactage/décompactage :
2(N-1)K2/ Na.
.3cm
Exemple 3 suite
Dans l'exemple 3 de la section 7.1.1,
le temps de communication de la décomposition fonctionnelle (en ``spawnant''
quatre fils à chaque fois) est de 2(h-1)[K2(g+a)+d].
Celui où on ne ``spawne'' que trois fils est de
2h[3K2/ 4(g+a)+d]. Il est supérieur à celui de
l'algorithme par décomposition de données dès que h³ 3.
Le temps de calcul de la procédure séquentielle fft pour Pi aux
feuilles (dont la taille est K/ 2h-1) est
soit un ratio favorable de 1/ 2log N pour la décomposition fonctionnelle
vis-à-vis de
l'algorithme par décomposition de données (de 3/ 8log N si on avait
``spawné'' trois fils seulement).
Il faut cependant encore
ajouter la remontée du calcul de la FFT, q(K2/ 4n)ai pour un esclave Pi
à la profondeur 0£ n<h.
7.1.3 Equilibrage de charges et tolérance aux pannes
Supposons ici que les ai (pour l'algorithme de FFT bidimensionnel)
puissent être très
différents les uns des autres et ne soient connus par aucun des Pi.
Autorisons nous également pour un nombre de stations
t < N - 1 parmi les P2 à PN un ai égal à plus l'infini,
modélisant ainsi la panne juste après la connection à pvmd
(panne immédiate). Dans ce cas, on supposera qu'il n'y a aucun
moyen pour aucune des stations de détecter la panne d'une autre des stations.
Quand on ne connaît pas, et quand on ne peut pas déterminer les processeurs
morts, ou leurs vitesses relatives, l'allocation statique des tâches
que l'on a réalisé aussi bien pour l'exemple 2 que
pour l'exemple 3 de 7.1.1
n'est pas bonne. Si un des ai est égale à +¥ alors le
maître se bloque, et si les ai sont très différents cela
occasionne beaucoup d'attente.
On donne ici deux méthodes simples pour résoudre le problème. On conseille,
pour plus de détails,
la lecture de [Lyn96].
Une solution par ``timeout''
Le principe est de décider
qu'après le temps t les stations qui n'ont pas répondu
sont mortes et alors de les ignorer.
Le problème est de choisir t. Si t est tel que l'on en déduise
que toutes sont mortes, on double t et on recommence, ainsi de suite.
Comme on a supposé
que toutes les stations ne pouvaient pas mourir, il existe une borne au-dessus
de laquelle l'une d'entre elles répondra.
Une solution par une architecture ``client/serveur''
L'idée est de simuler une mémoire partagée (contenant essentiellement M) par un
``serveur'' (P1). Les accès par les autres stations (``clients'') se font à travers
des communications asynchrones : des messages avec le TAG ``write'' correspondent à
une demande faite par un client d'écrire son paquet (de lignes ou de colonnes) dans M,
stockée localement dans la mémoire de P1. Des messages avec le TAG ``read'' correspondent
à une demande de lecture d'un paquet de lignes faite par un client au serveur P1. On
peut implémenter ce client/serveur en
PVM par signaux ou par ``active polling''3
.
La modification de l'algorithme par décomposition de données (section
7.1.1) est alors comme suit :
- En plus de M, P1 gère une collection de drapeaux (variables booléennes) : un drapeau
d(l) (respectivement d(c))
est associé à chaque ligne l (respectivement à chaque colonne c) de M. Ces drapeaux
sont utilisés pour savoir (et faire savoir) si une ligne (respectivement une colonne)
est utilisée par un client. Les drapeaux sont initialement à faux.
- Chaque esclave demande la ligne 1, puis la ligne 2 etc. Le premier qui l'obtient fait
son calcul de fft puis demande à réécrire dans M la ligne correspondante. Quand
tous les drapeaux des lignes sont à vrai, les esclaves font la compétition pour calculer
les transformées en colonne cette fois-ci.
Supposons d'abord que chacun des clients demande d'abord au serveur la valeur
du drapeau de la ligne 1, de la ligne 2, etc. jusqu'à en trouver un à la valeur faux.
A ce moment là, le client demande la lecture de la ligne correspondante (ce qui met
automatiquement le drapeau correspondant à vrai).
Le problème est d'avoir dissocié le test du drapeau, de sa modification (problème
d'atomicité, et donc de cohérence de l'état du système):
si on a un processus
qui se glisse entre le test et la demande de lecture, pour faire
lui-même le test, on peut avoir deux processeurs exécutant le même calcul.
Supposons maintenant que les clients demandent au serveur la première
ligne (ou colonne) dont le drapeau est à faux. Le serveur étant purement séquentiel,
quelque soit la rapidité des différents clients, il répond aux requêtes dans
un certain ordre (propriété de séquentialisation assurant la cohérence).
Le serveur ne peut plus donner la même ligne (ou colonne) à deux clients. Les calculs
sont donc répartis sans redondance.
Cette méthode résoud le problème des pannes
immédiates, mais pas d'une panne qui pourrait se produire à n'importe
quel moment du calcul.
Un client qui tombe en panne après avoir lu une ligne (ou colonne)
aura réservé le drapeau correspondant et finalement
va bloquer le calcul global. Par contre en cas de pannes immédiates le calcul ira jusqu'à
son terme si au moins un client reste actif, car les clients en panne immédiate ne peuvent
pas lire de ligne (ou colonne).
La compétition entre les processeurs avantage en moyenne les plus rapides : cette méthode sera
plus efficace quand les ai sont différents, que celles utilisant un
partitionnement statique (qui n'équilibre pas bien les charges).
7.1.4 Contention et Bande Passante
Dans le schéma explicite, exemple 1
de la section 7.1.1, chaque processeur
doit envoyer un volume de données égal à son périmètre à chacun de
ses 2, 3 ou 4 voisins (de l'ordre de 4n/ p).
Il est possible (en général quand on passe aux problèmes
tri-dimensionnels), que la bande passante du réseau, ou du bus d'interconnexion
soit dépassé par le volume de données ayant à transiter, entraînant ainsi
une séquentialisation et un délai. Il peut s'avérer utile à ce moment là
de changer la géométrie des domaines, ou de segmenter les envois de messages.
La solution où les domaines sont des bandes horizontales est moins bonne de ce
point de vue là car le périmètre, donc le volume de communication est de
l'ordre de 2n (indépendant de p).
7.1.5 Agglomération
Le principe est d'essayer
d'augmenter la granularité des calculs faits en parallèle,
de répliquer les calculs ou les données (quand la communication des données ou
des résultats est trop chère), et en somme
d'éviter au maximum les communications. Par exemple, dans certains problèmes
et sur certaines architectures, il peut être trop couteux d'echanger certaines
données. On copie alors toutes les données (au démarrage) sur chaque
station du réseau. Le problème est alors que l'on ne peut plus gérer
des gros problèmes qui eux ont besoin de plus de mémoire qu'un ordinateur
séquentiel peut adresser.
7.1.6 Affectation
C'est la phase où on essaie de déterminer comment sont réparties
les processus sur les processeurs. Cela peut se faire de différentes manières,
selon que l'on connaisse ou pas la topologie de communication (et les coûts
associés). Le problème est un cas particulier
du problème d'ordonnancement de tâches parallèles pour lequel on donne
quelques pointeurs dans la section suivante.
Exemple 4
Prenons ici l'exemple classique de la multiplication de matrices.
En mémoire partagée
le code suivant effectue une simple multiplication de matrices
par blocs colonnes:
for (i=1;i<=n;i++)
for (j=1;j<=n;j++)
for (k=1;k<=n;k++)
C_{i,j}=C_{i,j}+A_{i,k}B_{k,j};
On peut aussi organiser la localité des données par blocs rectangulaires.
Le code devient alors:
for (j=1;j<=N;j++)
for (k=1;k<=n;k++)
C^{(j)}=C^{(j)}+A(1:n,k)B(k,1:n/N);
Les blocs seront alors répartis par le compilateur en général
(ou avec l'aide de directives de compilation données par l'utilisateur)
comme pour l'exemple 1.
Sur une machine distribuée, on peut écrire des algorithmes dépendant plus finement
de la topologie de communication.
Supposons ici une topologie de communication particulière: les processeurs
sont reliés (de façon logique tout au moins) comme s'ils formaient
une grille N× N de processeurs en forme de tore.
L'algorithme de Cannon qui suit permet d'effectuer au mieux le calcul
de la multiplication de deux matrices.
forall (i=0;i<=N-1;i++)
left_shift_row A(i,*) by i;
forall (j=0;j<=N-1;j++)
up_shift_column A(*,j) by j;
forall (k=1;k<=N;k++)
forall (i=0;i<=N-1;i++)
forall (j=0;j<=N-1;j++)
C_{i,j}=C_{i,j}+A_{i,j}B_{i,j};
left_shift_row A by 1;
up_shift_column B by 1;
Considérons uniquement des matrices n× n sur un tore N× N
de processeurs avec
n=kN, k pair. Alors on peut voir que
le nombre de messages envoyés en parallèle est 4N-2, le nombre de coefficients
envoyés est (n/ N)2.(4N-2) et
le nombre d'opérations flottantes en parallèle est 2n3/ N2.
7.2 Ordonnancement de tâches parallèles
Il y a plusieurs options. On peut le faire au niveau
local c'est à dire au niveau du microprocesseur (vectorialisation etc.).
On peut aussi le faire de façon plus globale et essayer de répartir les
tâches sur les processeurs.
L'ordonnancement statique est une répartition avant exécution, alors que
l'ordonnancement dynamique se fait pendant l'exécution.
Il y a plusieurs cadres dans lesquels on peut se poser le problème.
Il faut savoir si on est intéressé par un environnement
mono-application ou pas: il peut y avoir dans le cas contraire des
problèmes de modélisation de l'attente
de ressources partagées.
Il faut également savoir si l'on veut pouvoir tenir compte d'éventuelles
prémption ou pas: dans le premier cas on s'autorise à interrompre
l'exécution d'une tâche et à la redémarrer à n'importe quel
moment, ce qui complique singulièrement la tâche.
On se place pour la suite de cette section
en mono-application, non-préemptif, statique, et global.
Le modèle simplifié que nous allons utiliser est le suivant.
On part d'un graphe pour la machine cible: P={P1,···,Pm} sont les processeurs,
(Pi,j) est la matrice de connection entre les processeurs, (Si) sont
les vitesses de chacun des processeurs.
On a également
un graphe des tâches (T,<,(Di,j),(Ai),(Wj)) avec T={T1,···,
Tn} l'ensemble des tâches, < l'opérateur de précédence, Di,j le nombre
de données à transmettre de la tâche i à la tâche j, Ai le nombre
d'instructions à exécuter par la tâche i et Wi le cout de la tâche i.
En général, le problème d'ordonnancement statique est NP-complet (problème de
minimisation sous contraintes). Mais il existe des méthodes simples dans certains
cas.
7.2.1 Premier algorithme simple
Le critère que l'on choisit pour l'ordonnancement des tâches est de
minimiser le maximum des temps auxquels les processeurs
n'ont plus rien à exécuter.
Si l'on suppose que
toutes les tâches ont le même temps d'exécution,
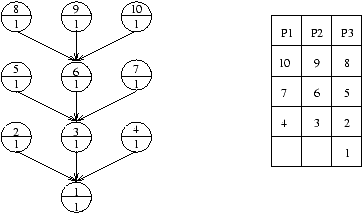
et que le graphe des tâches est un arbre fini, alors l'algorithme présenté
(l'algorithme de Hu)
dans cette section est optimal.
On appelle niveau d'un noeud x dans l'arbre des tâches le nombre maximum de noeuds
(incluant x) des chemins de x vers une feuille quelconque.
On appelle priorité d'une tâche son niveau. Ainsi,
quand un processus se libère, on lui donne la tâche avec priorité maximale.
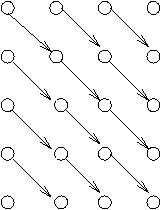
La figure 7.3 est un exemple.
Figure 7.3: Niveau des tâches
7.2.2 Deuxième algorithme
On suppose maintenant que le graphe de tâches est un graphe acyclique quelconque
mais on se restreint au cas où l'on a
m=2 processeurs.
Le but est de retrouver une notion de niveau l,
- On pose l(x)=1 pour toutes les feuilles x,
- On suppose que l'on a utilisé les niveaux 1 à j-1. Soit S l'ensemble des
tâches dont on n'a pas le niveau et dont tous les successeurs ont un niveau.
- Pour tout x de S on pose k(x)=(l(y1),···,l(yu)), la suite des
niveaux des successeurs de x écrits dans l'ordre décroissant.
- Soit x dans S avec k(x) minimal (ordre lexicographique) dans k(S).
Alors on pose l(x)=j.
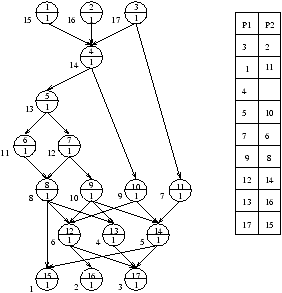
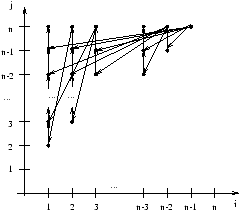
La figure 7.4 fournit un exemple d'utilisation de cet algorithme.
Figure 7.4: Exemple simple d'utilisation du deuxième algorithme d'ordonnancement
Dans la pratique,
après avoir imaginé un algorithme, il faut trouver les tâches
(ici sans boucles...),
examiner le problème du placement des tâches,
et en déduire les ``spawn'' et les ``barrier'' nécessaires.
Jusqu'à présent nous n'avons pas mis en oeuvre les communications.
Cela complique encore le problème.
Figure 7.5: Ordonnancement en présence de communications
Il existe un certain nombre d'heuristiques possibles.
On peut changer le ``grain'' de parallélisme: tâches plus grosses, moins
de délai à cause des communications mais moins de parallélisme.
Ou encore on peut
utiliser les méthodes précédentes mais avec une notion différente
de niveau. Enfin,
dans le cas où les communications sont très chères on peut même
en arriver à faire de la duplication de tâches!
Pour considérer les communications,
on inclut les ``tâches de communication'', donc le niveau de x est le maximum des
temps d'exécution et de communication des chemins partant de x.
Le problème est que le cout de communication dépend de l'allocation des tâches en
général! Un algorithme possible est le suivant:
on commence par choisir un ordonnancement, puis on calcule
les niveaux en incluant les couts de communication. Enfin on
itère ce procédé jusquà obtenir une solution stable.
Ensuite on doit faire une analyse de performances plus fine. Eventuellement on peut
remplacer
des pvm_recv bloquants par des pvm_nrecv non-bloquants et améliorer ainsi
le recouvrement calculs/communications.
7.2.3 Ordonnancement de boucles
On considère plus spécifiquement ce qui se passe dans des boucles imbriquées
telles que,
for (i1=l1;i1<=m1;i1++)
for (i2=l2;i2<=m2;i2++)
etc.
for (ik=lk;ik<=mk;ik++)
Corps;
On appelle espace d'itération l'ensemble de valeurs que peut prendre
le vecteur (i1,i2,···,ik) (sous-espace de INk).
Parallélisation par analyse de dépendance
La littérature distingue les notions de dépendance
de flot (df),
anti (da),
et de sortie (do). On a dépendance de flot entre une ligne
de code l et une autre m, accessible depuis l,
si l assigne une valeur à une variable
qui est lue en m. On a parcontre dépendance anti si on lit en l une variable
qui est affectée en m. Enfin, la dépendance de sortie est le cas où
on lit en l et en m la même variable. La notion importante pour la
parallélisation est celle de dépendance de flot: on ne peut exécuter en
parallèle sans synchronisation deux lignes ou deux tâches avec une dépendance
de flot.
Les graphes de dépendances sont des graphes indiquant la dépendance d'une itération
(i1,···,ik) à une itération (j1,···,jk).
Par exemple, pour le code suivant, on a le graphe de dépendance
de la figure 7.6:
S1: x=y+1;
for (i=2;i<=30;i++)
{
S2: C[i]=x+B[i];
S3: A[i]=C[i-1]+z;
S4: C[i+1]=B[i]*A[i];
for (j=2;j<=50;j++)
{
S5: F[i,j]=F[i,j-1]+x;
}
}
S6: z=y+3;
Figure 7.6: Graphe de dépendance
Ils permettent de trouver les calculs suffisament indépendants pour être
parallélisés.
Par exemple on considère le code suivant qui a pour graphe de dépendance
le graphe de la figure 7.7:
for (i=1;i<=5;i++)
for (j=1;j<=4;j++)
X[i+1,j+1]=X[i,j]+Y[i,j];
Figure 7.7: Un autre graphe de dépendance
Dans le cas où, comme dans ce code,
le corps des boucles est composé de calculs sur des tableaux
(c'est ce qui implique les dépendances),
et l'accès à un indice de tableau dans les boucles se fait
par un calcul linéaire sur le vecteur d'itération (i1,···,ik)
alors le calcul de dépendance peut se faire en résolvant des systèmes
d'équations Diophantiennes.
C'est le cas typiquement de schémas de calcul numérique.
Prenons l'exemple suivant:
for (i=1;i<=101;i++)
{
S1: A[2*i]=...;
S2: ...=A[3*i+198];
}
Pour savoir si on peut avoir dépendance de flot entre S1 et S2, il
faut trouver des solutions à
2x=3y+198
avec 1 £ x,y £ 101.
La solution générale est x=3t+396, y=2t+198.
D'où -131 £ t £ -99
et -98 £ t £ -49, ce qui est impossible.
Donc il n'y a pas de dépendance
et les boucles sur S1 et sur S2 peuvent être faites sur deux processeurs
différents.
7.2.4 Optimisation de la parallélisation
L'optimisation par transformation du code source peut se faire étant donnée
l'analyse de dépendance précédente. Pour cela il y a un certain nombre
de transformations élémentaires que l'on peut effectuer, et que certains
compilateurs parallélisants peuvent faire de façon automatique.
Fusion de boucles
Par exemple:
forall (i=1;i<=N;i++)
D[i]=E[i]+F[i];
forall (j=1;j<=N;j++)
E[j]=D[j]*F[j];
devient,
forall (i=1;i<=N;i++)
{
D[i]=E[i]+F[i];
E[j]=D[j]*F[j];
}
Cela permet une vectorisation et donc une
réduction du cout des boucles parallèles.
Composition de boucles
Le code:
forall (j=1;j<=N;j++)
forall (k=1;k<=N;k++)
...
devient,
forall (i=1;i<=N*N;i++)
...
Cela permet de changer l'espace d'itérations (afin d'effectuer éventuellement
d'autres transformations).
Distribution de boucles
Le code:
for (i=1;i<=N;i++)
{ A[i+1]=B[i-1]+C[i];
B[i]=A[i]*K;
C[i]=B[i]-1; }
devient,
for (i=1;i<=N;i++)
{ A[i+1]=B[i-1]+C[i];
B[i]=A[i]*K; }
forall (i=1;i<=N;i++)
C[i]=B[i]-1;
Echange de boucles
Le code:
forall (i=2;i<=N;i++)
for (j=2;j<=M;j++)
A[i,j]=A[i,j-1]+1;
devient,
for (j=1;j<=M;j++)
A[1:N,J]=A[1:N,j-1]+1;
Division de noeud
Le code:
for (i=1;i<=N;i++)
{ A[i]=B[i]+C[i];
D[i]=A[i-1]*A[i+1]; }
devient,
for (i=1;i<=N;i++)
{ A[i]=B[i]+C[i];
temp[i]=A[i+1];
D[i]=A[i-1]*temp[i]; }
Le cycle interne de dépendance est ainsi remplacé par une anti-dépendance.
Donc après distribution de boucle, on aura:
forall (i=1;i<=N;i++)
temp[i]=A[i+1];
forall (i=1;i<=N;i++)
A[i]=B[i]+C[i];
forall (i=1;i<=N;i++)
D[i]=A[i-1]*temp[i];
Réduction de boucle
Dans le cas où le cycle interne de dépendance est de type dépendance
de flot on ne peut pas utiliser la méthode précédente mais, par exemple:
for (i=3;i<=N;i++)
{ A[i]=B[i-2]-1;
B[i]=A[i-3]*k; }
devient,
for (j=3;j<=N;j=j+2)
forall (i=j; i<=j+1; i++)
{ A[i]=B[i-2]-1;
B[i]=A[i-3]*k; }
Déroulement de boucle
Le code:
for (i=1;i<=100;i++)
A[i]=B[i+2]*C[i-1];
devient,
for (i=1;i<=99;i=i+2)
{
A[i]=B[i+2]*C[i-1];
A[i+1]=B[i+3]*C[i];
}
Rotation de boucle
Le code:
for (i=2;i<=N-1;i++)
for (j=2;j<=N-1;j++)
A[i,j]=(A[i+1,j]+A[i-1,j]+A[i,j+1]+A[i,j-1])/4;
Il y a un front d'onde, cela devient,
forall (i=2;i<=N-1;i++)
for (j=i+2;j<=i+N-1;j++)
A[i,j-1]=(A[i+1,j-i]+A[i-1,j-i]+A[i,j+1-i]+A[i,j-1-i])/4;
7.3 Un exemple complet de parallélisation de code
Ce qui va nous intéresser ici est la phase
de remontée qui est la dernière étape de la résolution du
système linéaire (après une triangularisation de Gauss ou une décomposition
de Cholesky).
Soit donc à résoudre le système triangulaire supérieur
Ux=b
avec,
| U= |
æ
ç
ç
ç
è |
| U1,1 |
U1,2 |
U1,3 |
··· |
U1,n |
| 0 |
U2,2 |
U2,3 |
··· |
U2,n |
| |
|
|
··· |
|
| 0 |
0 |
··· |
0 |
Un,n |
|
ö
÷
÷
÷
ø |
et Ui,i ¹ 0 pour tout 1 £ i £ n.
On procède par ``remontée'' c'est à dire que l'on
calcule successivement,
pour i=n-1,n-2,···,1.
Le code séquentiel correspondant est alors:
x[n]=b[n]/U[n,n];
for (i=n-1;i>=1;i--)
{
x[i]=0;
for (j=i+1;j<=n;j++)
L: x[i]=x[i]+U[i,j]*x[j];
x[i]=(b[i]-x[i])/U[i,i];
}
On a représenté dans la figure 7.8 le graphe de
dépendances des tâches pour n-1 processeurs en mémoire partagée.
Figure 7.8: Graphe de dépendance
pour n-1 processeurs en mémoire partagée
Il s'agit essentiellement de dépendances de flot. On a aussi des anti-dépendances
(qui n'ont absolument aucune importance en ce qui concerne la parallélisation
et que l'on n'a donc pas représenté sur la figure)
des itérations (i,j) vers (i-1,j) (et ainsi de suite par transitivité).
7.3.1 Amélioration en mémoire partagée
En faisant une rotation et une distribution de boucles et en rajoutant
des étiquettes pour faciliter la discussion sur la complexité on obtient
le code suivant:
H': forall (i=1;i<=n-1;i++)
x[i]=b[i];
T': x[n]=b[n]/U[n][n];
H: for (t=1;t<=n-1;t++)
forall (i=1;i<=n-t;i++)
L: x[i]=x[i]-x[n-t+1]*U[i][n-t+1];
T: x[n-t]=x[n-t]/U[n-t][n-t];
Si on ne regarde que la partie H du code (la seule vraiment importante
asymptotiquement), on a
un coût de 2 pour L,
et un coût de 1 pour rapatrier x[n-t+1]
Tous ces calculs se recouvrent dans le forall. Ils sont donc à sommer pour
chaque boucle sur t, tout comme le coût égal à un de
T, donc un coût de 4(n-1) pour H. A cela, il faut ajouter
le temps pour H' égal à un et encore
un pour T'. Donc un coût total de 4n-2.
Pour le code séquentiel, si on compte l'affectation à zéro comme
une opération élémentaire de coût unitaire, le coût total est,
1+3(n-1)+2(1+2+···+n-1) = (n-1)(n+3)+1
Le ratio d'accélération est donc d'ordre n/ 4 asymptotiquement.
7.3.2 Passage de messages
On rend explicite les communications entre les processeurs
qui gèrent chacun une partie du tableau U. De fait, on suppose
que l'on a n processeurs P1,···,Pn
et que l'on répartit les tableaux de la façon suivante,
| P1 |
P2 |
P3 |
··· |
Pn-1 |
Pn |
| b[1] |
b[2] |
b[3] |
··· |
b[n-1] |
b[n] |
| U[1,n] |
U[2,n] |
U[3,n] |
··· |
U[n-1,n] |
U[n,n] |
| U[1,n-1] |
U[2,n-1] |
U[3,n-1] |
··· |
U[n-1,n-1] |
|
| ··· |
··· |
··· |
··· |
|
|
| U[1,1] |
|
|
|
|
|
Le code PVM correspondant est comme suit.
Pn est le maître qui a pour code:
T(n,1): x[n]=b[n]/U[n][n];
/* tids est le tableau d'identificateurs */
/* esclave est le code executable des autres processus */
pvm_spawn("esclave",NULL,PvmTaskDefault,"",n-1,tids);
for (i=1;i<=n-1;i++)
{
pvm_initsend(PvmDataDefault);
pvm_pkint(&i,1,1);
/* on envoie la colonne i */
pvm_pkfloat(U[i],n,1);
pvm_pkfloat(&(b[i]),1,1);
pvm_pkfloat(&(x[n]),1,1);
pvm_pkint(tids,n-1,1);
/* TAG est le filtre d'envoi d'initialisation */
pvm_send(tids[i-1],TAG);
}
T(n,2): for (i=1;i<=n-1;i++)
{
/* RES est le filtre d'envoi des resultats */
pvm_recv(tids[i-1],RES);
pvm_upkfloat(&(x[i]),1,1);
}
/* le resultat est dans le vecteur x[] */
Les esclaves Pi (1 £ i £ n-1) ont tous le même code
``esclave'' suivant (avec des annotations pour simplifier la
décomposition en tâches):
T(i,1): pvm_recv(pvm_parent(),TAG);
pvm_upkint(&i,1,1);
pvm_upkfloat(U[i],n,1);
pvm_upkfloat(&(b[i]),1,1);
pvm_upkfloat(&(x[n]),1,1);
pvm_upkint(tids,n-1,1);
x[i]=U[i][n]*x[n];
for (j=n-1;j>i;j--)
{
T(i,2,j): /* INTER est le filtre de communication entre esclaves */
pvm_recv(tids[j],INTER);
pvm_upkfloat(&(x[j]),1,1);
x[i]=x[i]+U[i][j]*x[j];
}
T(i,3): x[i]=(b[i]-x[i])/U[i][i];
for (j=1;j<i;j++)
{
pvm_initsend(PvmDataDefault);
pvm_pkfloat(&(x[i]),1,1);
pvm_send(tid[j],INTER);
}
T(i,4): pvm_initsend(PvmDataDefault);
pvm_pkfloat(&(x[i]),1,1);
pvm_send(pvm_myparent(),RES);
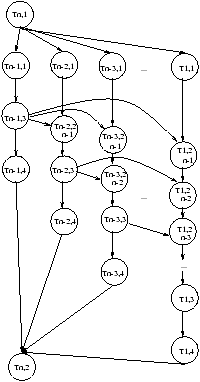
Le graphe de dépendance est décrit dans la figure 7.9.
Figure 7.9: Graphe de dépendance pour n processeurs distribués
En supposant que le coût de l'envoi et le coût
de la réception (hors attente) est égal
à la taille des données envoyées multipliée par a (0 £ a £ 1)
et
ne dépend ni du processeur ni de l'historique des calculs.
En supposant également
a très petit et n pas trop élevé, on a pour chaque processus
des temps qui se recouvrent comme suit:
| Pn |
Pn-1 |
··· |
P1 |
|
|
-- |
··· |
-- |
| -- |
|
··· |
|
| -- |
|
··· |
-- |
| -- |
|
··· |
|
|
|
-- |
··· |
-- |
| ··· |
··· |
··· |
··· |
| a |
-- |
··· |
-- |
Donc la première ligne du tableau correspond à un coût global de
1+2a(n-1)(n+1), puis les deux premières à 2+2a(n+1),
puis les quatre premières: 6+a(2n(n+1)+n-1), puis si on somme les
lignes deux par deux, on rajoute 2+a(n-i) (3 £ i £ n) et
a+2. On termine enfin par ajouter a (pour T1,4) et
a (pour Tn,2). Donc le coût global est,
6+4(n-2)+a(2n(n+1)+(n-1)+(n-2)+···+1)+2a
donc le coût est 4n-2+a/ 2(5n2+3n+4).
Le coût est donc exactement celui du programme SIMD plus le coût
explicite des communications. On aurait pu mieux ordonnancer les envois
et gagner un peu sur ce temps supplémentaire, mais il serait resté en
a n2. C'est le coût des compactage et décompactage des données
tel qu'il est programmé ici.
Une autre solution aurait été de
répartir les lignes de U
sur les processeurs modulo p (donc les lignes U[1,*], U[1+p,*],
···, U[1+(k-1)*p,*] sur P1 etc.).
Le nouveau code agit alors comme si on avait recopié p fois le code du maître
et p fois le code des esclaves. Cela ne change rien à la complexité
de l'algorithme, si on a bien fait attention à la gestion des ``broadcast''
vers les processus de numéro plus élevés.
Encore une autre solution
serait de mettre des lignes adjacentes de U sur chacun des processeurs, c'est
à dire de découper U en bandes horizontales.
On suppose que l'on fait gérer les lignes j, 1 £ ki £ j £ li £ n
au processeur i (1 £ i £ n), et que i' > i implique ki' > li',
plus ki+1=li+1, k1=1, lp=n.
Le code PVM correspondant est comme suit.
On a le squelette suivant, pour le maître (Pp):
/* resolution pour les inconnues x[k[p]] a x[n] */
T(p,1):...
/* tids est le tableau d'identificateurs */
/* esclave est le code executable des autres processus */
pvm_spawn("esclave",NULL,PvmTaskDefault,"",n-1,tids);
for (i=1;i<=n-1;i++)
{
pvm_initsend(PvmDataDefault);
pvm_pkint(&i,1,1);
/* on envoie la colonne i */
pvm_pkfloat(U[i],n,1);
pvm_pkfloat(&(b[i]),1,1);
pvm_pkfloat(&(x[k[p]]),n-k[p]+1,1);
/* on envoie k_i, l_i mis dans un tableau k[] et l[] */
pvm_pkint(k,p,1);
pvm_pkint(l,p,1);
pvm_pkint(tids,n-1,1);
/* TAG est le filtre d'envoi d'initialisation */
pvm_send(tids[i-1],TAG);
}
T(n,2): for (i=1;i<=n-1;i++)
{
/* RES est le filtre d'envoi des resultats */
pvm_recv(tids[i-1],RES);
pvm_upkfloat(&(x[k[i]]),l[i]-k[i]+1,1);
}
/* le resultat est dans le vecteur x[] */
Les esclaves Pi (1 £ i £ p-1) ont tous le même code
``esclave'' suivant:
T(i,1): pvm_recv(pvm_parent(),TAG);
pvm_upkint(&i,1,1);
pvm_upkfloat(U[i],n,1);
pvm_upkfloat(&(b[i]),1,1);
pvm_upkfloat(&(x[n]),1,1);
pvm_upkint(k,p,1);
pvm_upkint(l,p,1);
pvm_upkint(tids,n-1,1);
/* initialisation des variables x[k[i]] a x[l[i]] */
...
for (j=p-1;j>i;j--)
{
T(i,2,j): /* INTER est le filtre de communication entre esclaves */
pvm_recv(tids[j],INTER);
pvm_upkfloat(&(x[k[j]]),l[j]-k[j]+1,1);
...
/* resolution ... */
}
T(i,3): for (j=1;j<i;j++)
{
pvm_initsend(PvmDataDefault);
pvm_pkfloat(&(x[k[i]]),l[i]-k[i]+1,1);
pvm_send(tid[j],INTER);
}
T(i,4): pvm_initsend(PvmDataDefault);
pvm_pkfloat(&(x[k[i]]),l[i]-k[i]+1,1);
pvm_send(pvm_myparent(),RES);$i' > i$
Avec des processeurs d'égale puissance, le mieux est de découper
en domaines avec un même nombre de lignes, donc ki=1+k(i-1) et li=ki,
Une meilleure solution consiste à envoyer x[k[i]] sitôt calculé,
aux esclaves Pi', i' > i, puis x[k[i]+1] jusqu'à x[l[i]] sitôt
calculés. Cela permet de recouvrir bien mieux les calculs et les communications
que dans la solution
précédente.
- 1
- On remarquera à ce propos que l'on a une bordure de points
que l'on ne calcule pas, mais qui est présente pour forcer les conditions
aux limites de façon simple.
- 2
- En fait, il s'agit d'une
opération de réduction, qui existe sous PVM par exemple, et qui est
implémentée par un algorithme diviser-pour-régner, prenant un temps de
log2 p.
- 3
- Ou
encore en utilisant les ``handler'' de PVM3.4, voir chapitre B,
permettant d'exécuter une fonction (définie par le programmeur) au moment de la
réception d'un message avec le bon TAG.