Chapter 3 Equation de Laplace en dimension 1
Ce chapitre et le suivant présentent succinctement des méthodes
de décomposition de domaine.
La résolution numérique des équations aux dérivées partielles
intervient dans de nombreux domaines scientifiques et
industrielles: météorologie, aéronautique, électronique,
télécommunications, mathématiques financières, automobile,
environnement, ....
Une des principales limitations de la précision des calculs
vient de la place en mémoire vive exigée par les simulations de
dispositifs complets. En effet, celle-ci ne varie pas linéairement
avec la taille du domaine de calcul.
L'emploi de calculateurs parallèles permet dans une large
mesure de s'affranchir de cette limite. La place mémoire
disponible dépend linéairement du nombre de processeurs du
calculateur. Les données de la simulation sont réparties
sur les processeurs.
L'accès d'un processeur à sa zone mémoire est
beaucoup plus rapide que l'accès aux mémoires des autres
processeurs. Ceci oblige à repenser les
algorithmes conçus pour les calculateurs "classiques" et à en
proposer de nouveaux qui soient adaptés aux nouvelles architectures.
Les méthodes de décomposition de domaine présentées dans ce
chapitre et le suivant en sont des exemples. On considère un
problème posé sur un (grand) domaine de calcul. Ce domaine est
décomposé en (petits) sous-domaines. Chaque sous-domaine est
attribué à un processeur. Les problèmes sont résolus en parallèle
sur chaque sous-domaine. Pour que les solutions locales ainsi
calculées correspondent à la solution du problème global, il est
nécessaire d'imposer un raccord continu des solutions locales.
Ceci se fait à l'aide d'une méthode itérative.
Nous présentons ici quelques algorithmes de
méthodes de décomposition de domaine dans le cadre de l'équation de
Laplace en dimension 1 d'espace (ce chapitre) et en dimension 2
(chapitre suivant). La méthode est d'abord présentée au niveau
continu puis sur le problème discrétisé. Dans chaque cas, on
considère tout d'abord des conditions de raccord de Dirichlet
(continuité de la solution) puis de Robin (raccord d'une combinaison
linéaire du flux et de la valeur de la solution). L'intérêt de
dernier choix est développé. Une décomposition en deux
sous-domaines seulement est considérée.
Ces méthodes sont en
fait très générales et s'appliquent à des équations plus complexes
et à des géométries plus générales que celles présentées ici. Il
est aussi important ce signaler que ces méthodes sont aussi très
intéressantes pour des ordinateurs monoprocesseurs. Dans ce cas,
le processeur traite successivement les sous-domaines. Le gain en
place mémoire vient du fait que le coût d'une simulation numérique
n'est pas linéaire par rapport à la taille du domaine de calcul.
3.1 Aspect mathématique
3.1.1 Solutions explicites
Nous considérons l'équation de Laplace
où u est une fonction scalaire de la variable d'espace
xÎ [0,L] avec différents jeux de conditions aux limites:
ou bien
|
u(0)=g0 et
( |
|
+a u)(L)=gL,
(3.3) |
a est une constante positive ou nulle et g0, gL
sont des nombres réels. Nous désignerons par P1 le problème (3.1)-(3.2)
et par P2 le problème
(3.1)-(3.3).
Etude du problème P1
L'équation (3.1) est une équation différentielle
ordinaire en x dont la solution générale est
u(x)=a+bx, a, bÎIR.
Les conditions aux limites (3.2) sont satisfaites si et
seulement si
a et b vérifient
dont l'unique solution est
Le problème P1 admet donc aussi une solution unique:
|
u(x)=g0 + |
|
x= gL+ |
|
(x-L).
(3.5) |
Etude du problème P2
L'équation (3.1) est une équation différentielle
ordinaire en x dont la solution générale est
u(x)=a+bx, a, bÎIR.
Les conditions aux limites (3.3) sont satisfaites si et
seulement si
a et b vérifient
|
|
ì
í
î |
| a = g0 |
| b+ a(a+ b L) = gL.
|
|
(3.6) |
dont l'unique solution est
Le problème P2 admet donc aussi une solution unique
Remarque 3.1.1 L'équation de Laplace avec un second membre f dans
(3.1) et les conditions aux limites (3.2)
ou (3.3) se ramène au problème P1 ou P2: on introduit
la fonction w(x)=-ò0x (ò0s f(t) dt) ds telle que
-wxx=f. Par linéarité de l'équation de
Laplace, on peut chercher la solution sous la
forme v+w où v satisfait l'équation
(3.1) avec les second membres des
conditions aux limites (3.2) ou
(3.3) modifiés.
3.2 Méthodes de décomposition de domaine - Cas continu
Nous considérons l'équation
unidimensionnelle
où u et f sont des fonctions scalaires de la variable
d'espace
xÎ [0,L] avec des conditions aux limites de Dirichlet:
où g0, gLÎ IR.
Le segment W
=[0,L] est décomposé en deux sous-domaines W1=[0,L1]
et W2=[l2,L],
0<l2£ L1<L. Nous désignerons par P le
problème défini par
(3.7)-(3.8). Nous allons
réécrire P de deux manières différentes sous la
forme de deux problèmes couplés posés dans les
sous-domaines W1 et W2. Puis, nous
étudierons une méthode itérative de résolution
de ces systèmes couplés adaptée aux architectures
parallèles.
On désigne par u1 la restriction de u au domaine
W1 et par u2 sa restriction au domaine W2.
Le couple
(u1,u2) vérifie
D'après (3.9), la forme générale de u1 est
donnée par
et d'après (3.10), celle de u2 est
On voit que les équations
(3.9)-(3.10) ne suffisent pas à
déterminer de manière unique le couple
(u1,u2). Dans les paragraphes qui suivent, nous ajoutons
des conditions de raccord aux interfaces (dites aussi
conditions d'interface)
x=L1 et
x=l2 pour que le couple (u1,u2) soit déterminé de
manière unique et soit égal aux restrictions de u aux
sous-domaines
W1 et W2. Pour
chaque jeu de conditions d'interfaces, on propose une méthode
itérative de résolution adaptée aux
architectures parallèles.
3.2.1 Reformulation avec des conditions de
Dirichlet - Problème P'
Nous ajoutons des conditions de
raccord de type Dirichlet:
et
Nous désignerons par P' le
problème
(3.9)-(3.10)-(3.11)-(3.12).
Nous allons montrer que ce problème admet un couple solution
unique (u1,u2) si et seulement si les sous-domaines se
recouvrent (L1>l2).
Existence
La solution u du problème P
((3.7)-(3.8)) étant
continuement dérivable, le couple (u1,u2), où
u1=u|W1 et
u2=u|W2, est solution du problème P'.
Remarquons que s'il y a unicité, la solution de P' est
la restriction de u aux sous-domaines.
Unicité
Par linéarité des équations, il suffit de considérer les
équations homogènes
g0=gL=f=0. D'après (3.9) et
(3.10), on a
u1(x)= b1 x
et
u2(x)=b2 (x-L).
où b1, b2Î IR. Les conditions de raccord
(3.11)-(3.12) deviennent:
b1 L1=b2 (L1-L)
et
b2 (l2-L) = b1 l2.
Il s'agit d'un système en b1, b2:
|
|
ì
í
î |
| L1 b1 - (L1-L) b2=0 |
| -b1 l2 + b2 (l2-L) = 0.
|
|
(3.11) |
Le déterminant de (3.13) vaut L(l2-L1).
Il est
non nul ssi les sous-domaines se recouvrent, l2<L1,
(rappelons que l'on a déjà
l2£ L1). Alors, on a b1=b2=0,
u1(x)=0 et
u2(x)=0. Ceci prouve l'unicité.
Dans le cas où les sous-domaines sont adjacents (l2=L1), le
déterminant de (3.13) s'annule, et le système
linéaire (3.13) admet une infinité de solutions
b1=l2-L/ l2 b2, b2=b2. Il en est alors de
même du problème P' qui admet une infinité à un paramètre de
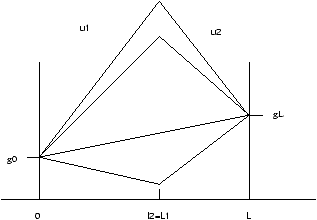
solutions. Ces solutions sont affines dans chacun des sous-domaines
et se raccordent en L1=l2 (voir
Figure 3.1).
Figure 3.1: Solutions multiples dans le cas sans recouvrement l2=L1.
On a ainsi montré le
Lemme 3.2.1 Le problème P' (Eqs.
(3.9)-(3.10)-(3.11)-(3.12))
admet une unique solution ssi les sous-domaines se
recouvrent. Dans ce cas, la solution
(u1,u2) de P' est composée des restrictions, aux
sous-domaines, de la solution u du problème P (i.e. u1=u
sur W1 et
u2=u sur W2).
3.2.2 Algorithme parallèle de résolution
du problème P' (Algorithme de Schwarz)
Nous considérons une méthode itérative
de résolution du problème P'. On part de u10 et u20
quelconques et on pose
|
|
|
ì
ï
ï
í
ï
ï
î |
|
|
| u1n+1(0)=g0 |
| u1n+1(L1)=u2n(L1)
|
|
|
|
|
ì
ï
ï
í
ï
ï
î |
|
|
| u2n+1(L)=gL |
| u2n+1(l2)=u1n(l2)
|
|
|
|
Les problèmes définissant l'algorithme sont du type P1 et
sont donc bien posés.
Remarque 3.2.1 L'algorithme de Schwarz est bien adapté au calcul
parallèle. On peut affecter un processeur à chaque
sous-domaine. Les résolutions des problèmes de
Laplace dans les sous-domaines sont indépendantes
et peuvent être effectuées en parallèle. Une fois
ce calcul terminé, chaque sous-domaine envoie à
son voisin la valeur dont le voisin a besoin pour
mettre à jour le second membre de son problème de
Dirichlet (i.e. les valeurs courantes de
u1(l2) et
u2(L1)). La quantité de données à transmettre
est très petite par rapport à la quantité de
données à traiter par chaque sous-domaine. Il
s'agit d'un algorithme à gros grain.
La traduction en PVM de cet algorithme est très simple. On a tout d'abord
un programme maître qui est chargé de lancer un esclave par sous-domaine:
#include <stdio.h>
#include "pvm3.h"
/* Tag des messages d'initialisation */
#define INIT 0
/* Nombre de sous-domaines */
#define NB_DOMAINES 2
/* Condition aux limites gauche */
double g0;
/* Condition aux limites droite */
double gL;
/* tids des esclaves */
int esclaves[NB_DOMAINES];
int n;
double d;
int main()
{
/* par exemple... */
g0=1;
gL=2;
/* on se raccroche au demon pvmd */
if (pvm_mytid() < 0)
{
printf("Impossible de lancer le maitre\n");
exit(1);
}
/* on cree les processus esclaves */
n=pvm_spawn("esclave",NULL,PvmTaskDefault,NULL,NB_DOMAINES,
&esclaves[0]);
if (n < NB_DOMAINES)
{
printf("Impossible de lancer tous les esclaves\n");
pvm_exit();
exit(1);
}
/* on envoie les noms des voisins et les
conditions aux limites par sous-domaine */
/* d'abord le bord gauche du domaine total */
pvm_initsend(PvmDataDefault);
n=-1;
pvm_pkint(&n,1,1);
pvm_pkint(&esclaves[1],1,1);
pvm_pkdouble(&g0,1,1);
d=0;
pvm_pkdouble(&d,1,1);
pvm_send(esclaves[0],INIT);
/* ensuite l'interieur du domaine total */
for (i=1;i<NB_DOMAINES-1;i++)
{
pvm_initsend(PvmDataDefault);
pvm_pkint(&esclaves[i-1],1,1);
pvm_pkint(&esclaves[i+1],1,1);
d=0;
pvm_pkdouble(&d,1,1);
pvm_pkdouble(&d,1,1);
pvm_send(esclaves[i],INIT);
}
/* enfin le bord droit du domaine total */
pvm_initsend(PvmDataDefault);
pvm_pkint(&esclaves[NB_DOMAINES-2],1,1);
n=-1;
pvm_pkint(&n,1,1);
d=0;
pvm_pkdouble(&d,1,1);
pvm_pkdouble(&gL,1,1);
pvm_send(esclaves[NB_DOMAINES-1],1,1);
/* on termine */
pvm_exit();
exit(0);
}
Chaque esclave ``esclave.c'' a pour structure:
#include <stdio.h>
#include "pvm3.h"
/* Tag des messages d'initialisation */
#define INIT 0
/* Tag des messages inter-esclaves */
#define INTER 1
/* Nombre d'iterations pour Schwarz */
#define ITER 1000
/* echantillonage de la solution u
(voir discretisation )*/
#define N 100
/* tid des voisins, egal a -1 si n'existe pas */
int voisin_gauche, voisin_droit;
/* solution u discretisee a une etape donnee */
double u[N];
int i;
void resolution()
/* resoud le probleme dans le sous-domaine */
/* a partir des conditions aux limites u[0], u[N-1] */
{
...
}
int main()
{
/* reception des parametres */
pvm_recv(-1,INIT);
pvm_upkint(&voisin_gauche,1,1);
pvm_upkint(&voisin_droit,1,1);
pvm_upkdouble(&u[0],1,1);
pvm_upkdouble(&u[N-1],1,1);
/* Algorithme de Schwarz */
for (i=0;i<ITER;i++)
{
/* calcul de la solution dans le sous-domaine */
resolution();
if (voisin_gauche>0)
/* echanges avec le voisin gauche */
{
pvm_initsend(PvmDataDefault);
pvm_pkdouble(&u[0],1,1);
pvm_send(voisin_gauche,INTER);
}
if (voisin_droit>0)
/* echange avec le voisin droit */
{
pvm_pkdouble(&u[N-1],1,1);
pvm_send(voisin_droit,INTER);
}
if (voisin_gauche>0)
/* reception du voisin gauche */
{
pvm_recv(voisin_gauche,INTER);
pvm_upkdouble(&u[0],1,1);
}
if (voisin_droit>0)
/* reception du voisin droit */
{
pvm_recv(voisin_droit,INTER);
pvm_upkdouble(&u[N],1,1);
}
}
/* affichage des resultats */
...
/* fin */
pvm_exit();
exit(0);
}
Remarques:
On aurait pu passer les paramètres aux esclaves directement
à leur création. Dans la pratique également, le maître serait
chargé d'attendre la fin de chaque esclave et de réceptionner leurs
calculs pour affichage ou dépouillement.
Il faut aussi remarquer que pvm_send étant non-bloquant
alors que pvm_recv est bloquant, il vaut mieux que chaque esclave
envoie ses valeurs limites, avant d'attendre les informations de ses voisins
(le contraire produirait un interblocage).
Dans la pratique enfin, le nombre d'itérations ne serait sans doute
pas fixé; le test d'arrêt serait plutôt exprimé par une condition
de convergence.
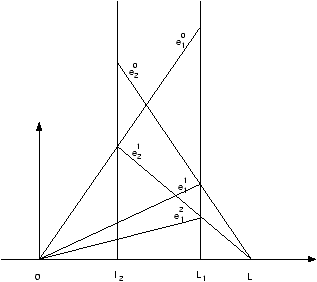
Figure 3.2: Evolution de l'erreur dans l'algorithme de Schwarz.
Remarque 3.2.2 Une solution stationnaire de
l'algorithme est solution du problème P'. Ceci prouve que si
l'algorithme converge, il converge vers
l'unique solution (quand les sous-domaines se chevauchent)
de P' qui est la restriction aux sous-domaines
W1 et
W2 de la solution u du problème P. L'algorithme de
Schwarz (3.14)-(3.15) sera
donc une méthode itérative de résolution du problème P.
Pour étudier la convergence, on pose
e1n=u1n-u1 et
e2n=u2n-u2 où (u1,u2) est la solution du
problème P'. Par linéarité des équations, l'erreur
(e1n,e2n) vérifie
|
|
|
ì
ï
ï
í
ï
ï
î |
|
|
| e1n+1(0)=0 |
| e1n+1(L1)=e2n(L1)
|
|
|
|
|
ì
ï
ï
í
ï
ï
î |
|
|
| e2n+1(L)=0 |
| e2n+1(l2)=e1n(l2)
|
|
|
|
On a ainsi, pour n³ 2, e1n=g1n x et
e2n=g2n (x-L). Les conditions de Dirichlet en x=L1
et x=l2 donnent
|
g1n+1L1=g2n (L1 -L) |
| g2n+1(l2-L)=g1n l2.
|
On a donc
| g1n+1= |
|
g2n
= |
|
|
|
g1n-1
= |
|
|
|
g1n-1º b
g1n-1.
|
La relation est aussi valable pour g2n+1. Comme
l2£ L1, le terme
b est toujours positif et on a: b<1
l2<L1. Pour l2=L1, on a
b=1 et l'algorithme stagne. On a prouvé le
Théorème 3.2.2 L'algorithme de Schwarz
(3.14)-(3.15) converge si et
seulement si les sous-domaines se recouvrent (l2<L1).
Remarque 3.2.3 L'absence de convergence dans le cas sans recouvrement est en
accord avec le
fait que le problème P' est alors mal posé.
Remarque 3.2.4 Pour un petit recouvrement, L1=l2+e,
e « 1, b dépend des pourcentages de
recouvrement
Plus le recouvrement est faible, plus la convergence est
lente.
Remarque 3.2.5 La figure 3.2 donne une interprétation
géométrique de la convergence.
3.2.3 Reformulation avec des conditions de Robin -
Problème P''
Pour fermer le système d'équations
(3.9)-(3.10), nous ajoutons des
conditions de raccord de type Robin:
|
( |
|
+a u1)(L1)=
(- |
|
+a u2)(L1)
(3.12) |
et
|
( |
|
+a u2)(l2)=
(- |
|
+a u1)(l2)
(3.13) |
où a est une constante strictement positive, n1 (resp.
n2) désigne la normale extérieure au domaine W1 (resp.
W2). Les signes - devant les dérivées normales
viennent du fait que n2=-n1. Nous désignerons par
P'' le problème
(3.9)-(3.18)-
(3.10)-(3.19). Nous allons
montrer que ce problème admet un couple solution
unique (u1,u2) avec ou sans recouvrement des
sous-domaines.
Existence
La solution u du
problème P étant continuement dérivable, le
couple (u1,u2), où u1=u|W1 et
u2=u|W2, est solution du problème P''. Remarquons
que s'il y unicité la solution de P'' est la
restriction de u aux sous-domaines.
Unicité
Par linéarité des équations, il suffit de considérer le
cas homogène f=g0=gL=0. D'après (3.9) et
(3.10), on a
u1(x)= b1 x
et
u2(x)=b2 (x-L).
où b1, b2Î IR. Les conditions de raccord
(3.18)-(3.19) deviennent:
b1+a b1 L1=b2+a b2(L1-L)
et
-b2+a b2(l2-L) =-b1+a b1 l2
Il s'agit d'un système en b1, b2:
|
|
ì
í
î |
| (1+a L1)b1 -(1-a(L-L1))b2=0 |
| (-1+a l2)b1 + (1+a(L-l2))b2 = 0.
|
|
(3.14) |
Le déterminant de (3.20) vaut a
L(2+a(L1-l2)) et est strictement positif. Le système
(3.20) admet comme unique solution la
solution nulle. Il en est alors de même du problème P''.
On a
ainsi montré le
Lemme 3.2.3 Le problème P'' (Eqs.
(3.9)-(3.18)-(3.10)-(3.19))
admet une unique solution. La
solution
(u1,u2) de P'' est composée des restrictions, aux
sous-domaines, de la solution u du problème P (i.e. u1=u
sur W1 et
u2=u sur W2).
Remarque 3.2.6 Il est important de noter que le problème P'', contrairement au
problème P', admet une solution unique même quand les
sous-domaines ne se recouvrent pas.
3.2.4 Algorithme parallèle de résolution
du problème P''
Nous considérons une méthode
itérative de résolution du problème P''. On part
de u10 et u20 quelconques et on pose
|
|
|
ì
ï
ï
ï
í
ï
ï
ï
î |
|
|
| u1n+1(0)=g0 |
| ( |
|
+a u1n+1)(L1)=(- |
|
+a u2n)(L1)
|
|
|
|
|
|
ì
ï
ï
ï
í
ï
ï
ï
î |
|
|
| u2n+1(L)=gL |
| ( |
|
+a u2n+1)(l2)=(- |
|
+a u1n)(l2)
|
|
|
|
|
Les problèmes aux limites définissant l'algorithme sont du
type P2 et donc bien posés.
Remarque 3.2.7 Une solution stationnaire de
l'algorithme est solution du problème P''. Ceci prouve que si
l'algorithme converge (voir plus loin), il converge vers
l'unique solution de P'' qui est la restriction aux
sous-domaines
W1 et
W2 de la solution u du problème P. L'algorithme
(3.21)-(3.22) sera donc
une méthode itérative de résolution du problème P.
Pour étudier la convergence, on pose e1n=u1n-u1 et
e2n=u2n-u2 où (u1,u2) est la solution du
problème P''. L'erreur (e1n,e2n) vérifie par linéarité
des équations
|
|
|
ì
ï
ï
ï
í
ï
ï
ï
î |
|
|
| e1n+1(0)=0 |
| ( |
|
+a e1n+1)(L1)=(- |
|
+a e2n)(L1)
|
|
|
|
|
|
ì
ï
ï
ï
í
ï
ï
ï
î |
|
|
| e2n+1(L)=0 |
| ( |
|
+a e2n+1)(l2)=(- |
|
+a e1n)(l2)
|
|
|
|
On a ainsi, pour n³ 2, e1n=g1n x et
e2n=g2n (x-L). Les conditions de Robin en x=L1
et x=l2 donnent
|
g1n+1+a g1n+1 L1
=g2n+a g2n (L1 -L) |
| -g2n+1+a g2n+1(l2-L)
=-g1n +a g1n l2.
|
On a donc
| g1n+1= |
|
g2n
= |
|
|
|
g1n-1=
b g1n-1.
|
où
La relation est aussi valable pour g2n+1.
Le paramètre a étant positif, on peut montrer qu'avec ou
sans recouvrement des sous-domaines,
-1<b < 1.
On a ainsi prouvé le
Théorème 3.2.4 Pour a>0, l'algorithme
(3.21)-(3.22) converge.
Remarque 3.2.8 Contrairement à l'algorithme de Schwarz, le recouvrement des
sous-domaines n'est pas nécessaire pour assurer la convergence
de l'algorithme. Dans le cas sans recouvrement (l2=L1), on
a
Remarque 3.2.9 Il est possible d'annuler b et donc d'avoir une
convergence en deux itérations en choisissant a=1/l2 ou
bien a=1/(L-L1).
3.3 Aspect numérique
3.3.1 Approximations par différences finies
Nous considérons l'équation
avec les conditions aux bords
|
u(0)=g0 et
( |
|
+a u)(L)=gL,
(3.16) |
où a est une constante positive ou nulle et g0, gL
sont des nombres réels.
Nous introduisons des schémas d'approximation par différence
finie. Nous cherchons à calculer une approximation de la
solution aux points (xj)1£ j£ N définis par
xj= (j-1) D x
où N est le nombre de points de discrétisation et D
x=L/(N-1) désigne le pas de discrétisation. On note uj
l'approximation numérique de u au point xj. Pour
approcher (3.25), on utilise un schéma centré
La condition de Dirichlet dans (3.26) est approchée
par
La condition de Robin dans (3.26) peut être
approchée de plusieurs façons. Nous en
mentionnons deux.
Possibilité n01.
Cette formule correspond à une approximation de la dérivée
première en x à l'aide d'un développement de Taylor à l'ordre
1:
|
u(xN-1)=u(xN)-D x |
|
(xN)
+O(D x2).
(3.20) |
Possibilité n02.
|
|
|
- |
|
f(xN)+a
uN = gL.
(3.21) |
Cette formule correspond à une approximation de la dérivée
première en x à l'aide d'un développement de Taylor à l'ordre
2:
|
u(xN-1)=u(xN)-D x |
|
(xN)
+ |
|
(D x)2 |
|
(xN)
+O(D x3).
(3.22) |
dans lequel on a approché ¶2 u/ ¶
x2(xN)
à l'aide de l'équation (3.27) en j=N.
La possibilité (3.31) est plus précise
que la possibilité (3.29) puisqu'elle
est en
O(D x2) alors que (3.29) est
en
O(D x).
Attention! pour estimer l'ordre on réécrit (3.30)
et (3.32) sous la forme:
et
|
|
= |
|
(xN) - |
|
D x |
|
(xN)+ O(D x2)
|
respectivement.
Remarque 3.3.1 L'inversibilité des systèmes linéaires résultants de
(3.27)-(3.28)-(3.29)
ou bien de
(3.27)-(3.28)-(3.31)
et la convergence de
uj vers
u(xj) quand D x tend vers zéro sont prouvées dans le
polycopié: [LL].
3.3.2 Systèmes matriciels de discrétisation
Nous considérons les équations aux différences finies
(3.27), (3.28),
(3.29) ou (3.31).
Nous introduisons des systèmes linéaires
correspondants à ces schémas. Plusieurs choix sont
possibles pour la matrice représentant les équations
aux différences finies.
Choix n01.
On introduit le vecteur des inconnues U=(uj)1£
j£ N. On écrit sans modification les équations aux
différences finies (3.27), (3.28).
Si on discrétise la condition de Robin par
(3.29), on a
|
|
|
æ
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
è |
|
| 1 |
|
|
|
|
|
|
|
|
|
|
|
| |
·
·
· |
·
·
· |
·
·
· |
|
|
| |
|
·
·
· |
·
·
· |
·
·
· |
|
| |
|
|
|
|
|
| |
|
|
|
|
|
|
ö
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
ø |
|
æ
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
è |
|
ö
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
ø |
|
|
| =
|
æ
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
è |
|
ö
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
ø |
.
|
|
Si on discrétise la condition de Robin par
(3.31), la matrice de discrétisation est
inchangée mais le second membre est différent:
|
|
|
æ
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
è |
|
| 1 |
|
|
|
|
|
|
|
|
|
|
|
| |
·
·
· |
·
·
· |
·
·
· |
|
|
| |
|
·
·
· |
·
·
· |
·
·
· |
|
| |
|
|
|
|
|
| |
|
|
|
|
|
|
ö
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
ø |
|
æ
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
è |
|
ö
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
ø |
|
|
| =
|
æ
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
è |
|
ö
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
ø |
.
|
|
Il est important de remarquer que les premières et dernières
lignes des matrices de (3.33) et
(3.34) les rendent non symétriques.
Choix n02.
On modifie la deuxième ligne des systèmes
linéaires du choix précédent en substituant
u1 par g0 dans la deuxième ligne qui s'écrit alors:
La dernière ligne de
(3.33) ou de (3.34)
est divisée par D x. Finalement, si la condition de
Robin (3.26) est discrétisée par
(3.29) on a le système matriciel
|
|
|
æ
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
è |
|
|
ö
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
ø |
|
æ
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
è |
|
ö
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
ø |
|
|
| =
|
æ
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
è |
|
ö
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
ø |
.
|
|
Si on discrétise la condition de Robin par
(3.31), la matrice de discrétisation
est inchangée mais le second membre est différent:
|
|
|
æ
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
è |
|
|
ö
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
ø |
|
æ
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
è |
|
ö
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
ø |
|
|
| =
|
æ
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
è |
|
ö
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
ø |
.
|
|
Il est important de remarquer la supériorité du choix n02,
qui conduit aux systèmes linéaires symétriques
(3.35)
et (3.36), par rapport au choix
n01 qui conduit aux systèmes non
symétriques
(3.33)
et (3.34).
3.4 Méthodes de décomposition de domaine - Cas discret
Dans ce paragraphe, nous donnons un équivalent discret des
méthodes de décomposition de domaine du cas continu traité
dans le paragraphe 3.2.
Nous considérons le système linéaire unidimensionnel issu de la
discrétisation du problème P (Eqs
(3.7)-(3.8)):
|
|
|
æ
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
è |
|
| 1 |
|
|
|
|
|
| 0 |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
·
·
· |
·
·
· |
·
·
· |
|
| |
|
|
|
|
0 |
| |
|
|
|
|
1
|
|
ö
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
ø |
|
æ
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
è |
|
ö
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
ø |
|
|
| =
|
æ
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
è |
|
ö
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
ø |
.
|
|
où (uj)1£ j£ N est un vecteur de réels qui sera
noté U. Rappelons
que les conditions de Dirichlet (3.8) sont
implicitement contenues dans les premières et dernières
lignes de (3.37). Nous désignerons par
Ph le problème (3.37).
L'ensemble des indices
N={1,2,...,N } est décomposé en deux
sous-ensembles d'indices N1={1,2,..., N1 } et
N2={N2, N2+1,...,N } où N1 et N2 sont des
entiers satisfaisants N2£ N1. Cela correspond à une
décomposition du segment [0,L] en deux sous-domaines
[0,L1] et [l2,L] où L1=(N1-1)D x et
l2=(N2-1)D x. Si N2<N1, on dira, par analogie
avec le cas continu, que les sous-domaines se recouvrent.
Nous allons réécrire Ph de deux
manières différentes sous la forme de deux problèmes
couplés posés sur les sous-ensembles d'indices
N1 et
N2. Nous considérons tout d'abord le
couplage par des conditions de Dirichlet puis par des
conditions de Robin discrétisées. Puis, nous
étudierons une méthode itérative de résolution de ces
systèmes couplés adaptée aux
architectures parallèles. Pour cela, nous suivrons un
plan parallèle celui du
§ 3.2 où le cas continu est
traité.
On désigne par U1 la restriction de U au
sous-ensemble d'indices N1 et par U2 sa
restriction à N2. Le vecteur
U1=(u1,j)jÎ N1 vérifie
|
|
A1 U1
=
|
æ
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
è |
|
ö
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
ø |
|
|
où
|
A1= |
æ
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
è |
|
|
ö
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
ø |
(3.23) |
est une matrice rectangulaire (N1-1)× N1. Le vecteur
U2=(u2,j)jÎ N2 vérifie
|
|
A2 U2
=
|
æ
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
è |
|
ö
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
ø |
.
|
|
où
|
A2= |
æ
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
è |
|
|
ö
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
ø |
(3.24) |
est une matrice rectangulaire
(N2-1)× N2.
Les systèmes linéaires
(3.38)-(3.40) sont donc
sous-déterminés. Dans les paragraphes qui suivent, nous
ajoutons des conditions de raccord aux interfaces en j=N1
et j=N2 pour que le couple (U1,U2) soit déterminé de
manière unique et soit égal aux restrictions de U aux
sous-ensembles d'indices N1 et N2. Pour
chaque jeu de conditions d'interfaces, on propose une méthode
itérative de résolution adaptée aux
architectures parallèles.
3.4.1 Reformulation avec des conditions de Dirichlet -
Problème P'h
Nous ajoutons les conditions de raccord de
type Dirichlet:
et
Nous désignerons par P'h le problème
(3.38)-(3.40)-(3.42)-(3.43)
Nous allons montrer que ce problème admet un couple solution
unique (U1,U2) si et seulement si les sous-domaines se
recouvrent (N1>N2).
Existence
On construit une solution de P'h à partir de la solution
U du système (3.37) en posant U1=(uj)jÎ
N1 et U2=(uj)jÎ N2.
Remarquons que
s'il y a unicité, la solution de P'h est la restriction
de U aux sous-ensembles d'indices N1 et N2.
Unicité
Par linéarité des équations, il suffit de considérer le
cas homogène g0=gL=f=0. Alors, d'après
(3.38) et (3.40), on a
et
où b1, b2Î IR. Les conditions de raccord
(3.42)-(3.43)
deviennent:
b1(N1-1)D x = b2(N1-N)D x
et
b2(N2-N)D x = b1(N2-1)D x.
Il s'agit d'un système en b1, b2:
|
|
ì
í
î |
| b1(N1-1)D x -b2(N1-N)D x= 0 |
| -b1(N2-1)D x+b2(N2-N)D x = 0.
|
|
|
(3.27) |
Le déterminant de (3.44) vaut
(N-1)D x (N2-N1)D x=L(l2-L1).
Il est non nul si et seulement si les sous-domaines se
recouvrent, N2<N1. Alors, on a
b1=b2=0, U1=0 et U2=0. La solution de P'h est
alors unique.
Dans le cas où N1=N2, le déterminant de
(3.44) s'annule. Le système linéaire
admet une infinité de solutions
b1=(N1-N)/ (N1-1)b2,
b2=b2. Il en est alors de même du problème P'h qui
admet une infinité à un paramètre de solutions. Ces solutions
sont affines dans chacun des sous-ensembles d'indices N1 et N2.
On a ainsi montré le
Lemme 3.4.1 Le problème P'h (Eqs.
(3.38)-(3.40)-(3.42)-(3.43))
admet une unique solution ssi les sous-domaines
se recouvrent N2<N1. Dans ce cas, la solution
(U1,U2) du problème P'h est composée des
restrictions aux sous-ensembles d'indices de la solution
U du problème Ph (i.e. U1=U|N1 et
U2=U|N2).
3.4.2 Algorithme parallèle de résolution
du problème P'h (Algorithme de Schwarz
discret)
Nous considérons une méthode itérative
de résolution du problème P'h. On part de
U10 et U20 quelconques et on pose
|
|
ì
ï
ï
ï
ï
ï
ï
ï
ï
í
ï
ï
ï
ï
ï
ï
ï
ï
î |
| A1 U1n+1
=
|
æ
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
è |
|
ö
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
ø |
, |
|
|
|
|
|
(3.28) |
et
|
|
ì
ï
ï
ï
ï
ï
ï
í
ï
ï
ï
ï
ï
ï
î |
| A2 U2n+1
=
|
æ
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
è |
|
ö
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
ø |
, |
|
|
|
|
(3.29) |
Remarque 3.4.1 Une solution stationnaire de
l'algorithme est solution du problème P'h. Ceci prouve
que si l'algorithme converge (voir plus loin la discussion
suivant le chevauchement des sous-domaines), il converge vers
l'unique solution de P'h qui est la restriction aux
sous-domaines
W1 et
W2 de la solution u du problème Ph.
L'algorithme de Schwarz
(3.45)-(3.46) sera
donc une méthode itérative de résolution du problème Ph.
Pour étudier la convergence, on pose
E1n=(e1,jn)jÎ N1=U1n-U1 et
E2n=(e2,jn)jÎ N2=U2n-U2 où
(U1,U2) est la solution du problème
P'h. Par linéarité des équations, l'erreur vérifie
|
|
ì
ï
ï
ï
í
ï
ï
ï
î |
| A1 E1n+1
=
|
æ
ç
ç
ç
ç
è |
|
ö
÷
÷
÷
÷
ø |
, |
|
|
|
|
|
(3.30) |
et
|
|
ì
ï
ï
ï
í
ï
ï
ï
î |
| A2 E2n+1
=
|
æ
ç
ç
ç
ç
è |
|
ö
÷
÷
÷
÷
ø |
, |
|
|
|
|
(3.31) |
On a ainsi pour n³ 1, e1,jn=g1n
(j-1)D x et e2,jn=g2n (j-N)D x.
Les conditions de Dirichlet en j=N1 et j=N2 donnent
|
g1n+1 (N1-1)D x= g2n (N1-N)D
x |
| g2n+1 (N2-N)D x= g1n (N2-1)D
x |
On a donc
| g1n+1= |
|
g2n
= |
|
|
|
g1n-1
= |
|
|
|
g1n-1
º b g1n-1.
|
La relation est aussi valable pour g2n+1. Comme
1<N2£ N1<N, le terme b est toujours positif et
on a: b<1 N2<N1. Pour
N2=N1, on a
b=1 et l'algorithme stagne. On a prouvé le
Théorème 3.4.2 L'algorithme de Schwarz
(3.45)-(3.46)
converge si et seulement si les sous-domaines se
recouvrent (N2<N1).
Remarque 3.4.2 Le théorème est tout à fait similaire au
théorème 3.2.2 du cas continu.
Remarque 3.4.3 L'absence de convergence dans le cas sans
recouvrement est en accord avec le
fait que le problème P'h est alors mal posé.
Remarque 3.4.4 Les systèmes linéaires (3.45)
(resp.
(3.46))
ne sont pas
symétriques à la ligne correspondant à la
discrétisation au point
xN1-1 (resp.
xN2+1). Ils peuvent être symétrisés en
substituant
u1,N1n+1 par u2,N1n (resp.
u2,N2n+1 par u1,N2n) dans les lignes
correspondantes.
3.4.3 Reformulation avec des conditions de Robin -
Problème P''h
Le but de ce paragraphe est de coupler les systèmes
linéaires
(3.38)-(3.40) par
des conditions de Robin
(3.18)-(3.19) discrétisées
aux points xN1 et xN2 par (cf.
(3.31)):
|
|
|
+a
u |
|
- |
|
f(x |
|
) = -
( |
|
- |
|
f(x |
|
))
+a u |
|
(3.32) |
et (attention au changement de direction de la dérivée
normale: n2=-n1)
|
|
|
+ |
|
f(x |
|
)
+a
u |
|
= - ( |
|
+ |
|
f(x |
|
))
+a u |
|
(3.33) |
où a est un nombre strictement positif. Nous
désignerons encore par P''h le problème
constitué par les équations
(3.38)-(3.40)-(3.49)-(3.50)
Nous allons montrer que l'unique solution du problème
P''h est la restriction aux sous-ensembles
d'indices
N1 et N2 de la solution du
problème Ph (3.37) posé sur l'ensemble
des inconnues. Ce résultat est valable avec ou sans
recouvrement des sous-domaines.
Remarque
(Importante) 3.4.1 Les discrétisations des dérivées normales
(3.18)-(3.19) par
(3.49)-(3.50)
ne font pas appel aux
même points suivant que l'on soit dans le
sous-domaine 1 ou dans le sous-domaine 2. On
pourrait s'inquiéter des problèmes de consistance
avec le problème Ph. Comme le montre le
paragraphe Existence ci-dessous, la dépendance de
(3.49)
et (3.50) par rapport au second
membre
f assure l'équivalence des formulations.
Existence
On construit une solution de P''h à partir de la
solution
U du système (3.37) en posant
U1=(uj)jÎ N1 et U2=(uj)jÎ
N2. Le couple (U1,U2) ainsi formé
vérifie évidemment les équations
(3.38) et (3.40).
Vérifions que l'équation (3.49)
est satisfaite. Comme u1,N1=u2,N1 ceci
équivaut à montrer que
soit encore par définition de U1 et U2
En divisant par D x ceci équivaut à
Il s'agit du
schéma de discrétisation du Laplacien écrit au point
xN1. On montre de même que l'équation
(3.50) est satisfaite.
Unicité
Par linéarité, il suffit de considérer le cas homogène
g0=gL=f=0. Alors, d'après (3.38)
et (3.40), on a
et
où b1, b2Î IR. Les conditions de raccord
(3.49)-(3.50)
deviennent:
b1+a (b1(N1-1)D x) =
b2+a (b2(N1-N)D x)
et
-b2+a (b2(N2-N)D x) =
-b1+a (b1(N2-1)D x).
Il s'agit d'un système en b1, b2:
|
|
ì
í
î |
| b1(1+a (N1-1)D x)
-b2(1+a (N1-N)D x)=0 |
| b1(1-a (N2-1)D
x)+ b2 (-1+a(N2-N)D x = 0.
|
|
|
(3.34) |
Le déterminant de (3.51)
vaut
|
a D x (1-N)(2+a D
x (N1-N2))
=a L (2+a (L1-l2))
|
et est strictement positif et égal au déterminant de
(3.20). Le système
(3.51) admet donc une solution
unique. Il en est alors de même du problème P''h.
On a montré le
Lemme 3.4.3 Le problème P''h (Eqs.
(3.38)-(3.40)-(3.49)-(3.50))
admet une unique solution. La solution
(U1,U2) du problème P''h est composée des
restrictions aux sous-ensembles d'indices de la solution
U du problème Ph (i.e. U1=U|N1 et
U2=U|N2).
3.4.4 Algorithme parallèle de résolution
du problème P''h
Nous considérons une méthode itérative de résolution du
problème P''h. On part de U10 et U20
quelconques et on pose
|
|
ì
ï
ï
ï
ï
ï
ï
ï
ï
ï
í
ï
ï
ï
ï
ï
ï
ï
ï
ï
î |
| A1 U1n+1
=
|
æ
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
è |
|
ö
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
ø |
, |
|
|
|
|
|
|
|
(3.35) |
et
|
|
ì
ï
ï
ï
ï
ï
ï
ï
ï
ï
í
ï
ï
ï
ï
ï
ï
ï
ï
ï
î |
| A2 U2n+1
=
|
æ
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
è |
|
ö
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
ø |
, |
|
|
|
|
|
|
(3.36) |
Remarque 3.4.5 Une solution stationnaire de
l'algorithme est solution du problème P''h. Ceci prouve
que si l'algorithme converge (voir plus loin), il converge
vers l'unique solution de P''h qui est la restriction aux
sous-domaines
W1 et
W2 de la solution u du problème Ph.
L'algorithme de Schwarz
(3.52)-(3.53)
sera donc une méthode itérative de résolution du problème
Ph.
Pour étudier la convergence, on pose
E1n=(e1,jn)jÎ N1=U1n-U1 et
E2n=(e2,jn)jÎ N2=U2n-U2 où
(U1,U2) est la solution du problème
P''h. Par linéarité des équations, l'erreur vérifie
|
|
ì
ï
ï
ï
ï
ï
ï
í
ï
ï
ï
ï
ï
ï
î |
| A1 E1n+1
=
|
æ
ç
ç
ç
ç
è |
|
ö
÷
÷
÷
÷
ø |
, |
|
| |
|
|
|
|
|
|
(3.37) |
et
|
|
ì
ï
ï
ï
ï
ï
ï
í
ï
ï
ï
ï
ï
ï
î |
| A2 E2n+1
=
|
æ
ç
ç
ç
ç
è |
|
ö
÷
÷
÷
÷
ø |
, |
|
|
|
|
|
|
(3.38) |
On a ainsi pour n³ 1, e1,jn=g1n
(j-1)D x et e2,jn=g2n (j-N)D x.
Les conditions de Robin en j=N1 et j=N2 donnent
|
g1n+1 (1+ a (N1-1)D x)= g2n
(1+ a(N1-N)D x) |
| g2n+1 (-1+ a(N2-N)D x)= g1n
(-1+ a(N2-1)D x)
|
On a donc
| g1n+1= |
| 1+ a(N1-N)D x |
|
| 1+ a
(N1-1)D x |
|
g2n
= |
| 1+ a(N1-N)D x |
|
| 1+ a
(N1-1)D x |
|
|
| -1+ a(N2-1)D x |
|
| -1+ a(N2-N)D x |
|
º b g1n-1
|
où
| b= |
| 1+ a(N1-N)D x |
|
| -1+a(N2-N)D x |
|
|
| -1+ a(N2-1)D x |
|
| 1+ a(N1-1)D x |
|
.
|
La relation est aussi valable pour g2n+1. Le
paramètre a étant positif, on peut montrer qu'avec
ou sans recouvrement des sous-domaines,
-1<b < 1.
On a ainsi prouvé le
Théorème 3.4.4 Pour a>0, l'algorithme
(3.52)-(3.53)
converge.
Remarque 3.4.6 Contrairement à l'algorithme de Schwarz, le recouvrement des
sous-domaines n'est pas nécessaire pour assurer la convergence
de l'algorithme.
Remarque 3.4.7 Il est possible d'annuler b et donc d'avoir une
convergence en deux itérations en choisissant
a=1/ (N2-1)D x ou
bien a=1/ (N-N1)D x.