TD 6 - Algorithmes d'approximation géométrique

Introduction

Le but de ce TD est d'implémenter un algorithme d'approximation pour la reconstruction de courbes dans le plan. Il s'agit de la version simplifiée de la méthode de Christofides que nous avons vue en cours pour approximer le Traveling Salesman Problem (TSP) dans des espaces métriques, et il est utilisé dans le cadre de la reconstruction de courbes en toutes dimensions. Avant de demarrer, nous rappelons que la documentation de la bibliothèque Jcg est consultable ici.


1. Reconstruction de courbes par approximation de TSP

L'idée de base est la suivante: étant donné une courbe connexe C échantillonnée, une manière naturelle de reconstruire C
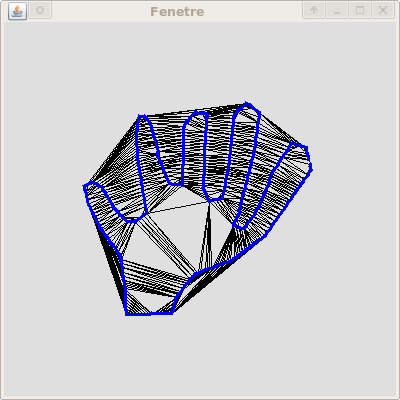
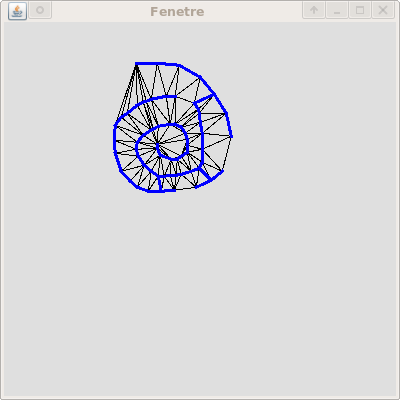
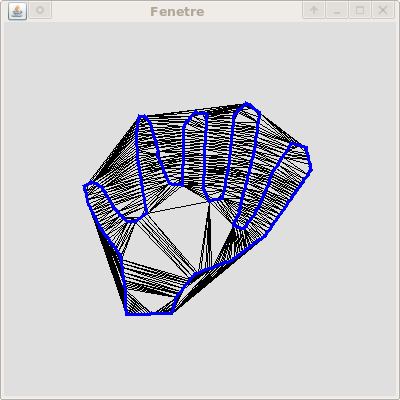
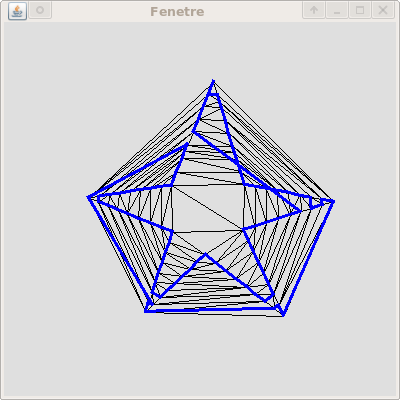
est simplement de construire le plus petit cycle hamiltonien reliant tous les échantillons. A priori ce cycle est calculé dans le graphe complet pondéré par la distance euclidienne. Cette idée a la fois simple et élégante est dûe à J. Giesen (voir l'article ici), qui a également montré qu'elle a du sens d'un point de vue théorique, à savoir : La conséquence des remarques ci-dessus est qu'il est possible de reconstruire des courbes en toutes dimensions par une technique basée sur la triangulation de Delaunay, sans avoir à calculer cette dernière ! Afin d'illustrer cette propriété nous allons considérer le cas des courbes planes. Ironiquement, dans ce cas le calcul explicite de la triangulation de Delaunay permet d'accélérer le processus (ce qui n'est pas le cas en dimensions 3 et plus).

Donc en gros, le travail à faire consiste à implementer la version simplifiée de l'algorithme de Christofides, à savoir :
  1. Calculer le Minimum Spanning Tree (MST) du nuage de points. Pour cela vous utiliserez l'algorithme de Kruskal. Toutefois, au lieu de travailler sur le graphe complet, vous travaillerez sur le graphe de la triangulation de Delaunay, dont les arêtes seront pondérées par la distance euclidienne entre leurs sommets. Ceci permettra de réduire la complexite de l'algorithme de O(n^2 log n) a O(n log n), tout en obtenant le meme resultat puisque nous savons depuis la séance 2 que le MST est inclus dans le graphe de Delaunay. Nous recommandons de coder le resultat du calcul dans la triangulation de Delaunay directement, en marquant simplement les arêtes du MST comme des arêtes de contrainte (en utilisant la methode mark() de la classe HalfedgeHandle).
  2. Dédoubler les arêtes du MST. Pour cela vous pourrez simplement faire en sorte que chaque arête de contrainte de la triangulation ait une arête symétrique elle-même marquée comme arête de contrainte. Ainsi votre MST dédoublé devient un sous-graphe eulérien du graphe de Delaunay, puisque tous ses sommets ont des degrés pairs.
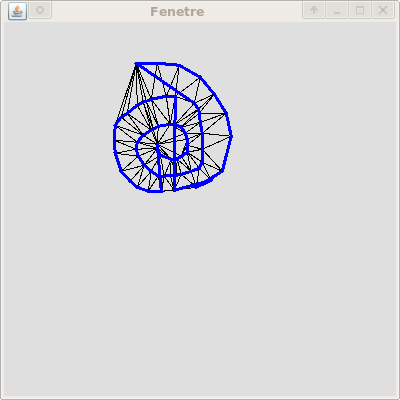
  3. Calculer un cycle eulérien dans le MST dédoublé, i.e. un cycle passant une et une seule fois par chaque arête orientée du MST. Pour ce faire nous recommandons d'utiliser l'algorithme suivant, qui est une version simplifiee de l'algorithme de Fleury : on parcourt les arêtes du MST de manière gloutonne, en commençant par une feuille et en "tournant" autour du MST toujours dans le meme sens (horaire ou anti-horaire). Afin d'éviter de repasser par une arête deja visitée, on la supprime du sous-graphe des qu'on la visite, ce que vous pourrez faire simplement en démarquant l'arete de Delaunay correspondante. Notez que cet algorithme est garanti de visiter toutes les aretes du MST par le fait qu'il tourne toujours dans le meme sens autour de l'arbre, qui dans le cas present est plonge dans le plan.
  4. Raccourcir le cycle eulérien. Pour cela il vous suffit de le parcourir une fois en eliminant tout sommet déjà visité lors du parcours (sauf le premier lors de la visite de la dernière arête du cycle). Ainsi vous obtiendrez un cycle hamiltonien, que vous retournerez sous la forme d'une liste de segments, de type List<Point_2[]>.
Pour l'implémentation, créez une classe TSP_2D dans laquelle vous ajouterez les méthodes suivantes :
Enfin, ajoutez une methode public List<Point_2[]> reconstruct() qui appelle les trois méthodes ci-dessus dans l'ordre pour produire la reconstruction. Pour lire l'entrée du programme, vous pourrez utiliser la classe IO fournie dans le fichier IO.java qui permet de lire des nuages de points stockés dans des fichiers.

Le code suivant (classe TSP_2D.java) vous permettra de tester votre programme :
public static void test (String filename) {
	TSP_2D tsp = new TSP_2D(filename);

	// compute MST
	tsp.computeMST();
		
	// Get list of constraint edges
	Collection<HalfedgeHandle<Point_2>> cEdgesDel = tsp.del.constraintEdges();
	Collection<Point_2[]> segments = new LinkedList<Point_2[]> ();
	for (HalfedgeHandle<Point_2> q : cEdgesDel)
		segments.add(new Point_2[] {q.getVertex(0).getPoint(), q.getVertex(1).getPoint()});

	// Show triangulation and MST in window
	Fenetre f1 = new Fenetre(false);
	Collection<TriangulationDSFace_2<Point_2>> facesDel = tsp.del.finiteFaces();
	LinkedList<Point_2[]> trianglesDel = new LinkedList<Point_2[]>();
	for (TriangulationDSFace_2<Point_2> fd : facesDel)
		trianglesDel.add(new Point_2[]{fd.vertex(0).getPoint(), fd.vertex(1).getPoint(), fd.vertex(2).getPoint()});
	f1.addTriangles(trianglesDel);
	f1.addFatSegments(segments);
	f1.setVisible();
		
	// re-initialize data structure
	tsp = new TSP_2D (filename);
		
	// compute TSP-based reconstruction
	List<Point_2[]> recons = tsp.reconstruct();

	// Show triangulation and MST in window
	Fenetre f2 = new Fenetre(false);
	f2.addTriangles(trianglesDel);
	f2.addFatSegments(recons);
	f2.setVisible();
	
	System.out.println("done.");
}
Pour tester, il vous faut donner un nom de fichier en entrée du programme. Vous pourrez utiliser les jeux de donnĂ©es suivants: hand.xy, star_uniform.xy et colimacon.xy qu'au TD 5. Vous devriez obtenir des résultats similaires à ceux présentés ci-dessous. Quels sont les défauts de l'approche ?

hand MST
 star MST
 colimacon MST
hand reconstruction
 star reconstruction
 colimacon reconstruction

Fig. 1 - Résultats de la procédure sur les trois jeux de données fournis. En haut, les MSTs. En bas, les reconstructions.

Voici une solution.