2 Arbres rouges et noirs
Dans cet exercice nous allons étudier les arbres rouges et noirs, qui sont une variante des arbres binaires de recherche permettant de garder un bon équilibre de l’arbre : la hauteur d’un arbre rouge et noir contenant n nœuds est O(log2n).
Un arbre rouge et noir est défini comme un arbre binaire de recherche dont les nœuds ont une couleur (rouge ou noir) et satisfaisant les conditions ci-dessous :
- la racine de l’arbre est noire et toutes les feuilles sont noires,
- les fils d’un nœud rouge sont noirs,
- pour tout nœud v de l’arbre, tous les chemins allant de v aux feuilles contiennent le même nombre de nœuds noirs.
class RBT extends IntegerPoint2D {
final static boolean RED = true;
final static boolean BLACK = false;
boolean color;
RBT left, right;
String element;
/* Construit un noeud d'un arbre binaire Rouge-Noir */
RBT(boolean color, RBT left, String element, RBT right) {
this.color = color;
this.left = left;
this.element = element;
this.right = right;
}
}On représente un arbre ou un sous-arbre par son nœud racine à l’aide de la classe RBT (Red-Black Tree). Un nœud contient un champ String element (la donnée à stocker), et des pointeurs vers les sous-arbres gauche et droit. On ajoute à chaque nœud l’information concernant sa couleur (champ boolean color). Les couleurs rouge et noire sont encodées par des constantes final static boolean RED et final static boolean BLACK.
Comme déjà fait auparavant (TD6 et cours), l’arbre vide est représenté par null. Les feuilles (qui sont noires) sont représentées par des nœuds sentinelles encodés par null (petits carrés noirs dans l’image ci-dessous).
Voici deux exemples d’arbres rouges et noirs :
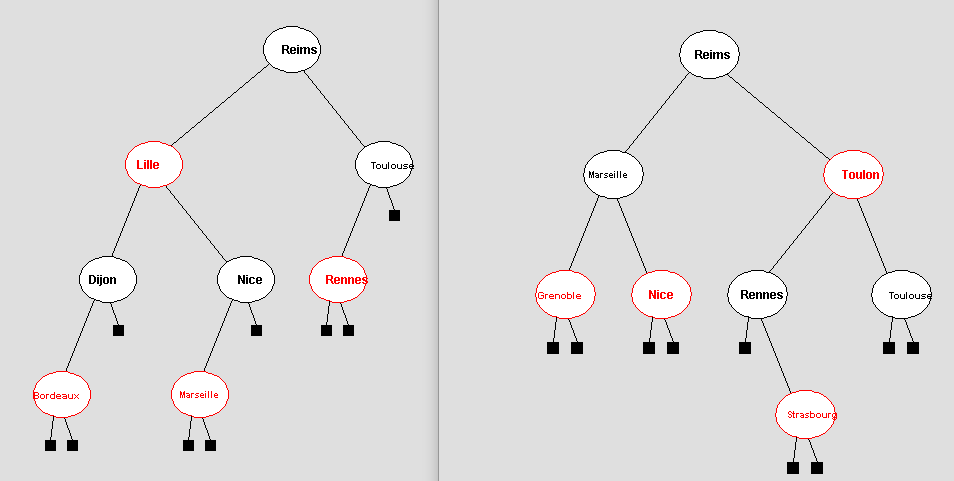
Lors du debugging de votre code, il pourrait s’avérer utile de visualiser un arbre t donné. Pour cela il suffit d’utiliser l’instruction
new DrawBinaryTree(t);
qui ouvre une fenêtre graphique et y dessine l’arbre comme dans l’exemple ci-dessus.
On souhaite implémenter une fonction qui teste si un arbre (qu’on suppose vérifier la condition des arbres binaires de recherche) est un arbre rouge et noir.
2.1 Validité des nœuds rouges
Dans la classe RBT, complétez la méthode boolean isRedValid(RBT t) qui renvoie true si l’arbre t vérifie la condition (2) pour tous les nœuds rouges.
Testez votre code avec la classe Test21.
Déposez RBT.java.
2.2 Validité des nœuds noirs
Dans la classe RBT, complétez la méthode boolean isBlackValid(RBT t) qui renvoie true si l’arbre t vérifie la condition (3) de la définition ci-dessus.
Testez votre code avec la classe Test22.
Déposez RBT.java.
2.3 Validité d’un arbre rouge et noir
Dans la classe RBT, complétez la méthode boolean isValid(RBT t) qui renvoie true si l’arbre t est un arbre binaire rouge et noir.
Testez votre code avec la classe Test23.
Déposez RBT.java.
2.4 Construction à partir d’une liste triée : estimation de la hauteur
Pour construire un arbre rouge et noir à partir d’une liste triée une solution simple à implémenter consiste à procéder de la manière suivante (illustrée par les images ci-dessous). D’abord on estime la hauteur finale de l’arbre rouge et noir (supposant qu’on essaie d’obtenir un équilibrage parfait). Ensuite on construit un arbre binaire de recherche dont tous les nœuds sont noirs, sauf éventuellement au dernier niveau (le seul qui pourrait être incomplet).
Voici quelques exemples d’arbres rouges et noirs construits avec cette stratégie à partir de listes triées de différentes tailles :
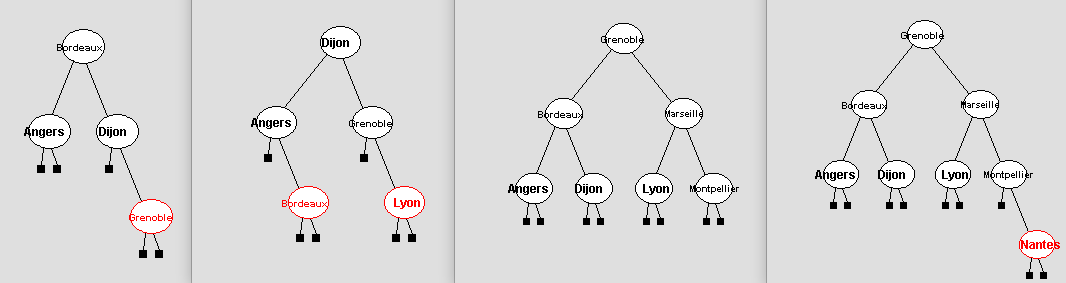
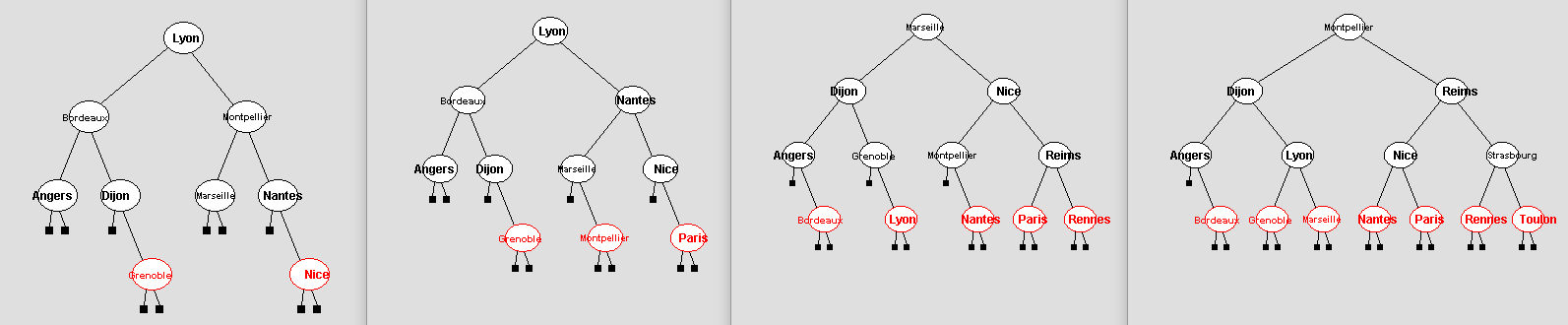
Dans la classe RBT, complétez la méthode int estimateBlackHeight(int n) qui renvoie l’entier h ≥ 0 satisfaisant (pour n ≥ 0) :
2h − 1 ≤ n < 2h + 1 − 1
Remarque : la fonction ci-dessus permet d’estimer le nombre de niveaux complets de l’arbre. On considère que pour l’arbre vide la fonction ci-dessus renvoie 0 (pas de nœuds internes) et pour un arbre de taille 1 (un seul nœud interne, la racine) elle renvoie 1.
Testez votre code avec la classe Test24.
Déposez RBT.java.
2.5 Construction à partir d’une liste triée : construction de l’arbre
Dans la classe RBT, complétez la méthode RBT ofList(LinkedList<String> l) qui renvoie un arbre binaire de recherche rouge et noir contenant les éléments de la liste l comme décrit plus haut.
Remarque : la fonction
ofList(LinkedList<String> l)peut modifier la listelen entrée (si cela peut s’avérer utile).
Testez votre code avec la classe Test25.
Déposez RBT.java.