


Chapter 8 Communications et routage
8.1 Généralités
On distingue généralement les
topologies statiques où le réseau d'interconnexion est fixe, en
anneau, tore 2D,
hypercube, graphe complet etc.
des topologies dynamiques, modifiées en cours d'exécution (par configuration
de switch).
Chaque topologie de communication a des
caractéristiques spécifiques, qui permettent de discuter de leurs qualités et de
leurs défauts. Ces caractéristiques sont, en fonction du nombre de processeurs interconnectés,
le degré du graphe d'interconnection, c'est-à-dire le nombre de processeurs interconnectés
avec un processeur donné, le diamètre, c'est-à-dire la distance maximale entre deux noeuds,
et le nombre total de liens, c'est-à-dire le nombre total de ``fils'' reliant les différents
processeurs. Les topologies de communications avec un petit nombre de liens sont plus économiques mais
en général leur diamètre est plus important, c'est-à-dire que le temps de communication
entre deux processeurs ``éloignés'' va être plus important. Enfin, on verra un peu plus loin
que le degré est également une mesure importante: cela permet d'avoir plus de choix pour
``router'' un message transitant par un noeud. On imagine bien également (thème développé
au chapitre 11, mais sous un autre point de vue), que si on a une panne au niveau d'un
lien, ou d'un processeur, plus le degré est important, plus on pourra trouver un autre chemin
pour faire transiter un message. Les caractéristiques de quelques topologies statiques classiques
sont résumées dans le tableau ci-dessous:
| Topologie |
# proc. |
do |
diam. |
# liens |
| Complet |
p |
p-1 |
1 |
p(p-1)/2 |
| Anneau |
p |
2 |
ë p/2 û |
p |
| Grille 2D |
sqrt(p)sqrt(p) |
2,3,4 |
2(sqrt(p)-1) |
2p-2sqrt(p) |
| Tore 2D |
sqrt(p)sqrt(p) |
4 |
2 ë sqrt(p)/2 û |
2p |
| Hypercube |
p=2d |
d=log(p) |
d |
p log(p)/2 |
L'intérêt est relatif, pour chaque choix. Par exemple, le
réseau complet est idéal pour le temps de communications (toujours unitaire)
mais le passage à l'échelle est difficile! (prix du cablage, comment rajouter des
nouveaux processeurs?).
La topologie en anneau n'est pas chère, mais les communications sont lentes,
et la tolérance aux pannes
des liens est faible.
On considère généralement que le tore 2D ou l'hypercube sont de bons compromis entre ces deux architectures.
8.2 Routage
On distingue deux modèles principaux, pour le routage des messages dans un système distribué.
Chaque modèle a un calcul de coût de communication distinct.
Le premier modèle est le modèle ``Store and Forward'' (SF):
chaque processeur intermédiaire reçoit et stocke le message M
avant de le re-émettre en direction du processeur destinataire. C'est un
modèle à commutation de message
qui équipait les premières générations de machines.
Le coût de communication est de d(x,y)(b+Lt) (où d(x,y) est la distance
entre les machines x et y, t est lié au débit du réseau, b est la
latence d'un envoi de message, et L est la longueur du message)
sauf programmation particulièrement optimisée (voir
section 8.3.5) où on peut atteindre Lt + O(sqrt(L)).
Le modèle ``cut-through'' (CT) utilise un
co-processeur de communication associé à chaque noeud.
Le coût de communication est de b+(d(x,y)-1)d+Lt (où d est
encore une fois lié au débit du réseau, t est la latence).
Si d << b, le chemin est calculé par le matériel, la partie logicielle
étant dans le facteur b.
Il existe également
deux principaux protocoles de routage: ``Circuit-switching'' (CC - ou ``commutation de
données'') et ``Wormhole'' (WH).
Le circuit-switching
crée le chemin avant l'émission des premiers octets. Le message est ensuite
acheminé directement entre source et destinataire. Cela nécessite une
immobilisation des liens (cas par exemple de l'iPSC d'INTEL).
Le protocole Wormhole
place l'adresse du destinataire dans l'entête du message.
Le routage se fait sur chaque processeur et le
message est découpé en petits paquets appelés flits.
En cas de blocage: les flits sont stockés dans les registres internes
des routeurs intermédiaires (exemple, Paragon d'INTEL).
En général,
CC et WH sont plus efficaces que SF. Ils masquent la distance entre les processeurs
communiquants.
CC contruit son chemin avant l'envoi des premiers paquets de données
alors que WH construit sa route tandis que le message avance dans le réseau
(meilleure bande passante que CC). Ces points sont résumés à la figure
8.1.
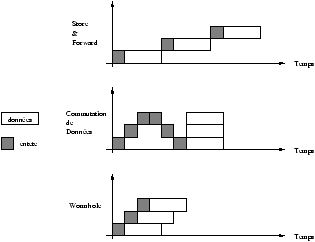
Figure 8.1: Comparaison CC, WH et SF
8.3 Algorithmique sur anneau de processeurs
8.3.1 Hypothèses
On étude une architecture
dans laquelle (voir figure 8.2 pour une explication graphique)
on a p processeurs en anneau,
chacun ayant accès à
son numéro d'ordre (entre 0 et p-1), par my_num()
et au nombre total de processeur par tot_proc_num (=p).
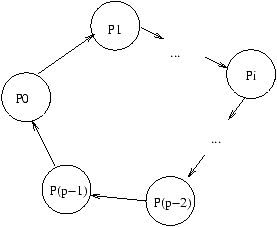
Figure 8.2: Architecture en anneau
En mode SPMD, tous les processeurs exécutent le même code,
ils calculent tous dans leur mémoire locale,
et ils peuvent envoyer un message au processeur de numéro
proc_num()+1[p]
par send(adr,L).
La variable adr contient l'adresse de la première valeur dans la mémoire
locale de l'expéditeur
et L est la longueur du message.
De même, ils peuvent recevoir un message de proc_num()-1[p] par
receive(adr,L).
Le premier problème auquel on est confronté, avant même de penser à implémenter
des algorithmes efficaces, est de s'arranger pour qu'à tout send corresponde un receive.
On peut faire plusieurs hypothèses possibles pour décrire la sémantique de telles primitives.
Les send et receive peuvent être bloquants comme dans OCCAM.
Plus classiquement, send est non bloquant mais receive est bloquant
(mode par défaut en PVM, MPI).
Sur des machines plus modernes, aucune opération n'est
bloquante (trois threads sont utilisés en fait: un pour le calcul, un pour le send et un pour le
receive).
La modélisation du coût d'une communication
est
difficile en général: ici envoyer ou recevoir un message de longueur L (au voisin immédiat) coûtera
b+Lt où
b est le coût d'initialisation (latence) et
t (débit) mesure la vitesse de transmission en régime permanent.
Donc, a priori, envoyer ou recevoir un message de longueur L de
proc_num()+/-q coûtera q(b+Lt). On verra que dans certains cas, on peut
améliorer les performances de communication en ``recouvrant'' plusieurs communications au même
moment (entre des paires de processeurs distincts).
8.3.2 Problème élémentaire: la diffusion
C'est l'envoi par un Pk d'un message de longueur L (stocké à l'adresse adr)
à tous les autres processeurs. C'est une primitive
implémentée de façon efficace dans la plupart des librairies de communications (PVM, MPI etc.).
On va supposer ici que le receive est bloquant.
broadcast(k,adr,L) { // emetteur initial=k
q = my_num();
p = tot_proc_num();
if (q == k)
(1) send(adr,L);
else
if (q == k-1 mod p)
(2) receive(adr,L);
else {
(3) receive(adr,L);
(4) send(adr,L);
}
}
L'exécution est décrite pour k=0 au temps 0
à la figure 8.3,
au temps b+Lt à la figure 8.4, au temps j(b+Lt) (j<p-1)
à la figure 8.5, et au temps (p-1)(b+Lt) à la figure 8.6.
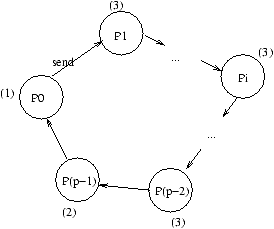
Figure 8.3: Exécution de la diffusion sur un anneau au temps 0.
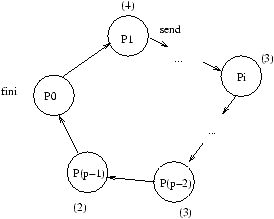
Figure 8.4: Exécution de la diffusion sur un anneau au temps b+Lt.
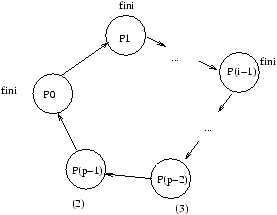
Figure 8.5: Exécution de la diffusion sur un anneau au temps i(b+Lt) (i<p-1).
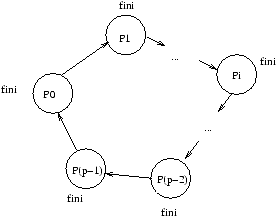
Figure 8.6: Exécution de la diffusion sur un anneau au temps (p-1)(b+Lt).
8.3.3 Diffusion personnalisée
On suppose toujours ici
un send non-bloquant et un receive bloquant.
On veut programmer un envoi par Pk
d'un message différent à tous les processeurs (en adr[q] dans Pk pour
Pq). A la fin, chaque processeur devra avoir son message à la location adr.
L'algorithme suivant opère en pipeline, et on obtient une bonne performance
grâce à un recouvrement entre les différentes communications!
Le programmme est le suivant:
scatter(k,adr,L) {
q = my_num();
p = tot_proc_num();
if (q == k) {
adr = adr[k];
for (i=1;i<p;i=i+1)
send(adr[k-i mod p],L); }
else
(1) receive(adr,L);
for (i=1;i<k-q mod p;i = i+1) {
(2) send(adr,L);
(3) receive(temp,L);
adr = temp; } }
Les exécutions pour k=0 aux temps 0
b+Lt, i(b+Lt) et
enfin (p-1)(b+Lt), sont représentées respectivement aux figures
8.7, 8.8, 8.9 et 8.10.
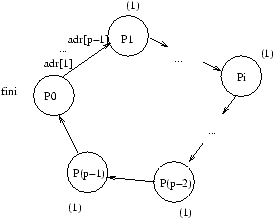
Figure 8.7: Exécution de la diffusion personnalisée au temps 0.
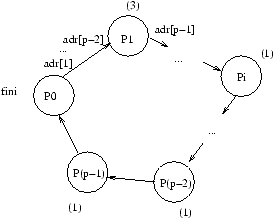
Figure 8.8: Exécution de la diffusion personnalisée au temps b+Lt.
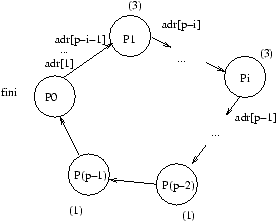
Figure 8.9: Exécution de la diffusion personnalisée au temps i(b+Lt).
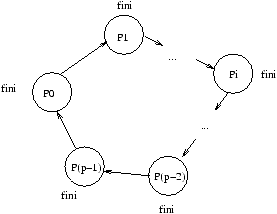
Figure 8.10: Exécution de la diffusion personnalisée au temps (p-1)(b+Lt).
8.3.4 Echange total
Maintenant, chaque processeur k veut envoyer un message à tous les autres.
Au départ chaque processeur dispose de son message à envoyer à tous les autres à la location
my_adr.
A la fin, tous ont un tableau (le même) adr[] tel que adr[q] contient le message
envoyé par le processeur q.
Il se trouve que par la même technique de recouvrement des communications, cela
peut se faire aussi en (p-1)(b+Lt) (et de même pour l'échange total personnalisé,
voir [RL03]).
Le programme est:
all-to-all(my_adr,adr,L) {
q = my_num();
p = tot_proc_num();
adr[q] == my_adr;
for (i=1;i<p;i++) {
send(adr[q-i+1 mod p],L);
receive(adr[q-i mod p],L);
}
}
8.3.5 Diffusion pipelinée
Les temps d'une diffusion simple et d'une diffusion personnalisée sont les mêmes; peut-on améliorer
le temps de la diffusion simple en utilisant les idées de la diffusion personnalisée?
La réponse est oui: il suffit de
tronçonner le message à envoyer en r morceaux (r divise L bien choisi).
L'émetteur envoie successivement les r morceaux, avec recouvrement partiel des communications.
Au début, ces morceaux de messages sont dans adr[1],...,adr[r] du
processeur k.
Le programme est:
broadcast(k,adr,L) {
q = my_num();
p = tot_proc_num();
if (q == k)
for (i=1;i<=r;i++) send(adr[i],L/r);
else
if (q == k-1 mod p)
for (i=1;i<=r;i++) receive(adr[i],L/r);
else {
receive(adr[1],L/r);
for (i=1;i<r;i++) {
send(adr[i],L/r);
receive(adr[i+1],L/r); } } }
Le temps d'exécution se calcule ainsi;
le premier morceau de longueur L/r du message sera arrivé au dernier processeur
k-1 mod p en temps (p-1)(b+L/rt) (diffusion simple).
Les r-1 autres morceaux arrivent les uns derrière les autres, d'où un temps supplémentaire
de (r-1)(b+L/rt).
En tout, cela fait un temps de (p-2+r)(b+L/r t).
On peut maintenant optimiser le paramètre r.
On trouve
ropt=sqrtL(p-2)t/b.
Le temps optimal d'exécution est donc de
Quand L tend vers l'infini, ceci est asymptotiquement équivalent à Lt, le facteur
p devient négligeable!
8.4 Election dans un anneau bidirectionnel
Chaque processeur part avec un
identificateur propre (un entier dans notre cas), et au bout d'un temps fini,
on veut que chaque processeur termine avec l'identificateur d'un même processeur,
qui deviendra ainsi le ``leader''.
Dans la suite, les processeurs vont être organisés en anneau bidirectionnel
synchrone:
-
Les n processeurs sont numérotés de P0 jusqu'à Pn-1. Par abus
de notation, on ne décrira pas les indices des processeurs modulo n. Ainsi,
par exemple, Pn est identifié à P0.
- Chaque processeur
Pi peut envoyer un message send(adr,L,sens) dont le
contenu se trouve dans sa mémoire locale à l'adresse adr, et consiste en
L entiers. La nouveauté est que Pi peut envoyer vers son voisin Pi+1,
en faisant sens=+, mais aussi vers Pi-1, en faisant sens=-.
- De même, la réception s'écrira maintenant recv(adr,L,sens). Un recv(adr,L,+)
sur Pi+1 réceptionnera le message émis par Pi, qui aura fait send(adr,L,+)
(et de façon similaire pour le -).
- On va maintenant supposer que les processus ne connaissent pas leur indice, et donc pas ceux
de leurs voisins non plus. Le processeur Pi n'a au départ dans sa mémoire locale qu'un entier
pidi représentant son identificateur, et un autre entier leader initialement à zéro.
Chaque pidi est unique, c'est-à-dire que
pidi=pidj implique i=j. Le but de l'algorithme d'élection est qu'un seul processus termine
avec leader=1.
- On prend une hypothèse d'exécution synchrone: tous les codes seront écrits en mode SPMD,
c'est-à-dire que le même code sera exécuté par tous les processeurs, et tous les send
(respectivement recv) seront exécutés exactement au même moment, que l'on appellera
étape: pour simplifier, on ne comptera que le nombre de recv. Un processeur est à l'étape k s'il
a effectué exactement k recv.
Cela implique donc
que ni les send ni les recv ne sont bloquants, par contre, si on n'a envoyé aucun
message à un processus Pi, alors recv fait sur Pi renverra le booléen faux (false),
sinon, il renvoie le booléen vrai (true).
8.4.1 Algorithme de Le Lann, Chang et Roberts (LCR)
Dans cet algorithme, chaque processeur va essentiellement essayer de diffuser son identificateur aux autres processus. Le processus
ayant l'identificateur le plus grand deviendra leader.
Les messages doivent tous transiter dans le même sens, soit +, soit -.
Au lieu de faire une diffusion complète, on peut s'arranger pour que quand un processus reçoit un identificateur,
il le compare avec le sien: si celui qu'il a reçu
est strictement plus grand que le sien, il continue à le passer sur le réseau. S'il est égal à
son identificateur, il se déclare leader, sinon il ne fait rien.
On enlève ainsi certaines communications inutiles.
Chaque processus fait:
LCR() {
send(pid,1,+);
while (recv(newpid,1,+)) {
if (newpid==pid)
leader = 1;
else if (newpid>pid)
send(newpid,1,+);
}
}
Cet algorithme permet bien d'élire un leader. En effet,
soit imax le numéro du processeur ayant l'identificateur pidimax maximal.
Soit 0 £ r £ n-1. On peut voir facilement par induction sur r que après r étapes,
la valeur de newpid sur le processeur Pimax+r est pidimax.
Ainsi, à l'étape n, Pimax+n=Pimax aura reçu son numéro
d'identificateur et en déduira qu'il est le leader.
Il faut maintenant voir que personne d'autre ne croit être le leader.
On peut voir par induction sur r que pour toute étape r, pour tous i et j, si i ¹ imax
et imax £ j < i, alors Pj envoie un message différent de pidi.
Alors nécessairement, seul Pimax peut recevoir son propre identificateur, et est donc le
seul leader possible.
Il faut n étapes et O(n2) communications.
Remarquez que l'on peut
relâcher l'hypothèse synchrone et se contenter d'un send non bloquant et d'un
recv bloquant, sans aucun changement dans l'algorithme.
8.4.2 Algorithme de Hirschberg et Sinclair (HS)
Cet algorithme fonctionne informellement de la façon suivante:
-
Chaque processeur Pi opère par phases, que l'on numérote à partir de 0.
- A chaque phase l, le processeur Pi envoie des tokens contenant son identificateur
dans les deux sens possibles, sur l'anneau.
- Ceux-ci vont parcourir une distance (nombre de noeuds traversés sur l'anneau)
de 2l au maximum (sous-phase d'envoi), avant d'essayer de revenir à leur emetteur Pi (sous-phase
de retour).
- Si les deux tokens reviennent, Pi continue avec la phase l+1.
- Quand l'identificateur pidi, émis par Pi, est dans la sous-phase d'envoi, et est réceptionné
par Pj, alors,
-
si pidi < pidj alors Pj ne fait rien,
- si pidi > pidj alors Pj continue à renvoyer (dans la sous-phase envoi ou retour, selon
la distance déjà effectuée par le message pidi) le token contenant pidi,
- si pidi = pidj alors Pj devient leader.
- Dans la sous-phase retour, tous les processeurs relaient les tokens normalement.
Les tokens utilisés dans cet algorithme contiennent un identificateur, mais aussi un drapeau indiquant
si le message est dans la phase envoi ou dans la phase retour, et un compteur (entier), indiquant
la distance qu'il reste à parcourir dans la phase envoi avant de passer à la phase retour.
On n'essaiera pas de coder ces tokens, et on se contentera d'utiliser les fonctions (que l'on supposera
programmées par ailleurs) suivantes:
-
les tokens sont représentés par une classe JAVA token contenant un constructeur
token(int phase, int message) (phase est le numéro de phase à la création du token);
on supposera qu'un token est de taille L donnée,
- token incr(token x) incrémente la distance parcourue par le token x,
- boolean retour(token tok) renvoie true si le message encapsulé
dans tok a fini la sous-phase envoi, false sinon (par rapport au numéro de phase
encapsulé),
- int valeur(token x) renvoie le message (entier) encapsulé par le token x.
Le pseudo-code correspondant, pour l'algorithme HS, est alors:
HS() {
boolean leader, continuephase;
int l;
token plus, moins;
l = 0;
leader = false;
continuephase = true;
while (continuephase) {
send(token(l,pid),L,+);
send(token(l,pid),L,-);
continuephase = false;
while () {
if (recv(plus,L,+)) {
if (not retour(plus)) {
if (valeur(plus) > pid) {
plus = incr(plus);
if (retour(plus))
send(plus,L,-);
else
send(plus,L,+);
}
else if (valeur(plus) == pid) {
leader = true;
System.exit(0);
}
}
else
if (valeur(plus) == pid) {
l = l+1;
continuephase = true;
}
else
send(incr(plus),L,-);
if (recv(moins,L,-)) {
if (not retour(moins)) {
if (valeur(moins) > pid) {
plus = incr(moins);
if (retour(moins))
send(moins,L,+);
else
send(moins,L,-);
}
else if (valeur(moins) == pid) {
leader = true;
System.exit(0);
}
}
else
if (valeur(moins) == pid) {
l = l+1;
continuephase = true;
}
else
send(incr(moins),L,+);
}
}
}
Le nombre total de phases exécutées au maximum avant qu'un leader ne soit élu est évidemment
borné par 1+é log n ù, car si on a un processeur qui arrive à l'étape é log n ù,
il est nécessaire que son pid soit plus grand que tous les autres, comme 2é log n ù³ n.
Le temps mis par cet algorithme est donc de O(n). En effet, chaque phase l coûte au plus 2l+1
(c'est le nombre de recv maximum que l'on peut avoir dans cette phase, en même temps
par tous les processeurs impliqués dans cette phase). En sommant sur les O(log n) phases, on trouve O(n).
A la phase 0, chaque processus envoie un token dans chaque direction à la distance 1. Donc au maximum, il y a 4n messages
à cette phase (2n aller, et 2n retour).
Pour une phase l > 0, un processus envoie un token seulement si
il a reçu un des deux tokens qu'il a envoyés à la phase l-1. Ce n'est le cas que si il n'a pas trouvé
de processeur de pid supérieur à une distance au maximum de 2l-1, dans chaque direction sur l'anneau.
Cela implique que dans tout groupe de 2l-1+1 processeurs consécutifs, un au plus va commencer une phase l.
Donc on aura au plus
processeurs entrant en phase l. Donc le nombre total de messages envoyés en phase l sera
borné (car chaque token envoyé parcourt au plus 2l processeurs) par:
| 4 |
æ
ç
ç
è |
2l |
ê
ê
ê
ë |
|
|
ú
ú
ú
û |
ö
÷
÷
ø |
£ 8n |
Comme on a un nombre de phases en O(log n), on en déduit un nombre de communications
de l'ordre de
O(n log(n)).
On a moins de communications, et l'algorithme sera meilleur que LCR si le débit des canaux est
faible (moins de contention de messages).
8.5 Communications dans un hypercube
On va examiner successivement les chemins de communication
et en déduire les façon de router les messages dans un hypercube, puis appliquer tout cela au problème du
broadcast dans un hypercube.
8.5.1 Chemins dans un hypercube
Un m-cube est la donnée de
sommets numérotés de 0 à 2m-1.
Il existe une arête d'un sommet à un autre si les deux diffèrent seulement
d'un bit dans leur écriture binaire.
Par exemple, un 2-cube est le carré suivant:
00 ®0 01
¯1 ¯1
10 ®0 11
où les numéros sur les arcs indiquent le numéro du lien (ou du canal) sortant
du noeud correspondant.
Soient A, B deux sommets d'un m-cube, et H(A,B) leur distance de Hamming (le nombre
de bits qui diffèrent dans l'écriture).
Alors il existe un chemin de longueur H(A,B) entre A et B (récurrence
facile sur H(A,B)). En fait,
il existe H(A,B)! chemins entre A et B, dont seuls H(A,B)
sont indépendants (c'est-à-dire qu'ils passent par des sommets différents).
Un routage possible est le suivant. On ``corrige'' les bits de poids faibles d'abord.
Par exemple, pour A=1011, B=1101,
on fait:
A xor B=0110 (ou exclusif bit à bit).
A envoie donc son message sur le lien 1 (c'est à dire vers 1001)
avec en-tête 0100.
Puis 1001, lisant l'entête, renvoie sur son lien 2, c'est à dire
vers 1101=B.
On peut également écrire un algorithme dynamique
qui corrige les bits selon les liens disponibles (voir à ce propos [RL03]).
8.5.2 Plongements d'anneaux et de grilles
Le code de Gray Gm de dimension m est défini récursivement par:
Gm = 0Gm-1 | 1 Gm-1rev
-
xG énumère les éléments de G en rajoutant x en tête de
leur écriture binaire,
- Grev énumère les éléments de G dans l'ordre renversé,
- | est la concaténation (de ``listes'' de mots binaires).
Par exemple:
-
G1={0,1},
- G2={00,01,11,10},
- G3={000,001,011,010,110,111,101,100},
- G4={0000,0001,0011,0010,0110,0111,0101,0100,1100,
1101,1111,1110,1011,1010,1001,1000}.
(imaginer la numérotation des processeurs sur l'anneau, dans cet ordre - un seul
bit change à chaque fois)
L'intérêt des codes de Gray
est qu'ils
permettent de définir un anneau de 2m processeurs dans le m-cube grâce
à Gm. Ils permettent
également de définir un réseau torique de taille 2r × 2s dans un
m-cube avec r+s=m (utiliser le code Gr × Gs).
On trouvera un exemple de plongement d'anneau dans l'hypercube à la figure 8.11.
On reconnaît l'anneau sur l'hypercube à la droite de cette figure, matérialisé
par des arcs gras.
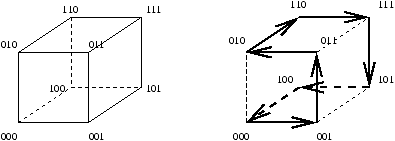
Figure 8.11: Plongement d'un anneau dans un hypercube.
8.5.3 Diffusion simple dans l'hypercube
On suppose que le processeur 0 veut envoyer un message à tous les autres.
Un premier algorithme naïf est le suivant: le processeur 0 envoie à tous ses voisins, puis
tous ses voisins à tous leurs voisins etc.: ceci est très inefficace, car
les messages sont distribués de façon très redondante!
On peut penser à un deuxième algorithme naïf, mais un peu moins: on utilise le code de Gray et on utilise la diffusion
sur l'anneau.
Mais il y a mieux, on va utiliser les
arbres couvrants de l'hypercube.
On se donne les primitives suivantes:
send(cube-link,send-adr,L),
et receive(cube-link, recv-adr,L).
On fait en sorte que
les processeurs reçoivent le message sur le lien correspondant
à leur premier 1 (à partir des poids faibles),
et propagent sur les liens qui précèdent ce premier 1.
Le processeur 0 est supposé avoir un 1 fictif en position m.
Tout ceci va se passer en m phases, i=m-1 ® 0.
En fait, on construit à la fois un arbre couvrant de l'hypercube et l'algorithme
de diffusion (voir la figure 8.12 dans le cas m=4).
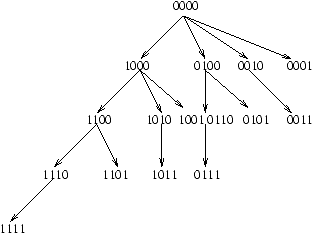
Figure 8.12: Un arbre couvrant pour un 4-cube.
Sans entrer dans les détails, toujours pour m=4, on a les phases suivantes:
-
phase 3: 0000 envoie le message sur le lien 3 à 1000,
- phase 2: 0000 et 1000 envoient le message sur le lien 2, à 0100 et 1100
respectivement,
- ainsi de suite jusqu'à la phase 0.
Pour le cas général, on se reportera à [RL03].








