Chapter 7 Problèmes d'ordonnancement

7.1 Introduction

Revenons à la mémoire partagée... et aux PRAM! Le problème important qui va nous préoccuper dans ce chapitre est de paralléliser ce qui a priori prend le plus de temps dans un programme: les nids de boucle. Nous n'irons pas jusqu'à traiter la façon dont un compilateur va effectivement paralléliser le code, mais on va au moins donner un sens à ce qui est intrinsèquement séquentiel, et à ce qui peut être calculé en parallèle.

Avant de commencer, expliquons en quoi ceci est primordial, pour l'efficacité d'un programme parallèle. Supposons qu'après parallélisation, il reste une proportion de s (0 < s £ 1) de notre code qui soit séquentiel, et qu'il s'exécute sur p processeurs. Alors l'accélération du calcul complet par rapport à un calcul séquentiel sera au maximum de,

1-s

(maximum de 1/s pour s fixé); c'est la loi d'Amdahl.

Conséquence: si on parallélise 80 pour cent d'un code (le reste étant séquentiel), on ne pourra jamais dépasser, quelle que soit la machine cible, une accélération d'un facteur 5!

7.2 Nids de boucles

Un nid de boucles est une portion de code dans laquelle on trouve un certain nombre de boucles imbriquées. Le cas le plus simple de nid de boucles est le nid de boucles parfait, qui a la propriété que les corps de boucle sont inclus dans exactement les mêmes boucles.

Par exemple, le code plus bas est un nid de boucles:

for (i=1;i<=N;i++) {
  for (j=i;j<=N+1;j++)
    for (k=j-i;k<=N;k++) {
      S1;
      S2;
    }
  for (r=1;r<=N;r++)
    S3;
}

Par contre, ceci n'est pas un nid de boucles parfait: S1 et S2 sont englobées par les boucles i, j et k alors que S3 est englobée par les boucles i et r.

Dans le cas de nids de boucles parfaits, on peut définir aisément l'instance des instructions du corps de boucle, qui est exécutée à un moment donné. Ceci se fait à travers la notion de vecteurs d'itération. Ceux-ci sont des vecteurs de dimension n (n étant le nombre de boucles imbriquées), dont les composantes décrivent les valeurs des indices pour chacune des boucles. Pour les nids de boucles non-parfaits, les domaines d'itérations sont incomparables a priori. Il suffit de ``compléter'' les vecteurs d'itération de façon cohérente: I ® I

Par exemple, pour S3 on a un vecteur d'itération en (i,r) dont le domaine est 1 £ i, r £ N. Pour S1 on a un vecteur d'itération en (i,j,k) dont le domaine est 1 £ i £ N, i £ j £ N+1 et j-i £ k £ N. On note une instance de S à l'itération I, S(I). On supposera dans la suite de ce chapitre que les domaines d'itération forment des polyèdres (conjonction d'inégalités linéaires).

On définit également l'ordre séquentiel d'exécution qui décrit l'ordre d'exécution ``par défaut''. Ceci se définit de façon triviale, comme un ordre <_seq entre les instructions, quand on n'a pas de boucles. C'est l'ordre textuel <_text. En présence de boucle, on utilise en plus la notion de vecteur d'itération: une instance d'une instruction T au vecteur d'itération I, T(I), sera exécutée avant son instance au vecteur d'itération J, c'est à dire T(I) <_seq T(J) si I <_lex J où est <_lex est l'ordre lexicographique. De façon plus générale, on définit:

S(I) <_seq T(J)	Û
	(I <_seq J) ou
	(I = J et S <_text T)

A partir de là, on veut mettre en parallèle certaines instructions: une partie de l'ordre séquentiel que l'on vient de définir est à respecter absolument, une autre pas (permutation possible d'actions). On va définir un ordre partiel (dit de Bernstein), qui est l'ordre minimal à respecter pour produire un code sémantiquement équivalent à l'ordre initial. En fait, l'ordre séquentiel va être une extension de l'ordre partiel de Bernstein. Cet ordre partiel est défini à partir de 3 types de dépendances de données: flot, anti et sortie.

7.3 Dépendance des données

7.3.1 Définitions

On va en définir de trois sortes: flot, anti et sortie, toujours dirigées par l'ordre séquentiel. C'est à dire que si S(I) <_seq T(J), on a une:

Dépendance de flot de S(I) vers T(J): si un emplacement mémoire commun est en écriture pour S(I) et en lecture pour T(J)
Dépendance anti de S(I) vers T(J): si un emplacement mémoire commun est en lecture pour S(I) et en écriture pour T(J)
Dépendance de sortie de S(I) vers T(J): si un emplacement mémoire commun est en écriture pour S(I) et en écriture pour T(J)

Prenons l'exemple du programme suivant:

for (i=1;i<=N;i++)
  for (j=1;j<=N;j++)
    a(i+j) = a(i+j-1)+1;

Son graphe de dépendances, est donné à la figure 7.1. Les dépendances de flot sont représentées par les flèches pleines. Les dépendances anti et de sortie sont représentées par des flèches à traits pointillés.

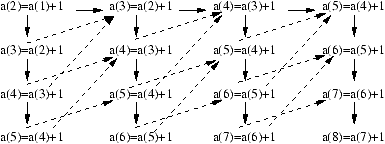
Figure 7.1: Dépendances flot, anti et de sortie.

7.3.2 Calcul des dépendances

Supposons que S(I) et T(J) accèdent au même tableau a (S en écriture, T en lecture par exemple, pour la dépendance de flot) S(I): a(f(I))=... et T(J): ...=a(g(J)); l'accès au tableau est commun si f(I)=g(J). Si f et g sont des fonctions affines à coefficients entiers cela peut se tester algorithmiquement en temps polynomial.

Chercher une dépendance de flot par exemple, revient à prouver en plus S(I) <_seq T(J). Encore une fois, cela se fait en général par la résolution de systèmes d'égalités et d'inégalités affines. Chercher les dépendances directes (c'est-à-dire celles qui engendrent par transitivité toutes les dépendances) est bien plus compliqué. Cela peut se faire par programmation linéaire, par des techniques d'optimisation dans les entiers etc.

Nous n'allons pas dans ce chapitre décrire ces algorithmes. Nous nous contenterons de montrer quelques exemples.

Prenons f(I)=i+j et g(J)=i+j-1 (ce sont les fonctions d'accès au tableau a dans l'exemple plus haut). On cherche les dépendances entre l'écriture S(i',j') et la lecture T(i,j):

f(I)=g(J) Û i'+j'=i+j-1
S(i',j') <_seq S(i,j) Û ( (i'£ i-1) ou (i=i' et j'£ j-1) )

Pour déterminer une dépendance de flot directe, on doit résoudre:

max_{<_seq} {(i',j') | (i',j') <_seq (i,j), i'+j'=i+j-1, 1 £ i,i',j,j' £ N }

La solution est:

(i,j-1)	si j ³ 2
(i-1,j)	si j=1

Pour déterminer une antidépendance directe de S(i,j) vers S(i',j'), on doit résoudre:

min_{<_seq} {(i',j') | (i,j) <_seq (i',j'), i'+j'=i+j-1, 1 £ i,i',j,j' £ N }

La solution (pour j³ 3, i£ N-1) est:

(i+1,j-2)

7.3.3 Approximation des dépendances

Les dépendances sont en général bien trop ardues à déterminer exactement. On s'autorise donc à n'obtenir que des informations imprécises, mais correctes. L'une d'elles est le Graphe de Dépendance Etendu (ou GDE):

Sommets: instances S_i(I), 1 £ i £ s et I Î D_{S_i}
Arcs: S(I) ® T(J) pour chaque dépendance

On appelle ensemble des paires de dépendances entre S et T l'ensemble suivant:

{(I,J) | S(I) ® T(J)} Í ZZ^n_S × ZZ^n_T

L'ensemble de distance de ces dépendances est:

{ (J-I) | S(I) ® T(J) } Í ZZ^n_S,T

Dans le cas de l'exemple de la section 7.3.1, on a des paires:

lecture a(i+j-1)-écriture a(i+j): ensemble de distance {(1,-2)}
écriture a(i+j)-lecture a(i+j-1): ensemble de distance {(1,0),(0,1)}
écriture a(i+j)-écriture a(i+j): ensemble de distance {(1,-1)}

Il reste un problème de taille: on ne peut pas calculer le GDE à la compilation! (de toutes façons, il est encore bien trop gros)

On doit donc abstraire encore un peu plus. On peut définir le Graphe de Dépendance Réduit ou GDR:

Sommets: instructions S_i (1 £ i £ s)
Arcs: e: S ® T si il existe au moins un arc S(I) ® T(J) dans le GDE
Etiquette: w(e) décrivant un sous-ensemble D_e de ZZ^n_S,T

Le tri topologique du GDR permet d'avoir une idée des portions séquentielles, et des portions parallélisables. On peut encore abstraire ce GDR en étiquetant ses arcs. Par exemple, on peut utiliser des niveaux de dépendance, que l'on définit plus bas, et on obtiendra le Graphe de Dépendance Réduit à Niveaux (GDRN).

On dit qu'une dépendance entre S(I) et T(J) est boucle indépendante si elle a lieu au cours d'une même itération des boucles englobant S et T; sinon on dit qu'elle est portée par la boucle. On étiquette en conséquence les arcs e: S ® T du GDR, par la fonction d'étiquetage l:

l(e)=¥ si S(I)® T(J) avec J - I=0
l(e) Î [1,n_S,T] si S(I) ® T(J), et la première composante non nulle de J-I est la l(e)^ieme composante

Prenons un exemple:

for (i=2;i<=N;i++) {
  S1: s(i) = 0;
  for (j=1;j<i-1;j++) 
    S2: s(i) = s(i)+a(j,i)*b(j);
S3:  b(i) = b(i)-s(i);
}

Le GDRN est représenté à la figure 7.2 (où a signifie dépendance anti, o de sortie et f de flot).

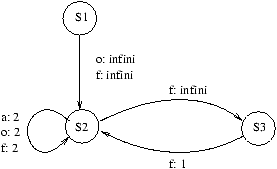
Figure 7.2: GDRN

Les vecteurs de direction sont une autre abstraction, en particulier de ces ensembles de distance:

on note z+ pour une composante si toutes les distances sur cette composante ont au moins la valeur z
on note z- pour une composante si toutes les distances sur cette composante ont au plus la valeur z
on note + à la place de 1+, - à la place de -1-
on note * si la composante peut prendre n'importe quelle valeur
on note z si la composante a toujours la valeur z

On obtient comme GDRV celui de la figure 7.3

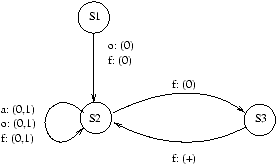
Figure 7.3: GRDV

7.4 Transformations de boucles

C'est là ce qui permet effectivement de paralléliser, à partir d'une connaissance minimale des dépendances: certaines dépendances autorisent à transformer localement le code, qui est à son tour bien plus parallélisable. Il existe deux types d'algorithmes bien connus:

Allen et Kennedy (basé sur le GDRN) : effectue des distributions de boucles
Lamport : transformations unimodulaires (basé sur le GDRV), c'est à dire, torsion, inversion et permutation de boucles

On décrira un peu plus loin l'algorithme d'Allen et Kennedy. Pour celui de Lamport, on reportera le lecteur à [RL03]. Avant d'expliquer comment on extrait d'un graphe de dépendance l'information nécessaire à la parallélisation, on commence par expliquer quelles sont les grands types de transformation (syntaxique) de code. Cela nous permettra de paralléliser un petit code, à la main, sans recourir à un algorithme de parallélisation automatique.

7.4.1 Distribution de boucles

Toute instance d'une instruction S peut être exécutée avant toute instance de T si on n'a jamais T(J) ® S(I) dans le GDE.

Plusieurs cas sont à considérer, pour le code:

for (i=...) {
  S1;
  S2;
}

Cas 1: S1 ® S2 mais on n'a pas de dépendance de S2 vers S1, alors on peut transformer le code en:

for (i=...)
  S1;
for (i=...)
  S2;

Cas 2: S2 ® S1 mais on n'a pas de dépendance de S1 vers S2, alors on peut transformer le code en:

for (i=...)
  S2;
for (i=...)
  S1;

7.4.2 Fusion de boucles

On transforme (ce qui est toujours possible):

forall (i=1;i<=N;i++)
 D[i]=E[i]+F[i];
forall (j=1;j<=N;j++)
 E[j]=D[j]*F[j];

en:

forall (i=1;i<=N;i++)
 {
  D[i]=E[i]+F[i];
  E[i]=D[i]*F[i];
 }

Cela permet une vectorisation et donc une réduction du coût des boucles parallèles, sur certaines architectures.

7.4.3 Composition de boucles

De même, on peut toujours transformer:

forall (j=1;j<=N;j++)
 forall (k=1;k<=N;k++)
  ...

en:

forall (i=1;i<=N*N;i++)
 ...

Cela permet de changer l'espace d'itérations (afin d'effectuer éventuellement d'autres transformations).

7.4.4 Echange de boucles

Typiquement, on transforme:

for (i=1;i<=N;i++)
 for (j=2;j<=M;j++)
  A[i,j]=A[i,j-1]+1;

en la boucle avec affectation parallèle:

for (j=2;j<=M;j++)
 A[1:N,j]=A[1:N,j-1]+1;

Ce n'est évidemment possible que dans certains cas.

7.4.5 Déroulement de boucle

Typiquement, on transforme:

for (i=1;i<=100;i++)
 A[i]=B[i+2]*C[i-1];

en:

for (i=1;i<=99;i=i+2)
 {
  A[i]=B[i+2]*C[i-1];
  A[i+1]=B[i+3]*C[i];
 }

7.4.6 Rotation de boucle [skewing]

C'est le pendant du changement de base dans l'espace des vecteurs d'itération. Typiquement:

for (i=1;i<=N;i++)
 for (j=1;j<=N;j++)
  a[i,j]=(a[i-1,j]+a[i,j-1])/2;

Il y a un front d'onde, et on peut le transformer en:

for (k=2;k<=N;k++)
  forall (l=2-k;l<=k-2;l+=2)
    a[(k-l)/2][(k+l)/2] = a[(k-l)/2-1][(k+l)/2]+a[(k-l)/2][(k+l)/2-1];
for (k=1;k<=N;k++)
  forall (l=k-N;l<=N-k;l+=2)
    a[(k-l)/2][(k+l)/2] = a[(k-l)/2-1][(k+l)/2]+a[(k-l)/2][(k+l)/2-1];

7.4.7 Exemple de parallélisation de code

On considère la phase de remontée après une décomposition LU d'une matrice.

Soit donc à résoudre le système triangulaire supérieur

Ux=b

avec,

æ
ç
ç
ç
è

U_1,1	U_1,2	U_1,3	···	U_1,n
0	U_2,2	U_2,3	···	U_2,n
			···
0	0	···	0	U_n,n

ö
÷
÷
÷
ø

et U_i,i ¹ 0 pour tout 1 £ i £ n.

On procède par ``remontée'' c'est à dire que l'on calcule successivement,

x_n

b_n

U_n,n

x_i

b_i -

j=i+1

U_i,j x_j

U_i,i

pour i=n-1,n-2,···,1.

Le code séquentiel correspondant est:

x[n]=b[n]/U[n,n];
for (i=n-1;i>=1;i--)
{  
x[i]=0;
for (j=i+1;j<=n;j++)
     L: x[i]=x[i]+U[i,j]*x[j];
     x[i]=(b[i]-x[i])/U[i,i];
     }

Son graphe de dépendances est donné à la figure 7.4, où on a essentiellement représenté les dépendances de flot. Il est à noter qu'il y a aussi des anti-dépendances des itérations (i,j) vers (i-1,j).

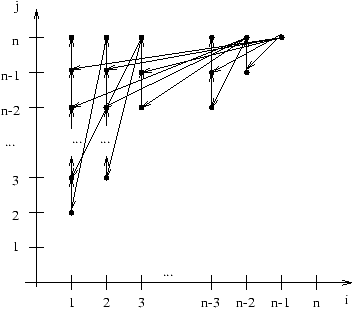
Figure 7.4: Graphe de dépendances de la remontée LU

En faisant une rotation et une distribution de boucles on arrive à paralléliser cet algorithme en:

H': forall (i=1;i<=n-1;i++)
       x[i]=b[i];
T': x[n]=b[n]/U[n,n];
H:  for (t=1;t<=n-1;t++)
     forall (i=1;i<=n-t;i++)
      L: x[i]=x[i]-x[n-t+1]*U[i],n-t+1];
     T: x[n-t]=x[n-t]/U[n-t,n-t];

Le ratio d'accélération est de l'ordre de n/4 asymptotiquement.

7.5 Algorithme d'Allen et Kennedy

Le principe est de remplacer certaines boucles for par des boucles forall et d'utiliser la distribution de boucles pour diminuer le nombre d'instructions dans les boucles, et donc réduire les dépendances. L'algorithme est le suivant:

Commencer avec k=1
Supprimer dans le GDRN G toutes les arêtes de niveau inférieur à k
Calculer les composantes fortement connexes (CFC) de G
Pour tout CFC C dans l'ordre topologique:
- Si C est réduit à une seule instruction S sans arête, alors générer des boucles parallèles dans toutes les dimensions restantes (i.e. niveaux k à n_S) et générer le code pour S
- Sinon, l=l_min(C), et générer des boucles parallèles du niveau k au niveau l-1, et une boucle séquentielle pour le niveau l. Puis reboucler l'algorithme avec C et k=l+1

Pour illustrer cet algorithme, on va prendre l'exemple suivant:

for (i=1;i<=N;i++) 
  for (j=1;j<=N;i++) {
    S1: a(i+1,j+1) = a(i+1,j)+b(i,j+2);
    S2: b(i+1,j) = a(i+1,j-1)+b(i,j-1);
    S3: a(i,j+2) = b(i+1,j+1)-1;
  }

On trouve les dépendances suivantes:

Flot S1 ® S1, variable a, distance (0,1),
Flot S1 ® S2, variable a, distance (0,2),
Flot S2 ® S1, variable b, distance (1,-2),
Flot S2 ® S2, variable b, distance (1,1),
Anti S1 ® S3, variable a, distance (1,-2),
Anti S2 ® S3, variable a, distance (1,-3),
Anti S3 ® S2, variable b, distance (0,1),
Sortie S1 ® S3, variable a, distance (1,-1).

Ce qui donne le GDRN de la figure 7.5.

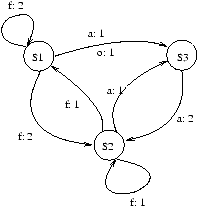
Figure 7.5: GDRN

Ce GDRN est fortement connexe et a des dépendances de niveau 1. La boucle sur i sera donc séquentielle. On enlève maintenant les dépendances de niveau 1 pour obtenir le GDRN modifié de la figure 7.6.

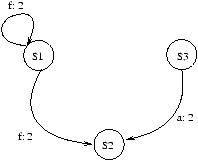
Figure 7.6: GDRN

La parallélisation finale est ainsi:

for (i=1;i<=N;i++) {
  for (j=1;j<=N;j++) 
    S1: a(i+1,j+1) = a(i+1,j)+b(i,j+2);
  forall (j=1;j<=N;j++)
    S3: a(i,j+2) = b(i+1,j+1)-1;
  forall (j=1;j<=N;j++)
    S2: b(i+1,j) = a(i+1,j-1)+b(i,j-1);
}