Chapter 4  Modèle PRAM

4.1  Introduction

• d'une suite d'instructions à exécuter plus un pointeur sur l'instruction courante,
• d'une suite non bornée de processeurs parallèles,
• d'une mémoire partagée par l'ensemble des processeurs.

• EREW (Exclusive Read Exclusive Write): seul un processeur peut lire et écrire à un moment donné sur une case donnée de la mémoire partagée.
• CREW (Concurrent Read Exclusive Write): plusieurs processeurs peuvent lire en même temps une même case, par contre, un seul à la fois peut y écrire. C'est un modèle proche des machines réelles (et de ce que l'on a vu à propos des threads JAVA).
• CRCW (Concurrent Read Concurrent Write): c'est un modèle étonnament puissant et assez peu réaliste, mais qu'il est intéressant de considérer d'un point de vue théorique. Plusieurs processeurs peuvent lire ou écrire en même temps sur la même case de la mémoire partagée. Il nous reste à définir ce qui se passe lorsque plusieurs processeurs écrivent au même moment; on fait généralement l'une des trois hypothèses suivantes:
  • mode consistant: tous les processeurs qui écrivent en même temps sur la même case écrivent la même valeur.
  • mode arbitraire: c'est la valeur du dernier processeur qui écrit qui est prise en compte.
  • mode fusion: une fonction associative (définie au niveau de la mémoire), est appliquée à toutes les écritures simultanées sur une case donnée. Ce peut être par exemple, une fonction maximum, un ou bit à bit etc.

4.2  Technique de saut de pointeur

for each processor i in parallel {
  y[i] = x[i]; 
}
while (exists object i s.t. next[i] not nil) {
  for each processor i in parallel {
    if (next[i] not nil) {
      y[next[i]] =_next[i] op_next[i](y[i],y[next[i]]);
      next[i] =_i next[next[i]];
    }
  }
}

• op_j pour préciser que l'opération op s'effectue sur le processeur j.
• =_j pour préciser que l'affectation est faite par le processeur j.

---

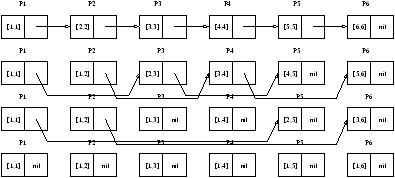
Figure 4.1: Technique du saut de pointeur.

---

y[i] =_i op_i(y[i],y[next[i]]);

y[next[i]] =_next[i] op_next[i](y[i],y[next[i]]);

for each processor i in parallel 
  A[i] = B[i];

for each processor i in parallel
  temp[i] = B[i];
for each processor i in parallel
  A[i] = temp[i];

d[i] = d[i]+d[next[i]];

temp[i] = d[next[i]];
d[i] = d[i]+temp[i];

public class SommePartielle extends Thread {

    int pos,i;
    int t[][];
    
    SommePartielle(int position,int tab[][]) {
      pos = position;
      t=tab;
    }

    public void run() {
      int i,j;
        
      for (i=1;i<=3;i++) {
        j = pos-Math.pow(2,i-1);
        if (j>=0) { 
          while (t[j][i-1]==0) {} ; // attendre que le resultat soit pret
          t[pos][i] = t[pos][i-1]+t[j][i-1] ; 
          } else {
        t[pos][i] = t[pos][i-1] ;
      };
    };
  }
}

import java.util.* ;

public class Exo3 {

    public static void main(String[] args) {
        int[][] tableau = new int[8][4];
        int i,j;
        Random r = new Random();
        
        for (i=0;i<8;i++) {
            tableau[i][0] =  r.nextInt(8)+1 ;
            for (j=1;j<4;j++) {
                tableau[i][j]=0;
            };
        };
        
        for (i=0;i<8;i++) {
            new SommePartielle(i,tableau).start() ;
        };
                
        for (i=0;i<8;i++) {
           while (tableau[i][3]==0) {} ;
        };
        
        for (i=0;i<4;i++) {
            System.out.print("\n");
            for (j=0;j<8;j++) {
                System.out.print(tableau[j][i]+" ");
            };
        };        
        System.out.print("\n");
    }
}

4.3  Circuit Eulerien

• int numero : numéro unique associé à chaque noeud,
• int profondeur : valeur à calculer,
• arbre_binaire pere : père du noeud courant de l'arbre,
• arbre_binaire fg,fd : fils gauche et droit du noeud courant dans l'arbre.

actif[0] = true; 
continue = true;
p = 0; /* p est la profondeur courante */

forall j in [1,n-1]
  actif[j] = false;

while (continue == true)
  forall j in [0,n-1] such that (actif[j] == true) {
    continue = false;
    prof[j] = p;
    actif[j] = false;
    if (fg[j] != nil) {
      actif[fg[j]] = true;
      continue = true; 
      p++; }
    if (fd[j] != nil) {
      actif[fd[j]] = true;
      continue = true; 
      p++; }

---

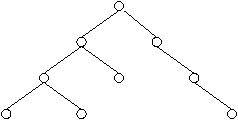
Figure 4.2: Un arbre binaire assez quelconque.

---

• successeur[3i] = 3fg[i] si fg[i] est différent de null et successeur[3i] = 3i+1 sinon.
• successeur[3i+1] = 3fd[i] si fd[i] est différent de null et successeur[3i+1] = 3i+2 sinon.
• successeur[3i+2] = 3pere[i]+2

4.4  Théorèmes de simulation

for each i from 1 to n in parallel 
  m[i] = TRUE;
for each i, j from 1 to n in parallel
  if (A[i] < A[j])
    m[i] = FALSE;
for each i from 1 to n in parallel
  if (m[i] == TRUE)
    max = A[i];

res = FALSE;
for each i in parallel {
  if (e == e[i])
    res = TRUE;

Théorème

---

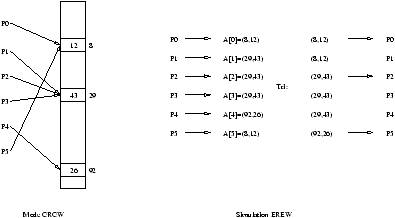
Figure 4.3: Codage d'un algorithme CRCW sur une PRAM EREW

---

Théorème (Brent)

for (k=m-1; k>=0; k--) 
  for each j from 2^k to 2^(k+1)-1 in parallel
    A[j] = max(A[2j],A[2j+1]);

Proposition

4.5  Tris et réseaux de tris

---

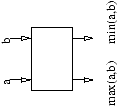
Figure 4.4: Un comparateur.

---

---

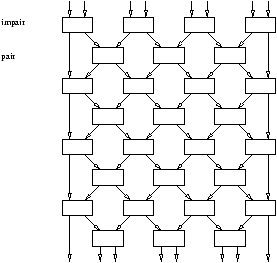
Figure 4.5: Réseau de tri pair-impair pour n=8.

---