1  Définition d'un jeu à deux joueurs

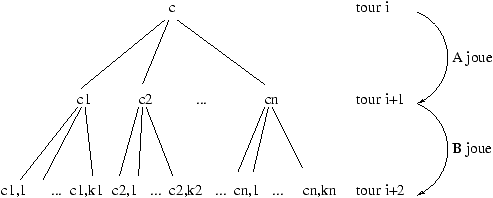
Un jeu à deux joueurs est défini classiquement comme un arbre qui a comme nœuds des positions (la racine est appelée la « position initiale du jeu »). Chaque nœud est un nœud « joueur » (i.e. c'est au joueur de jouer son coup) ou un nœud « opposant », et les joueurs s'alternent, de telle sorte qu'un nœud joueur a comme fils une liste de nœuds opposants, que l'on obtient à partir des différents coups disponibles (et symétriquement pour l'opposant). Si un nœud n'a pas de fils, c'est un nœud terminal, et dans ce cas on associe à ce nœud à l'aide d'une fonction h: noeudterminal -> R U {±infini;} une valeur qui indique ce que le résultat de la partie. Typiquement, si on s'intéresse seulement à des jeux comme les échecs, on aura +infini pour gain, -infini pour perte et 0 pour les autres positions (pat et autres nuls), mais il y a des jeux avec des structures d'évaluation plus complexes, par exemple les jeux où l'on mise de l'argent.

D'une certaine façon, cet arbre contient toutes les parties possibles que l'on peut jouer à partir de la position initiale. Si on a la possibilité d'explorer tout l'arbre, on peut déterminer s'il existe une stratégie gagnante pour le joueur. Si l'arbre est trop gros (ou si l'on impose des limites de temps) on se contente normalement d'explorer le sous-arbre obtenu en tronquant l'arbre de jeu à une certaine profondeur, et en évaluant les nœuds tronqués à l'aide d'une heuristique h'.

Dans les deux cas, il est déraisonnable de supposer que l'arbre de jeu est donné de façon extensive, et on préfère le présenter de façon implicite par des « règles de jeu » qui disent comment obtenir la liste des fils d'une position donnée.

2  La visite MinMax

• MinMax(p)=h(p) si p est une position terminale
• MinMax(p)=max(MinMax(o₁), ..., MinMax(o_n)) si p est une position joueur avec fils o₁, ..., o_n
• MinMax(p)=min(MinMax(j₁), ..., MinMax(j_m)) si p est une position opposant avec fils j₁, ..., j_m

• un type de données position qui permet de représenter les états possibles du jeu (et une position initiale) ;
• une fonction h : position -> R U {±infini} pour évaluer les positions terminales ;
• une fonction estjoueur : position -> {oui, non} qui sert à déterminer si une position est une position joueur ou opposant ;
• une fonction accessibles qui prenne une position p et retourne la liste des positions accessibles par les coups disponibles à partir de p.

3  La visite alpha-beta

Modules et foncteurs

Pour permettre de réutiliser le code écrit et de partager le travail en binômes, nous allons organiser l'écriture d'un jeu en plusieurs modules.

Les jeux

module type JEUX = sig
  type position
  val initiale : unit -> position
(* eval donne la valeur d'une position du point de vue du «joueur» :
   plus le gain est grand et plus c'est bon pour le joueur, plus il
   est petit et meilleur c'est pour l'opposant *)
  val eval : position -> gain
(* accessibles est la liste des positions possibles à partir d'un position *)
  val accessibles : position -> position list
  val affiche : position -> unit
(* demande_un_coup doit être une interface avec un utilisateur humain qui
   devra choisir un coup possible. Peut renoyer l'exeption Position_finale *)
  val demande_un_coup : position -> position
(* est_joueur renvoie true si dans la position passée en argument, c'est
   au joueur de jouer, et false si c'est à l'opposant.
   Peut renvoyer l'exception Position_finale *)
  val est_joueur : position -> bool
end

Les stratégies

module type STRATEGIE = functor (J : JEUX) -> sig
  type position = J.position
  val jouer : position -> position
end

Les parties

module Joueur = Strategie1(Jeu)
module Opposant = Strategie2(Jeu)

Travail en binôme, première étape

On propose donc de programmer ce TD en binôme, constitué d'un programmeur A et d'un programmeur B. Dans cette première étape, les tâches sont les suivantes :

1. Définir le type gain et l'exception Position_finale dans un fichier jeux.ml qui contiendra aussi les signatures JEUX et STRATEGIE.
   

   Solution jeux.ml

2. Le programmeur A implémente une STRATEGIE MinMax dans un fichier minmax.ml.
   

   Solution minmax.ml

3. Le programmeur B implémente un module de jeu au choix entre le jeu des allumettes et le jeu de la reine dans un autre fichier.

   Solution allumettes.ml
   

   Solution reine.ml

4. Le premier à avoir fini implémente le foncteur Partie dans un autre fichier.
   

   Solution partie.ml

5. Tester.

6. Implémenter la STRATEGIE humain qui se contente d'appeler demande_un_coup
   

   Solution humain.ml

7. Écrire un module principal pour lancer le jeu.
   

   Solution pour le jeu de la reine : main.ml

8. Jouer.

Deuxième étape, on change de rôle

1. Modifiez les signatures pour que les algorithmes puissent prendre en paramètre un nombre maximal de nœuds à visiter (limitant ainsi le temps de calcul et donc la puissance des joueurs automatiques).
2. Le programmeur A implémente un module de jeux puissance 4 en prenant bien soin de définir une valeur pour les positions non-terminales (cette valeur donne une estimation de la position pour le joueur).
3. Le programmeur B implémente la stratégie alpha-beta.
4. Jouez...

Annexe : les jeux

Le jeu des allumettes

Tic-Tac-Toe

Jeu de la reine

On propose une solution partielle pour l'implémentation du jeu de la reine.

Puissance 4