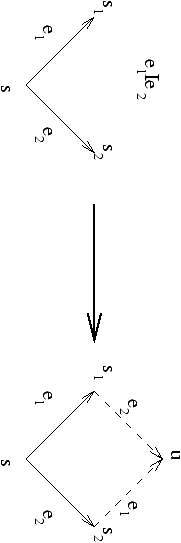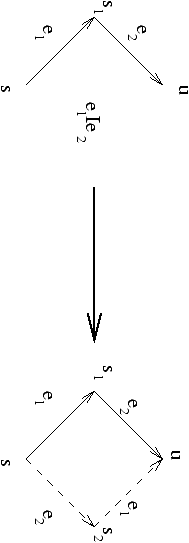Modèles du Vrai
Parallélisme

Eric Goubault
Commissariat à l'Energie Atomique, Saclay
email: Eric.Goubault@cea.fr
http://www.di.ens.fr/~goubault
http://www.enseignement.polytechnique.fr/profs/informatique/

Eric.Goubault

avec Pierre-Louis Curien (PPS)
James Leifer (INRIA Rocquencourt)
Jean-Jacques Lévy (INRIA Rocquencourt)
Catuscia Palamidessi (INRIA Futurs)

Exemple d'adjonction

Foncteur inclusion ST TS adjoint à gauche de Unfold: TS ® ST: Unfold(T=(S,i,L,Tran))=(S',i',L,Tran') avec,

S' est l'ensemble de toutes les suites de transitions finies (t₁,...,t_j,t_j+1,...,t_n-1) t.q. t_j=(s_j-1,a_j,s_j) et t_j+1=(s_j,a_j+1,s_j+1) (1<j<n)
i'=() la suite vide
Tran' consiste en tous les triplets (u,a,v) où u,v Î S' et u=(u₁,...,u_k), v=(u₁,...,u_k,(s,a,s')) obtenu en ajoutant une transition a à u

(en fait, coréflexion, on oublie les boucles - application: préservation des produits)

Systèmes de transition asynchrone

Définition 1 Un système de transition asynchrone est un quintuplet (S,i,E,I,Tran),

(S,i,E,Tran) est un système de transition,
I Í E × E est une relation symétrique irréflexive (la relation d'``indépendance'') telle que,
(1)
e Î E Þ $ s,s' Î S, (s,e,s') Î Tran
(2)
(s,e,s') Î Tran Ù (s,e,s'') Î Tran Þ s'=s''
(3)
e₁ I e₂ Ù (s,e₁,s₁) Î Tran Ù (s,e₂,s₂) Î Tran Þ $ u, (s₁,e₂,u) Î Tran Ù (s₂,e₁,u) Î Tran
(4)
e₁ I e₂ Ù (s,e₁,s₁) Î Tran Ù (s₁,e₂,u) Î Tran Þ $ s₂, (s,e₂,s₂) Î Tran Ù (s₂,e₁,u) Î Tran

Condition (3)

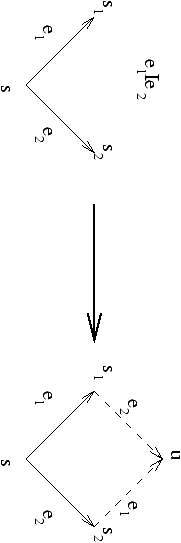
Condition (4)

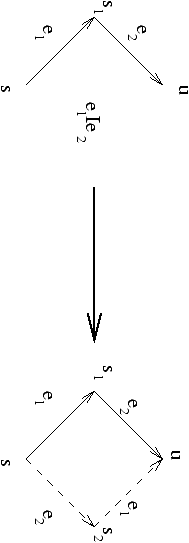
Morphismes

Ce sont les morphismes de systèmes de transition f préservant la relation d'indépendance:

a I b Þ f(a) I' f(b)

Produit cartésien

Soient T₀=(S₀,i₀,E₀,I₀,Tran₀) et T₁=(S₁,i₁,E₁,I₁,Tran₁) deux systèmes de transitions asynchrones. Leur produit T₀ × T₁ est (S,i,E,I,Tran) où,

le système de transitions sous-jacent (S,i,E,Tran) est le produit cartésien de (S₀,i₀,E₀,Tran₀) avec (S₁,i₁,E₁,Tran₁)
a I b ssi (p₀(a) et p₀(b) sont définis, implique p₀(a) I₀ p₀(b)) et (p₁(a) et p₁(b) sont définis, implique p₁(a) I₀ p₁(b))

Exercice: montrer que cela est bien un produit cartésien

Coproduit

Soient T₀=(S₀,i₀,E₀,I₀,Tran₀) et T₁=(S₁,i₁,E₁,I₁,Tran₁) deux systèmes de transitions asynchrones. Leur coproduit T₀ + T₁ est (S,i,E,I,Tran) où,

le système de transitions sous-jacent (S,i,E,Tran) est le coproduit de (S₀,i₀,E₀,Tran₀) avec (S₁,i₁,E₁,Tran₁)
a I b ssi (il existe a₀ et b₀ tels que a=j₀(a₀) et b=j₀(b₀) et a₀ I₀ b₀) ou (il existe a₁ et b₁ tels que a=j₁(a₁) et b=j₁(b₁) et a₁ I₀ b₁)

Système de transition concurrent

Définition 2 Un système de transition concurrent (CTS) est une structure (G,),

G=(O,A,dom,cod,id) est un graphe ``avec identités'' c.a.d.,
- O ensemble d'états,
- A ensemble de transitions,
- dom: A ® O relie les transitions à leurs états initiaux,
- cod: A ® O relie les transitions à leurs états finaux,
- id: O ® A relie chaque s Î O à une transition spéciale (les transitions ``*'' des systèmes de transition standards) id_s telle que dom(id_s)=s et cod(id_s)=s.

Suite

: Coin(G^#) ® A^# est l'opération résidu qui vérifie,
- G^# est le graphe augmenté (O^#,A^#,dom,cod,id) avec,
  - O^#=O È {W} (W n'appartient pas à O),
  - A^#=AÈ {w_q / q Î O^#}, dom(w_q)=q, cod(w_q)=W.
- Coin(X) (où X est un graphe) est l'ensemble des transitions coinitiales, c.a.d. l'ensemble des couples (t,u) de transitions t, u de X qui ont les mêmes états de départ.

soumis aux conditions suivantes,

(1) pour tout t Î A^# et u Î A^#,
- (a) dom (t u)=cod(u),
- (b) cod(t u)=cod(u t).
(2) pour tout t: q ® r Î A^#,
- (a) id_q t=id_r,
- (b) t id_q=t,
- (c) t t=id_r.
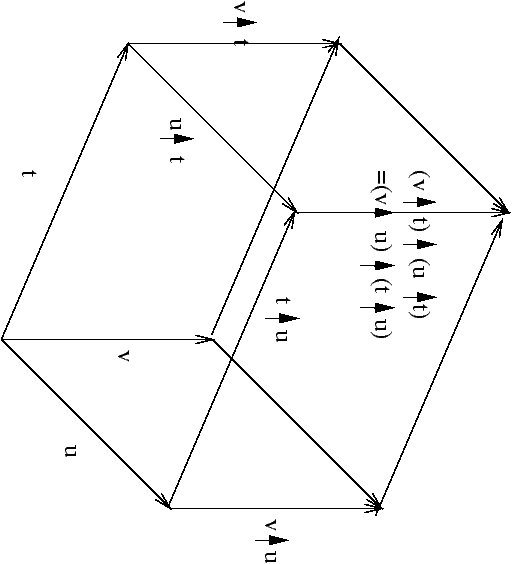
(3) pour toutes transitions coinitiales t, u, v dans A^#, (v t) (u t)=(v u) (t u) (l'``axiome du cube'')
(4) pour toutes transitions coinitiales t, u dans A^#, si t u et u t sont toutes les deux des identités alors t=u.

L'axiome du cube

Morphismes

Définition 3 Un morphisme de systèmes de transition concurrent est une paire de fonctions r=(r_O,r_A): (O,A,dom,cod,id,) ® (O',A',dom',cod',id',') telle que,

r_O: O ® O' et r_A: A ® A' sont des fonctions avec dom' ° r_A=r_O ° dom, cod' ° r_A=r_O ° cod et r_A ° id=id' ° r_O
Si t, u sont des transitions propres chérentes de C alors r(t u)=r(t) ' r(u).

Automates de trace

Un automate de trace est un triplet A=(E,Q,T),

E est un alphabet ``parallèle'', c'est à dire un ensemble d'événements sur lequel on a une relation binaire symétrique, irreflexive ||_E appelée relation de parallélisme
Q ensemble d'états,
T Í Q × (E È {e}) × Q ensemble de transitions.

Automates de Trace

Tout cela est soumis aux conditions suivantes,

q ®^e r ssi q=r,
si q ®^a r et q ®^a r' alors r=r' (similaire à la condition (2) des systèmes de transition asynchrones),
pour tous les états q et événements a, b, si a ||_E b, q ®^a r et q ®^b s alors pour un état p il existe des transitions s ®^a p et r ®^b p (similaire à la condition (3) des systèmes de transition asynchrones).

Equivalence par permutation et résidus

Idée similaire!

Langages de traces

(H,L) avec H un sous-ensemble non vide de chaines de L^*, clos par préfixes
(H,e,L,Tran)=ls(H,L) est un arbre de synchronisation ((h,a,h') Î Tran ssi h'=ha)
Inversement sl(T=(S,i,L,Tran)=(H,L) (T est un arbre de synchronisation) est un langage de traces (h Î L^* est dans H ssi il existe une suite de transitions dans T de la forme i ®^a₁ s₁ ®^a₂ s₂ ... ®^a_n s_n)

Reflexion (ou on oublie la structure de branchement - sl adjoint à gauche de ls)

Traces de Mazurkiewicz non-généralisées

(M,L,I) avec L un ensemble, I Í L × L symétrique irréflexive (relation d'indépendance) et M un sous-ensemble non vide de L^* t.q.:
- sa Î M implique s Î M pour tout sÎ L^*, a Î L
- sabt Î M et a I b implique sbat Î M pour tout s,t Î L^*, a,b Î L
- sa Î M et sb Î M et a I b implique sabÎ M pour tout sÎ L^*, a,b Î L

Equivalence de traces

Soit (M,L,I) un langage de trace. Pour s,t Î M on définit @ comme la plus petite relation d'équivalence t.q.

sabt @ sbat

si aI b, pour tout sabt,sbat Î M.

On appelle {s}_@ une trace de M.

Un exemple

Un distributeur VM de café (c) ou de thé (t) pour un coût de c₂
Un autre distributeur VM' de thé, pour un coût moindre c₁, mais qui peut tomber en panne (b)
Un consommateur C qui veut prendre un café pour c₂ ou un thé pour c₁

Un exemple

SYS=(VM | VM' | C) \ {b,c,c₁,c₂,t}

VM=c₂?.c!.VM + c₂?.t!.VM
c1?.t!.VM' + b.nil
c₂!.c?.C+c₁!.t?.nil

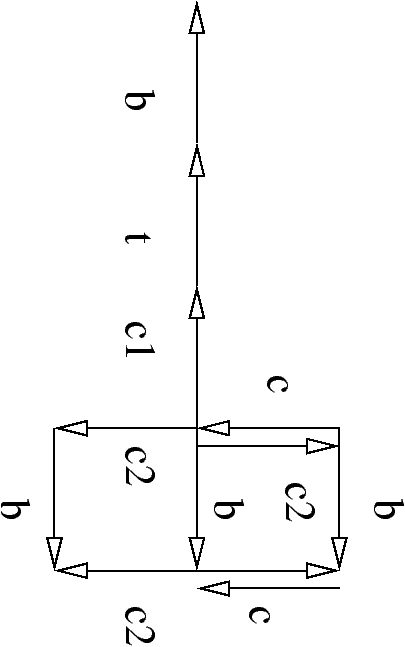
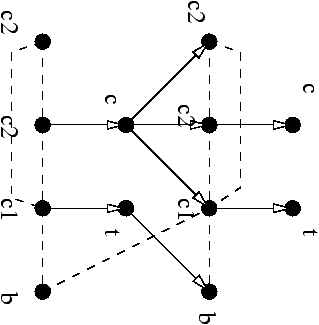
Système de transition

En suppose la synchronisation possible sur a? et a! donnant l'action observable a:

Langage de trace

On a au moins les traces {e,c₁,c₂,b,c₁t,c₂c,c₂b,bc₂,...}
On définit I comme étant la plus petite relation déquivalence telle que b I c et b I c₂

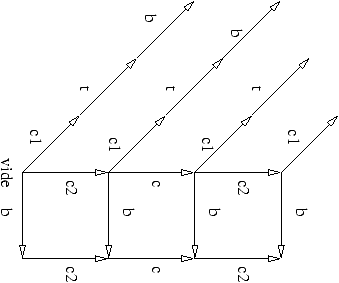
Ordre partiel sur les traces

(ne voit pas que le système peut avoir un point mort après que C fasse c₂! - il faudrait différencier les 2 types de c₂)

Propriétés

Soit (M,L,I) un langage de trace avec équivalence de trace @
Si su Î M et s @ s' alors s'u Î M et su @ s'u
La relation £ (s £ t si $ u, su @ t) est un préordre
Son quotient £ / @ est un ordre partiel de traces

Les traces de Mazurkiewicz généralisées

Définition 4 Un language de traces généralisé est un triplet (M,I,L) où,

L ensemble de symboles,
M Í L^*,
I: M ® 2^{L × L} est une fonction qui associe à chaque s Î M une relation I_s Í L × L.

Suite

tel que, si on définit @ comme la plus petite relation d'équivalence sur L^* telle que sabu @ sbau si a I_s b, et,

pour tous s Î M, I_s est symétrique et irréflexive,
(I est cohérente) s @ s' implique I_s = I_s',
(M est I-fermé) a I_s b implique sab Î M,
(I est cohérente)
- (i) a I_s b et a I_sb c et c I_sa b implique a I_sc b,
- (ii) a I_s c et c I_s b implique (a I_s b ssi a I_sc b).

Morphismes

Définition 5 Mazurkiewitz trace language!morphism of Soient (M,I,L) et (M',I',L') deux langages de trace généralisés. Une fonction partielle l: L ® L' est un morphisme de (M,I,L) vers (M',I',L') ssi,

l preserve les mots: s Î M implique l^*(s) Î M',
l respecte la relation d'indépendance:

a I_s b et l(a), l(b) definis implique l(a) I'_l^*(s) l(b) où l^* est une extension de l sur les mots définie comme suit,
- l^*(e)=e,
- l^*(sa)={
  
  l^*(s) l(a) si l(a) est defini
  
  l^*(s) sinon
  .

Relations systèmes de transitions asynchrones/langages de traces

On restreint d'abord la catégorie des systèmes de transitions asynchrones à TL₀ pour ne plus contenir que les langages de traces (M,E,I) tels que
" e Î E, $ s, seÎ M
Soit (M,E,I) un langage de traces dans TL₀ avec équivalence ~. On définit
tla(M,E,I)=(S,i,E,I,Tran)
- S=M/~ avec i={e}_~
- (t,e,t')Î Tran ssi $ s, se Î M such that t={s}_~ & t'={se}_~
Soit h: (M,E,I) ® (M',E',I') un morphisme de langages de traces. On définit tla(h)=(s,h) avec s({s}_~={h(s)}_~.

Relations systèmes de transitions asynchrones/langages de traces

Soit T=(S,i,E,I,Tran) un système de transitions asynchrones. On définit
atl(T)=(Seq,E,I)
- Seq est l'ensemble de toutes les chaines d'évenements e₁e₂... e_n pour lesquelles il y a des transitions (i₁,e1,s₁), (s₁,e₂,s₂), ..., (s_n-1,e_n,s_n) Î Tran
Soit (s,h): T ® T' un morphisme de systèmes de transitions asynchrones. On définit atl(s,h)=h.

tla et atl forment une adjonction...

Structures d'événements

Une structure d'événements première est une structure (E,£,#) où E est un ensemble d'événements partiellement ordonné par £ appelé relation de dépendance causale et où # Í E × E est une relation symétrique irreflexive, la relation de conflit satisfaisant,

{e' / e' £ e} est fini (axiome des ``causes finies''),
e # e' and e' £ e'' implique e # e'' (le conflit est héréditaire).

On écrit e co e' ssi ¬ (e £ e' ou e' £ e ou e # e').

Morphismes

Définition 6 Soit S={E,£,#} et S'={E',£',#'} des structures d'événements premières. Un morphisme de structures d'événe--ments de S vers S' est une fonction partielle f: E ® E' telle que,

si f(e) est définie alors {e' / e' £ f(e)} Í f({e'' / e'' £ e},
si f(e₀) et f(e₁) sont tous les deux définis f(e₀) # f(e₁) ou f(e₀)=f(e₁) implique e₀ # e₁ ou e₀=e₁.

NB: si f est définie, alors f préserve co.

Exemple

Ensemble de configurations

Soit (E,£,#) une structure d'événements. D(E,£,#) est l'ensemble des configurations de E, sous-ensembles x Í E de E qui sont,

sans conflit: pour tous e,e' Î x, e n'est pas en conflit avec e',
fermés vers le bas: pour tous e,e', e Î x et e' £ e implique e' Î x

On définit la configuration particulière é e ù={e'Î E | e' £ e}. On définit D⁰ les configuration finies.

Propriétés

e£ e' ssi " x Î D⁰(E,£,#), e' Î x implique eÎ x
e# e' ssi " x Î D⁰(E,£,#), e Î x implique e'Ïx
e co e' ssi $ x,x' Î D⁰(E,£,#), e Î x et e'Ïx et e Ïx' et e' Ïx' et xÈ x' Î D⁰(E,#,£).

Relation avec les systèmes de transition

Soit e Î E et c Î D(E,£,#) alors e est permis en la configuration c, ce que l'on écrit par c |- e si,

(i) e Ïc,
(ii) {e' / e' £ e Ù e' ¹ e} Í c,
(iii) e' Î E and e' # e implique e' Ïc

Les configurations finies sont des traces quand on ordonne ses éléments avec la dépendance causale. {e₁ < e₂ < ... < e_n} est une garantie pour c ssi {e₁,...,e_i-1} |- e_i pour i=1,...,n. On écrit aussi les garanties comme des chaines e₁... e_n.

Relation avec les systèmes de transition

Soient x,x' Î D(E,£,#). On écrit

x ®^e x' Û eÏx & x'=xÈ{e}

Exemple: un interrupteur parallèle

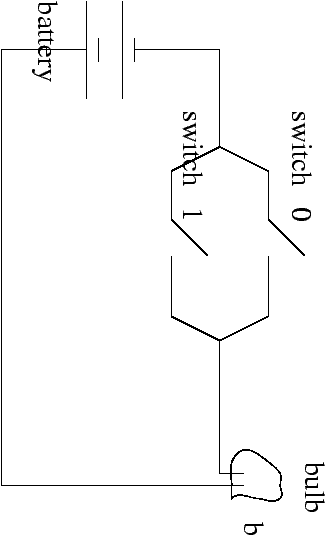
Exemple: les configurations correspondantes

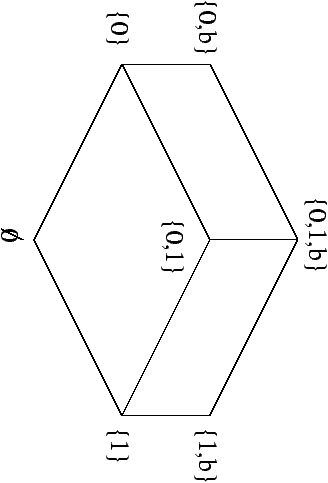
Propriétés catégoriques

Référence: Voir G. Winskel et al. (Models of Concurrency, Handbook in Logic in Computer Science, Vol.3).

Avec ces définitions, il est possible d'avoir des algèbres de modèles avec des équivalents pour les produits synchronisés etc.

Exercices

Produit cartésien de deux structures d'événements? (difficile)
Coproduit? (facile)
La traduction d'un système d'événement vers un système de transitions est claire (configurations...), dans l'autre sens?

This document was translated from L^AT_EX by H^EV^EA.

l^*(s) l(a)	si l(a) est defini
l^*(s)	sinon