Modèles du Vrai
Parallélisme

Eric Goubault
Commissariat à l'Energie Atomique, Saclay
email: Eric.Goubault@cea.fr
http://www.di.ens.fr/~goubault
http://www.enseignement.polytechnique.fr/profs/informatique/

Eric.Goubault

avec Pierre-Louis Curien (PPS)
James Leifer (INRIA Rocquencourt)
Jean-Jacques Lévy (INRIA Rocquencourt)
Catuscia Palamidessi (INRIA Futurs)

Remarques et références

On utilisera parfois le langage catégorique sans faire appel à une connaissance de la théorie. Il est néanmoins bon de savoir que tout peut être traité de façon générique
Référence: Saunders Mac Lane ``Categories for the working mathematician'', Giuseppe Longo et Andrea Asperti ``Categories for the working computer scientist''
Référence sur les modèles du parallélisme: Glyn Winskel ``Models for Concurrency'', Handbook of Logic in Computer Science, Vol. 4

Plan du cours

``Vrai'' et ``faux'' parallélisme
Rappels (rapides): systèmes de transitions et bisimulation
Une reformulation ``algébrique'' des constructions sur les systèmes de transitions, et de la bisimulation forte
Systèmes de transition asynchrones, concurrents,

Plan du cours

Automates de trace, traces de Mazurkiewicz (généralisées)
Structures d'évenements (étiquetées ou pas), pomsets et systèmes de transitions avec indépendance.
Réseaux de Petri
Comparaison des différents modèles, sémantiques vraiment parallèles de CCS et bisimulations sur les différents modèles
Quelques idées géométriques (si le temps le permet)

Motivation du cours

Grand nombre de modèles introduits à des niveaux d'abstraction différents (évenements/états, branchements ou pas etc.)
Par des correspondances (style correspondances de Galois, ou adjonctions en général), les constructions sémantiques utiles pour la sémantique du parallélisme sont définissables dans tous ces modèles de façon similaire (``produit cartésien'' = composition parallèle...)
Les congruences sémantiques peuvent aussi être définies de façon très générales sur tous ces modèles (ex. bisimulation forte, par ``span de morphismes ouverts'')
On illustrera tout cela sur un certain nombre de modèles les plus classiques, à commencer par la reformulation dans le cas des systèmes de transition.

Rappels -- Systèmes de transitions (cf. cours 3)

Définition 1 Un système de transitions est une structure

(S,i,L,Tran)

S ensemble d'états et i état initial,
L ensemble d'étiquettes, et
Tran Í S × L × S la relation de transition

Exemple

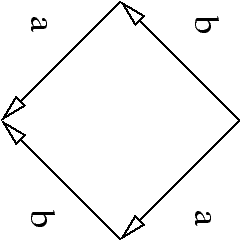
``Vrai'' et ``faux'' parallélisme

a | b ~ a.b+b.a?

Identifier non-déterminisme et parallélisme est moralement malsain:

Faut-il l'interpréter comme exclusion mutuelle entre a et b ou exécution asynchrone de a avec b?

Raffinement d'actions

D'un point de vue de l'ingéniérie, il est bon de pouvoir raisonner sur un système sans se préoccuper de tous les détails à grain fin, voire atomique
Þ trouver des méthodes sémantiques qui permettent de raffiner progressivement le grain (ou de composer les résultats acquis sur des sous-systèmes)
Exemple: on étudie a | b, mais a est en fait raffiné en a.a'

Raffinement d'actions

Si a | b ~ a.b+b.a, alors (a.a') | b et a.a'.b+b.a.a' doivent aussi être équivalents (si ~ est une congruence):

Mais il manque la trace a.b.a' dans le deuxième cas! (et on aime en général que ~ contienne l'équivalence de trace...)

Catégorie

On en fait une catégorie avec pour morphismes les simulations (Glynn Winskel et al.).

Un système de transition T₁ simule un système de transitions T₀ à la condition que si T₀ peut effectuer une action a dans un certain contexte, alors T₁ peut effectuer a également dans un contexte similaire.

Un morphisme f: T₀ ® T₁ definit la façon dont les états et les transitions de T₀ sont reliés aux états et transitions de T₁.

Morphismes

Définition 2 Soit T₀=(S₀,i₀,L₀,Tran₀) et T₁=(S₁,i₁,L₁,Tran₁) deux systèmes de transition. Un morphisme f: T₀ ® T₁ est un couple f=(s,l) où,

s: S₀ ® S₁,
l: L₀ ® L₁ est tel que s(i₀)=i₁ et
(s,a,s') Î Tran₀ Þ (s(s),l(a),s(s')) Î Tran₁

Morphismes partiels

Les morphismes partiels permettent à T₁ de ne pas effectuer d'action quand T₀ le fait.

Définition 3 Soient T₀=(S₀,i₀,L₀,Tran₀) et T₁=(S₁,i₁,L₁,Tran₁) deux systèmes de transition. Un morphisme partiel f: T₀ ® T₁ est un couple f=(s,l) où,

s: S₀ ® S₁,
l: L₀ ® L₁ est une fonction partielle. (s, l) est tel que
- s(i₀)=i₁,
- (s,a,s') Î Tran₀ et l(a) est défini implique (s(s),l(a), s(s')) Î Tran₁ . Sinon, si l(a) n'est pas défini alors s(s)=s(s').

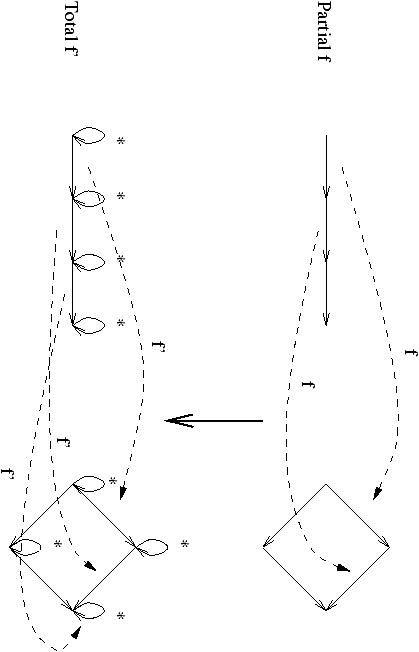
Transitions silencieuses

On complète un système de transition T=(S,i,L,Tran) en T_*=(S_*,i_*,L_*,Tran_*),

S_*=S,
i_*=i,
L_*=L È { * },
Tran_*=Tran È { (s,*,s) / s Î S }.

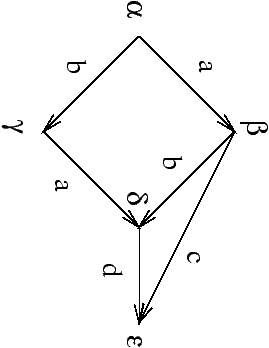
Exemple

Bisimulation - rappel, cours 3

Idée d'expérimentation formalisée:

Une relation binaire S Í P × P entre agents est une bisimulation (forte) si (P,Q) Î S implique, pour tout a Î S,

(i) dès que P ®^a P' il existe Q' tel que Q ®^a Q' et (P',Q') Î S,
(ii) dès que Q ®^a Q' il existe P' tel que P ®^a P' et (P',Q') Î S

Maintenant P et Q sont (fortement) équivalents ou (fortement) bisimilaires si et seulement si il existe une bisimulation S telle que (P,Q) Î S.

On écrit P ~ Q quand P et Q sont bisimilaires.

Exemple

On considère les agents A et B définis par:

A = a.A'

A'=

B = c.B'

B' =

Peut-on trouver un équivalent pour (A | B) \ c ?

Exemple

La réponse est oui

Soient,

C₀ =

.C₁ + a.C₂

C₁ = a.C₃

C₂ =

.C₃

C₃ = t.C₀

Alors, (A | B) \ c ~ C₁.

Preuve···

Exemple

Soit S= { ((A| B) \ c,C₁),((A'| B)\ c,C₃), ((A | B')\ c,C₀),((A'| B')\ c,C₂) }.

Alors S est une bisimulation forte. Il suffit de tester toutes les actions que les 8 agents peuvent exécuter, par exemple,

=1.75em

(A|

B') \ cC₀

^aet

^a(A | B) \ c(A' | B') \ cC₁C₂

Arbres de synchronisation (cf. cours 3)

Un arbre de synchronisation est un système de transition (S,i,L,tran) tel que:

tout état est atteignable
il n'y a pas de boucle non-triviale
(s',a,s) Î Tran et (s'',b,s) Î Tran implique a=b et s'=s''

Bran_L sera la sous-catégorie pleine de la catégorie des systèmes de transition sur l'alphabet L.

Bisimulations et morphismes

Soit M une catégorie de modèles (ici, par exemple, les systèmes de transition).
Soit P une sous-catégorie de ``chemins'' de M
Un chemin de XÎ M sera un morphisme p: P ® X pour un P Î P

Morphismes P-ouverts

Un morphisme est P-ouvert ssi pour tout diagramme commutatif:

P^pX^m_fQ^qY

il existe un morphisme p' tel que p' ° m=p et f ° p'=q.

Morphismes Bran_L-ouverts

Ce sont les morphismes ``zig-zag'' (s,Id_L): T ® T' tels que pour tout état s de T:

Si (s(s),a,s') est dans T', alors il existe un état u de T tel que (s,a,u) est dans T et s(u)=s'.

Preuve

Soit f un tel morphisme. Soit s un état atteignable de T tel que s(s) ®^a s' Î T'. Comme s est atteignable, il existe dans T:
i=s₀ ®^a₁ s₁ ®^a₂ ... ®^a_n s_n = s
Soit P Î Bran_L qui est exactement cette suite de transitions et p: P ® T le morphisme inclusion
Soit Q Î Bran_L:
®^a₁ ®^a₂ ... ®^a_n ®^a
et q: Q ® T' le morphisme dont l'image est:
s(s₀) ®^a₁ s(s₁) ®^a₂ ... ®^a_n s(s) ®^a s'

Preuve

Soit m: P ® Q le morphisme inclusion dans Bran_L. Le diagramme suivant commute:
P^pT^m_fQ^qT'
f est un morphisme ouvert donc il existe r: Q ® T tel que les deux triangles commutent.
L'état final de Q donne s' ®^a u dans T tel que s(u)=s'.

Preuve

A l'inverse, si f satisfait la condition zig-zag, et si on suppose que l'on a un diagramme commutatif:
P^pT^m_fQ^qT'
A isomorphisme près, Q est simplement une extension de P par des transitions simples.
Par itération de la condition zig-zag, on obtient un morphisme r: Q ® T tel que r° m=p et f ° r=q.

P-bisimilarité

X₁ et X₂ du modèle M sont P-bisimilaire si il existe un span de morphismes P-ouverts:

X^f₁^f₂X₁X₂

P-bisimilarité et bisimilarité forte

Deux systèmes de transition avec le même alphabet L sont Bran_L-bisimilaires ssi ils sont fortement bisimilaires au sens de Milner.

Preuve

Si deux systèmes de transition sont connectés par un morphisme ouvert (vis-à-vis de Bran_L), sa restriction aux états vérifie la condition zig-zag. Cela implique que son graphe sous-jacent est une bisimulation forte.
La bisimulation forte étant une relation d'équivalence, un span de morphismes Bran_L-ouverts les rend donc bisimilaires

Preuve

Soit R une bisimulation forte entre T₁ et T₂
On construit un système de transition T_L à partir de R:
- l'ensemble de ses états et R, avec état initial (i₁,i₂) (la paire d'états initiaux de T₁ et de T₂)
- ses transitions sont ((s₁,s₂),a,(s₁',s₂')) où (s₁,s₂) Î R et (s₁',s₂') Î R pour lesquelles (s₁,a,s₁') Î T₁ et (s₂,a,s₂') Î T₂.

Preuve

On a des morphismes évidents f₁: R ® T₁, f₂: R ® T₂ (projections)
Comme R est une bisimulation forte, f₁ et f₂ satisfont la condition zig-zag, et donc forment un span de morphismes Bran_L-ouverts.

Produits Cartésiens

Comme dans les ensembles, ils vérifient la ``propriété universelle'':

" Y^{" f₁}^{$ ! h}^{" f₂}X₁ × X₂^p₁^p₂X₁X₂

Produits Cartésiens

Soient deux systèmes de transitions T₀=(S₀,i₀,L₀,Tran₀) et T₁=(S₁,i₁,L₁,Tran₁). Leur produit est T₀ × T₁=(S,i,L,Tran) avec,

S=S₀ × S₁ et i=(i₀,i₁). Soient r₀:S₀ × S₁ ® S₀ et r₁:S₀ × S₁ ® S₁ les projections canoniques,
L=L₀ ×_* L₁={(a,*) / a Î L₀} È {(*,b) / b Î L₁} È {(a,b) / a Î L₀, b Î L₁} avec des projections canoniques p₀ et p₁,
(s,a,s') Î Tran_* ssi (r₀(s),p₀(a),r₀(s')) Î Tran_0* et (r₁(s),

p₁(a),r₁(s')) Î Tran_1*

Autres Constructions catégoriques

Le coproduit (``propriété universelle duale'' du produit cartésien) de deux systèmes de transitions T₀=(S₀,i₀,L₀,Tran₀) et T₁=(S₁,i₁,L₁,Tran₁) est T₀ Å T₁=(S,i,L,Tran) avec,

S=(S₀ È S₁)/{i₀=i₁), et i=i₀=i₁,
L=L₀ È L₁,
Tran=Tran₁ È Tran₂.

Produits Synchronisés

Un cas particulier: produit fibré suivant.

Référence plus générale: Arnold et M.Nivat.

Soient T₀=(S₀,i₀,L₀,Tran₀) et T₁=(S₁,i₁,L₁,Tran₁) deux systèmes de transition. Leur produit synchronisé (à la CSP) est T=(S,i,L,Tran) avec,

Définition

S=S₀ × S₁, i=(i₀,i₁),
L=L₀ × L₁,
((s,t),a,(u,v)) Î Tran ssi
- a Î L₀ Ç L₁ et (s,a,u) Î Tran₀ et (t,a,v) Î Tran₁,
- a Î L₀ \ L₁ et (s,a,u) Î Tran₀ et v=t,
- a Î L₁ \ L₀ et u=s et (t,a,v) Î Tran₁.

Sémantique de processus parallèles

Automate pour chaque processus séquentiel,
produit synchronisé correspondant aux différentes primitives de communications utilisées.

Les états globaux du système de transition résultant P sont donc des n-uplets (n=nombre de processus communicants) s=(s₁,...,s_n) avec s_i état local du processus P_i.

Jusqu'à une exponentielle de plus par rapport au cas séquentiel!

Dans le cas d'un langage proche de CCS, on pourra trouver dans [Winskel] une sémantique dénotationnelle, utilisant produits cartésiens, coproduits etc.

This document was translated from L^AT_EX by H^EV^EA.