TD 3-4. Introduction à CUDA
par Eric Goubault et Sylvie Putot
Utiliser CUDA dans les salles machines de l'X
On peut compiler les programmes comme dans le cours, à la ligne de commande, ou dans
un template de la SDK. On peut également tout faire depuis Eclipse (voir section suivante).
Compiler et exécuter un programme CUDA en utilisant Nsight Eclipse Edition
Le debugging
Est un problème toujours délicat avec CUDA. En premier lieu, utilisez cudaCheckErrors comme dans le cours. Ensuite, testez toujours petit à petit les noyaux, avec un nombre d'instance égal à un en premier lieu.
Si les bugs résistent, on peut utiliser le debugger de nsight, mais
pour ce faire, il faut avoir accès à deux cartes graphiques (une tournant sur CUDA, l'autre
faisant serveur X, pour nsight). C'est le cas parfois sur vos ordinateurs portables
(comme mon Mac) mais pas en salle TD. Pour pouvoir quand même utiliser nsight en mode
debugging il faut tricher un peu. Repérer et réserver d'abord une machine inutilisée en salle
TD (par exemple, allemagne dans ce qui suit). Nous demander ensuite pour que l'on
fasse la manip suivante:
[...] ssh -X eric.goubault@allemagne
Last login: Wed Jan 30 10:42:01 2013 from kelen.polytechnique.fr
[allemagne ~]$ who
eric.goubault pts/0 2013-01-30 10:42 (kelen.polytechnique.fr)
eric.goubault pts/1 2013-01-30 13:08 (kelen.polytechnique.fr)
[allemagne ~]$ sudo /sbin/telinit 3
(tue le serveur X d'allemagne)
Maintenant, c'est à vous:
[...] ssh -X allemagne
[allemagne ~]$ nsight &
Ainsi nsight va s'exécuter sur allemagne en utilisant votre machine
d'origine comme serveur X, et le code CUDA va être exécuté et débuggé sur allemagne.
La documentation
Une première mise en oeuvre : calcul de π en parallèle
Implémenter le calcul de π en parallèle avec la formule suivante (cf aussi le TD1) :
\[ \pi = \int_0^1 \frac{4}{1+x^2} dx \approx \sum_{i=1}^n \frac{1}{n} \frac{4}{1+((i-\frac{1}{2})\frac{1}{n})^2}. \]
Principe général de calcul
Une solution est le paradigme Maître/Esclave.
Un maître va lancer N esclaves chargés de calculer les sommes
partielles
\[ P_k = \sum_{i=(k*n)/N+1}^{((k+1)*n)/N} \frac{1}{n} \frac{4}{1+((i-\frac{1}{2})\frac{1}{n})^2} \, , \; k=0,\ldots,N-1, \]
puis faire la somme des résultats partiels.
Quelques pistes et suggestions pour l'implémentation CUDA
Vérification des résultats et affichage des performances
- Comparer le résultat obtenu sur GPU avec le calcul de Pi pour la même valeur de n
- Ajouter des mesures des temps de calcul et afficher l'accélération par rapport au programme séquentiel;
plusieurs solutions pour mesurer le temps de calcul:
- Ne pas hésiter à récupérer les messages d'erreur éventuels en utilisant les fonctions checkCudaErrors/getLastCudaError(attention sinon, l'exécutable peut très bien s'être planté sans rien dire...) ; pour les problèmes d'accès mémoire (voire pour avoir plus d'info sur ce qui est réellement calculé),
vous pouver utiliser cuda_memcheck (compiler avec -g -G)
Précision des calculs
- Si les calculs sont effectués en simple précision et si on prend n trop grand, un phénomène d'absorption fait que la précision des résultats devient mauvaise,
- Si vous n'utilisez pas nsight, avec les options de compilation par défaut, les double sont interprétés sur le GPU comme des float, appelez donc nvcc avec l'option -arch=sm_13. Attention aussi, avec l'option -arch=sm_13, seuls les unités double seront utilisées, même si votre programme
utilise des float et non des double
Faire varier taille des grilles et des blocs
Faire varier n, le nombre de blocs, de threads par blocs et observer les performances relatives.
Le Hello World! de CUDA : produit matriciel
On s'intéresse à l'implémentation du produit matriciel \( C = A \cdot B \) des deux matrices \(A\) et \(B\).
\[
A = \left(a_{i,j}\right)_{0\leq i < n , 0 \leq j < m}
= \frac{i}{j+1}
\qquad \qquad
B = \left(b_{j,l}\right)_{0 \leq j < m, 0 \leq l < k}
= \frac{l}{j+1}
\]
Version simple
Implémentez le produit matriciel en utilisant un thread pour chaque entrée \(c_{i,j}\).
Version utilisant la mémoire partagée
Nous voulons à présent améliorer la performance en utilisant la mémoire partagée.
L'idée centrale est illustrée dans l'image suivante.
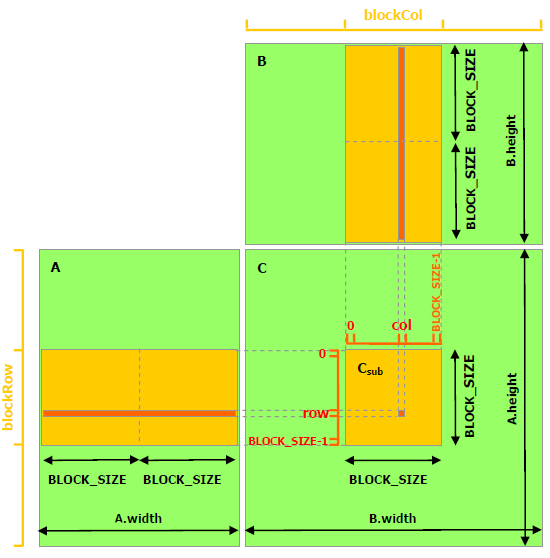
Une matrice
\(D = (d_{i,j})_{0 \leq i < n, 0 \leq j < m}\)
est découpée en sous-matrices
\(D_{\rm sub}^{u,v} = (d^{u,v}_{l,k})_{0 \leq l < {\rm BS}, 0 \leq k < {\rm BS}} \) ;
alors, on a \( d^{u,v}_{l,k} = d_{(u * {\rm BS} +l),(v * {\rm BS} +k)}\).
Chaque sous-matrice \(D_{\rm sub}^{u,v} \) peut résider dans la mémoire partagée d'un bloc.
Écrire un kernel pour calculer la matrice \(C\) en utilisant la mémoire partagée,
en utilisant un thread pour chaque entrée \(c_{i,j}\) de la matrice \(C\), et un bloc de threads pour chaque sous-matrice \(C_{\rm sub}\).
Rappelons que les grids et blocks sont organisés dans la manière suivante.
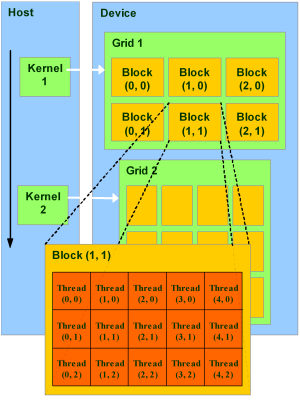
Pour ça, il est naturel de prendre \( u = \tt blockIdx.y =: by \), \( v = \tt blockIdx.x =: bx\),
\(l = \tt threadIdx.y =: ty \), \(k = \tt threadIdx.x =: tx\).
Le thread \(\tt(tx,ty)\) dans le block \(\tt (bx, by)\) calcule alors
\[ c^{\tt by,bx}_{\tt ty, tx} = c^{u,v}_{l,k} = c_{(u * {\rm BS} +l),(v * {\rm BS} +k)} = c_{({\tt by} * {\rm BS} +{\tt ty}),({\tt bx} * {\rm BS} + {\tt tx})}. \]
Simulation différences finies
Equation de Laplace
Nous voulons calculer la distribution de température dans une pièce carrée, sachant que la température sur les bords est fixée: la température sur les murs de la pièce est de 20 degrés, sauf sur l'un des murs (disons la cheminée...), ou elle est à 100 degrés.
En régime stationnaire, c'est-à-dire lorsque la température est stabilisée, la température vérifie l'équation de Laplace (bi-dimensionnelle ici) \[ \Delta T = \frac{\partial^2 T}{\partial x^2} + \frac{\partial^2 T}{\partial y^2}= 0.\]
Nous allons calculer la température sur une grille régulière par une méthode de différences finies classique,
en approchant les dérivées partielles au point (x,y) par
\[ \frac{\partial^2 T}{\partial x^2}(x,y) \approx \frac{1}{h^2} (T(x+h,y) - 2 T(x,y) + T(x-h,y) ), \]
\[ \frac{\partial^2 T}{\partial y^2}(x,y) \approx \frac{1}{h^2} (T(x,y+h) - 2 T(x,y) + T(x,y-h) ), \]
ou h est un pas de discrétisation suffisamment petit. En supposant qu'on a discrétisé le rectangle par une grille de N par N
points, alors la température en chaque point (i,j) de la grille peut
s'exprimer directement en fonction de ses voisins immédiats, par
\[ T_{i,j} = \frac{T_{i-1,j}+T_{i+1,j}+T_{i,j-1}+T_{i,j+1}}{4}, \; \forall i,j \in \{1,\ldots,N-2\}, \]
les températures pour i=0, i=N-1, j=0 et j=N-1 étant données par les conditions limites.
Calcul séquentiel de la température en chaque point
Pour calculer la température en chaque point, on va donc itérer ce calcul jusqu'à ce que la différence entre deux itérées successives devienne inférieure à un certain seuil. On va dans un premier temps implémenter la version de référence séquentielle et afficher les résultats.
Vous pouvez faire plusieurs versions:
- une première, la plus simple, qui pour un nombre d'itérations n fixé, calcule par l'itération de Jacobi:
\[ T^{k+1}_{i,j} = \frac{T^k_{i-1,j}+T^k_{i+1,j}+T^k_{i,j-1}+T^k_{i,j+1}}{4}, \; \forall i,j \in \{1,\ldots,N-2\},\; \forall k \in \{0,\ldots,n\}\]
et qui sera celle à implémenter sur le GPU dans un premier temps, car elle est naturellement parallélisable;
- une deuxième qui utilise une itération de Gauss-Seidel: on utilise les valeurs nouvellement calculées (donc pour le même k) pour accélérer la convergence de la méthode; elle sera la version séquentielle de réference pour
calculer l'accélération due à l'utilisation du GPU;
- enfin, on modifiera chacune de ces deux versions pour s'arrêter non plus après un nombre fixé d'itérations, mais lorsque le calcul a convergé (la différence max entre la température aux pas k et k+1 est inférieure à un seuil donné)
Une possibilité pour l'affichage
Pour l'affichage des résultats, vous pouvez par exemple:
- insérer votre code dans le fichier suivant chaleur.cu, en mettant également les fichiers pixmap_io.h et pixmap_io.cdans le répertoire; la fonction main vous montre comment afficher le tableau T;
- l'exécution produit un fichier de résultats out.pnm, que vous pouvez afficher par exemple par gimp out.pnm (ou bien, en salle machine, simplement en double cliquant sur le fichier)
- dans un second temps, pour éventuellement visualiser l'évolution de la température au cours du temps, dans le cas de l'équation de la chaleur,
vous pourrez sauver plusieurs fichiers à différents instants et utiliser ImageMagick pour l'affichage
Versions parallèles
- Implémenter et comparer les performances en temps de calcul des versions parallèles suivantes de l'algo précédent:
- Version pour un nombre fixé d'itérations, et dans laquelle tous les threads sont synchronisés (par le CPU)
à chaque itération k, version couteuse, qui nécessite de relancer un "kernel" à chaque itération
- Si on relache la contrainte de synchronisation, on se retrouve avec une itération de style Gauss-Seidl beaucoup plus efficace mais suivant les cas elle peut ne pas converger, expérimenter des versions de ce type
- Version avec critère d'arrêt sur la convergence du calcul, et non plus nombre d'itérations fixé: comment faire efficacement et correct?
Quelques suggestions:
- Pour chaque version, bien vérifier que les résultats sont bien comparables sur GPU et CPU, et comparer les temps d'exécution lorsque l'on fait varier les tailles des blocs et grilles, ainsi que le nombre de points N de discrétisation,
- Vous pouvez essayer de tirer parti de la mémoire shared, des fonctions atomic
Equation de la chaleur
On s'intéresse maintenant à l'évolution de la température dans la pièce, modélisée par l'équation de la chaleur
\[ \frac{\partial T}{\partial t} = \alpha \Delta T, \]
en partant par exemple d'une température égale à 20 degrés partout sauf sur un mur ou elle est égale à 100,
et avec comme conditions aux limites 20 degrés sur tous les murs sauf celui ou elle vaut 100.
Calculer la température en fonction du temps par une méthode de différences finies. Cette fois, la
synchronisation stricte est nécessaire. Comme précédemment, implémenter et comparer plusieurs versions
en essayant d'améliorer progressivement les performances:
- synchronisation par le CPU comme précédemment,
- synchronisation par blocs et inter blocs en utilisant les fonctions atomic,
- mémoire shared

