Informatique -- Tronc Commun
TD 8 - Graphes: Chemins dans un labyrinthe, Algorithme de Dijsktra
Benjamin Werner, Eric Schost
10 janvier 2000
Objet
On continue à manipuler des graphes. Aujourd'hui, le but sera de
trouver des chemins entre deux sommets d'un graphe. Pour rendre la
chose plus attrayante, on présentera cela comme trouver la sortie d'un
labyrinthe.
On fournit la définition des graphes/labyrinthes et quelques outils
pour les afficher. Normalement ils doivent être assez faciles à
utiliser et à comprendre.
D'abord, on cherchera à trouver un chemin quelconque pour sortir du
labyrinthe. Ensuite, on cherchera à trouver le chemin le plus court.
1 Labyrinthes
Les labyrinthes sont dessinées sur un damier de taille n× m.
C'est donc un graphe non-orienté dont les sommets sont les
couples (i,j) avec 0£ i < n et 0£ j < m.
Les sommets sont définis dans la classe
Sommet.java.
Ensuite, un labyrinthe est un tableau où chaque sommet est associé à
la liste de ses voisins. Les listes de sommets sont définies de
manière habituelle dans
ListeSommets.java. Un labyrinthe est donc un
tableau de listes de sommets, avec deux entrées i et j. Plus
exactement, la classe Laby contient les champs suivant:
-
le tableau de listes de sommets voisins,
- ses dimensions hauteur et largeur,
- les deux sommets entree et sortie.
C'est défini au début de Laby.java, avec ensuite un certain
nombre de fonctions qui servent à lire un labyrinthe et qu'il n'est
pas nécessaire de regarder.
Remarquez que cette définition permet de représenter des graphes
orientés. Ici si s1 est voisin de s2, alors s2 le sera aussi de s1.
2 Affichage
On fournit également de quoi afficher un labyrinthe. C'est défini dans
la classe AnimLaby.java, et la première fonction est AnimLaby.start qui ouvre la fenêtre graphique et affiche le
labyrinthe passe en argument.
Pour essayer, récupérez les fichiers Sommet.java,
ListeSommets.java, Laby.java, AnimLaby.java et Demo.java. Regardez
ce dernier pour découvrir les fonctions à utiliser:
-
AnimLaby.start qui affiche un labyrinthe,
- AnimLaby.fleche(Sommet s, Sommet t) qui affiche la flèche
de s vers t, à condition que ces deux sommets soient voisins. Un
deuxième appel avec les mêmes arguments efface la flèche.
- AnimLaby.pause(int i) temporise pendant i millièmes de
seconde.
Deux définitions de labyrinthes sont données dans les fichiers
petit.laby et grand.laby. Pour s'en servir, compilez
les fichiers java, puis faites:
java Demo < petit.laby
Cette manipulation fait que le labyrinthe décrit dans petit.laby
est chargé dans la variable laby.
Vous devez voir une fleche clignoter.
3 Sortir à tout prix
Le premier travail demandé, est de trouver un chemin pour sortir du
labyrinthe. On utilise la méthode la plus simple, quitte à ne pas
prendre le chemin le plus court: c'est une exploration en
profondeur d'abord.
Concrètement, on se trouve sur un sommet donné. On choisit le premier
voisin venu et on recommence. Si à un moment donné il n'y a plus de
voisin, cette branche de l'exploration a échoué et on remonte essayer
une autre branche.
On s'arrète bien sûr quand on arrive sur la sortie.
Ca se programme simplement en utilisant la récursivité (une
quinzaine de lignes).
Le plus simple est d'utiliser une fonction booléenne qui répond si
elle a déjà trouvé la sortie ou pas. On aura besoin d'un tableau de
booléen indiquant si l'on a déjà visité un sommet ou pas.
Pour animer, on affiche une flèche quand on explore un chemin. On
l'efface quand on revient. Voila ce que cela peut donner:
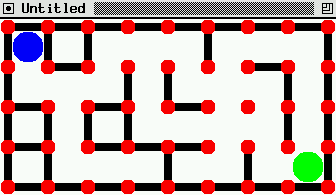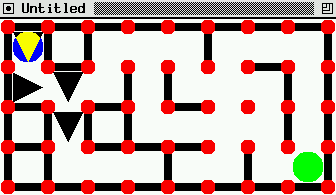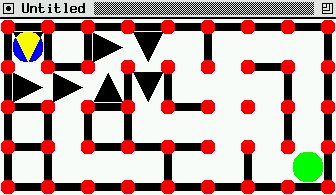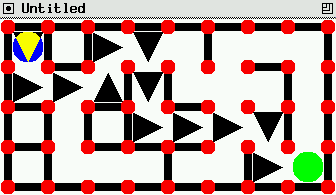
Cliquez sur
Stop pour interrompre, sur
Reload pour
reprendre.
Voici une solution.
4 Trouver le plus court chemin
On veut maintenant trouver le plus court chemin. Pour cela, on va
faire une exploration en largeur d'abord.
Il s'agit en fait de construire un arbre. La racine de l'arbre est
l'entrée du labyrinthe. A chaque étape, on ajoute tous les voisins de
chaque feuille à l'arbre. Lorsque l'on tombe sur la sortie, c'est
fini.
A chaque étape, il faut construire la liste des sommets qu'il faudra
visiter à l'étape suivante. Si on veut juste calculer la longueur du
plus court chemin, cela suffit: il n'est pas nécessaire de construire
l'arbre.
Si on veut afficher le chemin de sortie, il faut en revanche
construire l'arbre.
Le plus simple est de représenter l'arbre sous forme de tableau, ou
chaque sommet pointe vers son père. Lorsqu'il n'y a pas encore de
père, on choisira une valeur spéciale, par exemple (-1,-1).
On se propose de construire l'arbre en affichant au fur-et-à mesure
les flèches correspondantes. Une fois le chemin trouvé, on peut faire
clignoter les flèches qui en font partie (c'est-à-dire la flèche entre
la sortie et son père, puis de son père vers le grand-père, etc).
Voici une solution.
This document was translated from LATEX by HEVEA.

