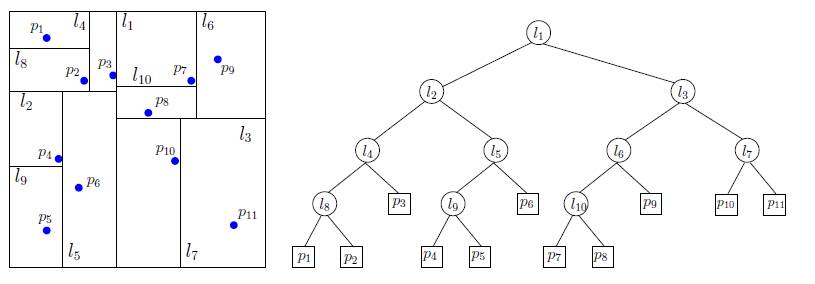
TD 3 - Kd-trees and their applications


Introduction:

The goal of this practical session is to implement and test some algorithms and data structures for geometric proximity problems in dimension 2. For the sake of simplicity, we provide a few methods and data structures for dealing with point sets integer grids.

Files to download today:

How to solve this practical TD


Today you are provided with the following classes (overview)


Data structures for point clouds
 FastRangeSearch, SlowRangeSearch fast and slow implementations of the RangeSearch interface


LinkedList (storing integer 2D points, type GridPoint)
 a linkedlist representation of a point cloud (in arbitrary dimension)

CoordinateComparator
 A comparator for points, allowing us to compare the values of the i-th coordinate of two points
(useful for sorting arrays of points, using the method: Arrays.sort())




Files to be completed
 KdTreeNode (exercise 1)
 Implementation of a Kd-Tree and the computation of closest neighbors





Files for testing your code
 TestKdTree (exercise 1)
 Check the correctness of the construction of the Kd-Tree

TestRangeSearch Test the correctness of the range search queries


Pipeline: complete the provided classes

For each exercise you will be asked to complete the skeleton of a class and to execute the provided test programs. More precisely, you will have to solve the questions below:

Exercise 1: file KdTree.java

1. Construction and implementation of Kd-trees

You will have to complete the class KdTree: as illustrated during the lecture, kD-trees provide an efficient solution for anwering proximity queries, such as "range search queries".

Task 1: Recursive construction:
The construction of the kD-tree (a binary tree) can be performed by recursively partitioning the input point cloud N using separating hyperplanes. kD-trees are defined as follows:
  • each node represents a D-dimensional box (hyper-rectangle) and is associated with the following informations:
    • lthe point cloud lying in the box (represented by the class PointCloud)
    • the geometric informations concerning the cut: the direction, and the position (by default defined by the location of the median point, along the given cut direction)
  • the leaves contain isolated points (PointCloud of length 1)
  • the root node is associated to the entire input point cloud N.
  • for each node in the tree its descendant nodes correspond to the two D-dimensional boxes obtained by cutting with the separator hyperplane: by construction separator hyperplanes are parallel to the coordinate axes.
Task 2: Computing closest neighbors (of a given point) at distance at most R
The computation of the closests neighbors q (within a given distance), can be performed recursively using a tree traversal (from the root node). At each step you have to check whether the disk centered at q of radius R is intersecting the separator hyperplane:
  • if the disk intersects the separator hyperplane then you must perform recursively the search in the two descendant nodes (left and right children): the result of this query will be the union of the results of the two queries performed on the descendant nodes
  • If there is no intersection (between the disk and the hyperplane) then it means that the search must be performed only on one sub-tree, the one whose root node corresponds to the box containing the query point q): in this case you have to check whether the disk is lying on the left or on the right of the separating hyperplane.



(example of a 2D-Tree decomposition)

1.1 Computing the separating hyperplane

The choice of the separating hyperplane (parallel to the coordinate axes) can be done in several ways (see the 2 methods suggested below). The direction of the separating hyperplane will be denoted by a field cutDim: for point clouds in dimension d the field cutDim takes values 0 ... d-1.

For the computation of the median we first sort the points along the cut direction.
Computing the median value can be performed via the class MedianWithSorting.
Splitting the point cloud around the median is already implemented in the class PointSetUtil.



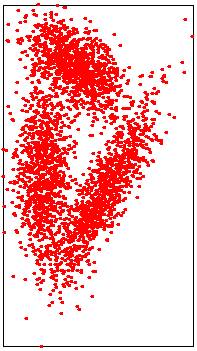
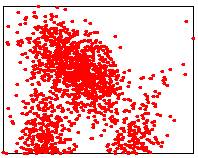
Input point cloud
 Exact median: sorting points in O(n log n) time

Lower points: 1500/3000



1.2 Construction of the Kd-Tree

Now it remains to perform the recursive construction of a kD-tree storing the input point cloud as described above. Complete the constructor
that takes as input:

Hint: here is a sketch of the solution
Input: N, cutDim


    Initialize the data stored in a KdTree node: cutDim, points, numPoints


    Compute the cutValue, either using the median or the barycenter.


    Given a point cloud N 

    - create two point clouds lowerN and upperN: they provides a partition of N, corresponding to the points which are smaller (or greater) of the cutValue (according to the cut direction)


    Check whether the two subsets of points are empty or not

    - if these subsets are not empty than proceed recursively and create two sub-tree (warning: the cut direction should be modified accordingly)


    - otherwise, if both the subsets are empty, return null (we reach a leaf of the Kd-Tree)

To test your code use the class TestKdTree.
-) run the class TestKdTree without any argument to generate 1000 random points in 2D
-) run TestKdTree data/2D_dataset1.dat to read the point cloud from an input file

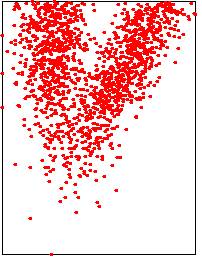
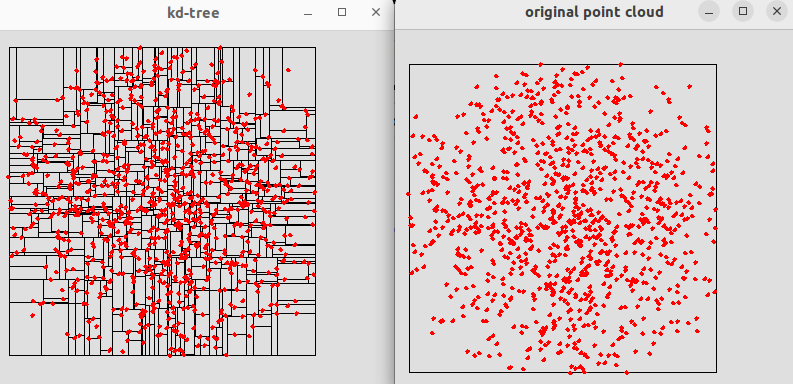
Here is the result (for 1000 random points): 
Exercise 1.2: testing Kd-trees construction
Generating 2D point set in disk...done (1000 points)
Checking correctness of the Kd-Tree:
	 size original point cloud: 1000
	 size Kd-Tree (total number of nodes): 1999
	 number of leaves in the tree: 1000
test done.


KdTree (2D) of 1000 random points
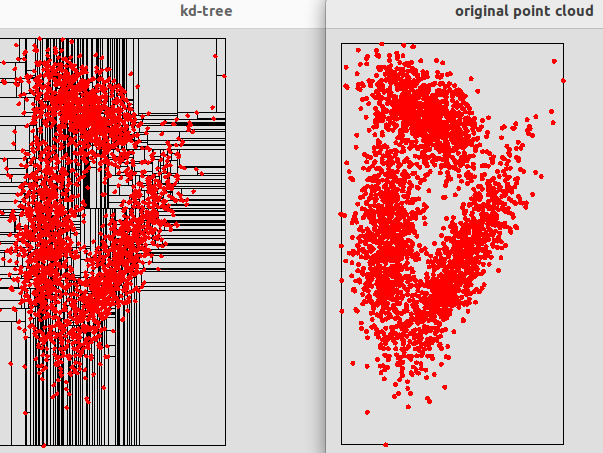
KdTree (2D) corresponding to the input file 2D_dataset1.dat



1.3 Range Search

It remains to complete the method below which recursively computes the points at distance at most sqRad from a given query point q.
Input:


To test your code you can run the class TestRangeSearch


 
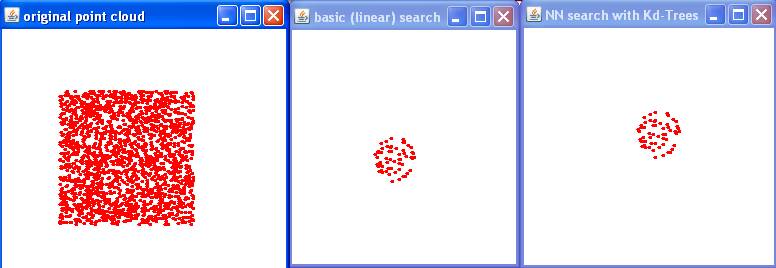
            Exo 1.3: testing Range Search
Generating 2D point set in disk...done (200000 points)
Generated 2D point set in unit square (10000 points)
Initializing Kd-Tree data structure...  done
Checking correctness: "Brute-force search" versus "Fast Kd-Tree search"...ok (0 neighbors)

Running benchmark for Brute-force search...done
	 elapsed time: 34478 ms (time per query: 3.4478 ms)
	 number of query points: 10000
Running benchmark for Fast Kd-Tree search...done
	 elapsed time: 2093 ms (time per query: 0.2093 ms)
	 number of query points: 10000
test done.
Range Search performaces:
Total construction time: 1s 955ms
Total NN query time: 0s 0ms



Here is the result obtained running the class RangeSearch (with 200k input points in 2D and 10k queries)
    Exo 1.3: testing Range Search
Generating 2D point set in disk...done (200000 points)
Generated 2D point set in unit square (10000 points)
Initializing Kd-Tree data structure...  done
Checking correctness: "Brute-force search" versus "Fast Kd-Tree search"...ok (0 neighbors)

Running benchmark for Brute-force search...done
	 elapsed time: 34478 ms (time per query: 3.4478 ms)
	 number of query points: 10000
Running benchmark for Fast Kd-Tree search...done
	 elapsed time: 2093 ms (time per query: 0.2093 ms)
	 number of query points: 10000
test done.
Range Search performaces:
Total construction time: 1s 955ms
Total NN query time: 0s 0ms
To test 3D Data you can run the class TestIO with input file: 3D_nefertiti.dat 

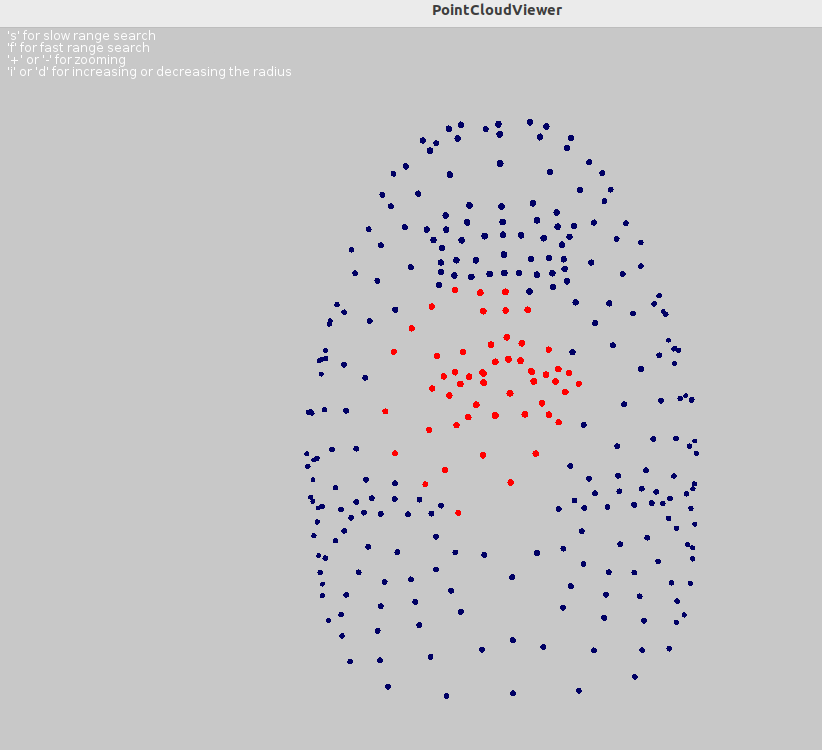
Loading point cloud from data: data/3D_nefertiti.dat
Loading point cloud from file data/3D_nefertiti.dat ... done
Drawing point cloud in 3D...Point cloud: 299 points
Space dimension: 3
Closest neighbors at distance r=1.0: 32
Closest neighbors at distance r=1.0: 54