TD 1 - 2D triangle meshes

Planar Point location

Now we will become familiar with more structured geometric objects, such as meshes. In particular, the goal of this section is to illustrate the functionality of the Polyhedron_3 class, which allows for the representation of surface meshes (orientable).

From a combinatorial perspective, a combinatorial surface of genus 0 corresponds to a planar graph: this is also why the Polyhedron_3 class is a generic class, parameterized by the type of point you want to associate with the mesh vertices, which in Java is expressed as:

Polyhedron_3<X extends Point_>

Point location and random walks

Here, you are asked to implement the point-location algorithm in a planar triangulation based on a random walk (see the explanatory slide). We start from a point q chosen at random in the triangulation and trace the segment (pq), where p is the point to be located.

Task: Write a program that allows you to locate p in the triangulation.

Output of the location method: a half-edge belonging to the face that contains p.

Once again, we provide you with the skeleton of the PointLocation_RandomWalk class in the file, which contains the method signatures to complete, as well as a main function that allows you to test your code (once written).

Files to download and documentation for this exercise:

Datasets for testing your code: Delaunay triangulations stored in OFF format (a smaller one and a large one). Warning: do not forget to place these datasets in the /data folder (at the root of projet TD1)
The skeleton to complete: PointLocationInTriangulations.java.
The class for testing: TestPointLocation.java.

Testing your code:

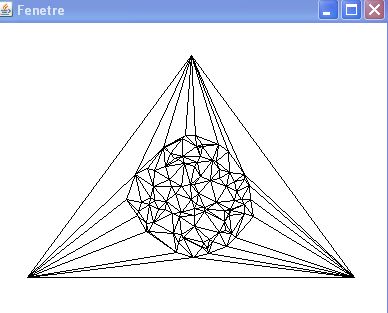
Run the class TestPointLocation: you should see a 2D window showing the input triangulation, as below:

...
...
Checking Polyhedron...ok
Closed mesh: no boundaries
The mesh is pure triangle
n: 103  e: 303  f: 202 - genus: 0
Checking Polyhedron...ok
Mesh with boundaries
The mesh is pure triangle
n: 103  e: 303  f: 201 - genus: 0
Exception in thread "main" java.lang.Error: a completer
	at PointLocation_RandomWalk.getRandomPoint(PointLocation_RandomWalk.java:30)
	at PointLocation_RandomWalk.main(PointLocation_RandomWalk.java:99)

Tip: here are some of the classes and methods you will need for this exercise:

Point_2 (in the Jcg.geometry package): implements functions necessary to manipulate 2D points (with real, double-precision coordinates).
Fenetre: for visualizing a set of points and segments.
GeometricOperations_2 (in Jcg.geometry): provides a number of geometric predicates (for example, a predicate to test the orientation of a triangle).

In the TestPointLocation.java file, there is also a method to load a planar triangulation into memory in order to test your code.

Tip: you can approach this exercise step by step by completing the different functions provided in the .java file above.