



















The goal of this lab session is to use persistent homology to explore a database of images.
We want to explore the Columbia University Image Library. It is composed of a collection of 1440 grayscaled images, 128x128 pixels each. These images were obtained by taking pictures of physical objects from various angles. More precisely, there were 20 objects, and each object was photographed 72 times while turning around it, giving one picture every 5 degrees. Then, the background has been removed and the images have been rescaled (see the examples below). Our goal is not so much to distinguish between the 20 objects (which is relatively easy), but rather to get insights into the acquisition process and the ways in which it interacts with the objects' intrinsic symmetries.





|





|





|





|
Here are the images. For the purpose of the session, the images have been preprocessed as follows:
The 20 matrices are provided here. Once again, there is one matrix per object, which contains the coordinates of the corresponding point cloud with 72 points in 16384 dimensions.
First we will use dimensionality reduction to visualize the data.
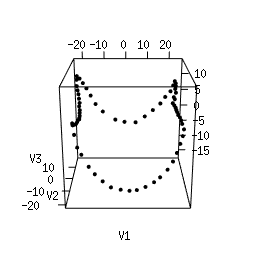
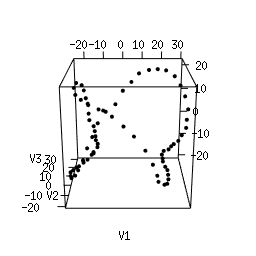
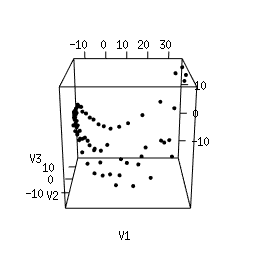
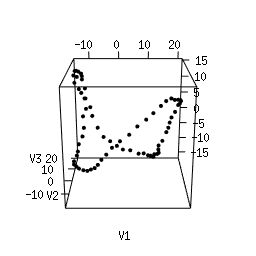
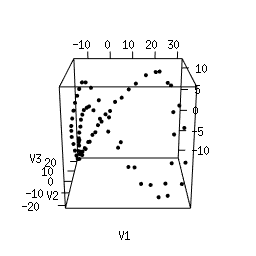
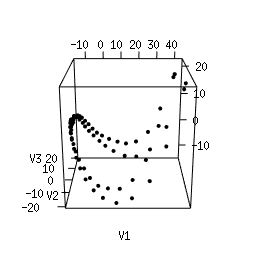
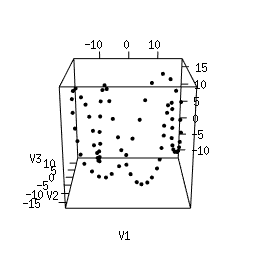
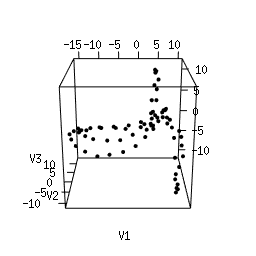
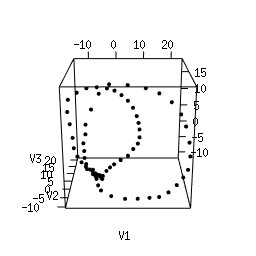
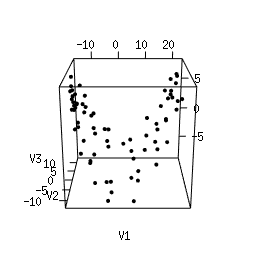
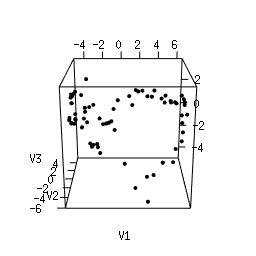
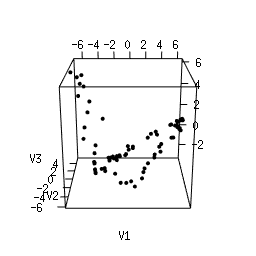
Q1. Use Multi-Dimensional Scaling (MDS) to compute an as-faithful-as-possible embedding of the data into R^3. You can do it in Python using manifold.MDS from the Scikit-Learn library. Alternatively, you can do it in the R language using the following code. Plotting the resulting 3d point clouds should give you the following plots, which we have arranged in the same way as the images above (click on a plot to see a close-up):
|
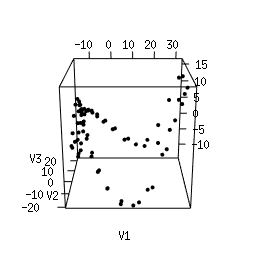
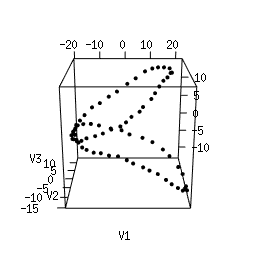
|
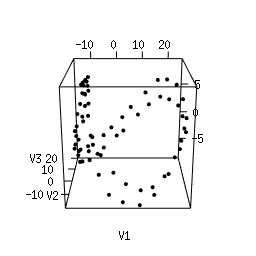
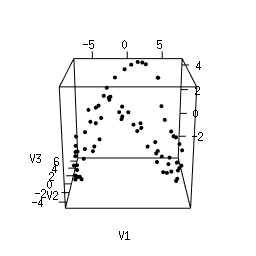
|
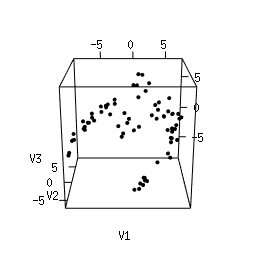
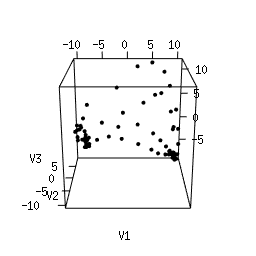
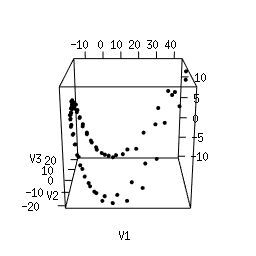
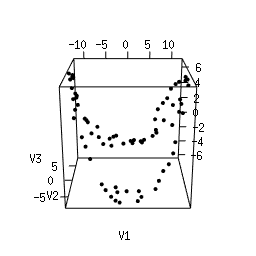
|
Q2. Compare each 3d plot against the images of its
corresponding object. Can you relate the presence of loops in the
cloud to the acquisition process and the symmetries of the
object?
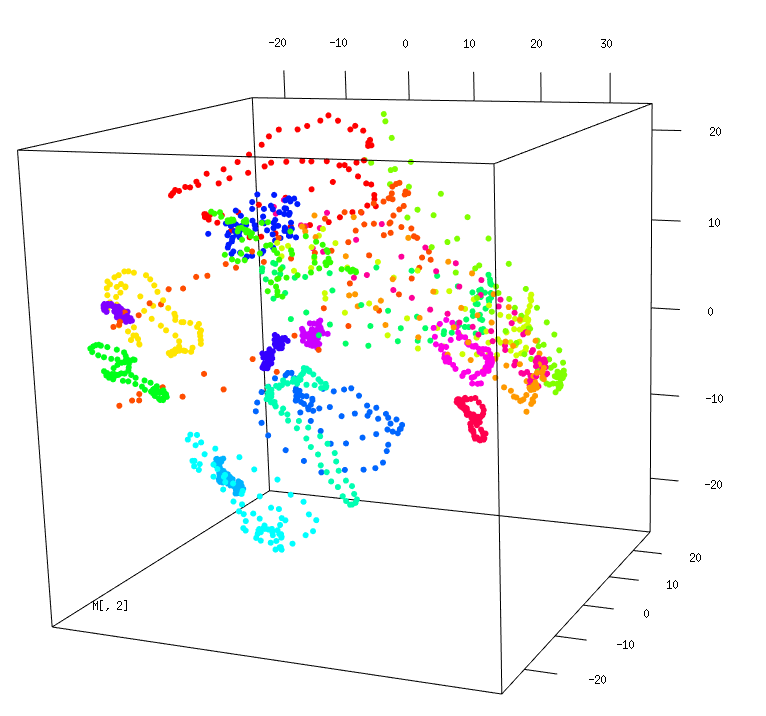
Note: To help you in this task, you can also concatenate
the 16384-dimensional clouds into a single one, then apply MDS to it
(is this equivalent to concatenating the 3-dimensional clouds
directly? why?) and plot the result with colors corresponding to the
different objects, as illustrated below. This should give you a better
sense of the relative sizes of the loops coming from the various
objects. Here is our solution code in
R.
Now we want to confirm or infirm the presence of loops in the 16384-dimensional clouds using topological inference. This will allow us to refine our insights from section 1.
Q3. Compute the vertices, edges and triangles of the full Rips filtration of each cloud. To minimize the amount of work, you can take advantage of the following observations:
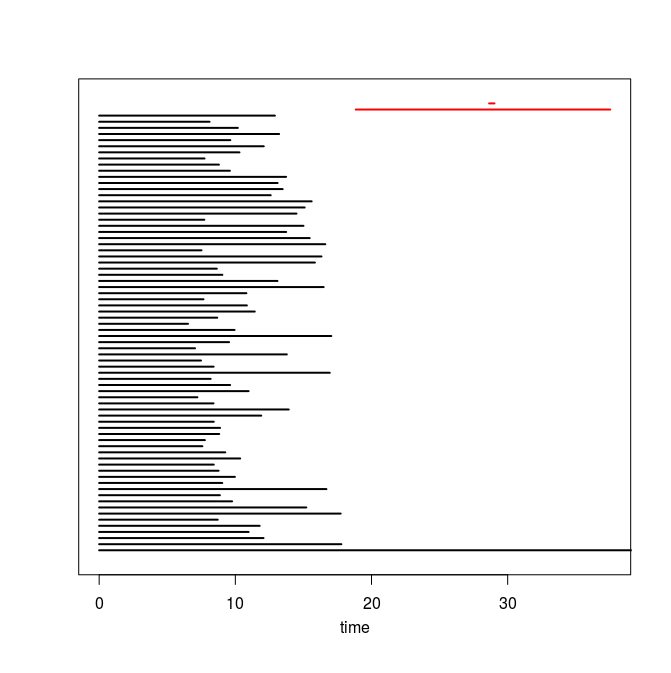
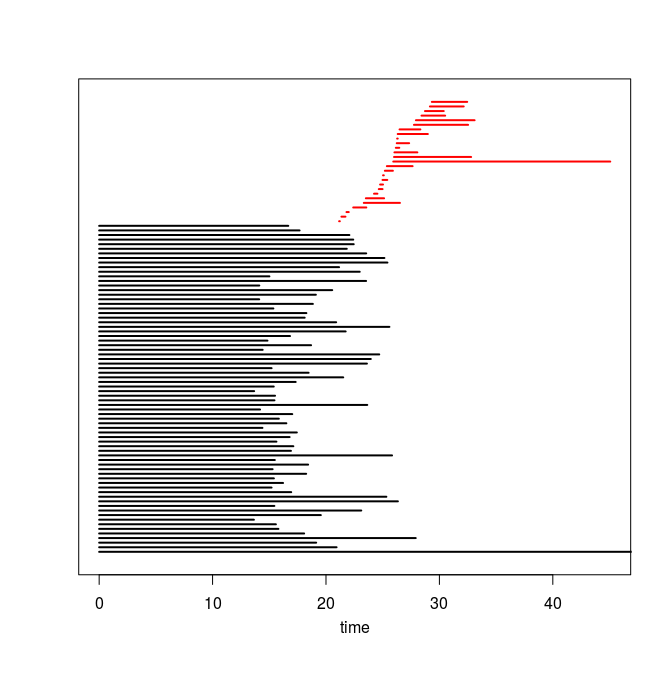
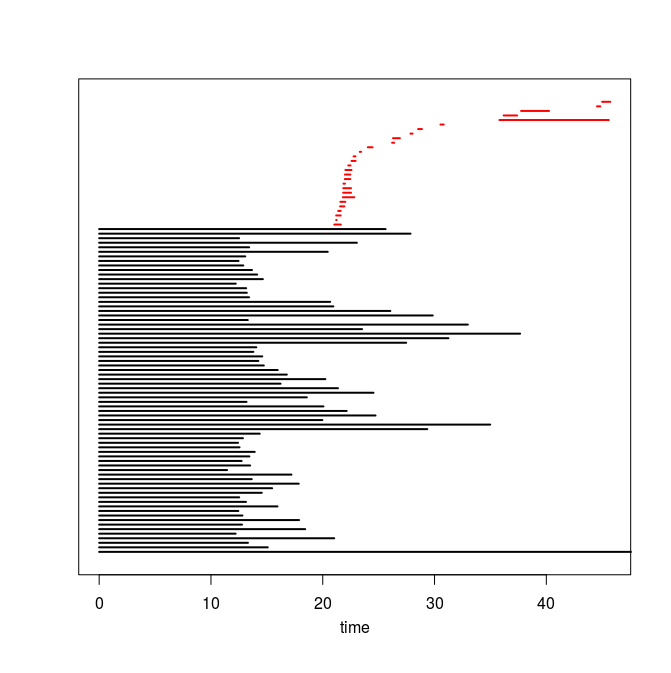
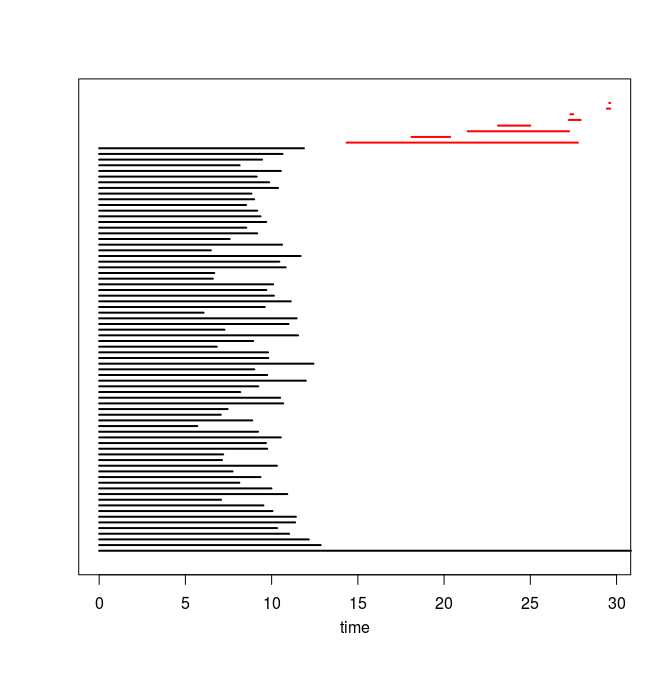
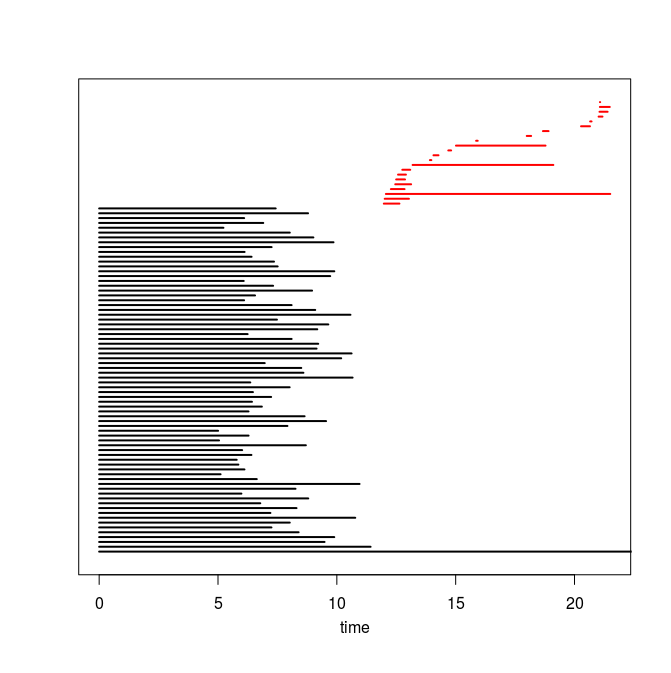
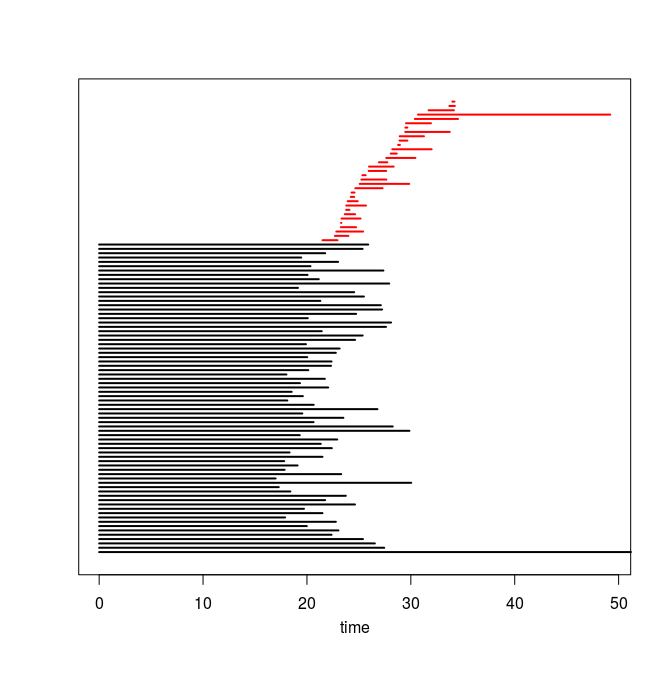
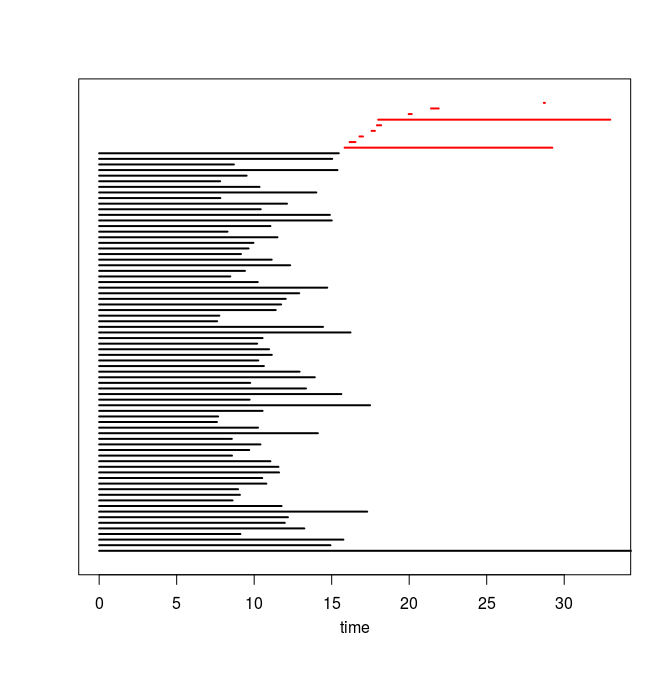
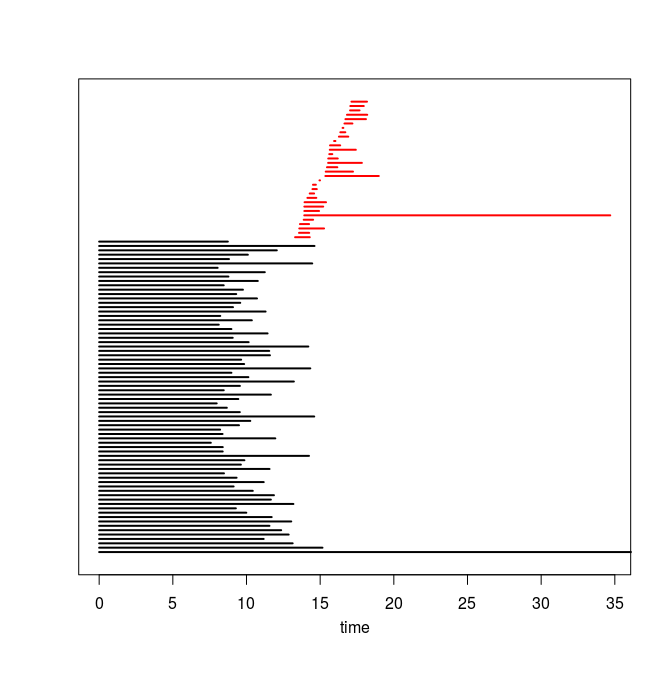
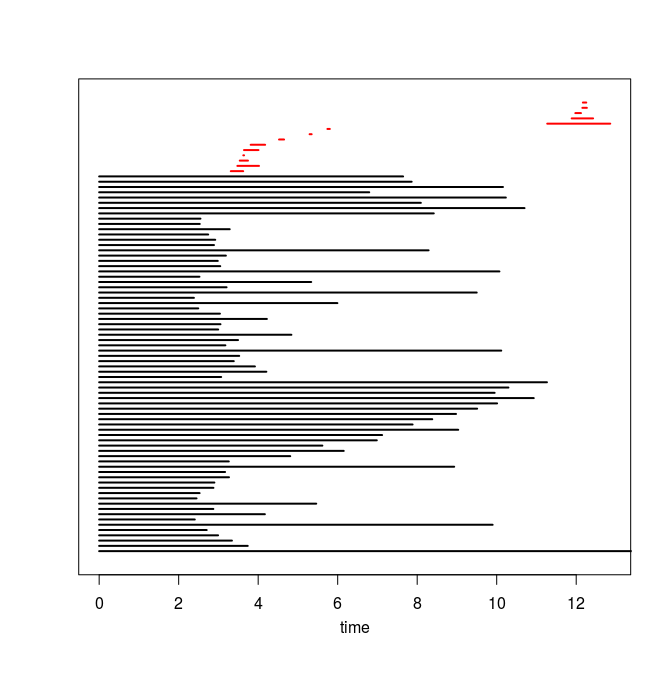
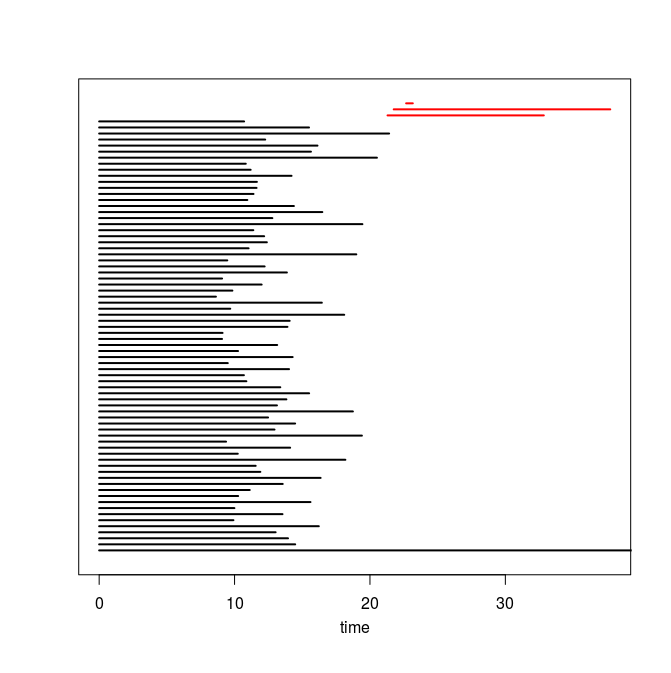
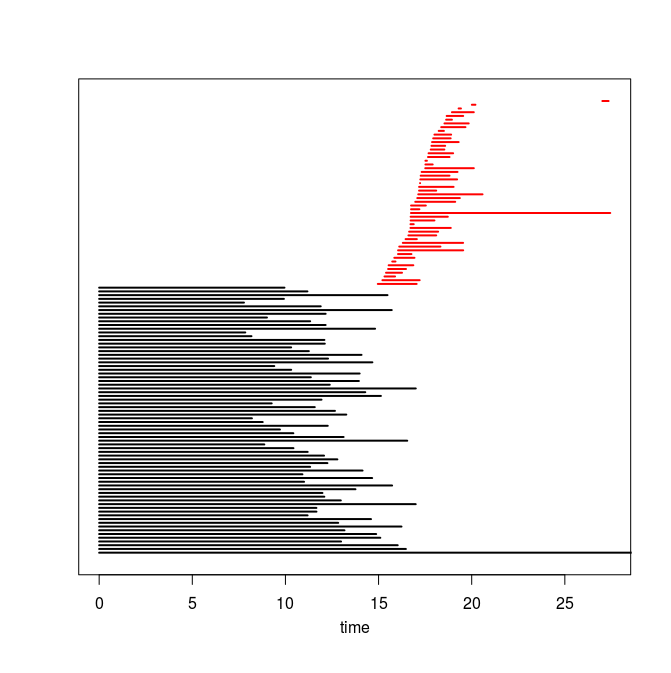
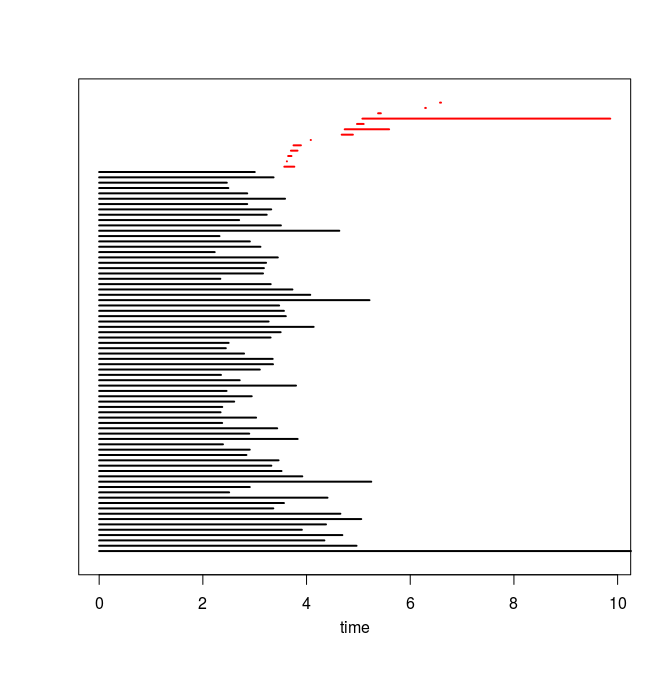
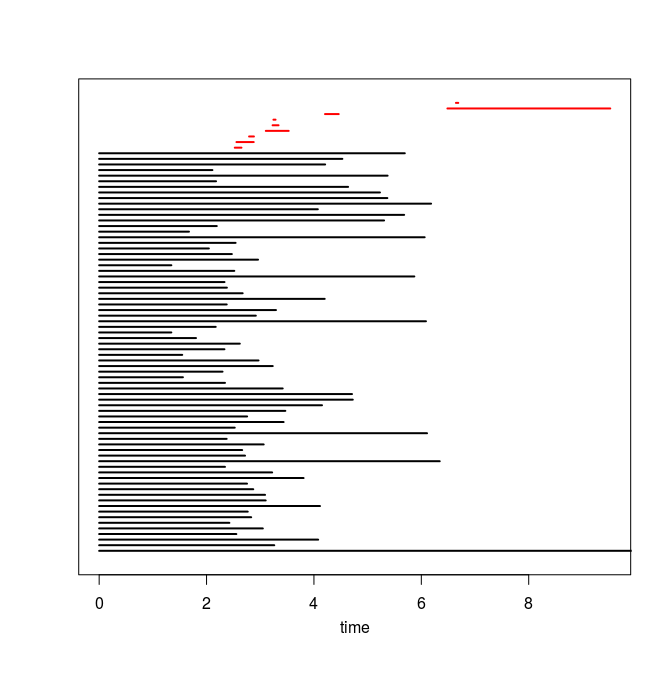
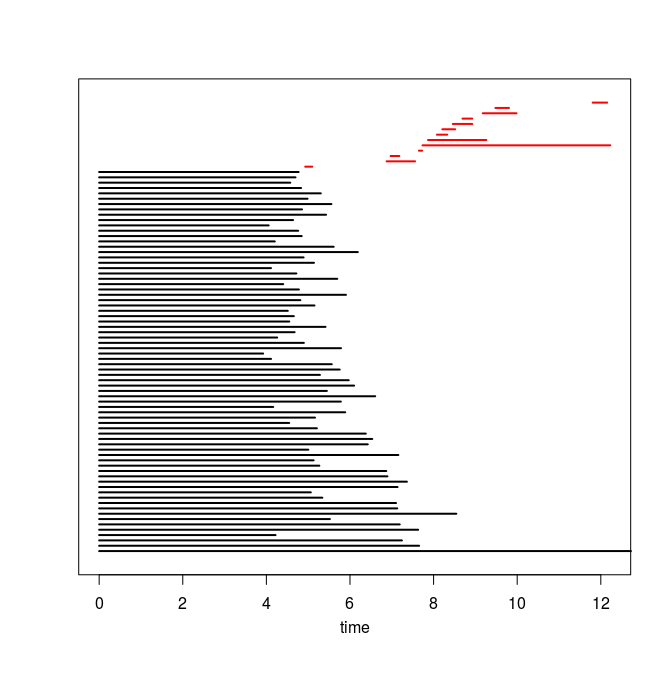
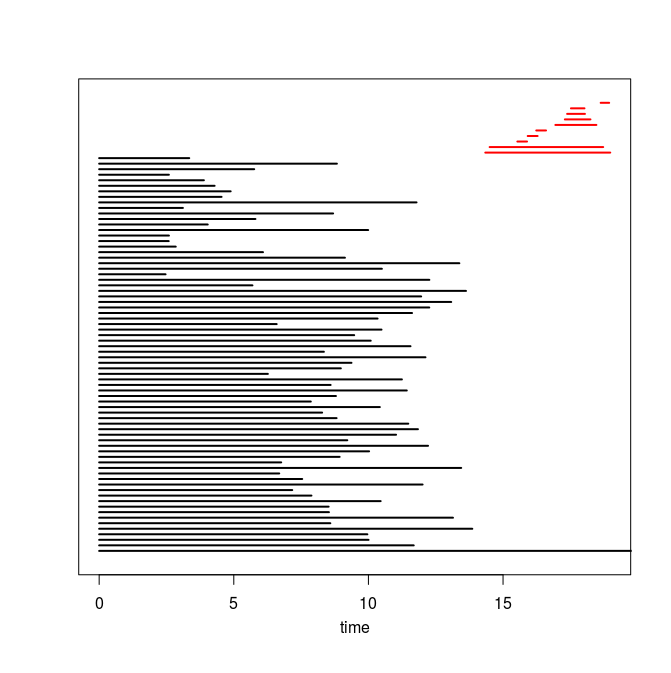
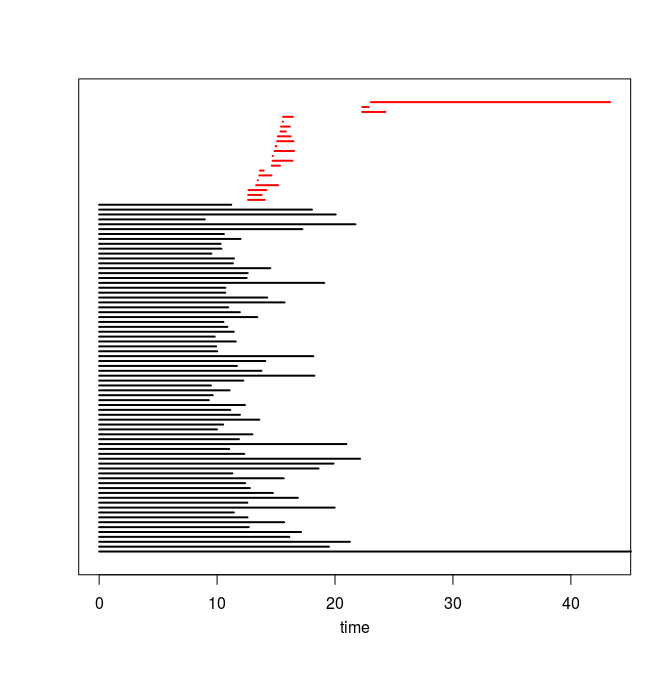
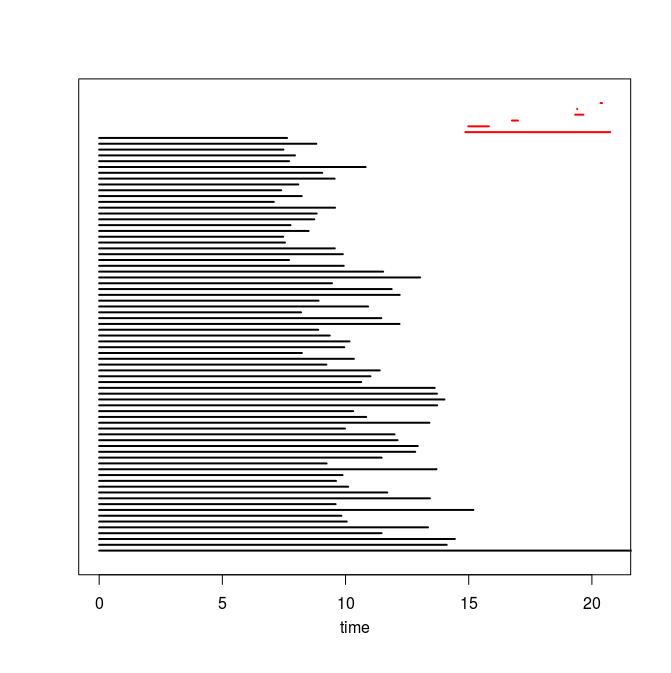
Q4. Use the code you implemented during the previous TD to compute the barcodes of the Rips filtrations. Here is our C++ code in case you do not have access to yours or yours is incorrect or inefficient. The resulting barcodes are shown below, arranged in the same way as the images above (click on a barcode to see it at full resolution). To visualize your own barcodes you can use the following R code, which allows you to write e.g. plot.barcode(diagram, maxdim=1) to plot the barcode (more precisely the intervals corresponding to homological features of dimension up to 1) stored in variable diagram, or alternatively, you can use the following Python code.
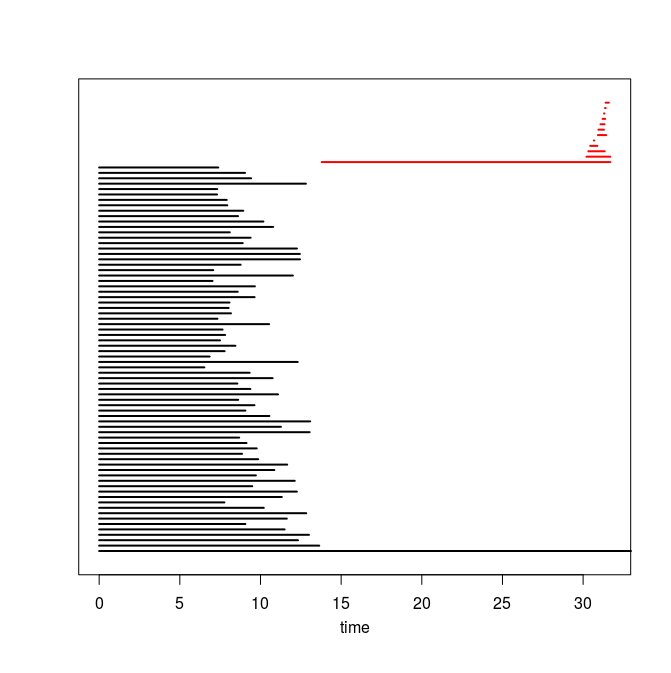
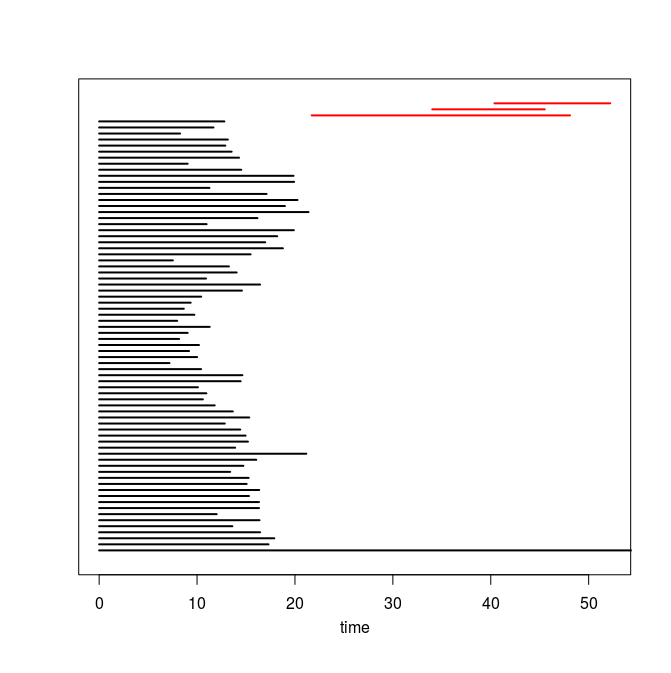
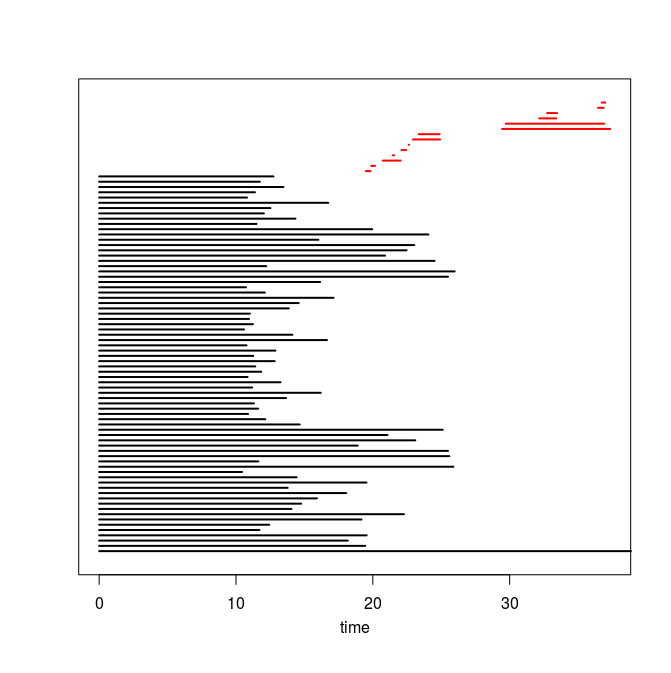
|
|
|
|
Q5. Compare each barcode against the corresponding 3d plot from question Q1. How did the projection down to R^3 influence the loops in the clouds? Compare your findings against the input images and clarify your interpretation of the presence of loops in terms of the properties of the acquisition process and of the symmetries in the objects.