TD 4 - Mean-Shift clustering et segmentation d'images

(application des Kd-trees)


Votre opinion sur le cours :

Introduction:

Dans ce TD nous allons implanter et tester un certain nombre de méthodes faisant intervenir des algorithmes de recherche géométrique (en dimension générique k). Pour faciliter votre travail, un certain nombres de primitives pour la manipulation de points en dimension kD (k arbitraire), ainsi que des classes pour la manipulation d'images en Java, seront fournies au cours de ce TD.

Fichiers et documentation pour le TD d'aujourd'hui:

Mean-shift clustering: une petite introduction

Dans ce TD nous considérons un algorithme de clustering connu sous le nom de Mean-Shift:  en particulier, nous verrons une application au problème de la segmentation d'images.

Segmentation d'images

La classe ImageManipulation met à disposition un certain nombre de méthodes pour manipuler des images en différentes formats, comme:

Segmentation d'images et clustering

Segmentation L'idée de base est très simple: on part d'une image de dimension NxM pixels, et on envoie chaque pixel sur un point dans un espace de couleurs de dimension 3 (ici espace Luv). On obtient ainsi un nuage de N.M points dans R^3. On applique un algorithme de clustering (Mean-Shift aujourd'hui) sur ce nuage afin de determiner une classification des points (et donc des pixels de l'image). Une fois les clusters calculés, on associe à tous les points (pixels) d'un meme cluster la meme couleur: cette phase est déjà codée et mise en place par la classe ImageSegmentation.

Clustering (Idée générale: plus de détails dans la suite) On traite l'ensemble des points comme provenant d'une fonction de densité de probabilité (qu'on ne connait pas explicitement, bien sur): les régions de l'espace où la densité est forte correspondent aux maximaux locaux (modes) de la distribution sous-jacente. L'algorithme de clusterting appelé Mean-Shift consiste à effectuer des estimations locales du gradient de la densité aux points de données, puis à bouger ces points le long du gradient estimé de manière itérative, jusqu'à ce qu'il y ait convergence: les points stationnaires de ce procedé correspondent aux maximaux locaux de la distribution. Et finalement, les points qu'on associe à un meme point stationnaire seront classifiés comme faisant partie du meme cluster.

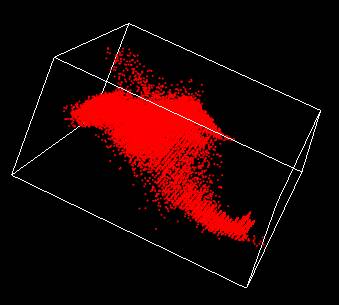
Voici un exemple:


Image originale (260x195 pixels)
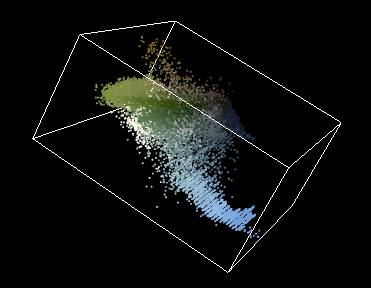
 Points dans l'espace Luv (3 dimensions)
 Après calcul des clusters avec Mean-Shift (le paramètre de bandwidth est fixé a 2.2, voir la section 2) Après segmentation





0. Pour commencer, quelques tests


Ouverture et affichage d'une image

On va commencer par effectuer des tests à l'aide de la classe TestIO. Pour executer le programme il faut lui passer en argument le nom d'un fichier image (.jpg, .bmp, .png) ou bien un fichier au contenant des nuages de points (.dat).

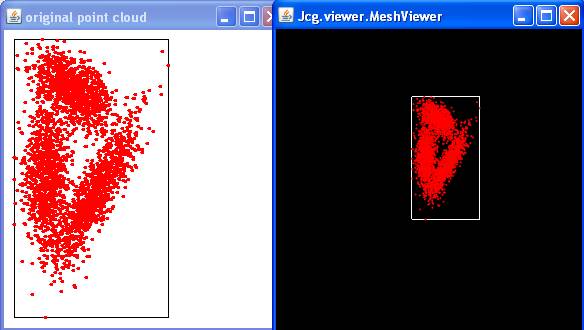
Voici les resultats qu'on peut obtenir.

  

java TestIO data/EP.jpg

 
java TestIO data/2D_dataset1.dat


Comment résoudre cet TD: en suivant des consignes... ou en partant de rien (selon vos gouts)


éléments dont vous disposez au cours de ce TD (un petit résumé)


Structures de données fournies
 RangeSearch, FastRangeSearch, SlowRangeSearch Implémentations éfficaces et naives de Range Queries


PointCloud
 Nuage de points: implementation à base de listes chainées

CoordinateComparator
 Un comparateur permettant de comparer les valeurs de la i-ième coordonnée de deux points
(utile pour trier un tableau (exo 1.1b), avec la méthode: Arrays.sort() )
Manipulation d'images et données
 Draw
 Méthodes pour la visualization de nuages de points en 2D et 3D

ImageManipulation (pour tester exo 0)
 Ouverture de fichiers images, calcul d'un nuage de points à partir d'une image (et viceversa)

Clustering
 Permet de manipuler des nuages de points et des clusters (ouverture de fichiers, ...)




Fichiers à compléter
 KdTree (exo 1)
 Implementation d'un Kd-Tree et du calcul des plus proches voisins


MeanShiftClustering (exo 2) Implementation de l'algorithme Mean-Shift

LinearTimeMedian (facultatif)
 implémentation de l'algorithme linéaire pour le calcule de la médiane




Fichiers de test
 TestIO (test exo 0) tests préliminaires sur les données en entrées

TestMedian (exo 1)
 Test pour le calcul de la médiane

TestKdTree (exo 1)
 Test sur la construction du Kd-Tree

TestRangeSearch Test la recherche des points proche avec Kd-tree (range search)

TestMeanShift (test exo 2)
 Test l' algorithme Mean Shift

TestImageSegmentation (test exo2) Permet d'appliquer le clustering à la segmentation d'images



Des squelettes à compléter (avec tests)

En partant de rien (ou presque)
Comme autrefois, on vous suggère de compléter les squelettes des fonctions (code déjà fourni). Dans ce cas, pour chaque exercice il vous reste à compléter le squelette d'une fonction, ainsi qu'à tester votre code avec des méthodes déjà fournies.
Et plus précisément, on vous demande de résoudre les questions dans cet ordre:




Exo 1: fichier KdTree.java
  • 1.1: calcul du point median d'un nuage de point (class LinearTimeMedian() )
  • 1.2: construction récursive d'un Kd-Tree, pour un nuage de points donné (constructor KdTree(PointCloud N, int pDim, int cutDim) )
  • 1.3: calcul des voisins d'un point donné: les points se trouvant à distance au plus R d'un point donné (fonction OrthogonalRangeSearch(Point_D q, double sqRad) )



Exo 2: fichier MeanShiftClustering.java
  • 2.1: détection d'un cluster
  • 2.2: fusion d'un cluster donné avec les autres déjà existants (se trouvant proche de ce cluster)
  • 2.3: détection de tous les clusters














Exo 3: fichier TestImageSegmentation.java
  • 3.1: application de Mean-Shift à la segmentation d'images (pas de code à écrire): effectuer des tests
  • 3.2: implementation d'une petite optimization pour le calcul du clustering (fichier MeanShiftClustering.java)
Dans ce cas on vous laisse plus de liberté dans la conception des structures de données et algorithmes: c'est à vous de choisir et mettre en place les structures que vous trouverez plus convenables pour une resolution éfficace des problèmes posés.
Bien sur, dans ce cas les méthodes fournies pour effectuer les tests ne sont pas censées fonctionner correctement: il vous faudra peut-etre les adapter.
On vous demande d'écrire deux classes comme suit:


Exo 1: Fournir la classe  KdTree des méthodes
  • public static KdTree constructDataStructure(PointCloud N, int pDim)
qui construit et renvoie un KdTree, correspondant à un nuage de point donné, en dimension pDim.
  • public PointCloud NearestNeighbor (Point_D q, double sqRad)
qui calcule et renvoie la liste des points qui sont à distance au plus squRad du point q (point de requete).



Exo 2: fournir la classe MeanShiftClustering de
  •  des données et paramètres suivants
    • N: nuage de points (input)
    • sqCvgRad: rayon de convergence (au carré)
    • sqAvgRad: rayon de la Fenetre (au carré)
    • sqInflRad: rayon d'influence (au carré)
    • sqMergeRad: distance de fusion (au carré)

  • public MeanShiftClustering (PointCloud n, double bandWidth)
le constructeur qui initialise la classe MeanShiftClustering (déjà fourni dans le squelette).

  • public Point_D[] detectClusters ()
qui met en place l'algorithme de clustering appelé Mean-Shift:




Exo 3: fichier TestImageSegmentation.java
  • 3.1: application de Mean-Shift à la segmentation d'images (pas de code à écrire): effectuer des tests
  • 3.2: implementation d'une petite optimization pour le calcul du clustering (fichier MeanShiftClustering.java)





1. Creation et manipulation des Kd-trees

Dans cet exercice on vous demande de compléter la classe KdTree: comme vu en cours aujourd'hui, les kD-trees permettent de répondre efficacement à des requetes de proximité géométrique, telles que le calcul des plus proches voisins (Nearest Neighbor Search) ou les "range search queries".

L'idée à la base de cet approche est très simple: on construit une décomposition récursive de l'éspace comme dans l'exemple ci-dessous.

Construction:

La construction de l'arbre (binaire) se réalise en effectuant un partitionnement récursif d'un nuage de points N à l'aide d'hyperplans séparateurs.
Les kD-trees sont des arbres binaires définis comme suit:
  • tout noeud est associé à un hyper-rectangle et contient les informations suivantes:
    • le nuage de points contenu dans l'hyper-rectangle (défini par la classe PointCloud)
    • les informations concernant le plan de coupe: la direction, ainsi que sa position (par construction le plan séparateur passe par la médiane)
  • les feuilles contiennent des points isolés (des PointCloud de taille 1)
  • la racine est le nuage de points initial N.
  • pour tout noeud de l'arbre, ses descendants sont les deux sous-graphes obtenus avec découpage à l'aide d'un plan séparateur (qui est, par construction, parallèle aux axes des coordonnées).
Recherche des plus proches voisins d'un points donné (à distance au plus R):

Le calcul des voisins d'un point donné q (plus proches d'une distance donnée), s'effectue récursivement à l'aide d'une visite de l'arbre (en partant de la racine).
A chaque étape il faut tester si le disque centré en q, et de rayon R, intersèctent ou pas le plan séparateur:
  • si le disque intersècte le plan séparateur, alors il faut continuer la recherche récursivement dans les deux sous-arbres (gauche et droit): le résultat de la requete sera alors l'union des deux requetes récursives dans les deux sous-arbres
  • s'il n'y a pas d'intersection avec le disque séparateur, alors cela signifie que la recherche ne sera effectué que dans un seul sous-arbre (celui dont le rectangle correspondant contient le point q): dans ce cas, il faut determiner si le disque se trouve à "droite" ou à "gauche" du plan séparateur.


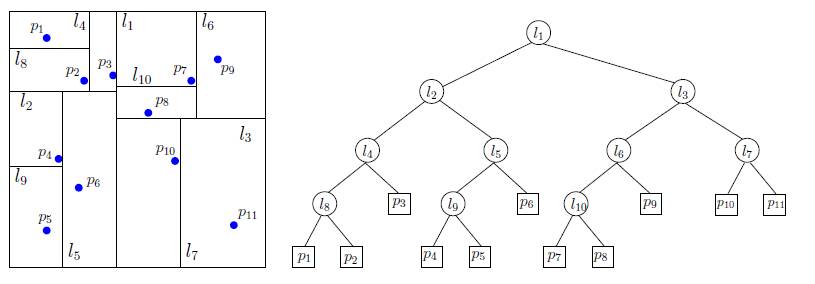
(exemple de 2d-Tree)

1.1 Calculer l'hyperplan séparateur

Le choix de l'hyperplan separateur (parallèle aux axes) peut se faire de plusieurs manières différentes.
La direction du plan séparateur sera dénoté par une valeur cutDim, dans la suite: en dimension d, cutDim vaut  0 ... d-1.
Dans ce TD, on vous propose 3 méthodes: de préférence, on vous demande d'utilise celle basée sur le calcul de la mediane avec un algorithme de complexité linéaire.

Les images ci-dessous illustrent les trois méthodes possibles.







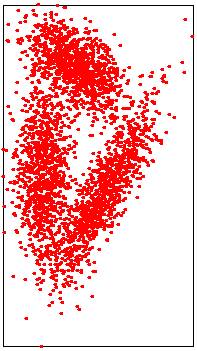
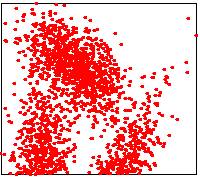
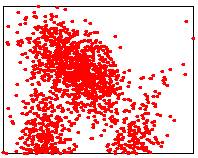
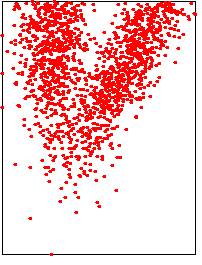
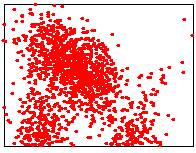
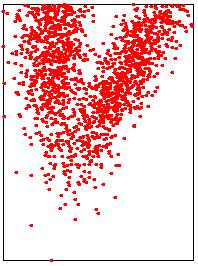
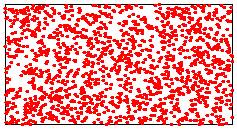
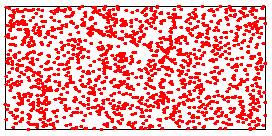
Input point cloud
 Mediane en temps linéaire
 Mediane de points triés (nlog n)
 Avec barycentre (temps linéaire)
 Médiane linéaire: points aléatoires

Lower points: 1214/3000 Lower points: 1500/3000 Lower points: 1596/3000
 Lower points: 1489/3000


1.1a Calculer la médiane en temps linéaire (facultatif)

 voici quelque résultats
Pour le calcul de la médiane on vous suggère de mettre en place l'algorithme de complexité linéaire vu en cours aujourd'hui seulement s'il vous reste de temps à la fin du TD.

Vous avez à compléter les deux fonctions suivantes:
  • private static Point_D findMedianArray (Point_D[] buffer, int max, int cutDim)
qui renvoie la médiane d'un tableau de taille max, pour des tableaux de petite taille (max sera au plus 5, dans la pratique). Le paramètre cutDim indique la direction de la coupe.

  • private static Point_D findMedianLinear (PointCloud N, int cutDim)
qui renvoie la médiane des cutDim-èmes coordonnées du nuage de points N. La mediane est calculée avec l'algorithme de complexité linéaire vu en cours: on décompose le nuage de points en tableaux de taille 5, pour lesquels on peut appeler la fonction précédente. Ensuite on appelle récursivement la fonction findMedianLinear pour calculer la médiane du nuage de points constitué des medianes des points stockés dans les tableaux.





1.1b Calcul de la médiane de points déjà triés

 voici quelque résultats
Pour le calcul de la médiane on peut d'abord trier le nuage des points (par rapport à la direction de coupe).
On vous demande de compléter la fonction suivante:
  • private Point_d findMedian (PointCloud N, int cutDim)
qui renvoie la médiane d'un nuage de points (après avoir trié les points selon la direction de coupe).

Suggestion: on pourra se servir de la fonction auxiliaire

  • private Point_d selectWithSorting (Point_D[] buffer, int index, int cutDim)
qui renvoie le i-ième élément d'un tableau qu'il faut trier: on pourra se servir de la méthode Arrays.sort() , qui permet de trier un tableau d'objets, muni d'un comparateur (voir classe CoordinateComparator).





1.1c Utiliser le barycentre
Pour le calcul du plan séparateur vous pouvez aussi vous servir du barycentre de l'ensemble de points: dans ce cas vous n'avez rien à coder pour l'instant... passez à l'exo suivant.

Rappel: le barycentre d'un nuage de points est déjà codé par la méthode PointCloud.mean(PointCloud N).



1.2 Construction d'un Kd-Tree

Il vous reste maintenant à compléter le constructeur de la classe KdTree, qui construit de manière récursive un arbre correspondant à un nuage de points donné.
Complétez le constructeur
Input:

Idée pour la solution: vous pouvez vous inspirer des étapes suivantes:
Entrees: N, pDim, cutDim

Initialiser les données associées à un noeud donné du KdTree
 - pDim, cutDim, points, numPoints

Calculer la valeur de coupe (cutValue)
 - avec la mediane
 - ou bien avec le barycentre

A partir du nuage N, 
 - creez deux sous listes lowerN et upperN: elles partitionnent la liste N 
   et correspondent aux points plus petits (ou plus grands) de la valeur cutValue
   (selon la direction définie par cutDim)

Testez si jamais les deux sous-listes ne contiennent pas de points

 - si jamais les sous-listes ne sont pas vides
     alors créer des sous-arbres de manière récursive
      (en passant les bons arguments, notamment la direction de coupe, qui devrait changer)

 - si jamais les deux sous-listes sont vides (les deux)
     retourner null (on est dans une feuille du Kd-Tree)


Pour tester, vous pouvez faire appel à la class TestKdTree.
Voici le résultat: (lecture du nuage de points dans 2D_dataset1.dat)

Exercice 1: testing Kd-trees
reading point cloud from file TD/input/dataset1.dat ... done
Drawing point cloud in 2D... 
Warning: drawing in dimension 3 a cloud of points of dimension 2
visualizing 3D point cloud
exercice 1.2: constructing Kd-Tree

size original point cloud: 3000
size Kd-Tree (total number of nodes): 5999
number of leaves in the tree: 3000
Bad balance in kd-tree! (521/634=0.8217665615141956)
end

1.3 Range Search

Il vous reste maintenant à compléter la méthode suivante, qui calcule manière récursive les points à distance au plus sqRad d'un point donné.
Input:

Vous pouvez vous inspirer des étapes suivantes
OrthogonalRangeSearch(Nuage n, point q, distance R)

si on a atteint une feuille de l'arbre
	retourner le point s'il est à distance R du point q (ou les points, si plusieurs)

sinon
	
  tester si le disque intersecte ou pas le plan séparateur

     - si le plan séparateur n'intersècte pas le disque (alors un seul des deux sous-noeud est à traverser)

        trouver le sous-noeud S de l'arbre dont le rectangle correspondant touche le disque
	appeler récursivement la fonction NN() sur le noeud S
 
     - sinon (les deux sous-noeud sont à traverser)

	appeler récursivement NN() sur les deux sous-arbres S1 et S2
	soit L1=NN(S1)
	soit L2=NN(S2)

	retouner L1 union L2


Pour tester, vous pouvez faire appel à la classe  TestRangeSearch

Voici le résultat avec  java RangeSearch


 
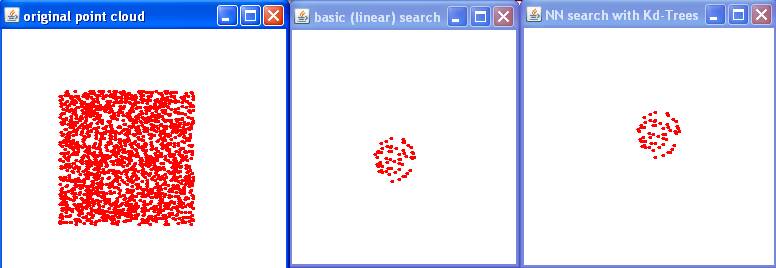
Exo 1.3: testing Range Search
Generated point cloud from random points in dimension 3
Drawing point cloud in 2D... 
warning: wrong point dimension 3
visualizing 3D point cloud
Computing Kd-Tree data structure...  done
visualizing 3D point cloud
basic search: 1165 neighbors
visualizing 3D point cloud
Kd-Trees search: 1165 neighbors
Range Search performaces:
Total construction time: 0s 32ms
Total NN query time: 0s 0ms

Testing Range Search: end
                 nuage orginal          ---            voisins calculés avec recherche linéaire        ---       voisins calculés avec Kd-Trees

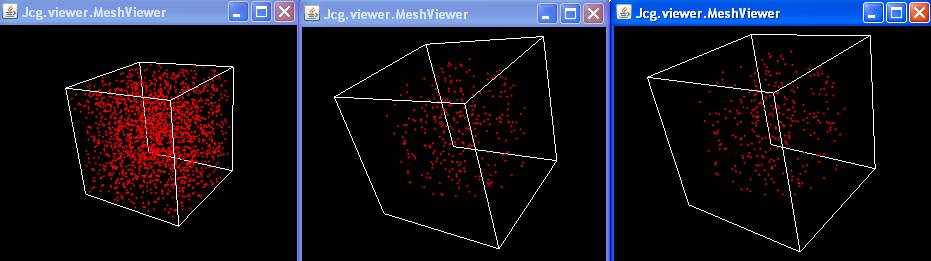
Exemple de range search en 3D

Nuage input: points aléatoires distribués uniformement dans le carré unité

Output: voisins se trouvant dans une boule


Remarque: les 3 images ne sont pas affichées à la meme échelle


Voici le résultat avec  java RangeSearch dataset1.dat
Exo 1.3: testing Range Search
reading point cloud from file TD/input/dataset1.dat ... done
Drawing point cloud in 2D... 

basic search: 43 neighbors
Warning: drawing in dimension 3 a cloud of points of dimension 2
visualizing 3D point cloud
Kd-Trees search: 43 neighbors
Range Search performaces:
Total construction time: 0s 31ms
Total NN query time: 0s 0ms

Testing Range Search: end

2. implementation de l'algorithme de clustering

Dans cet exercice on vous demande de compléter la classe MeanShiftClustering: comme vu en cours aujourd'hui, l'algorithme Mean-Shift consiste à classifier tous les points en entrés.

Remarque: pour plus de détails vous pouvez consulter les transparents (page web du cours)

Remarque (importante): comment représenter la partition en clusters

La classe Cluster permet de décrire comment les points sont associés aux clusters (une fois calculés). Pour se faire, on utilise une table de hachage:
qui permet d'associer un entier (Integer) à chaque point en entrée (de type X): il s'agit de l'indice i du cluster contenant le point, lorsque le calcul a été effectué (i prend des valeurs entre 0... C-1, où C est le nombre de clusters)

La classe MeanShiftClustering contient
qui permet d'initialiser toutes les valeurs ci-dessus, en fonction du paramètre bandwidth (donné en input à l'algorithme).

Pour ce qui est du TD d'aujourd'hui, on suggère d'utiliser comme bandwidth des valeurs réelles entre: 0.5 et 4.0

2.1 Detection d'un cluster

Il vous reste maintenant à compléter la méthode suivante, qui calcule un cluster à partir d'un point donné seed.
Input:
Output

Pour tester, vous pouvez faire appel à la classe  TestMeanShift (fonction  testDetectCluster(N, bandWidth)  dans le main)
Voici le résultat avec  java MeanShiftAlgorithm dataset1.dat 0.9

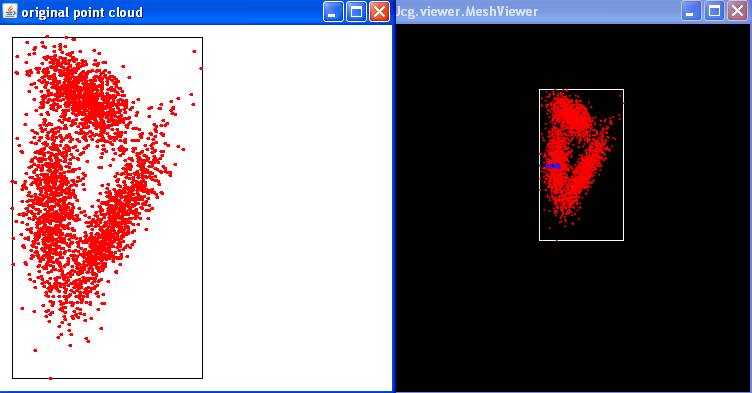
Exercice 2:
reading point cloud from file data/input/2D_dataset1.dat ... done
point cloud of size: 3000
Drawing point cloud in 2D...
Exercice 2.1: testing detecting a cluster

size of the detected cluster: 53
size of the cluster: 52
Warning: drawing in dimension 3 a cloud of points of dimension 2
visualizing 3D point cloud
Range Search performaces:
Total construction time: 0s 31ms
Total NN query time: 0s 0ms

Total time to find clusters: 0s 265ms

Sortie à la console


Voici le résultat avec  java TestMeanShift 0.9

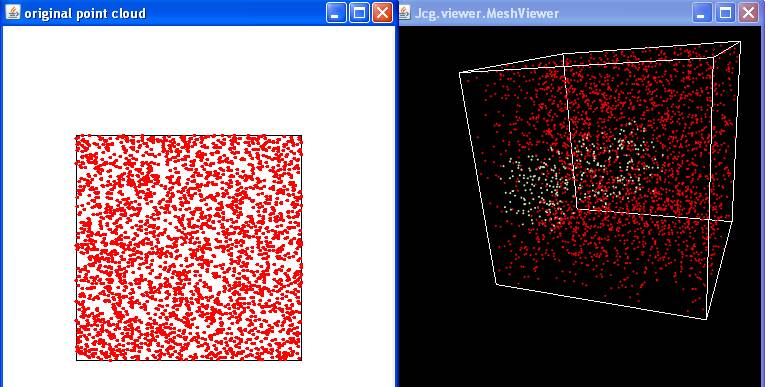
Exercice 2:
Generated point cloud from random points in dimension 3
point cloud of size: 3000
Drawing point cloud in 2D...
warning: wrong point dimension 3
Exercice 2.1: testing detecting a cluster
size of the detected cluster: 315
size of the cluster: 314
visualizing 3D point cloud
Range Search performaces:
Total construction time: 0s 31ms
Total NN query time: 0s 0ms

Total time to find clusters: 0s 281ms

Sortie à la console


2.2 Fusion de clusters

Dans cet exercice vous devez réaliser la fusion d'un cluster donné avec un autre parmi ceux qui sont déjà existants: un cluster C1 est fusionné avec un cluster Ci si les deux maximaux sont à distance au plus R.

Complétez la fonction
Input:
Output

Pas de test pour cette fonction


3.3 Calcul de tous les clusters

Maintenant vous disposez de tous les outils pour détecter, de manière itérative, tous les clusters.
Complétez la fonction
qui implémente l'algorithme Mean-Shift, en classifiant tous les points du nuage original N (stoqué dans la classe MeanShiftClustering )

Output

Suggestion: vous pouvez vous inspirer des étapes suivantes
// initialiser la structure de donnees
- creer un tableau clusterCenters de type Point_D, de taille |N| (au debut les cases sont toutes null)
	//(ce tableau contient les points stationnaires des clusters detectés, jusqu'à une certaine étape)
- initialiser une variable NbClusters=0, pour compter le nombre de clusters detectés


// procedure iterative de detection des clusters

Tant qu'il existe des points non classifiés

   - choisir un point P (centre d'une Fenetre)
   si jamais P est déjà classifié, on ne fait rien

   sinon
	- calculer le cluster associé à P    // avec la fonction detectCluster()	
	soit la liste L(P) des points classifiés dans le cluster de P 

   - tester si L(P) peut etre fusionnée avec d'autres clusters déjà existants
	(pour cela il on peut utilisé le vecteur clusterCenters)

   - si on ne peut pas fusionner le cluster alors
	ajouter ce cluster aux existants
	   // (ajouter le point stationnaire correspondant au tableu clusterCenters)

retourner comme sortie le tableau clusterCenters


Pour tester, vous pouvez faire appel à la classe  TestMeanShift (fonction testMeanShift(N, bandWidth)  dans le main)
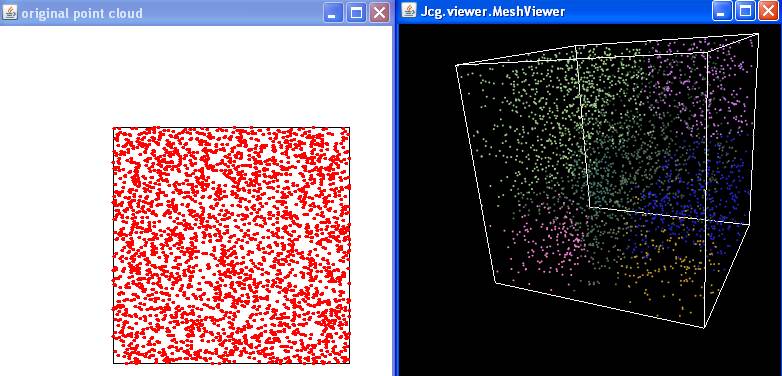
Voici le résultat avec  java MeanShiftAlgorithm  0.3
        Exercice 2:
Generated point cloud from random points in dimension 3
point cloud of size: 3000
Drawing point cloud in 2D...
warning: wrong point dimension 3
Exercice 2.3: testing Mean-Shift clustering
Initializing data structure... done

Number of clusters detected: 9
visualizing 3D point cloud
Range Search performaces:
Total construction time: 0s 32ms
Total NN query time: 2s 609ms

Total time to find clusters: 3s 750ms
nuage avant  et après clustering Sortie à la console


Voici le résultat avec  java MeanShiftAlgorithm dataset3.dat 1.2
  
Exercice 2.3: testing Mean-Shift clustering

Initializing data structure... done

Number of clusters detected: 3
Warning: drawing in dimension 3 a cloud of points of dimension 2
visualizing 3D point cloud
Range Search performaces:
Total construction time: 0s 563ms
Total NN query time: 13s 791ms

Total time to find clusters: 23s 47ms
dataset3.dat
 Sortie à la console


3. clustering et segmentation d'images

Dans cet exercice on vous demande de tester avec la classe TestImageSegmentation.

Remarque: vous n'avez plus rien à coder (ou presque): une fois l'algorithme de clustering bien implementé, la segmentation d'image est effectuée par la classe TestImageSegmentation, dont les méthodes fournissent tout le nécéssaire pour obtenir, à partir d'un nuage de points partitionné en clusters, l'image segmentée correspondante.

3.1 Tester l'algo de segmentation d'images (pas de code à écrire)

Il ne vous reste qu'à faire des expéreinces sur les images de test, à l'aide de la fonction main de la classe ImageSegmentation.

Afin de se rendre compte de l'utilité des Kd-Trees, vous pouvez chercher à effectuer deux types de tests,
Pour cela il suffit de changer le choix de l'impl'ementation de l'interface RangeSearch.


Voici nos images après segmentation, obtenues en executant par exemple:
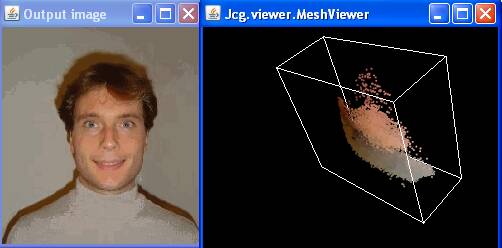
java TestImageSegmentation Steve.jpg 2.0
Bandwidth 2.0, 51957 pixels, 608 detected clusters Bandwidth 2.0, 53280 pixels, 161 detected clusters
efficient NN search (with Kd-Trees)
 Total time to find clusters: 21s 781ms

Range Search performaces:
Total construction time: 0s 953ms
Total NN query time: 15s 725ms
 efficient NN search (with Kd-Trees)
Total time to find clusters: 20s 437ms

Range Search performaces:
Total construction time: 0s 985ms
Total NN query time: 14s 405ms

basic NN search (linear time search)
 Total time to find clusters: 597s 375ms

Range Search performaces:
Total NN query time: 588s 893ms
basic NN search (linear time search)
Total time to find clusters: 311s 781ms

Range Search performaces:
Total NN query time: 304s 236ms


3.2 Apporter une petite amélioration

On va mettre en place une dernière petite optimisation, afin de réduire le temps de calcul (et le nombre de cluster): comme on peut le voir sur la sortie, le gain en termes de temps de calcul est non negligeable, alors que le résultat final (la qualité de la segmentation) est très proche de ce qu'on obtient sans optimisation.

L'idée de base est très simple: à la fin de la procedure pour detecter un clustering, après avoir atteint la convergence, on ajoute au clustering tous les points qui se trouvent dans la fenetre (le disque)  dont le centre est le point stationnaire qu'on vient de determiner.
Cela a pour effet d'augmenter "legerement" le nombre de points qui appartiennent au cluster calculé: ce qui reduit le nombre de points à classifier dans les étapes successives.

Modifiez la fonction
afin de mettre en place cette amélioration.

Voici quelque résultat
EP, 50700 pixels, bandwidth 2.5,

Detected clusters 1113...
without optimization

Total time to find clusters: 52s 406ms

Range Search performaces:
Total construction time: 1s 0ms
Total NN query time: 35s 715ms
 EP, 50700 pixels, bandwidth 2.5,


with optimization

Total time to find clusters: 43s 469ms

Range Search performaces:
Total construction time: 1s 31ms
Total NN query time: 28s 758ms