TD 6 - machine virtuelle à pile

Nous nous proposons dans ce TD de développer un interpréteur pour une machine à pile. Pour ce TD, nous vous fournissons une bibliothèque un parseur pour le langage assembleur de la machine virtuelle et nous concentrerons sur l’écriture de l’interpréteur.

Par la suite, lors d’une future session, nous écrirons un compilateur pour un langage While qui génèrera du code pour ladite machine virtuelle.

La machine virtuelle

La machine virtuelle que nous allons implémenter à les caractéristiques suivantes:

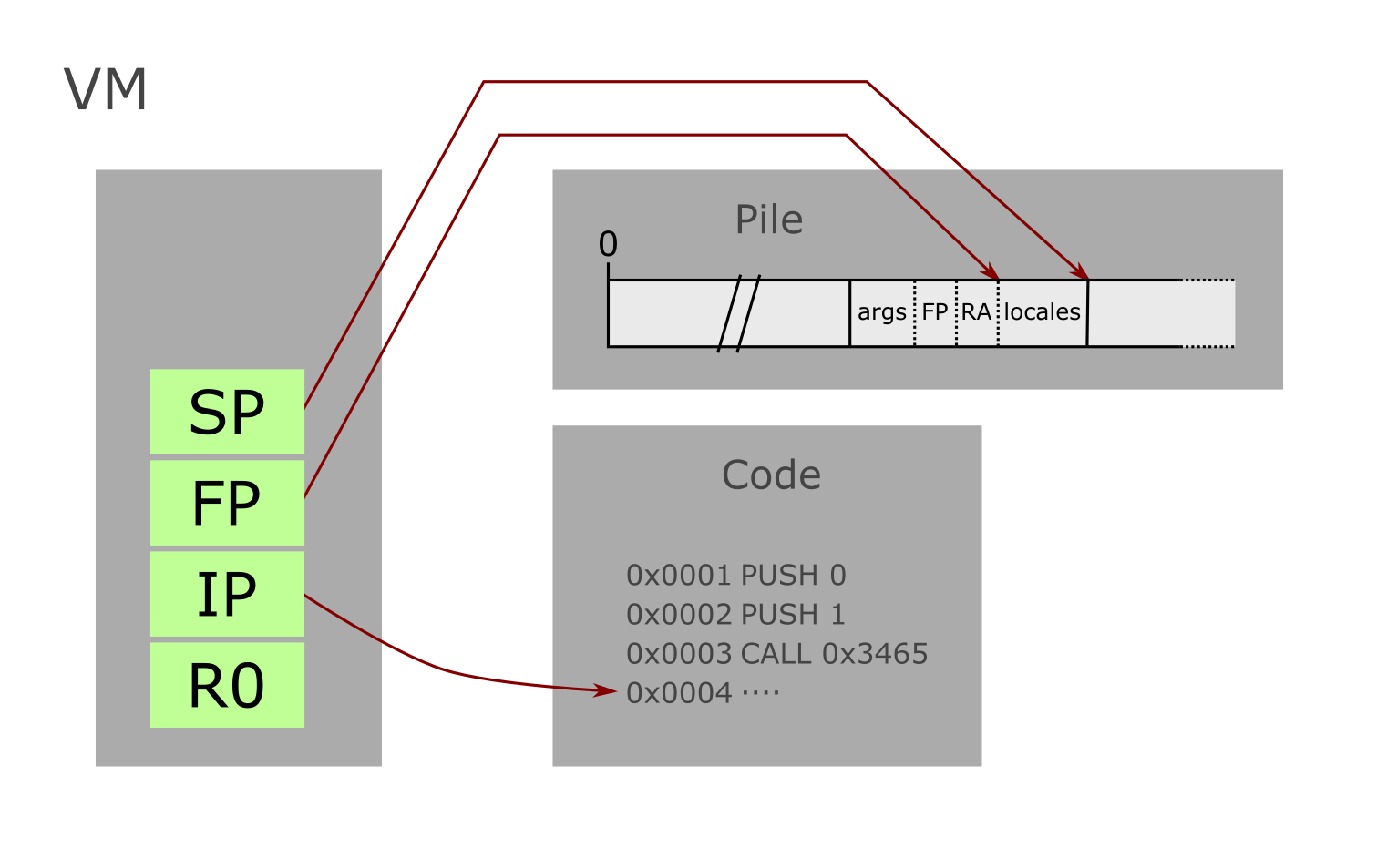
• la machine ne sait que manipuler des mots machine (ici, des entiers 64-bits signés - cf. le module Int64 de OCaml).
• la machine possède une unité arithmétique et logique pour la calcul de la plupart des opérations arithmétiques et logiques.
• la machine a accès à une pile sur laquelle il est possible de pousser ou extraire des mots machines. Les cellules de la pile sont numérotées à partir de 0.
• la machine possède 3 registres dédiés ainsi qu’un registre général. Les 3 registres dédiés sont le pointeur de pile (stack pointer ou SP), le pointeur de frame (frame pointer ou FP) et le pointeur d’instruction (instruction pointer ou IP). Les deux premiers registres SP et FP serviront à la construction de l’activation frame des procédures (qui sert à stocker les arguments, l’adresse de retour et les variables locales d’une procédure), alors que IP sert à mémoriser la future instruction à exécuter. Enfin, on nomme R0 le registre général. Tous les registres peuvent stocker exactement un mot.
• la machine possède un espace mémoire où est stocké le code à exécuter. Ce dernier est stocké sous forme logique - une instruction occupe exactement une case mémoire. Les cases mémoires sont numérotées à partir de 0 et le code est toujours chargé à l’adresse 0.

Op-codes

On donne dans cette section les types d’adressage possibles, ainsi que la liste des op-codes et la liste des instructions arithmetico-logiques.

Constantes machines

Certaines opérations peuvent manipuler des valeurs constantes directement.

On utilise la méta-variable $imm pour les constantes machines.

Adresse de pile

On rappelle que la pile de la machine est constitutée de cellules pouvant contenir chacun un mot et dont la première est à l’index 0. Il n’est pas possible de référencer une cellule directement par son index absolu mais relativement, via un offset, au registre SP ou FP. La syntaxe d’une telle adresse est %r+$imm (resp. %r-$imm) où r est SP ou FP et $imm est une constante. Une telle adresse référence la cellule dont l’index est égal au contenu du registre r auquel on a rajouté (resp. retranché) $imm.

Par convention, on appelle tête de pile la cellule dont l’index est %SP-1.

On utilise la méta-variable $address pour les adresses de pile.

Adresse d’instruction

La machine virtuelle possède un espace dédié au stockage du code à exécuter. Nous rappelons que ce dernier est stocké sous forme logique - une instruction occupe exactement une case mémoire. Les cases mémoires sont numérotées à partir de 0 et le code est toujours chargé à l’adresse 0.

Une adresse d’instruction est simplement une constante indique l’index de la case mémoire de l’instruction dans la mémoire dédiée.

On utilise la méta-variable $label pour les adresses d’instruction.

Liste des op-codes

La machine virtuelle possède 12 instructions, dont on donne le détail ci-dessous (Note: la résolution des adresses doit être faite avant le début de l’exécution de l’instruction. Par exemple, POP %SP-2 résoud %SP-2 avant de commencer à modifier la valeur de SP):

Les instructions RET et CALL seront utilisées pour l’appel de procédures. On donnera les détails de convention d’appel dans la seconde partie de ce projet. Pour le moment, vous avez seulement besoin de savoir que:

• CALL pousse le contenu de FP et IP sur la pile (dans cet ordre), affecte à FP le contenu de SP, puis saute à l’adresse $label.
• RET affecte à SP le contenu de FP, puis dépile (2x) le haut de pile dans IP puis FP (dans cet ordre).

Liste des opérations arithmetico-logiques

La machine virtuelle donne accès à un ensemble d’opération arithmetico-logique, dont on donne le détail ci dessous. Les instructions arithmétiques sont toutes signées. Les instructions logiques considère le mot constant 0 comme la valeur de vérité fausse, et toute autre constante comme la valeur de vérité vraie. Les arguments des opérations sont lus sur la pile (de gauche à droite du haut de la pile vers sa base) pour les opérateurs prenant plusieurs arguments.

Travail demandé

À la fin de cette partie, vous devrez déposer votre assembleur:

On vous demande d’implémenter un évaluateur pour la machine virtuelle présentée ci-dessus. Ainsi,

1. Définissez les structures de donnée nécessaires à la représentation des opcodes (incluant les constantes, les différents modes d’adressage et les codes de l’ALU).

   type word = Int64.t
   
   type alucode = ...
   type address = ...
   type opcode  = ...

   On rappelle que les mots machines sont de taille 64-bits. Le module OCaml Int64 (doc) contient un tel type. Il est possible de créer des valeurs litérales de type int64 via la syntaxe xxxL, par exemple 10L ou 0x1aL en hexadécimal.

2. Écrivez une structure de donnée pour représenter l’état de la machine, à savoir, l’état de ses registres et de sa pile. Structurez autant que possible votre code, c’est-à-dire faites un module dédié pour la gestion de la pile (VMStack) et un pour la gestion de l’ensemble des registres (VMRegister). Ces structures seront par la suite utilisée de manière impérative, on vous demande d’éviter de faire des structures fonctionnelles pour ce TD. Notamment, la pile sera de taille fixe, qui sera donnée à l’initialisation, et devra permettre les accès aléatoires en lecture/écriture. (Vous pouvez regarder la question suivante pour avoir une idée des fonctionnalités demandées)

   module VMStack : sig
       type stack
   end = struct
     ...
   end
   
   module VMRegister : sig
       (* Enumeration of the registers (by name) *)
       type register = SP | FP | IP | R0
   
       (* Holds the values for the 4 aforementioned registers *)
       (* A register can store exactly of word *)
       type registers
   end = struct
     ...
   end
   
   type vm = ...

3. Complétez les modules VMStack et VMRegister:

   type vmerror =
     | InvalidAddress
     | DivisionByZero
   
   exception VMError of vmerror
   
   module VMStack : sig
     type stack
   
     (* [create sz] create a new stack of capacity [sz] *)
     val create : int -> stack
   
     (* [capacity st] returns the capacity, in words, of [st]. *)
     val capacity : stack -> int64
   
     (* [get st idx] returns the word located at index [idx] in [st].
        Raise [VMError InvalidAddress] if [idx] is valid *)
     val get : stack -> int64 -> word
   
     (* [set st idx w] sets to [w] the word located at index [idx]
        Raise [VMError InvalidAddress] if [idx] is valid *)
     val set : stack -> int64 -> word -> unit
   end
   
   module VMRegister : sig
     type registers
     type register = SP | FP | IP | R0
   
     (* All registers should default to 0 *)
     val create : unit -> registers
   
        (* Register setter *)
        val set : registers -> register -> word -> unit
   
        (* Register getter *)
        val get : registers -> register -> word
   end

4. Implémentez un module ALU pour les instructions arithmetico-logiques. Le module Int64 vous fournira toutes les opérations nécessaires:

   module ALU : sig
     val op_add   : word -> word -> word
     val op_sub   : word -> word -> word
     val op_mul   : word -> word -> word
     val op_div   : word -> word -> word
     val op_neg   : word -> word
     val op_lt    : word -> word -> word
     val op_le    : word -> word -> word
     val op_land  : word -> word -> word
     val op_lor   : word -> word -> word
     val op_lnot  : word -> word
   end = struct
     let b2w (b : bool) = if b then 1L else 0L
   
     let op_add = Int64.add
     ...
   end

5. Écrivez les fonctions principales pour charger et évaluer les opcodes:

   exception VMStop
   
   (* Fetch and return the currently IP-pointed opcode in [vm].
      * This function also increments the IP register so that it
      * points to the next opcode. *)
   let fetch (vm : vm) : opcode = ...
   
   (* Execute on [vm] the opcode [oc]. Raise [VMStop] when of the [vm]
    * wants to halt. *)
   let exec1 (vm : vm) (oc : opcode) : unit = ...
   
   (* Continuously fetch/exec until the [vm] wants to halt *)
   let exec (vm : vm) : unit = ...

6. À ce stade, il ne vous reste plus qu’à permettre la création d’une machine virtuelle à partir d’un programme:

   val create : opcode array -> vm

   et de la tester sur le code suivant qui calcule la factorielle de 4 (en traduisant le programme à la main vers une liste d’opcode en OCaml):

   CALL   0x13
   STOP
   PUSH   0x01
   PUSH   %FP-3
   PUSH   0x00
   ALU    LT
   POP
   JMPZ   0x11
   PUSH   %FP-3
   PUSH   %FP+0
   ALU    MUL
   POP    %FP+0
   PUSH   0x01
   PUSH   %FP-3
   ALU    SUB
   POP    %FP-3
   JMP    0x03
   LOAD   %FP+0
   RET
   PUSH   0x04
   CALL   0x02
   DCD    0x01
   PRT
   RET

7. Il n’est pas toujours aisé de faire le calcul des adresses de code à la main pour les sauts, et surtout de le maintenir, l’ajout d’une instruction décalant toutes les adresses de 1. Pour palier ce problème, nous allons introduire des adresses logiques (ou étiquettes) qui seront ensuite résolues vers des adresses de code.

   1. Définir un type xopcode, similaire au type opcode ci-dessus, mais qui est paramétrique en le type des adresses de code. En redéfinissant opcode comme alias de type pour word xopcode, votre interpréteur devrait fonctionner sans modification.

      type 'lbl xopcode = ...
      
      type opcode  = word   xopcode
      type lopcode = string xopcode

      L’alias de type lopcode représente quant à lui un opcode où les adresses de code sont des étiquettes (string).

   2. Définissez un type srcasm dont les valeurs sont soit un lopcode (OPCode oc), soit une étiquette (Label lbl). Ce dernier permettra de marquer des endroits du code grâce à une étiquette et d’y faire référence par la suite dans les instruction JMP & JMPZ.

      type srcasm = ...

   3. Écrivez une fonction

      val resolve : srcasm list -> opcode list

      qui assemble un programme sous la forme d’une liste de srcasm en résolvant toutes les adresses logiques.

   4. Testez votre programme sur le code suivant (les entrées de la forme .label: indique où pointe, dans le code, l’étiquette label):

      .entry:
       CALL  main
       STOP
      .fact:
       PUSH  0x01
      .fact_loop:
       PUSH  %FP-3
       PUSH  0x00
       ALU   LT
       POP
       JMPZ  fact_end
       PUSH  %FP-3
       PUSH  %FP+0
       ALU   MUL
       POP   %FP+0
       PUSH  0x01
       PUSH  %FP-3
       ALU   SUB
       POP   %FP-3
       JMP   fact_loop
      .fact_end:
       LOAD  %FP+0
       RET
      .main:
       PUSH  0x04
       CALL  fact
       DCD   0x01
       PRT
      .main_end:
       RET