

TD 3 : Programmation Fonctionnelle
Déposer le fichier ho.ml :
Écrire une fonction qui calcule la somme \(\sum_{i=1}^n i\) (sans multiplication)
Écrire une fonction qui calcule la somme \(\sum_{i=1}^n i^2\).
À l’aide de l’ordre supérieur, écrire une fonction qui calcule la somme \(\sum_{i=1}^m f(i)\) où \(f\) est donnée en argument. En déduire une réimplémentation des deux questions précédentes.
Écrire une fonction d’ordre supérieur dicho t.q. dicho f (a, b) e retourne une paire (u, v) t.q. l’intervalle [u,v] est de longueur inférieure à e et contient un zéro de f (sous l’hypothèse que f est de type float -> float, continue, monotone, et \(f(a) \cdot f(b) < 0\).
Une structures de données persistantes est une structure de donnée qui, lors d’une modification, préserve les versions précedentes. Par exemple, les structures purement fonctionnelles sont immuables: on ne peut les modifier, mais seulement les copier, et sont donc automatiquement persistantes. Les listes ou les arbres tels que vous les avez vus dans les TD précédents sont des exemples de structures purement fonctionelles. On va s’intéresser ici à deux structures de données, les files et les tableaux, pour lesquelles nous allons écrire des versions persistantes.
Déposer le fichier queue.ml :
une file dite est une structure de données basée qui possède deux opérations push et pop, et qui repose sur le principe du premier entré, premier sorti (en anglais FIFO, first in, first out). Cela veut dire que les premiers éléments ajoutés à la file (via push) seront les premiers à en être retirés (via pull). On donne ci-dessous deux implémentations pour les files, une purement fonctionnelle (et donc persistante), et une impérative (en utilisant une liste mutable qui maintient une référence sur le premier et le dernier élément de la liste). Comprenez bien ce que font ces deux implémentations avant de continuer.
type 'a queue = 'a list
let empty : 'a queue =
[]
let is_empty (q : 'a queue) : bool =
match q with [] -> true | _ -> false
let push (x : 'a) (q : 'a queue) : 'a queue =
q @ [x]
let pull (q : 'a queue) : ('a * 'a queue) option =
match q with
| [] -> None
| x :: q -> Some (x, q)
type 'a cell = Void | Cons of 'a * 'a cell ref
type 'a queue = { mutable first : 'a cell;
mutable last : 'a cell; }
let create () : 'a queue =
{ first = Void; last = Void; }
let is_empty (q : 'a queue) : bool =
q.first = Void
let push (x : 'a) (q : 'a queue) : unit =
match q.last with
| Void ->
assert (q.first = Void);
q.first <- Cons (x, ref Void);
q.last <- q.first
| Cons (_, r) ->
r := Cons (x, ref Void);
q.last <- !r
let pull (q : 'a queue) : 'a option=
match f.first with
| Void ->
None
| Cons (x, r) ->
if f.last = f.first then f.last <- !r;
f.first <- !r; Some xL’implémentation impérative est ici clairement non-persistante. Cependant, sa complexité est bien meilleure: alors que l’ajout d’un élément dans la queue impérative se fait en temps constant, celui dans la structure purement fonctionnelle est en temps linéaire en le nombre d’éléments déjà présents dans la file. (Elle utilise une concaténation de liste à chaque insertion !)
Nous vous demandons maintenant d’implémenter une nouvelle version purement fonctionnelle des files qui aura une complexité amortie en temps constant. L’idée est la suivante: au lieu d’utiliser une liste pour stocker une file, deux seront utilisées. Ainsi, une paire de listes (s1, s2) représentera la file s2 @ List.rev s1. Pousser un élément dans la file se fera par une simple insertion de cet élément en tête de s1. De même, sortir un élément de la file se fait par simple retrait la tête de s2. Bien sûr, il se peut que s2 soit vide, et il faudra alors chercher l’élément à retirer dans s1.
Nous donnons ci-dessous les types des fonctions à implémenter:
type 'a queue = 'a list * 'a list
val empty : 'a queue
val is_empty : 'a queue -> bool
val push : 'a -> 'a queue -> 'a queue
val pull : 'a queue -> ('a * 'a queue) optionDéposer le fichier parray.ml :
Nous allons maintenant rendre persistente la structure de tableau ('a array). Votre implémentation reposera sur l’idée suivante (la solution consistant à copier le tableau à chaque modification est à proscrire !): un tableau persistent sera représenté soit directement par un tableau OCaml (type 'a array), soit par une indirection (i, v, a) représentant un tableau persistant en tout point identique à a, sauf à l’indice i où on trouve la valeur v.
Notez la présence de références qui nous permettra de changer la représentation, en place, du tableau persistant.
Il existe deux stratégies lors de la modification d’un élément du tableau, suivant que l’on décide de placer l’indirection sur le tableau en entrée ou sur le tableau en sortie, comme illustré ci-dessous:


Dans les deux cas, nous avons un tableau a égal à [|1; 2; 3|] dont nous modifions la 3ème cellule (d’indice 2) avec la valeur 7 – le résultat étant stocké dans la variable b. Dans le premier scénario, le tableau est modifié directement. Ainsi, b pointe vers le tableau [|1; 2; 7|] obtenu par mutation du tableau initial. Quant à la variable a, elle a été modifiée de manière à maintenant être une indirection: a est identique à b, sauf pour la cellule d’indice 2 qui est égale à l’entier 3. Dans le second scénario, c’est l’inverse. La variable a n’est pas modifiée et pointe toujours sur le tableau [|1; 2; 3|] qui est laissé intacte. En revanche, la variable b est définie comme une indirection: b est identique à a, sauf pour la cellule d’indice 2 qui est égale à l’entier 7.
Nous allons ici implémenter la première stratégie – l’hypothèse étant qu’il est plus probable qu’un accès à un tableau persistant se fasse sur les dernières versions du tableau plutôt que sur les premières. De plus, lors de la lecture d’un tableau, les indirections seront inversées – l’hypothèse étant ici que si on accède à un tableau, on risque d’y réaccéder par la suite et qu’il vaut mieux y supprimer les indirections qui peuvent être couteuses en temps d’accès. Ainsi, un accès au tableau a dans le premier scénario ci-dessus aménera à la représentation du deuxième scénario.
On vous demande:
d’implémenter une fonction norm : 'a parray -> unit qui normalise la tableau persistant donné en entré tel que ce dernier ne contienne plus d’indirections.
d’implémenter une fonction lift : ('a array -> 'b) -> 'a parray -> 'b qui relève une fonction pure (dans notre cas, qui ne modifie son argument) des tableaux OCaml vers les tableaux persistants.
d’implémenter les fonctions suivantes (dont on donne les types). Ces fonctions sont semblables à celle de la bibliothèque des tableaux de OCaml à une exception: la fonction set qui, au lieu de retourner la valeur (), retourne le tableau modifié. (Pour la documentation des fonctions, vous pouvez aller voir la documentation OCaml de la bibliotheque Array sur les tableaux.)
type 'a parray = ...
val create : int -> 'a -> 'a parray
val init : int -> (int -> 'a) -> 'a parray
val length : 'a parray -> int
val get : 'a parray -> int -> 'a
val set : 'a parray -> int -> 'a -> 'a parray
val tolist : 'a parray -> 'a list
val iter : ('a -> unit) -> 'a t -> unit
val iteri : (int -> 'a -> unit) -> 'a parray -> unit
val fold_left : ('a -> 'b -> 'a) -> 'a -> 'b parray -> 'a
val fold_right : ('a -> 'b -> 'b) -> 'a parray -> 'b -> 'bDéposer le fichier t9.ml :
Le mode T9 (text on 9 keys) était une méthode de saisie pour les téléphone portables à clavier numérique facilitant la saisie des textes. Les touches d’un clavier téléphonique étaient généralement disposées comme sur l’image ci-dessous : à chaque touche correspondait un groupe de plusieurs lettres (3 ou 4). Pour saisir une lettre, il fallait taper plusieurs fois sur une touche pour faire défiler les lettres correspondants à la touche.

Au lieu de cela, dans le mode T9, une seule frappe par lettre suffit et le téléphone propose de lui-même les mots, à partir d’un dictionnaire, qui correspondent à la séquence de touches qui vient d’être tapée.
Par exemple, la suite de touches 2, 6, 6, 5, 6, 8 et 7 correspond au mot bonjour. Cependant, il est possible qu’une suite de touches corresponde à plusieurs mots. Ainsi, la suite 8, 3, 6, 3, 7, 3 correspond aux mots tendre et vendre.
Le but de cette question est de programmer une solution pour la recherche des mots du dictionnaire qui correspondent à une séquence de touches. Pour cela, nous allons représenter le dictionnaire par un arbre de décision où chaque branche est étiquetée par le numéro d’une touche, et chaque noeud par les mots du dictionnaire correspondant à la séquence des touches menant de la racine à ce noeud. Nous donnons ci-dessous l’arbre de décision pour le dictionnaire bon, bonne, bonjour, vendre, tendre:
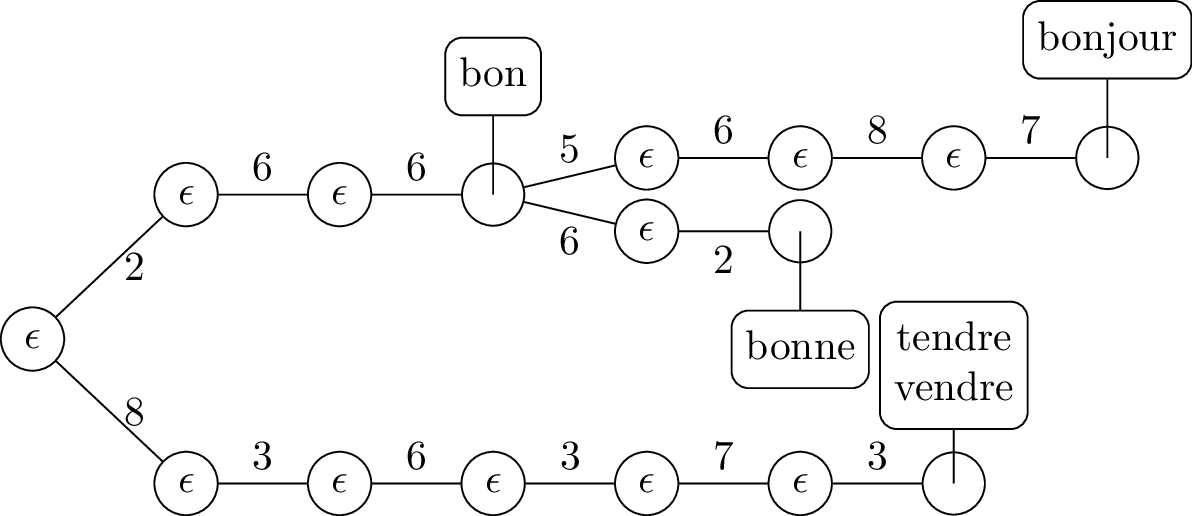
On vous demande:
de définir le type t9 pour l’arbre de décision tel que défini ci-dessus.
d’implémenter les fonctionnalités suivantes:
(* Dictionnaire T9 vide *)
val empty : t9
(* insert w d : ajoute le mot `w` au dictionnaire `d` *)
val insert : string -> t9 -> t9
(* remove w d : supprime le mot `w` du dictionnaire `d` *)
val remove : string -> t9 -> t9
(* search t d : retourne la liste de mots, à partir du
* dictionnaire `d`, correspond à la suite de touches `t` *)
val search : int list -> t9 -> string listPour tester votre implémentation, vous pourrez utiliser les fonctions suivantes:
let iofold (f : string -> 'b -> 'b) (fname : string) (x : 'b) =
let stream = open_in fname in
try
let rec aux (x : 'b) =
try aux (f (input_line stream) x)
with End_of_file -> x
in let x = aux x in close_in stream; x
with e -> close_in stream; raise eNous fournissons également un (petit) dictionnaire pour le français (non accentué).
Déposer le fichier future.ml :
L’évaluation paresseuse ou différée est une stratégie qui retarde l’évaluation d’une expression jusqu’à sa première utilisation. De plus, une fois calculée, le résultat de l’évaluation peut être préservé pour une réutilisation ultérieure. L’évaluation paresseuse peut être utilisée à des fins d’optimisation (une expression non utilisée ne sera pas évaluée et une expression sera évaluée au plus une fois), mais permet aussi de construire des types de données comme des listes infinies, que nous verrons à la question suivante.
Certains langages, comme Haskell, ont par défaut une stratégie d’évaluation paresseuse. OCaml, lui, a une stratégie d’évaluation stricte. Par exemple, tous les arguments d’une fonction sont évalués avant de procéder à l’appel.
On se propose dans ce TD d’écrire une implémentation de calculs différés pour OCaml. Concrètement, une évaluation différée sera représentée par une fonction de type unit -> 'a. Par exemple, définissons x comme suit:
Le corps des fonctions n’étant pas évalué tant que tous les arguments non pas été donnés, on obtient que x représente l’évaluation suspendue de l’expression 3 + 3. Il nous suffira d’appliquer x à () pour forcer cette évaluation. Cependant, à chaque fois que nous forcerons l’évaluation de x, le calcul de 3 + 3 sera fait – le résultat de la première évaluation n’est pas mémorisé.
Pour obtenir ce comportement, on peut se servir des références pour retenir l’évaluation de 3+3. Ainsi, nous pourrions modifier la définition de x comme suit:
let x =
let r = ref None in
fun () ->
match !r with
| None ->
let v = 3 + 3 in r := Some v; v
| Some v ->
vOn vous demande de définir un type 'a future, représentant les calculs différés de type 'a, ainsi que les fonctions suivantes:
(* Créer un calcul différé à partir d'une fonction *)
val offun : (unit -> 'a) -> 'a future
(* Créer un calcul différé à partir d'une valeur *)
val ofval : 'a -> 'a future
(* Force l'évaluation d'un calcul différé *)
val force : 'a future -> 'a
(* Retourne si un calcul différé a déjà été évalué *)
val isval : 'a future -> boolDéposer le fichier wlist.ml :
On se propose maintenant de définir une structure de donnée pour les listes (potentiellement) infinies. On rappelle ci-dessous le type des listes:
On pourrait imaginer définir la liste de tous les entiers naturels comme suit:
Cependant, OCaml étant un langage d’évaluation stricte, ce dernier essaie de construire intégralement la liste, ce qui ne peut que mal terminer dans un monde fini:
Une technique pour coder les listes infinies est d’utiliser l’évaluation retardée afin de suspendre l’évaluation de cette dernière, par exemple en suspendant l’évaluation de la liste à chaque fois que l’on accède/retire sa tête.
En vous aidant de la définition de la une structure de donnée 'a wlist ci-dessous, vous implémenterez les fonctions suivantes:
(* Type des listes potentiellement infinies (c'est-à-dire aussi
* bien finies que infinies. *)
type 'a wlist = Nil | Cons of 'a * (unit -> 'a wlist)
(* La liste infinie vide *)
val nil : 'a wlist
(* cons x s = ajoute l'élément `x` en tête de `s` *)
val cons : 'a -> (unit -> 'a wlist) -> 'a wlist
(* cons x = la liste infinie constante `[x; x; ...]` *)
val const : 'a -> 'a wlist
(* iter f x = la liste infinie `[x; f x; f^2 x; ...]` *)
val iter : ('a -> 'a) -> 'a -> 'a wlist
(* oflist s = la liste infinie à partir de la liste `s` *)
val oflist : 'a list -> 'a wlist
(* observe s = retourne la tête et la queue de `s`.
* Retourne `None` si la liste est vide *)
val observe : 'a wlist -> ('a * 'a wlist) option
(* filter p s = la liste infinie `[x | x \in s & p x]` *)
val filter : ('a -> bool) -> 'a wlist -> 'a wlist
(* map f s = la liste infinie `[f x | x \in s]` *)
val map : ('a -> 'b) -> 'a wlist -> 'b wlist
(* combine s1 s2 = la liste infinie `[(x, y) | x \in s1, y \in s2]` *)
val combine : 'a wlist -> 'b wlist -> ('a * 'b) wlist
(* drop i s = la liste infinie obtenue en enlevant les `i`
* premiers éléments de `s`. *)
val drop : int -> 'a wlist -> 'a wlist
(* fold f s i x = comme `List.fold_lefti` mais s'arrête au bout
* de `i` étapes, c'est-à-dire, si `s` = [s0; s1; ...], alors
* fold f s i x = f i si (f ... (f 1 s1 (f 0 s0 x)) ...).
*
* Si `i` est strictement négatif, épuise toute la liste. *)
val fold : (int -> 'a -> 'b -> 'b) -> 'a wlist -> int -> 'b -> 'bQue dire de filter (fun x -> x < 0) (const 0) ? Pourquoi ?
Déposer le fichier ksnapsack.ml :
La programmation dynamique est une méthode algorithmique pour résoudre des problèmes d’optimisation. Elle consiste à résoudre un problème en le décomposant en sous-problèmes, puis à résoudre les sous-problèmes, des plus petits aux plus grands en stockant les résultats intermédiaires. Un cas particulier de programmation dynamique est la mémoïsation ou programmation dynamique descendante où un problème est résolu par une fonction récursive et où les résultats de cette dernière sont conserver d’un appel à l’autre – ceci permetttant d’accumuler les résultats déjà établis pour éviter de les recalculer ultérieurement.
Nous donnons ci-dessous une implémentation de la fonction de Fibonacci avec la technique de mémoïsation:
let fibonacci n =
if n < 0 then 0 else
let mem =
Array.init (n+1) (fun i -> if i < 2 then 1 else -1)
in
let rec aux n =
if mem.(n) >= 0 then mem.(n) else
let v = aux (n-1) + aux (n-2) in
mem.(n) <- v; v
in aux nOn vérifiera bien qu’un appel à fibonacci (n+2) ne calculera qu’une fois fibonacci n.
On s’intéresse ici à résoudre le problème du sac à dos grâce à la technique de mémoïsation. On suppose que l’on possède \(n\) objets et on note respectivement \(v_i\) et \(p_i\), pour \(i \in { 1 .. n }\), la valeur et le poids de l’objet \(i\). On suppose qu’on possède également un sac à dos de capacité \(c\). Le problème est de remplir le sac à dos tel que la somme des valeurs des objets soit maximale, c’est-à-dire de trouver \({ x_i \in { 0, 1 }}_{1 \le i \le n}\) tels que \(\sum_{i = 1}^{n} x_i p_i \le c\) et \(\sum_{i = 1}^{n} x_i v_i\) soit maximal.
On note \(T(i, j)\) la valeur maximale pouvant être atteinte avec les \(i\) premiers objets et une capacité \(j\). Alors, on a la relation de récurrence suivante:
\[ \left\{ \begin{aligned} T(0, j) &= 0 \\ T(i+1, j) &= \max \{ T(i, j), T(i, j-p\_{i+1}) + v_{i+1}\} & \text{(si $p_{i+1} \le j$)} \\ T(i+1, j) &= T(i, j) & \text{(sinon).} \end{aligned} \right. \]
On vous demande de:
Déduire de la définition de \(T\) une fonction récursive knapsack : (int * int) array -> int -> int telle que knapsack vps c calcule la valeur maximale qui peut être emporté avec un sac à dos de capacité c, où vps est la liste des couples (valeur, poids) des objets à disposition.
De modifier ksnapsack afin qu’une solution pour \(T(i, j)\) ne soit calculée qu’une seule fois; ceci en se servant d’une technique similaire à celle utilisée, ci-dessus, pour la fonction de Fibonacci. Vous pourrez, par exemple, utiliser une matrice (tableau de tableaux) de taille \(n \times c\) ou une table de hachage.