Dans ce TD, nous allons voir comment utiliser grapheX (le paquet permettant de gérer les graphes) en réalisant la programmation d'un type particulier de graphe, où les sommets représentent des points dans le plan. On peut alors considérer la distance euclidienne entre deux sommets.

Nous travaillerons à cet effet sur des exemples concrets, à savoir l'ensemble des villes et des villages d'un pays. Nous prendrons comme exemple la France et Mayotte. Attention, pour des problèmes de quota disque, les fichiers sont déjà installés sur les stations de l'enseignement et il n'est pas nécessaire de les mettre sur votre compte. Néanmoins, pour ceux qui travaillent sur leur ordinateur personnel, vous pouvez les placer dans votre répertoire TD6 .

Si vous désirez travailler (en dehors du TD) sur d'autres pays ou comprendre le contenu de ces fichiers de données, vous pouvez vous rendre à l'adresse suivante.

grapheX

grapheX est un paquet développé par F. Morain et par P. Chassignet permettant de travailler sur les graphes. Pour de plus amples informations, vous pouvez vous référer au polycopié du cours. Nous aurons besoin d'utiliser ce paquet tout au long du TD, il vous faut donc l'installer. Pour cela téléchargez l'archive de grapheX sur la page du cours. (Pour les utilisateurs de windows téléchargez simplement grapheX.jar et placez le dans le répertoire INF431) Ensuite, décompressez l'archive, soit à l'aide de l'explorateur de fichier, soit en utilisant la ligne de commande tar -zxvf grapheX-2.1.tgz. Vous devez avoir maintenant un répertoire grapheX-2.1. Placez ce répertoire dans votre répertoire INF431 (la racine pour eclipse). Pour compiler un programme utilisant grapheX vous avez deux possibilités :

1. Vous utilisez eclipse. Un petit film est à votre disposition ici pour vous montrer comment réaliser cette opération. Sinon, dans votre projet, dans la fenêtre de gauche vous avez votre projet TD6. Cliquez avec le bouton droit sur le projet et choisissez Properties. Ensuite, choisissez Java Build Path et l'onglet Libraries et enfin cliquez sur add External jar et choisissez le fichier grapheX.jar.
2. Vous n'utilisez pas eclipse. En restant dans votre répertoire TD6, il suffit de compiler vos programme par la commande javac -cp ../grapheX-2.1/grapheX.jar:. *.java et l'exécution est faite par la commande java -cp ../grapheX-2.1/grapheX.jar:. Main, où on suppose que ../grapheX-2.1/grapheX.jar est le chemin d'accès au fichier grapheX.jar et Main est le nom de la classe à lancer.

Le graphe des villes

Nous allons donc représenter des graphes dont les sommets sont des villes. Pour cela on vous fournit une implémentation de la classe Ville et la représentation d'un ensemble de Ville.

Téléchargez les fichiers Ville.java et EnsembleVille.java permettant de lire les fichiers de données et de représenter les villes. Ces deux fichiers contiennent deux classes qui vous seront utiles :

• Ville : Cette classe représente une ville, c'est-à-dire son nom et ses coordonnées (latitude, longitude). De plus comme il y a de nombreuses villes qui portent le même nom, on adjoint à cette classe un identifiant unique (qui se trouve dans les fichiers de données). Une ville est un sommet du graphe, notre classe Ville étend donc la classe Identifiable du package grapheX fourni sur la page du cours. La classe Identifiable est une superclasse pour représenter des éléments ayant un identifiant unique. Nous utiliserons donc naturellement comme identifiant l'identifiant de la Ville. Ainsi, la classe Ville peut se résumer à l'interface publique suivante que vous aurez besoin d'utiliser dans le TD.

  public class Ville extends Identifiable {
    // Permet l'affichage de la ville par un appel a System.out.println(ville);
    public String toString();
  
    // Calcule la distance en metres entre la ville courante et dest
    public double distance(Ville dest);
  
  }
  

• EnsembleVille : Cette classe contient juste un ensemble de Ville et quelques méthodes utiles :

  public class EnsembleVille {
    // Charge les villes dans le fichier nom
    EnsembleVille(String nom) ...
  
    // Nombre de villes dans l'ensemble
    public int size() ...
  
    // Renvoie la ieme Ville de l'ensemble
    public Ville getVille(int i) ...
  
  }
  

Vous pouvez exécuter la classe EnsembleVille qui contient une méthode main chargeant l'ensemble des villes de Mayotte. Vous serez peut-être amenés à modifier dans cette méthode main le chemin d'accès au fichier mf.txt.

Vers des sommets géométriques

Nous allons maintenant créer la classe GrapheGeometrique permettant de représenter un graphe. Le paquetage grapheX définit une classe abstraite GrapheGenerique. Nous allons en écrire une implémentation. Pour cela, il faut redéfinir a minima les méthodes abstraites présentes dans la classe GrapheGenerique. Nous utiliserons donc le squelette suivant. Si vous utilisez eclipse, il n'est pas nécessaire de copier coller le code et eclipse peut créer cette classe de manière automatique. Il vous suffit de réaliser l'opération décrite dans ce petit film. Il vous suffira simplement de rajouter le champ LinkedList<Ville> sommets; après cette création.

import java.util.Collection;
import java.util.LinkedList;

import grapheX.Arc;
import grapheX.GrapheGenerique;

public class GrapheGeometrique extends GrapheGenerique<Ville> {
  LinkedList<Ville> sommets;

  public GrapheGeometrique() {
    // TODO Auto-generated constructor stub
  }

  @Override
  public int taille() {
    // TODO Auto-generated method stub
    return 0;
  }

  @Override
  public void ajouterSommet(Ville s) {
    // TODO Auto-generated method stub

  }

  @Override
  public Collection<Ville> sommets() {
    // TODO Auto-generated method stub
    return null;
  }

  @Override
  public void ajouterArc(Ville s, Ville t, int val) {
    // TODO Auto-generated method stub

  }

  @Override
  public boolean existeArc(Ville s, Ville t) {
    // TODO Auto-generated method stub
    return false;
  }

  @Override
  public Collection<Arc<Ville>> voisins(Ville s) {
    // TODO Auto-generated method stub
    return null;
  }

  @Override
  public int valeurArc(Ville s, Ville t) {
    // TODO Auto-generated method stub
    return 0;
  }

  @Override
  public void enleverArc(Ville s, Ville t) {
    // TODO Auto-generated method stub

  }

}

1. Complétez le constructeur GrapheGeometrique pour qu'il initialise la liste des sommets.
2. Complétez les méthodes public int taille(), public void ajouterSommet(Ville s) et public Collection<Ville> sommets(). On notera que LinkedList implémente Collection. Testez votre programme à l'aide de la méthode suivante :

     public static void test() {
       // le main prend le fichier mf.txt et affiche les villes
       EnsembleVille ens = new EnsembleVille("/users/profs/info/rossin/mf.txt");
   
       // On construit un graphe a partir des 10 premieres villes
       GrapheGeometrique g = new GrapheGeometrique();
       for (int i = 0; i < 10; i++) {
         g.ajouterSommet(ens.getVille(i));
       }
   
       Collection<Ville> villes = g.sommets();
       System.out.println("Le graphe est de taille "+g.taille());
       for (Ville s:villes)  {
         System.out.println(s);
       }
     }
   

   Vous devez obtenir le résultat suivant :

   Le graphe est de taille 10
   Accua	Latitude: -12.7225	Longitude: 45.0563889
   Acoua	Latitude: -12.7225	Longitude: 45.0563889
   Andrema	Latitude: -12.6786111	Longitude: 45.0977778
   Apandzo	Latitude: -12.8305556	Longitude: 45.1302778
   Bambo Est	Latitude: -12.9261111	Longitude: 45.1738889
   Bambo Ouest	Latitude: -12.9219444	Longitude: 45.0872222
   Bandraboua	Latitude: -12.7016667	Longitude: 45.1205556
   Bandrajou	Latitude: -12.7452778	Longitude: 45.2186111
   Bandrani	Latitude: -12.845	Longitude: 45.1019444
   Bandrele	Latitude: -12.9066667	Longitude: 45.1913889
   

   Vous pouvez aussi tester à l'aide de la fonction suivante et en téléchargeant la classe MaFenetre.java.

     public static void test2() {
       // le main prend le fichier mf.txt et affiche les villes
       EnsembleVille ens = new EnsembleVille("/users/profs/info/rossin/mf.txt");
   
       GrapheGeometrique g = new GrapheGeometrique();
       for (int i = 0; i < ens.size(); i++)
         g.ajouterSommet(ens.getVille(i));
   
       MaFenetre f = new MaFenetre();
       f.setGraphe(g);
     }
   

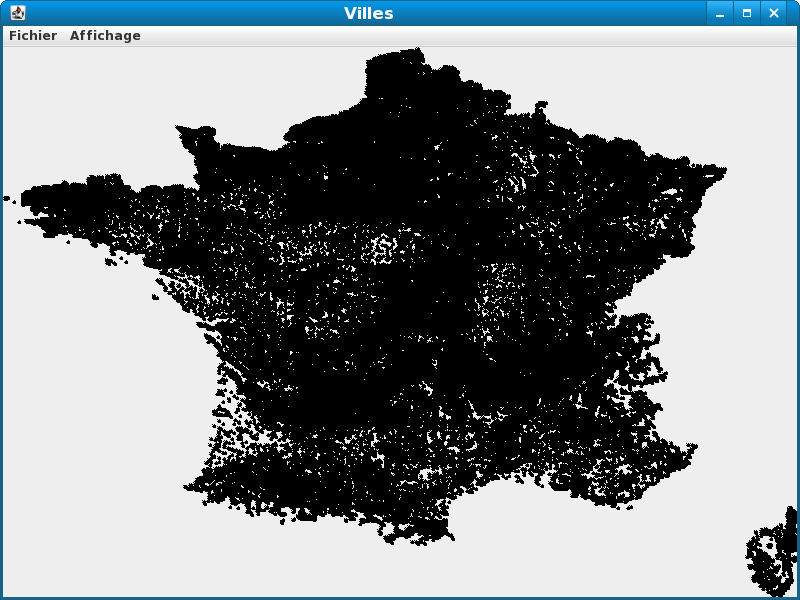
   Vous obtiendrez le résultat suivant : Vous pouvez alterner l'affichage des noms des villes en utilisant le menu d'affichage.

   

   Si vous utilisez le fichier fr.txt au lieu de mf.txt vous obtiendrez la carte :

   

Où on ajoute les arêtes

3. Les arêtes sont vues comme un ensemble (indicé par les villes d'origine) d'ensembles (indicés par les villes destinations) d'arêtes. On munira donc la classe GrapheGeometrique d'un champ HashMap<Ville,HashMap<Ville,Arc<Ville>>> aretes. La première ville correspond à l'origine de l'arc et la seconde correspond à la ville destination de l'arc associé dans le HashMap<Ville,Arc<Ville>>>. On rappelle que la classe Arc est définie dans le package grapheX et définit un arc orienté d'un sommet origine vers un sommet destination. Complétez les méthodes :
   • Le constructeur GrapheGeometrique pour qu'il initialise la table de hachage des arêtes.
   • ajouterSommet(Ville s) pour que cette méthode associe au sommet s une nouvelle HashMap<Ville,Arc<Ville>> vide pour la liste des arêtes.
   • ajouterArc(Ville s, Ville t, int val)
   • existeArc(Ville s, Ville t)
   • voisins(Ville s)
   Vous pouvez tester le programme à l'aide de la méthode suivante :

     public static void test3() {
       EnsembleVille ens = new EnsembleVille("/users/profs/info/rossin/mf.txt");
   
       GrapheGeometrique g = new GrapheGeometrique();
       for (int i = 0; i < ens.size(); i++)
         g.ajouterSommet(ens.getVille(i));
   
       for (int i = 0; i < ens.size(); i++)
         for (int j = i+1; (j < i+3 && j < ens.size()); j++)
           g.ajouterArc(ens.getVille(i),ens.getVille(j),i);
       // On met la valeur i aux arcs car cette valeur est utilise par le programe pour determiner la couleur
       // des arcs
   
       for (Arc<Ville> a:g.voisins(ens.getVille(0)))
         System.out.println(a.origine()+" -- "+a.destination());
       System.out.println(g.existeArc(ens.getVille(0), ens.getVille(1)));
       System.out.println(g.existeArc(ens.getVille(0), ens.getVille(3)));
     }
   

   Vous devez obtenir :

   Accua	Latitude: -12.7225	Longitude: 45.0563889 -- Andrema	Latitude: -12.6786111	Longitude: 45.0977778
   Accua	Latitude: -12.7225	Longitude: 45.0563889 -- Acoua	Latitude: -12.7225	Longitude: 45.0563889
   true
   false
   

   De manière graphique en utilisant la méthode suivante :

     public static void test4() {
       EnsembleVille ens = new EnsembleVille("/users/profs/info/rossin/mf.txt");
   
       GrapheGeometrique g = new GrapheGeometrique();
       for (int i = 0; i < ens.size(); i++)
         g.ajouterSommet(ens.getVille(i));
   
       for (int i = 0; i < ens.size(); i++)
         for (int j = i+1; (j < i+3 && j < ens.size()); j++)
           g.ajouterArc(ens.getVille(i),ens.getVille(j),i);
       // On met la valeur i aux arcs car cette valeur est utilise par le programe pour determiner la couleur
       // des arcs
   
       MaFenetre f = new MaFenetre();
       f.setGraphe(g);
     }
   

   Vous obtenez le résultat :

   

4. Complétez les méthodes :
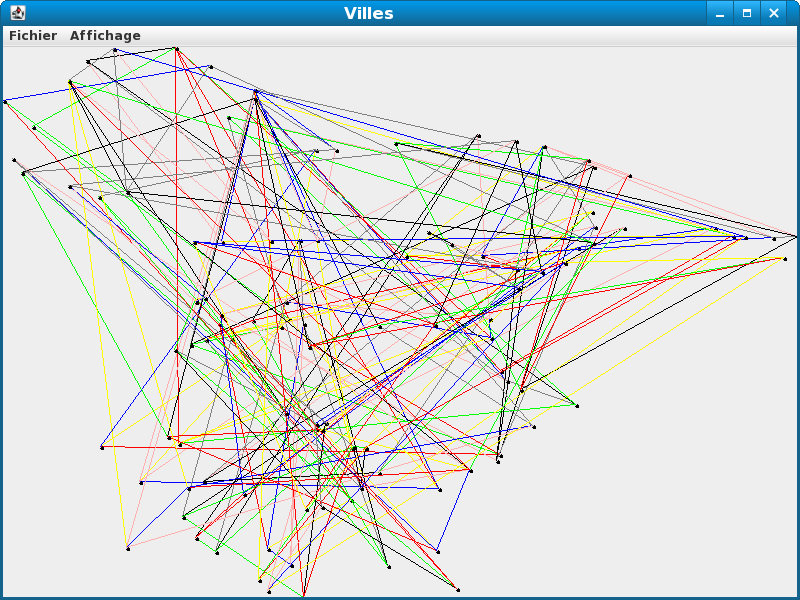
   • valeurArc(Ville s, Ville t) : On produira une erreur si l'arc n'existe pas.
   • enleverArc(Ville s, Ville t) : On choisira sciemment de ne rien faire si l'arc n'existe pas.
   Vous pouvez tester votre programme à l'aide de la méthode suivante :

     public static void test5() {
       EnsembleVille ens = new EnsembleVille("/users/profs/info/rossin/mf.txt");
   
       GrapheGeometrique g = new GrapheGeometrique();
       for (int i = 0; i < ens.size(); i++)
         g.ajouterSommet(ens.getVille(i));
   
       for (int i = 0; i < ens.size(); i++)
         for (int j = i+1; (j < i+3 && j < ens.size()); j++)
           g.ajouterArc(ens.getVille(i),ens.getVille(j),i);
   
       for (int i = 0; i < ens.size(); i++)
         if (i+2 < ens.size())
           g.enleverArc(ens.getVille(i),ens.getVille(i+2));
   
       MaFenetre f = new MaFenetre();
       f.setGraphe(g);
   
       System.out.println(g.existeArc(ens.getVille(0), ens.getVille(1)));
       g.enleverArc(ens.getVille(0), ens.getVille(1));
       g.enleverArc(ens.getVille(0), ens.getVille(1));
       System.out.println(g.existeArc(ens.getVille(0), ens.getVille(1)));
       System.out.println(g.existeArc(ens.getVille(0), ens.getVille(2)));
       System.out.println(g.valeurArc(ens.getVille(2), ens.getVille(3)));
       System.out.println(g.valeurArc(ens.getVille(0), ens.getVille(2)));
     }
   

   Vous devez obtenir le résultat suivant :

   true
   false
   false
   2
   Exception in thread "main" java.lang.Error: Arc inexistant ...
   

   

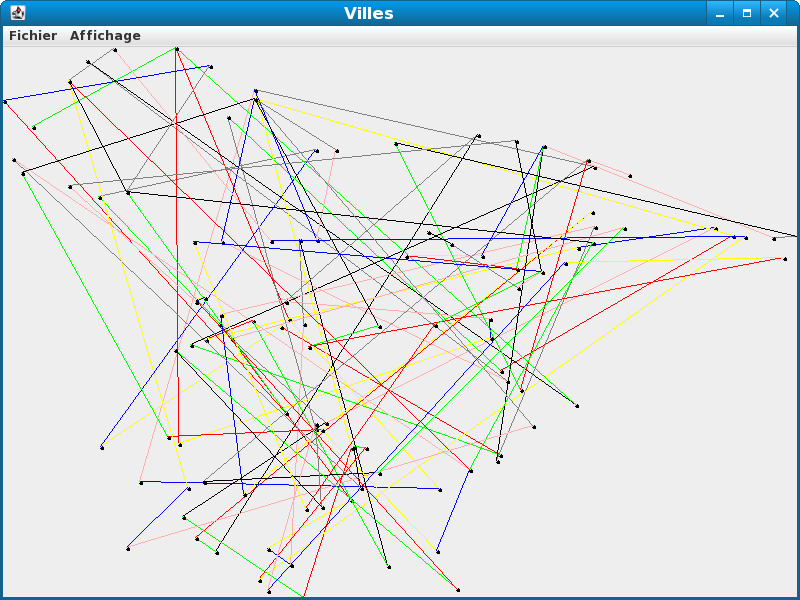
Graphe de proximité

5. On va maintenant coder un graphe de proximité. Intuitivement, on va supposer que l'on possède un petit avion avec une réserve d'essence très limitée qui ne nous permet de relier que des villes à distance plus petite qu'une certaine donnée distEssence. Ecrivez dans la classe GrapheGeometrique une méthode (en temps quadratique) euclidien(double distEssence) qui à partir des sommets du graphe, obtenus par sommets(), ajoute tous les arcs entre des sommets à une distance plus petite que distEssence (on mettra 0 comme valeur pour les arcs que l'on rajoute). On pourra utiliser la méthode double distance(Ville dest) de la classe Ville qui donne la distance entre la ville courante et la ville dest. Il s'agit d'un graphe non orienté et finalement chaque arc aura son réciproque.
Vous pouvez tester votre programme à l'aide de la méthode suivante :

  public static void test6() {
    EnsembleVille ens = new EnsembleVille("/users/profs/info/rossin/mf.txt");

    GrapheGeometrique g = new GrapheGeometrique();
    for (int i = 0; i < ens.size(); i++)
      g.ajouterSommet(ens.getVille(i));
    g.euclidien(2000);
    MaFenetre f = new MaFenetre();
    f.setGraphe(g);
  }

Vous obtenez :



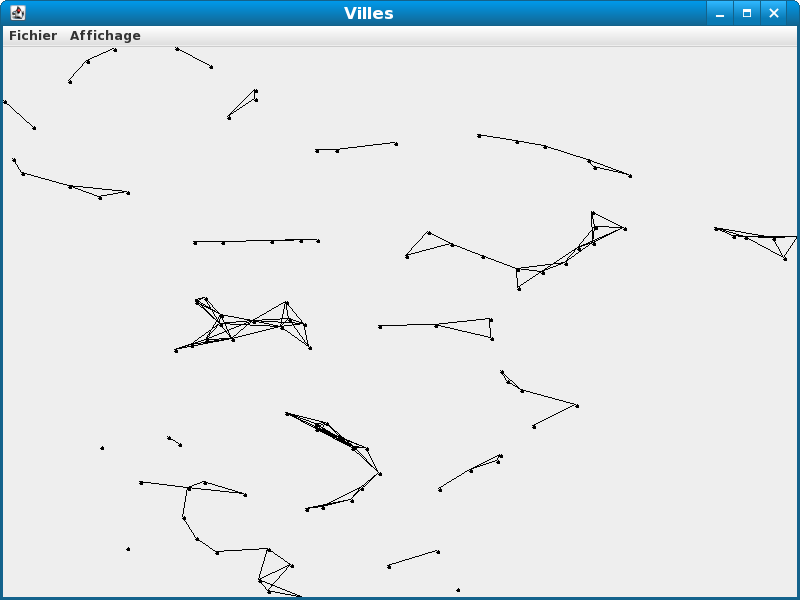
Qu'obtenez-vous avec une distance de 4000 mètres ? Il est fortement déconseillé d'essayer avec la France car alors le temps de construction avoisinerait l'heure. En effet, l'algorithme est ici quadratique en le nombre de villes (plus de 75000 pour la France). Vous pouvez en revanche prendre un sommet sur 30, par exemple avec le programme suivant :

  public static void test7() {
    // le main prend le fichier fr.txt et affiche les villes
    EnsembleVille ens = new EnsembleVille("/users/profs/info/rossin/fr.txt");

    GrapheGeometrique g = new GrapheGeometrique();
    for (int i = 0; i < ens.size()/30; i++)
      g.ajouterSommet(ens.getVille(i*30));
    g.euclidien(25000);
    MaFenetre f = new MaFenetre();
    f.setGraphe(g);
  }

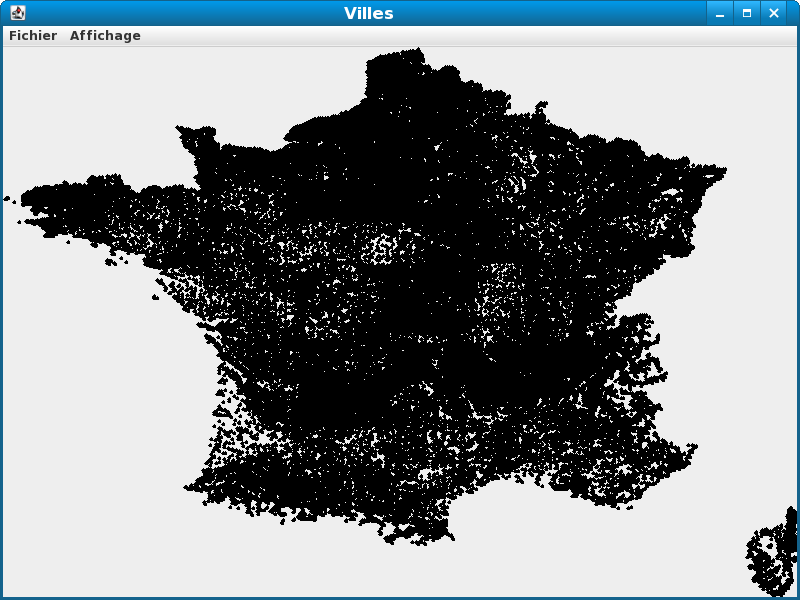
Vous obtenez :



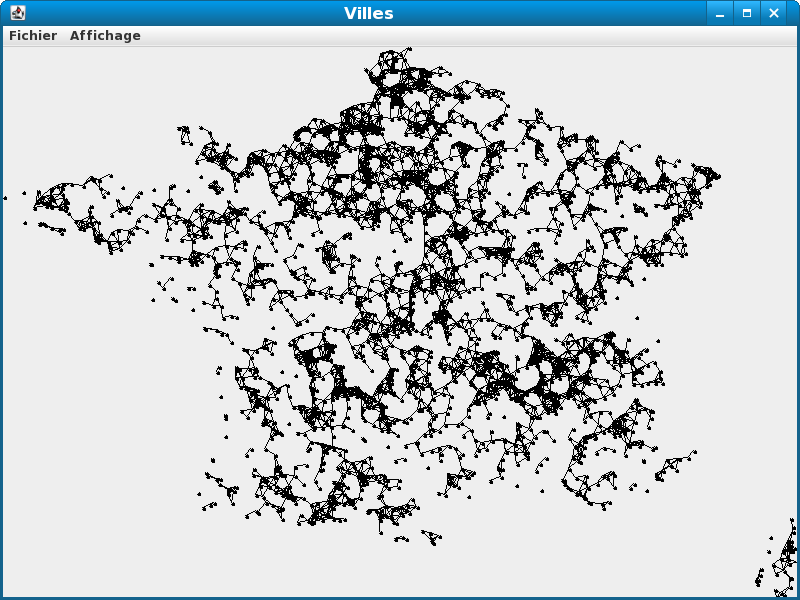
Composantes connexes

Vous pouvez voir sur l'exemple que les villes ne sont pas toutes reliées entre elles. Chaque ensemble relié est appelé une composante connexe du graphe. Vous verrez la semaine prochaine comment calculer ces composantes de manière efficace. Cette semaine, nous allons utiliser une méthode plus lente pour le faire. Nous allons construire un graphe en parallèle du premier contenant les mêmes sommets mais représentant un ensemble d'arbres (une forêt). On peut voir chaque arbre comme un graphe où, pour chaque sommet s, on a soit un unique arc d'origine s (vers son père dans l'arbre) soit aucun (s est alors la racine de l'arbre). De plus les graphes considérés n'ont pas de cycle. On appellera alors puits de s ou racine de s, le sommet t tel qu'il existe une suite d'arcs reliant s à t (s->s1->s2->...->t) et qu'il n'existe pas d'arc d'origine t. Le principe de l'algorithme est le suivant :
• Au début, la nouveau graphe n'a pas d'arête.
• Pour chaque arc de s à t dans le graphe d'origine, si les puits correspondant à s et t dans le nouveau graphe sont différents alors on accroche le puits de l'un des sommets (puits de s par exemple) à l'autre (puits de t) dans le nouveau graphe.
Pour coder ce graphe, nous utiliserons la classe GrapheGeometrique que vous venez d'écrire. Pour programmer la méthode ci-dessus, nous avons besoin de deux opérations sur les arbres.
• Relier deux puits ensembles. Il suffit pour cela d'ajouter un arc orienté entre un puits et l'autre.
• Décider si deux sommets ont le même puits. Il suffit pour cela de suivre les arcs en partant de chacun des sommets et voir si le sommet final est le même pour les deux.
6. Programmez une méthode Ville calculPuits(Ville s) qui calcule le puits du sommet s. On suppose dans cette question que le graphe est une forêt représentée comme ci-dessus, i.e. chaque sommet est l'origine d'au plus un arc. Vous aurez besoin dans cette question de retrouver le père d'un sommet dans l'arbre, c'est-à-dire trouver l'unique Ville présente dans une Collection<Arc<Ville>>. Vous pouvez vous aider de la méthode suivante:

   Arc<Ville> premierArc(Collection<Arc<Ville>> c) {
     for (Arc<Ville> a:c)
       return a;
     return null;
   }
   

   Vous pouvez tester votre méthode à l'aide de la fonction suivante :

       public static void test8() {
     EnsembleVille ens = new EnsembleVille("/users/profs/info/rossin/mf.txt");
   
     GrapheGeometrique g = new GrapheGeometrique();
       for (int i = 0; i < ens.size(); i++)
           g.ajouterSommet(ens.getVille(i));
   
       for (int i = 0; i < ens.size()/2; i++)
           g.ajouterArc(ens.getVille(i),ens.getVille(i+1),i);
   
       System.out.println(ens.getVille(0)+ " ---> "+g.calculPuits(ens.getVille(0)));
       System.out.println(ens.getVille(70)+ " ---> "+g.calculPuits(ens.getVille(70)));
   
       }
   

   Vous devez obtenir :

   Accua	Latitude: -12.7225	Longitude: 45.0563889 ---> Malamani	Latitude: -12.9169444	Longitude: 45.1563889
   Manyassini	Latitude: -12.8888889	Longitude: 45.1411111 ---> Manyassini	Latitude: -12.8888889	Longitude: 45.1411111
   

7. Programmez ensuite une méthode void fusion(Ville s,Ville t) qui étant donnés deux sommets calcule les puits puitss et puitst associés. Si ces puits sont différents alors on ajoute un arc de puitss à puitst. Vous pouvez tester avec la fonction suivante :

       public static void test9() {
       EnsembleVille ens = new EnsembleVille("/users/profs/info/rossin/mf.txt");
   
       GrapheGeometrique g = new GrapheGeometrique();
       for (int i = 0; i < ens.size(); i++)
           g.ajouterSommet(ens.getVille(i));
   
       for (int i = 0; i < ens.size()/2; i++)
           g.ajouterArc(ens.getVille(i),ens.getVille(i+1),i);
   
       System.out.println(ens.getVille(0)+ " ---> "+g.calculPuits(ens.getVille(0)));
       System.out.println(ens.getVille(70)+ " ---> "+g.calculPuits(ens.getVille(70)));
       g.fusion(ens.getVille(0),ens.getVille(70));
       System.out.println(ens.getVille(0)+ " ---> "+g.calculPuits(ens.getVille(0)));
       System.out.println(ens.getVille(70)+ " ---> "+g.calculPuits(ens.getVille(70)));
       }
   

   Vous devez obtenir :

   Accua	Latitude: -12.7225	Longitude: 45.0563889 ---> Malamani	Latitude: -12.9169444	Longitude: 45.1563889
   Manyassini	Latitude: -12.8888889	Longitude: 45.1411111 ---> Manyassini	Latitude: -12.8888889	Longitude: 45.1411111
   Accua	Latitude: -12.7225	Longitude: 45.0563889 ---> Manyassini	Latitude: -12.8888889	Longitude: 45.1411111
   Manyassini	Latitude: -12.8888889	Longitude: 45.1411111 ---> Manyassini	Latitude: -12.8888889	Longitude: 45.1411111
   

8. Programmez enfin une méthode GrapheGeometrique composanteConnexe() dans la classe GrapheGeometrique qui à partir du graphe courant, calcule puis renvoie le graphe qui décrit la forêt. Cette méthode ne modifiera pas le graphe d'origine. On affectera aux arcs de ce graphe la valeur 2 pour les dessiner dans une autre couleur. Vous pouvez déjà tester votre programme à l'aide de la méthode suivante :

       public static void test10() {
       EnsembleVille ens = new EnsembleVille("/users/profs/info/rossin/mf.txt");
   
       GrapheGeometrique g = new GrapheGeometrique();
       for (int i = 0; i < ens.size(); i++)
           g.ajouterSommet(ens.getVille(i));
       g.euclidien(2000);
       GrapheGeometrique g2  = g.composanteConnexe();
       MaFenetre f = new MaFenetre();
       f.setGraphe(g);
       MaFenetre f2 = new MaFenetre();
       f2.setGraphe(g2);
   
       }
   
   

   Vous devez obtenir le résultat suivant :

   

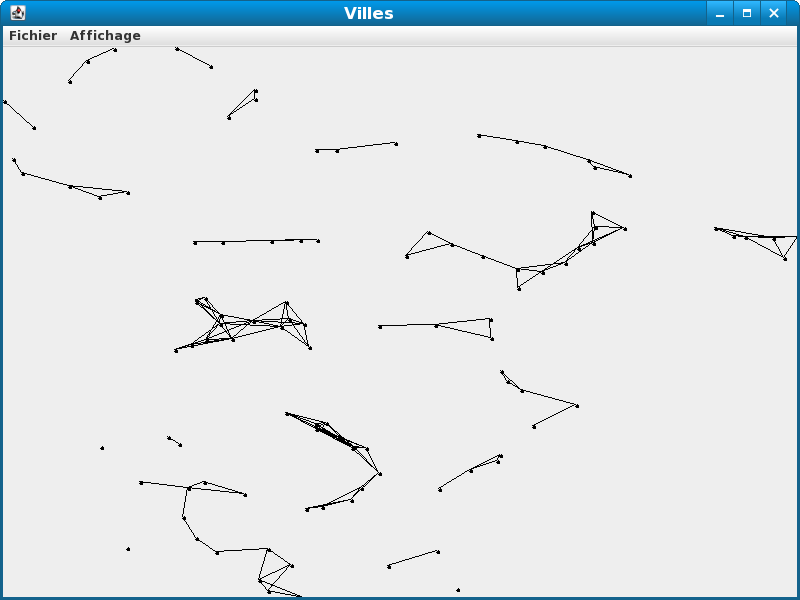
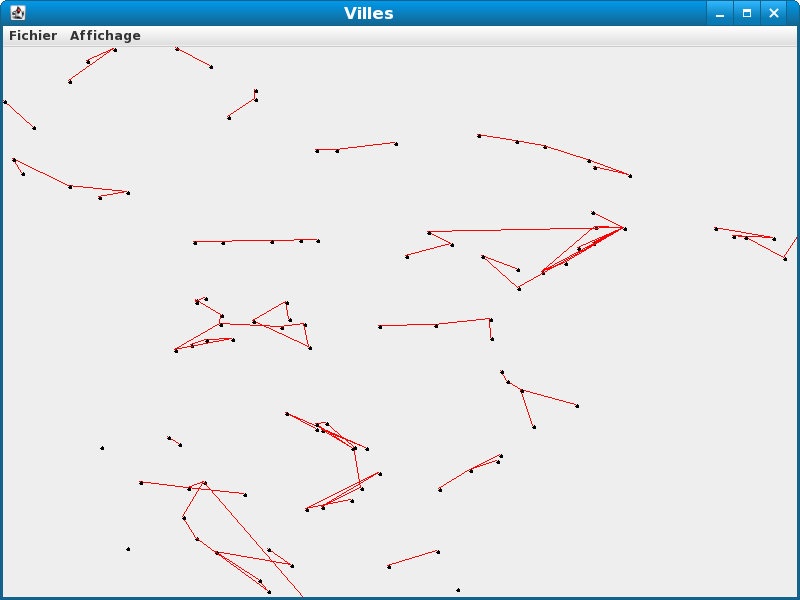
   Notez que sur le second graphe, nous avons des arbres.

9. Écrire maintenant une méthode void colorieComposantesConnexes() qui, au lieu de renvoyer le second graphe, devra colorier les arcs du premier graphe avec des valeurs dépendant des composantes auxquelles ils appartiennent. Une méthode (non optimale) pour réaliser cette opération est de calculer la forêt F décrivant les composantes connexes. Ensuite, on va rechercher l'ensemble des puits, c'est-à-dire l'ensemble des sommets qui n'ont pas d'arc sortant et leur attribuer une couleur. On pourra stocker cette couleur dans une table HashMap<Ville,Integer>. Finalement, on parcourt l'ensemble des arcs du graphe initial et on affecte à chacun d'entre eux la couleur du puits correspondant dans la forêt. Testez avec le programme suivant :

       public static void test11() {
       EnsembleVille ens = new EnsembleVille("/users/profs/info/rossin/mf.txt");
   
       GrapheGeometrique g = new GrapheGeometrique();
       for (int i = 0; i < ens.size(); i++)
           g.ajouterSommet(ens.getVille(i));
       g.euclidien(2000);
       g.colorieComposantesConnexes();
       MaFenetre f = new MaFenetre();
       f.setGraphe(g);
       }
   

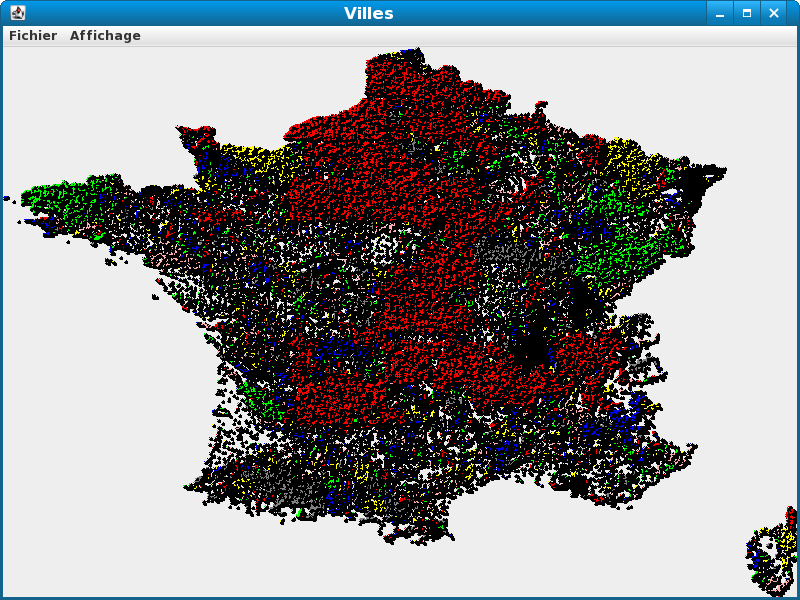
   Vous devez obtenir le résultat :

   

   En reprenant le test sur la France avec un seuil euclidien de 21000, vous obtenez :

   

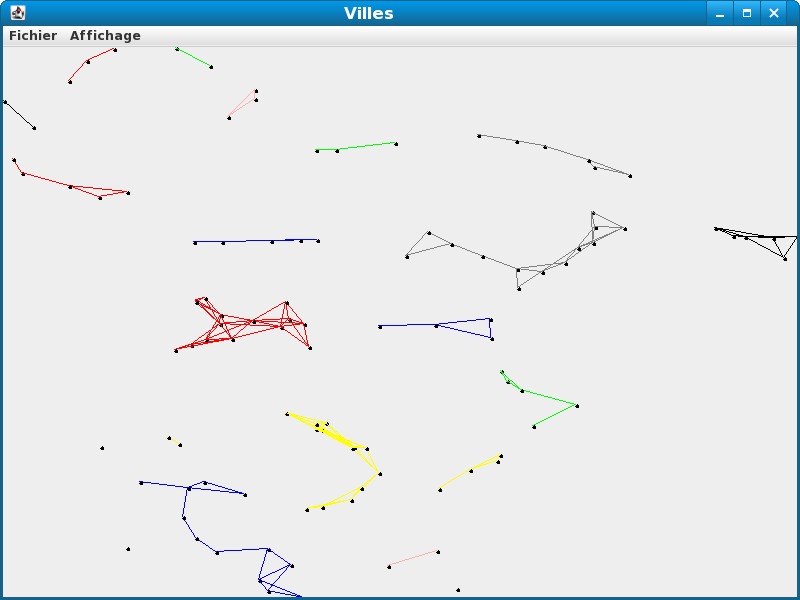
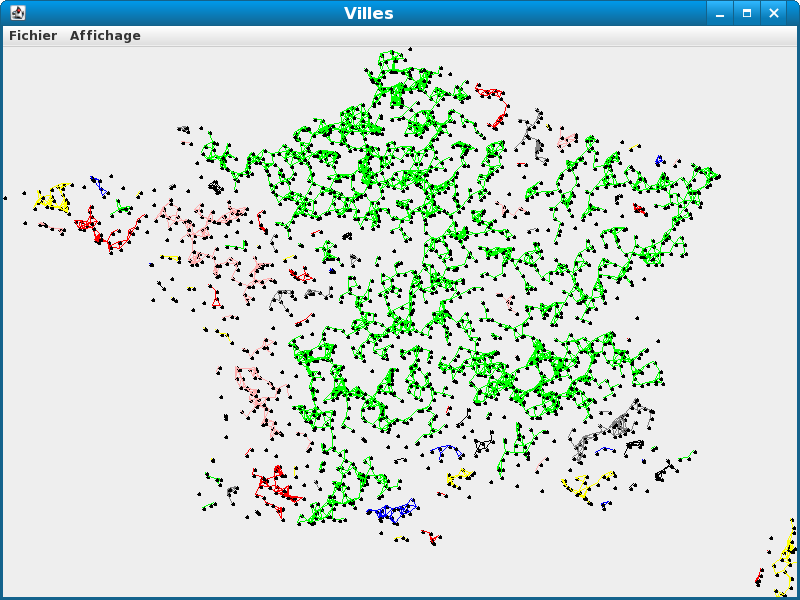
Vers une structure de données géométrique

10. Le problème dans ce TD est le calcul des arêtes du graphe euclidien. Pour pallier ce problème, il suffit de représenter les sommets dans le graphe non pas par une liste chaînée mais par un tableau dont chaque case représentera un carré de 2km par 2km par exemple. Ensuite, pour construire le graphe euclidien il suffit de rechercher les sommets voisins d'un sommet dans la même case ou dans une des cases voisines.

    Plus précisement, créez une classe GrapheEuclidien suivant le squelette suivant :

    class GrapheEuclidien extends GrapheGeometrique {
        HashMap<Integer,HashMap<Integer,LinkedList<Ville>>> listeSommets;
        int nVilles;
    
        int distance;
        double angleDistance;
    
        GrapheEuclidien(int distance) { // La distance est en metres
        double R = 6371000; // rayon de la terre
        this.distance = distance;
        // On calcule la distance en degres
        angleDistance = distance / Math.PI * 180.0 / R;
        nVilles = 0;
        listeSommets = new HashMap<Integer,HashMap<Integer,LinkedList<Ville>>>();
        }
    
        int caseX(Ville s) {
      return (int) ((s.getLongitude()+180.0)/angleDistance);
        }
    
        public int taille() {
      return nVilles;
        }
    
    
        int caseY(Ville s) {
      return (int) ((s.getLatitude()+180.0)/angleDistance);
        }
    
        public void ajouterSommet(Ville s) {
        aretes.put(s,new HashMap<Ville,Arc<Ville>>());
        nVilles++;
        // TODO A COMPLETER
    
        }
    
        public Collection<Ville> sommets() {
          // TODO A COMPLETER
          return null;
        }
    
        public void euclidien(double distEssence) {
        euclidien(); // On utilise la distance du constructeur
        }
    
        Collection<Ville> sommetsEn(int x,int y) {
          if (!listeSommets.containsKey(x))
            return java.util.Collections.emptySet();
          HashMap<Integer,LinkedList<Ville>> ll = listeSommets.get(x);
          if (!ll.containsKey(y)) return java.util.Collections.emptySet();
          return ll.get(y);
        }
    
        public void euclidien() {
          // TODO A COMPLETER
        }
    
    }
    

    Pour représenter le tableau, on utilise une double HashMap dont le premier entier représente l'abscisse de la case où doit se trouver le sommet et le second son ordonnée. Pour vous faciliter le travail nous vous donnons les méthodes qui à partir d'un sommet calculent l'abscisse et l'ordonnée de la case. Pour calculer le graphe euclidien avec une distance égale à la largeur d'une case, il suffit donc pour un sommet de calculer les coordonnées (x,y) de la case où se trouve ce sommet, et de remarquer qu'un sommet relié à celui-ci est forcément dans une des cases :
    • (x,y)
    • (x+1,y)
    • (x-1,y)
    • (x,y+1)
    • (x,y-1)
    • (x+1,y+1)
    • (x+1,y-1)
    • (x-1,y-1)
    • (x-1,y+1)
    Sur la France complète, SANS calculer les composantes connexes, vous devez pouvoir réaliser le calcul du graphe euclidien en une poignée de secondes. Si vous avez des problèmes de mémoire vous pouvez exécuter java avec l'option java -Xmx500m -Xms500m Test.java. Vous obtenez pour une distance de 4000 mètres :

    

    Vous pouvez maintenant lancer le calcul des composantes connexes et en utilisant une distance de 4000 vous obtenez le résultat suivant :