Pale machine du mardi 15 octobre 2019 (English version)

Please use the French version of this exam to submit your files. Please be careful with the question numbers when doing so.

The two exercises are independent. Be careful to upload .java files (and not .class files).

The tests that are provided are not perfect. A validated program is not necessarily correct.

You have access to the Java documentation.

Create a Java project PaleMachine, download the sources PaleMachine.tar.gz and decompress them in the sub-directory src of your project.

Exercise 1: Union and intersection

1.1 Class `Personne`

Create a class Personne that describes a person with three fields:

prenom of type String (first name);
nom of type String (last name);
age of type int.

Add to this class

a constructor Personne(String prenom, String nom, int age);
a méthod public boolean equals(Object obj) (two persons are supposed to be the same when they have the same first name, last name and age);
a method public int hashCode() (Hint: you can use the method hashCode from class String);
a method public String toString() displaying a person with that format: [ Jean Dupont, 38 ans ].

Upload your file Personne.java (using the French version).

1.2 Union and intersection

Complete the class UnionIntersection with the following two methods.

A method static LinkedList<Personne> union(LinkedList<Personne> l1, LinkedList<Personne> l2) that returns a new list containing the union of the persons contained in lists l1 and l2 and such that
1. your code uses HashSet;
2. the returned list must not contain duplicate elements (Warning: the input lists l1 and l2 may contain duplicate elements);
3. the order of elements does not matter;
4. the overall complexity of your code must be O(l1.size() + l2.size()).

A method static LinkedList<Personne> intersection(LinkedList<Personne> l1, LinkedList<Personne> l2) that returns a new list containing the intersection of the persons contained in lists l1 and l2. This method must also satisfy the requirements 1, 2, 3, 4 given for method union.

You have access to the documentation of LinkedList and HashSet.

Test your program using Test1.java. Then upload your file UnionIntersection.java (using the French version).

Exercise 2: the Stern-Brocot tree

The goal of this exercise is to build and study binary trees whose nodes contain rational numbers and whose properties will be explained in the following. As in lecture/TD 5, the empty tree is implemented with null.

2.1 Building the tree

We are given two rational numbers a_l = p_l/q_l and a_r = p_r/q_r and an integer limit > q_l, q_r. The Stern-Brocot tree associated to (a_l, a_r, limit) is built as follows:

If q_l + q_r > limit, it is empty;
Otherwise, its root contains the rational number x = (p_l + p_r) / (q_l + q_r), its left subtree is the Stern-Brocot tree associated to (a_l, x, limit) and its right subtree is the Stern-Brocot tree associated to (x, a_r, limit).

In SternBrocot.java, complete the method static SternBrocot build(pl, ql, pr, qr, limit) that returns the Stern-Brocot tree associated to (pl/ql, pr/qr, limit). We assume that pl/ql < pr/qr, that these two fractions are irreducible (numerator and denominator are relatively primed), and that pl, ql, pr, qr are nonnegative.

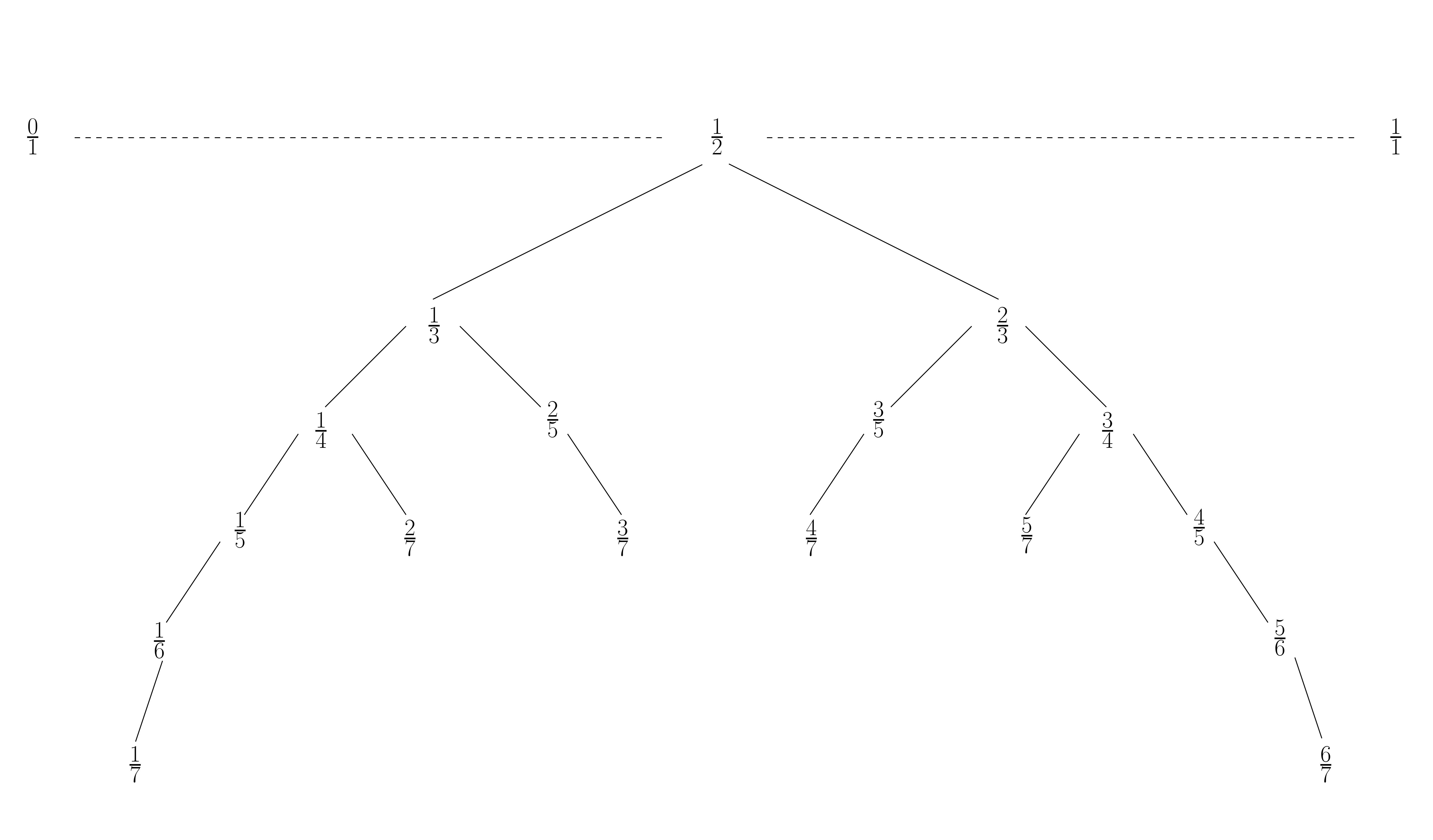
L'arbre de Stern Brocot associé à (0/1, 1/1, 7)

Figure 1. The Stern-Brocot tree associated to (0/1, 1/1, 7) obtained by calling build(0,1,1,1,7). The values 0/1 and 1/1 and the dotted lines illustrate that all rational numbers in that tree belong to the interval ]0/1,1/1[. To better visualize the tree, click here.

Test your program using Test21.java. Then upload your file SternBrocot.java (using the French version).

2.2 Size

Complete the method static int size(SternBrocot t) that returns the number of nodes in tree t.

Test your program using Test22.java. Then upload your file SternBrocot.java (using the French version).

2.3 Stern-Brocot trees are binary search trees

Stern-Brocot trees have, by construction, a structure of binary search tree, with all nodes within the interval ]p_l/q_l, p_r/q_r[ (we admit this property). To check it, complete the method static boolean isBST(SternBrocot t, int pl, int ql, int pr, int qr) that returns true if and only if

the tree t is indeed a binary search tree;
all its nodes are in ]p_l/q_l, p_r/q_r[.

Test your program using Test23.java. Then upload your file SternBrocot.java (using the French version).

2.4 Enumeration

We seek to enumerate all nodes of a given Stern-Brocot tree in increasing order, as a LinkedList<String> l whose elements are strings of the form "p/q".

Complete the method treeToList. Use an auxiliary method static void treeToList(SternBrocot t, LinkedList<String> l) if needed.

Test your program using Test24.java. Then upload your file SternBrocot.java (using the French version).

2.5 Path in the tree

We consider the Stern-Brocot tree associated to (0/1, 1/1, limit) for a given integer limit. The Stern-Brocot tree being a binary search tree, we can search for a given rational number p/q efficiently, descending either to the left or to the right subtree, and stopping when the node contains p/q (success) or when the tree is empty (failure). One can represent the path in the tree corresponding to such a search as a sequence of characters L (when we descend to the left) or R (when we descend to the right). With the tree in Figure 1, we associate to 1/3 the sequence L (success), to 2/7 the sequence LLR (success) and to 5/14 the sequence LLRR (failure).

Complete the method String path(SternBrocot t, int p, int q) that returns the string corresponding to the search of p/q. The string ends with ! if p/q belongs to t and with ? otherwise. With the tree t in Figure 1, path(t, 2, 7) returns the string "LLR!" and path(t, 5, 14) returns the string "LLRR?" (since 2/7 < 5/14 < 1/3).

Test your program using Test25.java. Then upload your file SternBrocot.java (using the French version).

2.6 From the sequence to the rational number

Complete the method fromPath that performs the reverse operation: given a string of characters L or R, it returns the corresponding rational number in a Stern-Brocot tree associated to (0/1, 1/1, limit) for a value of limit large enough for that path to reach a rational number.

Warning. Your program must not build any tree.

The rational number must be returned as an array of two integers. For instance, fromPath("RLL") returns the array {4,7}. The syntax to create a two-element array containing a and b is new int[]{a,b}.

Test your program using Test26.java Then upload your file SternBrocot.java (using the French version).

2.7 Rational approximation

Complete the method lowApprox(t, x) that takes a Stern-Brocot tree t and a real number x as input and returns the greatest element in t that is lower than or equal to x, if it exists, and null otherwise. If the result is not null we return a rational number as an array of two integers {numerator, denominator}.

Test your program using Test27.java. Then upload your file SternBrocot.java (using the French version).

2.8 Good rational approximations

In a similar way, implement a method static int[] upApprox(SternBrocot t, double x) that returns the smallest element of t that is greater than or equal to x, if its exists, and null otherwise.

Le x be a real. We say that p/q is a good rational approximation of x if p, q are relatively primed and

|x - p/q| < 1/q².
In SternBrocot.java, add a method public static void main(String[] args), in which you build the Stern-Brocot tree with limit = 100, and the you test, for 1000 randomly-chosen real numbers x ∈ [0.01, 0.99[ (use method Math.random()), that at least one of the two approximations given by lowApprox and upApprox is a good approximation.

Upload your file SternBrocot.java (using the French version).