INF411 — TD9 : Finding Nemo

Introduction

Le monde aquatique est en émoi : le petit Nemo a été enlevé ! Marin, son pauvre papa, doit partir à sa recherche. Mais l’océan est un vrai labyrinthe, peuplé de requins affamés. Sauras-tu aider Marin à retrouver Nemo le plus rapidement possible, en évitant les requins tant que faire se peut ?

Le code fourni

Ce TD repose sur une assez grande quantité de code fourni dont vous devrez consulter la documentation pour comprendre comment l’utiliser.

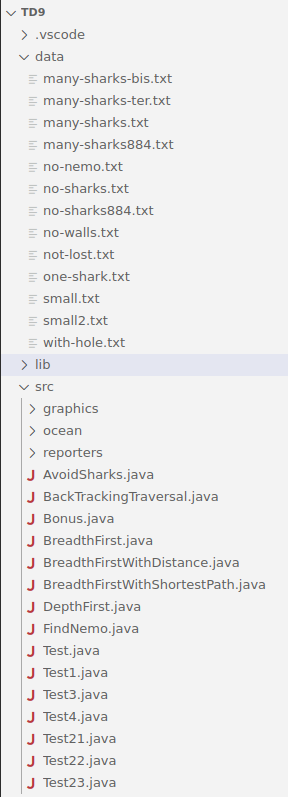
Extrayez le contenu des archives src.zip et data.zip à la racine du projet, de manière à obtenir l’arborescence de projet illustrée ci-dessous. Notez que le dossier src contient des sous-dossiers, qui correspondent à des paquets Java. Les classes à modifier et les tests se trouvent comme d’habitude à la racine de src (« paquet par défaut », default package). Les autres paquets sont utilisés pour mettre en place l’infrastructure du TD.

Le paquet ocean

Le code que vous avez à écrire utilisera les classes fournies dans le paquet ocean.

L’océan est implémenté dans la classe Ocean du paquet ocean. Nous ne considérerons que des océans correspondant à des grilles carrées 2D, mais le code fourni autorise des labyrinthes plus généraux (d’où sa complexité). La classe Ocean offre notamment des méthodes

• pour accéder au contenu d’une cellule, par exemple boolean isWall(Coordinate c),
• pour marquer une cellule, par exemple Mark setMark(Coordinate c, Mark mark) (voir aussi l’interface Mark).

Chaque cellule est identifiée par ses coordonnées en utilisant la classe Coordinate. Celle-ci fournit, entre autres, les méthodes suivantes pour manipuler les cellules :

• public boolean equals(Object o) permet (comme d’habitude) de comparer deux cellules,
• Coordinate moveTo(Direction dir) renvoie les coordonnées de la cellule voisine dans la direction dir (voir l’interface Direction).

Vous allez implémenter plusieurs algorithmes de parcours de l’océan. Chaque algorithme devra être implémenté dans une classe séparée. Toutes ces classes seront des classes dérivées de la classe abstraite Traversal. La classe Traversal spécifie (mais sans l’implémenter : c’est à vous de le faire dans les classes dérivées) une méthode traverse(Ocean ocean, Coordinate start) qui renvoie vrai s’il existe un chemin qui mène à Nemo en partant de start, faux sinon.

Les paquets graphics et reporters

Vous n’aurez pas à utiliser directement ces paquets. En bref :

• L’affichage de l’océan est codé dans le paquet graphics, dans les classes OceanCanvas et BasicOceanCanvas. Vous pouvez si vous le désirez exécuter BasicOceanCanvas : cela affichera simplement l’image en début d’énoncé.

• La classe Ocean fournit un mécanisme pour enregistrer des rapporteurs qui seront appelés automatiquement en réaction à certains événements lors de l’exploration de l’océan. Le paquet reporters implémente plusieurs rapporteurs utilisés notamment par les tests.

Pour plus de détails

Une présentation plus détaillée de la structure du code fourni est disponible ici. Par ailleurs, celui-ci est commenté en utilisant la convention JavaDoc. Vous pouvez consulter la documentation générée à partir de ces commentaires.

1. Parcours en profondeur

De tempérament obtus et inquiet, Marin a tendance à foncer droit devant sans trop réfléchir. Ce comportement, que certains pensent typique pour un poisson clown, sera modélisé par un parcours en profondeur. Afin de ne pas se perdre dans l’océan et pouvoir suivre Marin à la trace, nous adopterons une approche classique qui consiste à marquer les cellules par lesquelles nous sommes déjà passés.

Complétez la méthode traverse(Ocean ocean, Coordinate start) de la classe DepthFirst. Cette méthode doit être récursive et réaliser un parcours en profondeur de l’océan en partant de start. Chaque cellule visitée doit être marquée

• une fois par defaultMark lorsqu’on y entre,
• puis une fois lorsqu’on la quitte,
  • soit par deadEnd, si elle mène à une impasse,
  • soit par path, si elle fait partie du chemin final conduisant à Nemo.

À ce stade, on ignore les requins.

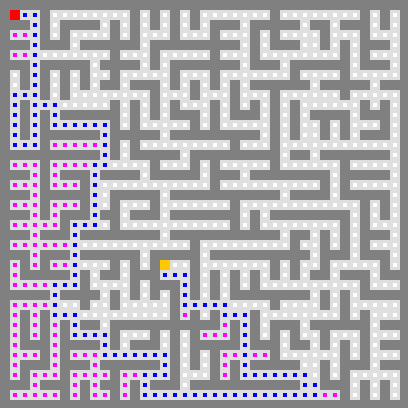
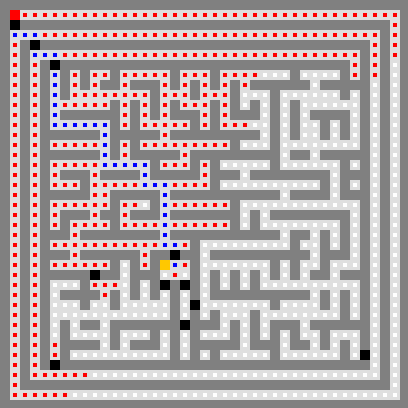
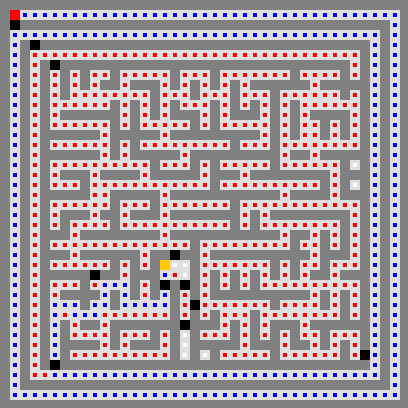
Visualisez l’exploration avec la classe DepthFirst. Le comportement attendu est illustré dans l’animation ci-dessous. Vous voyez la couleur rouge, correspondant à la marque par défaut, apparaître quand la pile d’appels se remplit et les couleurs bleu (path) et violet (deadEnd) quand elle se vide. La deuxième image montre l’état final.

Testez votre code en utilisant Test1.java, puis déposez DepthFirst.java.

2. Parcours en largeur

Bonne nouvelle ! Grâce à l’intervention de Dory, Marin va recevoir l’aide d’un banc de poissons argentés. Il va donc pouvoir les lancer dans toutes les directions à la fois, et le premier d’entre eux qui trouvera Nemo le signalera immédiatement. Ce processus sera modélisé par un parcours en largeur.

2.1 Parcours simple

Complétez la méthode traverse(...) de la classe BreadthFirst. La méthode doit implémenter le parcours en largeur de façon itérative, et s’arrêter dès que Nemo est trouvé.

Afin de réaliser le parcours en largeur, on stockera les coordonnées des cases en cours de traitement dans une file d’attente représentée par un objet de type LinkedList<Coordinate>. On commencera par mettre start dans la file. À chaque itération, on piochera une cellule au début de la file pour la traiter, puis on inspectera ses cellules voisines. Si nécessaire, on y posera la marque par défaut pour se souvenir qu’elles sont en cours de traitement et on les ajoutera en fin de file.

On ignore toujours les requins, et on ne demande pas pour l’instant de reconstituer le chemin de Marin à Nemo.

Visualisez l’exploration avec la classe BreadthFirst.

Testez votre code en utilisant Test21.java, puis déposez BreadthFirst.java.

2.2 Distances au point de départ

Complétez la méthode traverse(...) de la classe BreadthFirstWithDistance. Celle-ci doit implémenter le même parcours en largeur, mais, à la place de la marque par défaut, marquer chaque cellule visitée par la longueur du chemin le plus court la reliant au point de départ. On demande un algorithme de complexité linéaire.

Visualisez l’exploration avec la classe BreadthFirstWithDistance. La distance entre Marin et Nemo sera affichée automatiquement dans la console :

    Distance : 104

Testez votre code en utilisant Test22.java, puis déposez BreadthFirstWithDistance.java

2.3 Chemin le plus court

Complétez

1. la méthode traverse(...) de la classe BreadthFirstWithShortestPath, en adaptant celle de BreadthFirstWithDistance. La nouvelle méthode implémente toujours le même parcours en largeur, mais marque chaque cellule par la direction de retour (c’est-à-dire la direction opposée à celle par laquelle on est arrivé dans la cellule). Si Nemo est retrouvé, elle appelle backTrack(...) pour déterminer le chemin le chemin le plus court de Marin à Nemo.

2. la méthode backTrack(Ocean ocean, Coordinate current) de la classe BackTrackingTraversal. Celle-ci part de la cellule current et retrace le chemin parcouru en suivant les marques posées par la méthode précédente. Chaque cellule traversée durant ce rebroussement doit être marquée par path.

(Remarquez que la classe BreadthFirstWithShortestPath étend BackTrackingTraversal, qui, elle-même, étend Traversal. En conséquence, toutes les méthodes de ces deux dernières classes sont accessibles dans BreadthFirstWithShortestPath. Ainsi, on peut utiliser la méthode backTrack(...) dans BreadthFirstWithShortestPath.traverse(...).)

Visualisez l’exploration avec la classe BreadthFirstWithShortestPath.

Testez votre code en utilisant Test23.java.

Déposez BackTrackingTraversal.java.

Déposez BreadthFirstWithShortestPath.java.

3. Éviter les requins

Horreur ! Les requins sont arrivés.

Remplacez "no-sharks.txt" par "one-shark.txt" dans la méthode main(...) de la classe BreadthFirstWithShortestPath et exécutez à nouveau cette classe. Vous constaterez qu’elle calcule un chemin passant par ce requin, tandis que d’autres chemins certes plus longs l’évitent.

En adaptant le code de la question précédente, complétez la méthode traverse(...) de la classe AvoidSharks afin qu’elle calcule un chemin (pas forcément de longueur minimale) rencontrant un minimum de requins. Comme à la question précédente, la méthode traverse(...) doit poser des marques permettant de retracer le parcours et appeler backTrack(...) une fois Nemo trouvé pour marquer le meilleur chemin trouvé.

Visualisez l’exploration avec la classe AvoidSharks.

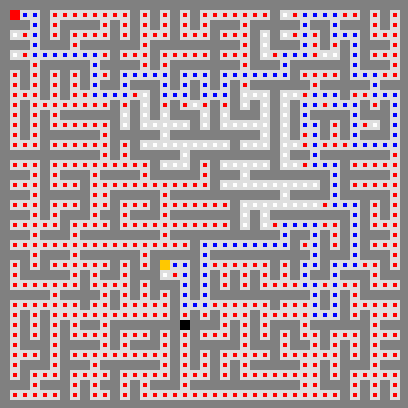
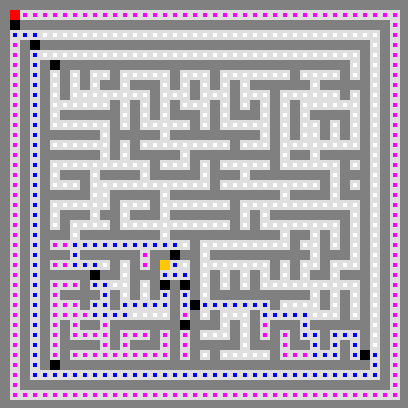
Vous pouvez maintenant tester votre code sur d’autres labyrinthes. La classe FindNemo lance tous les algorithmes de parcours à la suite sur la carte "many-sharks.txt". Vous pouvez changer la carte pour "no-sharks.txt" ou "one-shark.txt". Voici ci-dessous les comportements des divers parcours implémentés durant le TD sur cet océan.

Testez votre code en utilisant Test3.java, puis déposez AvoidSharks.java.

4. Question complémentaire

À force d’essayer d’éviter les requins, le pauvre Marin se fatigue beaucoup…

En effet, le chemin obtenu par la méthode de la question précédente n’est pas forcément le plus court parmi ceux qui rencontrent le moins de requins.

Une façon de comprendre ce qu’il se passe si l’on utilise une file à double entrée comme suggéré dans l’indication est d’observer que cette file à double entrée peut être vue comme la concaténation d’une pile et d’une file simple. Lors du parcours, on vide d’abord la pile, puis, lorsque celle-ci est vide, on retire un requin de la file et l’on recommence à l’utiliser comme une pile, et ainsi de suite. On obtient ainsi une sorte d’intermédiaire entre parcours en profondeur et parcours en largeur.

Comment remédier à ce défaut ? Plus précisément, comment modifier le parcours pour qu’il calcule un chemin de longueur optimale parmi ceux qui rencontrent le moins de requins? Saurez-vous le faire en maintenant la complexité linéaire ?

Complétez la méthode traverse(...) de la classe Bonus, puis lancez sa méthode main(...) :

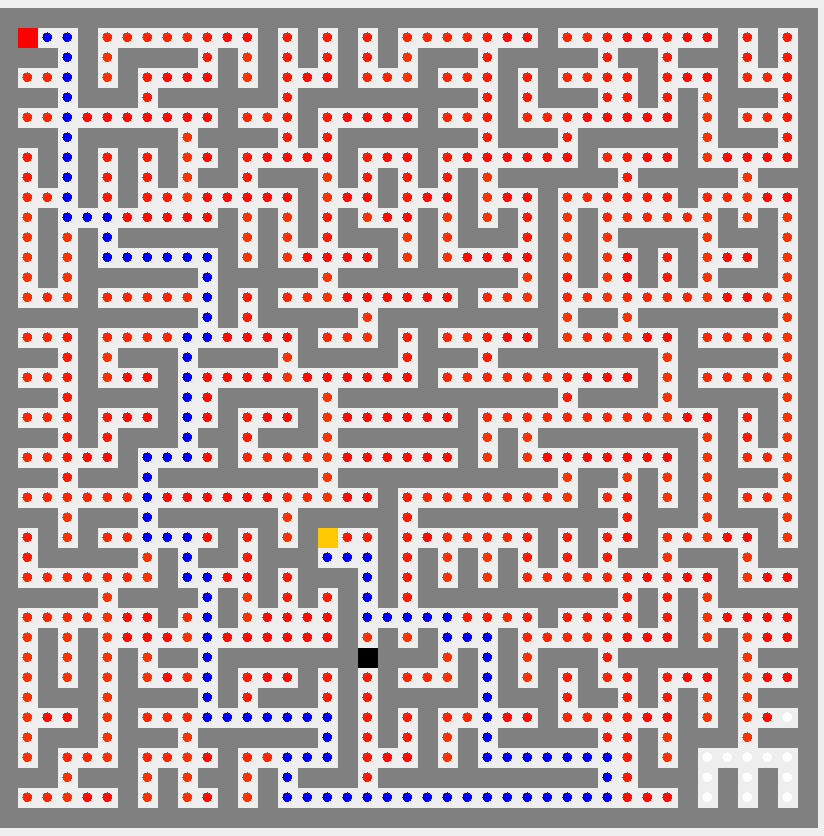
Testez votre code en utilisant la classe Test4.java, puis déposez Bonus.java.