Une OST basique
class Data implements Comparable<Data> {
final int key; // clé
final String value; // valeur associée à la clé
// Initialise la paire (key, valeur)
Data(int key, String value) {
this.key=key;
this.value=value;
}
// Effectue la comparaison entre la clé de la donnée courante et la clé associée à 'd'
@Override
public int compareTo(Data d) {
if(this.key<d.key) return -1;
else if(this.key>d.key) return 1;
return 0;
}
}
Le but de cet exercice est d’implémenter une version simple d’une Ordered Symbol Table (OST), munie des fonctions ci-dessous:
OSTNaive(int[] key, String[] value) |
initialise une OST représentant les paires (key[i], value[i]) |
boolean isEmpty() |
Teste si la table est vide |
int size() |
Renvoie le nombre de paires stockées |
void deleteMin(), deleteMax() |
Supprime la paire ayant la plus petite (resp. grande) clé. Ne fait rien si la table est vide |
String getMin(), getMax() |
Renvoie la valeur associée à la plus petite (resp. grande) clé. Renvoye null si la table est vide. |
String select(int r) |
Renvoie la valeur associée à la clé de rang r |
String get(int key) |
Renvoie la valeur associée à la clé key |
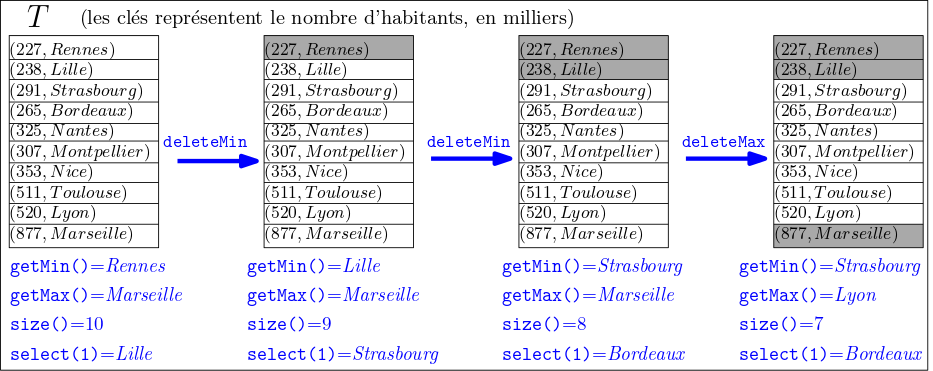
Les données manipulées sont des paires (int key, String value) où value est la valeur associée à la clé key. Elles sont codées par la classe Data (fournie, voir encadré sur la gauche). La comparaison entre deux données d1 et d2 peut se faire à l’aide de la méthode int compareTo(...).
Initialisation
On choisit une représentation simple, où les données (paires) sont stockées dans un tableau Data[] T. Certaines cases de T ne seront peut-être pas utilisées: vous pouvez ajouter à la classe OSTNaive deux champs min et max, pour indiquer que seules les cases dont les indices sont dans [min, max[ sont utilisées.
Dans la classe OSTNaive, ajouter les champs nécessaires et
compléter le constructeur OSTNaive(int[] key, String[] value)
compléter les méthodes size() et isEmpty(), deleteMin(), deleteMax().
Important : On supposera que key.length=value.length et que la clé key[i] est associée à la valeur value[i]. Mais il faudra prendre en compte que les tableaux key[] et value[] pris en entrée par le constructeur ne sont pas nécessairement triés.
Suggestion : pour trier un tableau Data[] T, vous pouvez vous servir de l’instruction Arrays.sort(T), déjà fournie par Java, qui trie les paires stockées dans T par rapport aux clés (en ordre croissant).
Tester votre code avec la classe Test11.
Déposer OSTNaive.java.
Sélection
Dans la classe OSTNaive, compléter les méthodes suivantes :
getMin(), getMax() qui renvoient la valeur associée à la clé de rang minimal (maximal). Ces fonctions renvoyent null si la table est vide.
String select(int r) qui renvoie la valeur associée à la clé de rang r (pour tout indice 0 ≤ r < n). La fonction doit renvoyer null si r < 0 ou r ≥ n.
Tester votre code avec la classe Test12.
Déposer OSTNaive.java.
Recherche
Il s’agit maintenant de munir la table d’une opération permettant de rechercher des paires à partir de leur clé.
Dans la classe OSTNaive, compléter la méthode suivante :
String get(int key) qui renvoie la valeur associée à key (le résultat renvoyé est null si la clé n’est pas trouvée).
Suggestion : vous avez le droit d’ajouter des méthodes auxilaires à la classe OSTNaive.
Remarque: Par souci d’efficacité, on essayera de proposer une solution de complexité O(log n) pour la fonction get(). La sélection doit pouvoir s’executer en temps O(1).
Tester votre code avec la classe Test13.
Déposer OSTNaive.java.
Arbres AVL et Dynamic OST
class DynamicOST {
private AVL t; // arbre représentant une "Dynamic Ordered Symbol Table"
// Construit une table vide
DynamicOST() { this.t=null; }
// Teste si l'arbre 't' est bien un arbre de recherche AVL
boolean checkCorrectness() { return AVL.isAVL(t); }
// Teste si la table est vide
boolean isEmpty() { return t==null; }
// Renvoie le nombre d'éléments stoqués dans la table
int size() { return AVL.size(this.t); }
// Renvoie la valeur associée à une clé donnée.
// Renvoie 'null' si la structure de données ne contient pas la clé 'key'. */
String get(int key) { return AVL.get(t, key); }
...
}
Dans cet exercice, nous souhaitons implémenter une Ordered Symbol Table avec des fonctionnalités un peu plus riches : le but est d’obtenir une Dynamic Ordered Symbol Table (DOST) qui soit munie d’opérations de mises à jour (insertion et suppression d’une clé arbitraire et valeur associée) et ensemblistes (union de deux ensembles).
Pour cela, nous allons utiliser la classe DynamicOST (à compléter), qui maintient dans un champ private AVL t l’ensemble des paires de la table sous la forme d’un arbre AVL t (amphi 5). Les nœuds sont représentés à l’aide de la classe AVL (implémentation fournie, voir encadré sur la gauche).
class AVL {
int key; // clé stoquée dans chaque noeud
String value; // valeur stoquée dans chaque noeud
AVL left, right; // fils gauche et droit
int height, size; // hauteur et nombre de noeuds de l'arbre
// Construit un noeud contenant la paire (key, value)
AVL(int key, String value) {
this.left = this.right = null;
this.key = key;
this.value=value;
this.height = 1;
this.size=1;
}
// Construit un noeud contenant (key, value), et ayant 'left' et 'right'
// comme sous-arbres gauche et droit
AVL(AVL left, int key, String value, AVL right) {
...
this.height = 1 + Math.max(height(left), height(right));
this.size = 1 + size(left) + size(right);
}
// affiche les noeuds de l'arbre
static void print(AVL node) {...}
...
}
Un nœud contient un champ String value (la donnée stockée dans le nœud) et un champ int key (la clé) ainsi que les références des sous-arbres gauche et droit. De plus, chaque nœud stocke aussi la taille et la hauteur du sous-arbre dont il est racine. L’arbre vide est représenté par null.
Suggestion (aide pour débogage) : La classe AVL est munie d’une méthode void print(AVL node) qui affiche les nœuds de l’arbre par niveaux. L’arbre illustré dans l’exemple sera ainsi affiché :
(291,Strasbourg)
(238,Lille) (511,Toulouse)
(227,Rennes) (265,Bordeaux) (325,Nantes) (520,Lyon)
(307,Montpellier) (353,Nice) (877,Marseille)
En plus des opérateurs déjà définis à la Section 1, on souhaite implémenter les méthodes suivantes :
void insert(int key, String value) |
ajoute dans la table la paire (key, value). On pourra supposer que la table ne contient pas déjà la nouvelle paire (key, value) à insérer. |
void delete(int key) |
supprime la paire (key, value) si une telle paire existe. Ne fait rien autrement. |
void union(DynamicOST T) |
qui ajoute aux éléments du tableau courant ceux de T |
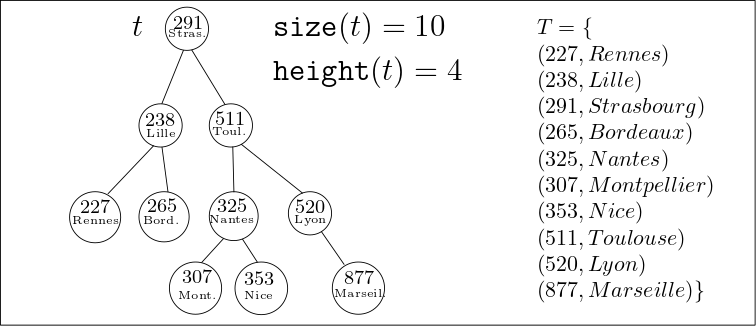
L’image ci-dessous illustre un arbre AVL représentant 10 villes de France, où la clé représente leur population (en milliers).
Split et Join sur des arbres AVL
La classe AVL fournie contient une implémentation efficace d’opérations appelées split() et join(). Ces opérations maintiennent la propriété d’équilibrage des arbres AVL, et vont permettre de programmer facilement les opérations de mise à jour de notre table (e.g. suppression, insertion, union, intersection…). Les opérations split() et join() ont les spécifications suivantes :
Illustration des méthodes join(...) et split(...) 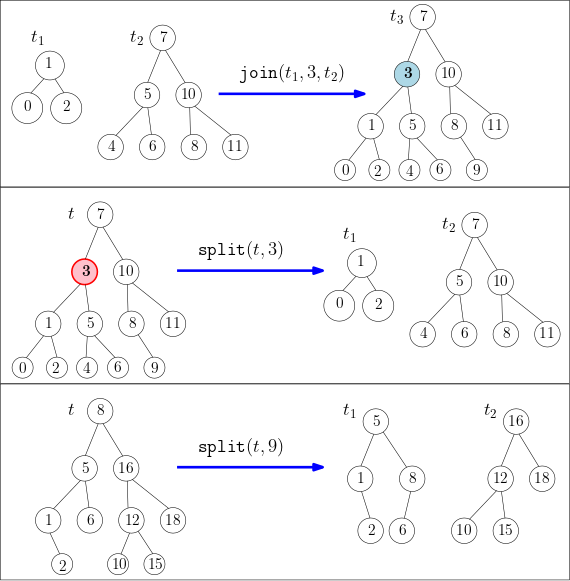
AVL join(AVL t1, int k, String v, AVL t2) |
Étant donnés deux arbres AVL t1 et t2, ainsi qu’une clé k, renvoie un nouvel arbre AVL t3 contenant tous les éléments de t1, la paire (k, v) et ceux de t2 (en supposant que tous les éléments de t1 sont inférieurs à k et que k est inférieur à tous les éléments de t2). |
AVL join(AVL t1, AVL t2) |
Étant donnés deux arbres AVL t1 et t2, renvoie un nouvel arbre AVL t3 contenant tous les éléments de t1 et t2 (en supposant que tous les éléments de t1 sont plus petits que ceux de t2). |
AVL[] split(AVL t, int key) |
Étant donné un arbre t, et une clé key (qui appartient ou non à l’arbre), renvoie un tableau de taille 2 stockant un couple d’arbres AVL obtenue après la subdivision de l’arbre t autour de la clé key : le premier contient les éléments plus petits que key et le second les éléments plus grands (si la clé key appartient à t, elle est supprimée). |
Ajout et suppression
On souhaite munir notre table des fonctionnalités d’ajout et suppression.
Dans la classe DynamicOST, compléter
la méthode void insert(int key, String value) qui ajoute la paire (key, value)
la méthode void delete(int key) qui supprime l’élément ayant key comme clé (la fonction ne fait rien si un tel élément n’existe pas).
Indication : Les opérations peuvent s’implémenter de manière simple et efficace à l’aide des fonctions join(...) et split(...) fournies par la classe AVL et illustrées plus haut.
Tester votre code avec la classe Test21.
Déposer DynamicOST.java.
Sélection de la valeur avec clé de rang r
Dans la classe DynamicOST, compléter la méthode String select(int r) qui renvoie la valeur associée à la clé de rang r (pour tout indice 0 ≤ r < n). La fonction doit renvoyer null si r < 0 ou r ≥ n.
Suggestion : Vous avez le droit d’ajouter des méthodes auxiliaires à la classe DynamicOST.
Tester votre code avec la classe Test22.
Déposer DynamicOST.java.
Opérations ensemblistes sur un DOST
Dans la classe DynamicOST, compléter la méthode void union(DynamicOST table) qui ajoute aux éléments contenus dans la table courant ceux contenus dans table. On pourra supposer que les éléments stockés dans les deux tables sont distincts.
Remarque: il pourra s’avérer utile de se servir d’une fonction auxiliaire static AVL unionRec(AVL t1, AVL t2) qui renvoie un arbre AVL représentant l’union des deux tables représentées par t1 et t2.
Suggestion : L’union de deux arbres AVL peut se coder assez facilement de manière récursive à l’aide des fonctions split(...) et join(...) qui sont fournies par la classe AVL.
Tester votre code avec la classe Test23.
Déposer DynamicOST.java.


