| Votre opinion sur le cours de lundi : | Votre opinion sur le TD de la semaine dernière : | |
TD4 pour le TD de cette semaine.src.zip et enregistrez les fichiers .java dans le dossier src du projet TD4. Enregistrez les fichiers .txt directement dans le projet TD4.Le TD adopte le plan suivant :
Le code que vous venez de télécharger est organisé en plusieurs classes. Voici leurs fonctionnalités principales :
La classe Maze modélise un labyrinthe. Elle contient le tableau grid de Cell à 2 dimensions. La taille du tableau est heightxwidth.
getCell permet d’acceder à la case avec les coordonnées (i, j).getFirstCell() renvoie la première case, c’est-à-dire la case avec les coordonnées (0, 0).La classe Cell modélise une case d’un labyrinthe. Chaque case a donc quatre cases voisines possibles : au nord, à l’est, au sud et à l’ouest. Un mur peut bloquer le passage vers chacune de ces cases voisines.
getNeighbors(boolean ignoreWalls) renvoie une liste des cases voisines. Si l’argument ignoreWalls est true, alors toutes les cases voisines sont renvoyées. Si l’argument ignoreWalls est false, alors seules sont renvoyées les cases vers lesquelles un passage existe.breakWall(Cell c) permet de créer un passage de la case actuelle vers la case c donnée en argument. Elle supprime donc un mur.setMarked. L’existence d’une marque peut être testée avec la méthode isMarked.Dans cette première question, nous voulons trouver un chemin dans un labyrinthe donné, allant du coin nord-ouest au coin sud-est, c’est-à-dire de la case avec les coordonnées (0, 0) à la sortie, dans notre cas celle avec les coordonnées (height-1, width-1). La méthode isExit de la classe Cell peut être utile : elle renvoie true si et seulement si la case actuelle est la sortie. Le chemin doit être signalé avec des marques sur les cases. Plus précisément, un appel à la méthode isMarked doit renvoyer true pour toutes les cases sur le chemin et false pour toutes les cases qui ne sont pas sur le chemin.
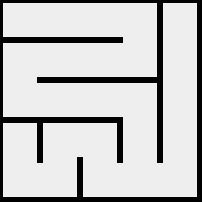
Par exemple, dans le labyrinthe 5x5

le chemin unique du nord-ouest au sud-est est
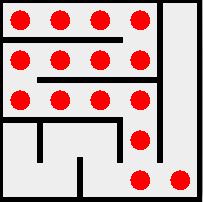
où une case marquée se distingue par un cercle rouge.
Compléter la méthode searchPath() de la classe ExtendedCell, de sorte que : (1) elle renvoie true s'il existe entre this et la case sortie un chemin ne passant par aucune case marquée ; (2) elle renvoie false sinon, et dans ce cas, elle ne modifie aucune marque.
Pour trouver un chemin de l’entrée à la sortie dans le labyrinthe, il suffira d’appeler la méthode sur l’instance de Cell représentant la case (0,0). C’est ce qui est fait dans les tests.
Vous remarquez sans doute que la méthode commence avec l’appel maze.slow(). C’est utilisé pour ralentir l’animation de la recherche de chemin pour qu’elle soit observable à l’œil nu.
Testez avec le fichier Test1.java.
Dans le reste du TD, nous allons travailler sur la génération de labyrinthe. Comme pour les labyrinthes de la question 1, ils doivent être parfaits, c’est-à-dire avoir la propriété qu’il y ait un chemin unique entre chaque paire de cases. Initialement, toutes les cases sont isolées (i.e. il y a des murs dans toutes les quatre directions).
Le rebroussement récursif pour la génération a la même structure générale que la recherche de chemin. Une différence est qu’il n’est pas nécessaire de marquer des cases. Une autre différence est la condition pour l’appel récursif : nous voulons continuer seulement si le voisin est isolé. Sinon, cela conduirait à créer un cycle et le labyrinthe ne serait pas parfait.
Pour ne pas toujours aboutir au même labyrinthe, nous voulons parcourir les directions dans un ordre aléatoire. Pour faire cela on peut utiliser la méthode statique shuffle de la classe auxiliaire Collections qui prend une liste et la permute aléatoirement.
Nous avons donc la structure suivante simple pour notre algorithme dans la méthode generateRec de la classe ExtendedCell:
breakWall) et faire un appel récursif avec le voisin.Testez votre méthode avec le fichier Test2.java.
Nous allons maintenant traduire l’algorithme de génération récursif en une version itérative. Cela veut dire que nous échangeons la pile d’appels contre une liste chaînée qui contient les coordonnées des cases dont nous avons commencé le traitement.
Une approche itérative peut avoir plusieurs avantages : moins d’espace sur la pile d’appels et plus de contrôle sur l’ordre dans lequel les cases sont visitées. La pile d’appels choisit toujours l’élement le plus récent. Avec une liste explicite on peut changer ce comportement.
La classe Bag (implémentée dans le fichier Util.java, que vous n’avez pas besoin de regarder) offre plusieurs manières de choisir le prochain élément (de type Cell) d’une liste. Les quatre différentes manières disponibles sont: NEWEST (on choisit l'élément le plus récent), OLDEST (pour l'élément plus ancien), MIDDLE (l'element au milieu de la liste) et RANDOM (un element aleatoire de la liste). Pour chacune des quatre options, la méthode peek() renvoie l’élément sélectionné selon le choix. La méthode pop() supprime cet élément. Les deux méthodes supposent une liste non-vide. Pour tester si la liste est effectivement vide, on peut utiliser la méthode isEmpty(). La méthode add(Cell c) permet de rajouter un nouvel élément c à la fin de la liste. On précise également que les méthodes peek() et pop() sont synchronisées. En particulier, si une cellule est sélectionnée dans la liste avec peek() et que d’autres cellules sont ajoutées à la liste, l’appel à pop() supprime la cellule sélectionnée.
Pour implémenter l’algorithme itératif dans la méthode generateIter de la classe Maze, on peut suivre le processus suivant. L’algorithme commence avec une liste qui ne contient que l’élément (0, 0), puis rentre dans une boucle, comme ceci :
Vous pouvez remarquer qu’un choix de NEWEST revient à la version récursive. Un choix de RANDOM produit des labyrinthes tout à fait intéressants aussi, ce qui n’est pas le cas pour les choix MIDDLE ou OLDEST.
Testez votre méthode avec le fichier Test3.java.
Nous venons d’implémenter des algorithmes de génération de labyrinthes aléatoires. La forme des labyrinthes générés par le rebroussement itératif dépendait fortement du choix de la méthode de sélection de la prochaine case à traiter. En particulier, les labyrinthes générés ne sont pas uniformement distribués dans l’ensemble de tous les labyrinthes parfaits de la taille donnée.
Dans cet exercice nous allons donc implémenter un algorithme de génération uniforme. La méthode de génération choisie s’appelle l’algorithme de Wilson. Il procède comme suit :
Choisir une case uniformement au hasard et la marquer.
Tant qu’il y a une case non-marquée, choisir une case non-marquée uniformement au hasard, et
breakWall) le long de la marche générée.Voici l’algorithme en plein milieu d’exécution :

Implémenter l’algorithme de Wilson en complétant la méthode generateWilson() de la classe Maze.
Pour tirer des cases uniformes aléatoires successivement, il suffit de mettre toutes les cases dans un tableau et de le mélanger. On pourra ajouter à la classe Cell un champ Cell next, pour garder trace de la direction prise par la marche aléatoire la dernière fois qu’elle quitte une case.
Testez votre méthode avec le fichier Test4.java.