
L’archive src.zip est à
décompresser dans le répertoire TD10 (le répertoire racine
de votre projet) et contient :
Dijkstra et
BiDijkstra à compléter au fur et à mesure du TD,Graph, Node, Edge
(pour la modélisation des graphes) et les classes Fenetre,
ColoredPoint2D, ColoredSegment2D (pour la
visualisation), que vous ne devez pas modifier,Test, Test0,
Test11, …, Test4, utilisées pour tester votre
code.Le fichier data.zip est
également à décompresser dans le répertoire TD10. Il
contient les données combinatoires et géographiques de deux réseaux
routiers.
Ainsi, vous devez vous retrouver avec l’arborescence suivante :
TD10
|
|--> src
| |
| |--> ColoredPoint2D.java
| |--> ColoredSegment2D.java
| |--> Edge.java
| |--> Fenetre.java
| |--> Graph.java
| |--> Node.java
| |--> TD10.java
| |--> Test.java
| |--> Test0.java
| \ ...
|
\--> data
|
|--> NY_Metropolitan.png
|--> USA-road-d-NY.co
|--> USA-road-d-NY.gr
\--> mini.grTestez les classes fournies avec le fichier
Test0.java.
Vous devez voir s’afficher :
Test 0 : test de la classe Graph
Loading road networks from file mini.gr ... done
Loading road networks from file USA-road-d-NY.gr ... done
Loading geometric coordinates from file USA-road-d-NY.co ... done
Loading background image from file NY_Metropolitan.jpg ... doneet la carte :

Remarque : Si vous faites ce TD ailleurs qu’en salle machine, il
est possible que vous obteniez une erreur du type
Exception in thread "main" java.lang.OutOfMemoryError: Java heap space.
Cela est dû au fait que les graphes que nous vous faisons manipuler,
comportant beaucoup de sommets (environ 250 000), épuisent toute la
mémoire.
Dans ce cas, reportez-vous à la rubique «Activer assert's et augmenter l'espace mémoire alloué à la machine virtuelle».
Nous allons aujourd’hui nous intéresser au problème du calcul d’un plus court chemin dans un graphe. C’est un problème qui se pose par exemple dans les logiciels de GPS qui doivent calculer des itinéraires routiers. Lorsque les graphes sont gros, il faut utiliser des algorithmes performants pour calculer des plus courts chemins en un temps acceptable par l’utilisateur : c’est bien le cas des réseaux routiers, qui correspondent à des graphes avec plusieurs centaines de milliers (voir millions) de sommets.

Nous allons implémenter l’algorithme de Dijsktra. Cet algorithme s’applique à des graphes dont les poids des arêtes sont positifs ou nuls. Nous implémenterons ensuite un algorithme de recherche bidirectionnelle basé sur Dijkstra. Les animations ci-dessous illustrent les deux algorithmes que vous allez coder aujourd’hui.

GraphNous allons travailler sur des graphes orientés où les poids des arcs
sont des entiers strictement positifs. Par convention, les sommets
seront les entiers 0, 1, ..., n-1. On vous fournit la
classe Graph dont les champs et méthodes publiques sont les
suivants :
nbVertices indique le nombre de sommets
du graphe,nbEdges indique le nombre d’arcs du
graphe,Graph(String file) construit un graphe
à partir du fichier file,ArrayList<Integer> successors(int i)
renvoie la liste des successeurs du sommet i,int weight(int i, int j) renvoie le poids de
l’arc (i,j) si ce dernier existe, et
Integer.MAX_VALUE sinon,Graph reverse() renvoie un nouveau graphe où
les orientations des arcs ont été inversées, et les poids
inchangés.Il n’est pas utile de lire le code de la classe Graph.
La description ci-dessus est suffisante pour l’utiliser dans ce TD.
Notre problème consiste à calculer la longueur d’un plus court chemin
entre un sommet source et un sommet destination dans un graphe orienté.
Pour ce faire, nous allons coder l’algorithme de Dijkstra. La classe
Dijkstra fournie contient les champs suivants :
final Graph g contenant le graphe,final int source contenant la source du plus
court chemin recherché,final int dest contenant la destination du
plus court chemin recherché,Fenetre f nécessaire pour l’affichage
graphique. Vous n’aurez pas à vous soucier de l’initialisation de ce
champ.Le squelette contient un constructeur standard
Dijkstra(Graph g, int source, int dest).
Attention : Tout sommet du graphe peut servir de
source ou de dest. En particulier, aucun de
ces deux sommets n’est forcément le sommet 0.
Rappelons comment fonctionne l’algorithme de Dijkstra. Cet algorithme fait intervenir la manipulation des informations suivantes
W (working
set) qui contient l’ensemble des sommets (rencontrés) qu’il reste
à examiner,dist qui indique, pour chaque
sommet i, la distance minimale trouvée entre i
et la source.L’algorithme procède comme suit.
Au départ :
0, tous les
autres sommets sont considérés comme étant à une distance infinie,
puisqu’on n’a pas encore trouvé de chemins. En pratique, un entier
suffisamment grand fera l’affaire, par exemple
Integer.MAX_VALUE.W contient uniquement la source.Tant qu’il reste des sommets à examiner (i.e. W
n’est pas vide) :
W le sommet x, avec la plus
petite valeur dist[x]x est la destination, on renvoie
dist[x],x n’est pas la destination — on
recalcule les distances de la source à tous les successeurs de
x :y successeur de x tel quedist[y] > dist[x] + g.weight(x,y)on pose
dist[y] = dist[x] + g.weight(x,y)et on rajoute y dans W (il se peut que
y soit déjà dans W — on verra cela en détail
plus tard).
À la fin :
W est vide alors qu’on n’a pas encore rencontré la
destination et l’algorithme renvoie alors -1, puisqu’aucun
chemin n’existe entre la source et la destination (ceci ne devrait pas
nous arriver aujourd’hui).Cet algorithme fait intervenir
dist,W,W du sommet x, avec la plus
petite valeur dist[x].Dans la suite, nous allons progressivement introduire ces trois éléments.
Tout d’abord, ajoutez un champ int[] dist à la
classe Dijkstra et mettez à jour le constructeur
Dijkstra() afin d’initialiser ce champ
correctement.
Nous allons ajouter les informations suivantes que nous maintiendrons durant le déroulement de l’algorithme :
un tableau d’entiers pred à nbVertices
cases, où pred[i] indiquera le prédécesseur du sommet
i dans le plus court chemin obtenu entre
source et i, ou -1 si aucun
chemin n’a encore été trouvé jusqu’au sommet i,
un tableau de booléens settled à
nbVertices cases, où settled[i] sera vrai si
on a déterminé la plus courte distance au sommet i, et faux
si ce sommet est encore susceptible de changer de distance à la
source.
Par ailleurs, nous dirons qu’un sommet a été atteint lorsqu’au moins
un chemin a été trouvé entre la source et ce sommet. Cela revient à dire
qu’un sommet a été atteint lorsque son prédécesseur est différent de
-1. Pour la source, nous conviendrons qu’initialement elle
est son propre prédécesseur et qu’elle n’est pas encore traitée.
Ajoutez ces champs à la classe Dijkstra et
modifiez le constructeur de sorte que ces champs soient correctement
initialisés.
Afin de vérifier votre classe Dijkstra, exécutez
le fichier Test11.java. Vous devez
obtenir :
Test 1.1 : Initialisation de la classe Dijkstra
Loading road networks from file mini.gr ... done
Test de source... [OK]
Test de dest... [OK]
Test de dist, pred et settled... [OK]Déposez le fichier Dijkstra.java
WDans la description de l’algorithme de Dijkstra apparaît un ensemble
noté W qui correspond aux sommets atteints mais pas encore
traités. Sur cet ensemble, nous voulons pouvoir faire les opérations
suivantes
Pour être efficace, nous savons que nous pouvons assurer ces deux opérations en temps logarithmique en le nombre de sommets contenus dans cet ensemble, à condition d’utiliser une structure appropriée. En l’occurrence, nous allons utiliser ici une file de priorité, qui permet l’ajout d’un élément et le retrait du minimum en temps logarithmique. La priorité d’un élément sera définie par sa distance à la source.
Il y a toutefois une subtilité. Les priorités des sommets peuvent
être amenées à changer, par exemple si un sommet déjà atteint est de
nouveau atteint via un chemin plus court. Dans un tel cas, il faut
pouvoir modifier la priorité de cet élément dans la file de priorité, ce
qui est assez complexe. Nous allons habilement contourner ce problème en
faisant la chose suivante : lorsque la priorité d’un sommet
i contenu dans l’ensemble W doit être
modifiée, nous insérerons dans W une nouvelle occurrence de
i avec la nouvelle priorité. Nous savons que cette nouvelle
occurrence de i sortira de W avant l’ancienne,
puisque les éléments sortent par ordre croissant. En contrepartie, il se
pourra qu’un sommet sorti de W soit déjà définitivement
traité par l’algorithme et il faudra donc le vérifier.
Nous allons donc utiliser une file de priorité qui contiendra des
éléments de type Node, composé d’un identifiant
id (le numéro du sommet) et d’une valeur val
(sa priorité, c’est-à-dire sa distance à la source). Pour créer un
sommet correspondant au sommet id, nous utiliserons le
constructeur Node(int id, int val).
Ajoutez un champ
PriorityQueue<Node> unsettled à la classe
Dijkstra. Ce dernier représentera l’ensemble
W dans la description de l’algorithme. Modifiez le
constructeur de la classe pour initialiser correctement
unsettled et y insérer la source.
Les méthodes dont nous aurons besoin sur les files de priorités seront :
boolean isEmpty() qui renvoie true si et
seulement si la file est vide,void add(Node n) qui ajoute n,Node poll() qui renvoie l’élément dont la distance à la
source est minimale et l’enlève de la file.Testez avec le fichier Test12.java. Vous devez
obtenir :
Test 1.2 : Initialisation de la classe Dijkstra
Loading road networks from file data/mini.gr... done
Test de unsettled (ensemble W)... [OK]Déposez le fichier Dijkstra.java
Nous avons désormais tout ce qu’il faut pour coder une version efficace de l’algorithme de Dijkstra. Rappellons encore une fois que le calcul effectué par cet algorithme procède ainsi :
Tant qu'il y a des sommets à traiter
On pioche un sommet dans le working set W
On met à jour ce sommet, ses successeurs et WOn va l’implémenter progressivement, de manière bottom-up,
c’est-à-dire, en partant des petites fonctionnalités pour assembler le
tout. (Cette manière de procéder nous permettra plus tard, dans
l’exercice 3, de réutiliser la méthode oneStep(), qui
calcule un pas de la boucle, séparément du reste.)
Complétez la méthode
void update(int succ, int current) qui effectue
les mises à jour sur le successeur succ du sommet
current pioché dans W dans le corps de la
boucle. En particulier, dans le cas où une mise à jour est effectuée sur
dist[succ], on mettra à jour le prédécesseur du sommet
succ, et on insérera le sommet succ avec sa
nouvelle priorité dans la file unsettled.
Complétez la méthode int nextNode() qui
effectue le choix dans W du sommet current,
avec la plus petite valeur dist[current]. Il s’agit de
retirer de unsettled des sommets dans l’ordre de leur
priorité, jusqu’à rencontrer un sommet non encore traité et le renvoyer.
Renvoyer -1 si la file de priorité est vide ou si tous les
sommets restant dans la file ont déjà été traités.
Complétez la méthode int oneStep() qui
réalise une itération de la boucle principale de l’algorithme de
Dijkstra : extraire de W le prochain sommet
current à traiter, renvoyer -1 s’il ne reste
aucun sommet à traiter, marquer current comme traité,
mettre à jour tous les successeurs de current, renvoyer le
sommet current qui vient d’être traité.
Enfin, complétez la méthode
int compute() qui calcule et renvoie la longueur
d’un plus court chemin. Elle fonctionne de la manière suivante : tant
qu’on n’a pas traité la destination et qu’il reste au moins un sommet à
traiter, on réalise une itération. Ensuite, on renvoie -1
ou la valeur du plus court chemin suivant que la destination a été
atteinte ou non.
Testez vos méthodes avec la classe Test2 dans le
fichier Test2.java.
Vous devez obtenir :
Test 2 : test de l'algorithme de Dijkstra unidirectionnel utilisant le graphe dans 'mini.gr'...
*** ATTENTION : dans l'affichage, la numérotation des nœeuds commence à 0 ***
*** (et non à 1 comme dans 'mini.gr') ***
Loading road networks from file data/mini.gr... done
Test de la methode update()... [OK]
Test de la methode nextNode... [OK]
Test de la methode oneStep... [OK]
Test de la methode compute... [OK]Maintenant, pour visualiser le résultat, il faut :
slow()
au tout début de la fonction oneStep() (pour ralentir la
visualisation),g.drawUnsettledPoint(f, succ); juste après avoir
ajouté le point succ à l’ensemble
unsettled,g.drawSettledPoint(f, current); juste après avoir
fixé la valeur de settled[current] à
true,Exécutez la classe Test2bis dans le fichier Test2bis.java. Vous
devez voir avancer votre ensemble de points traités (en rouge) et les
points de W (en vert).
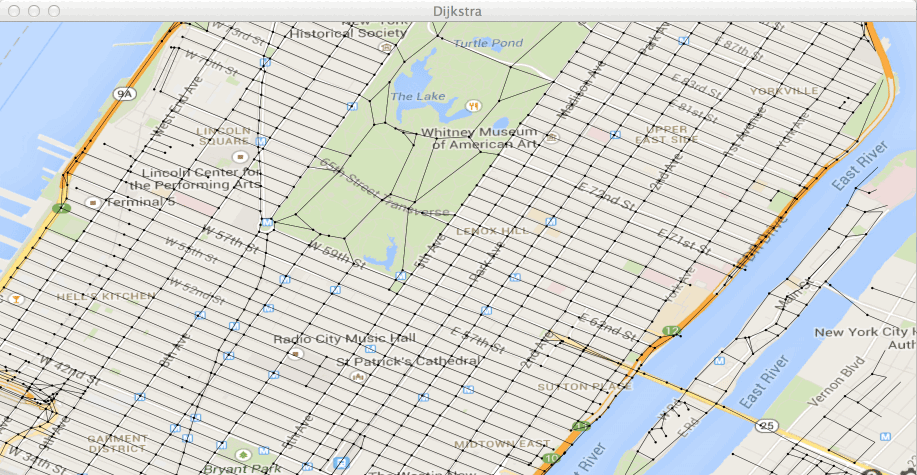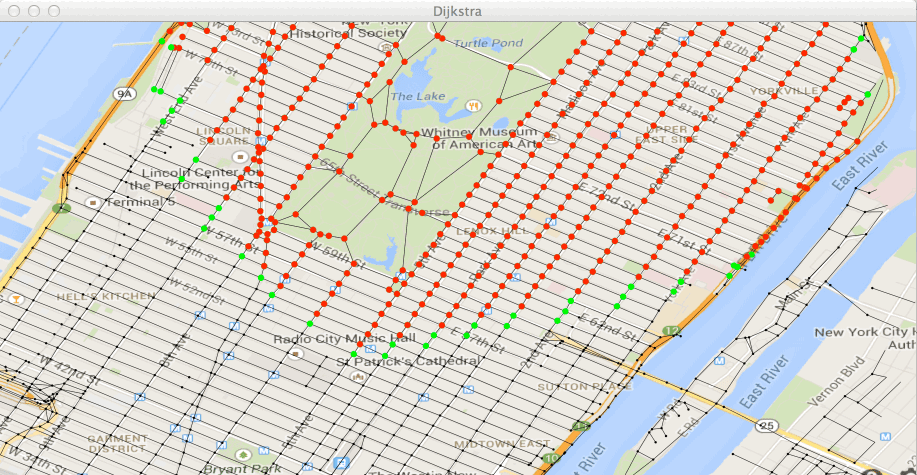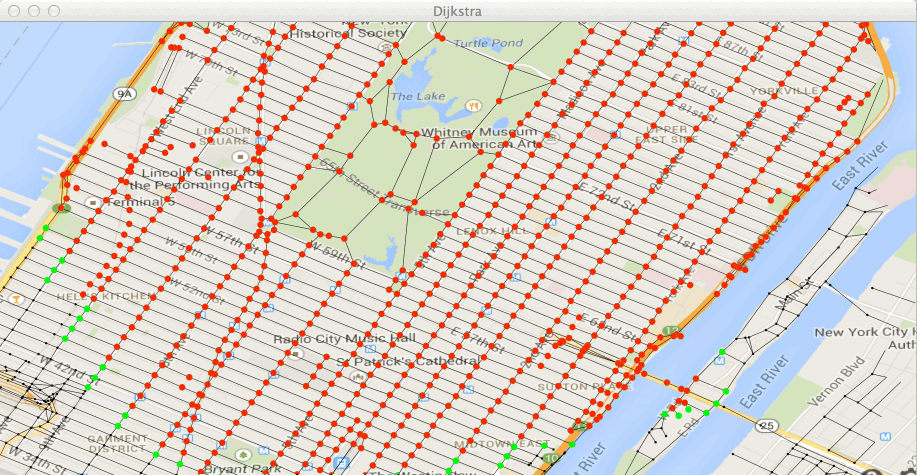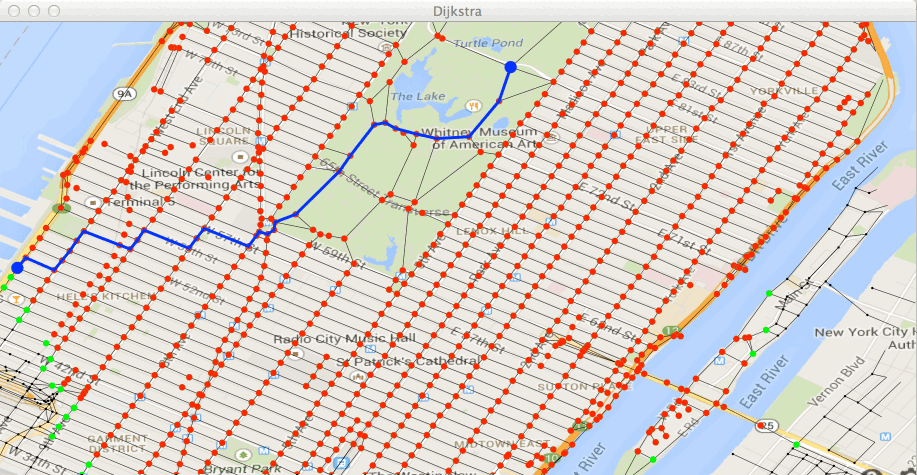
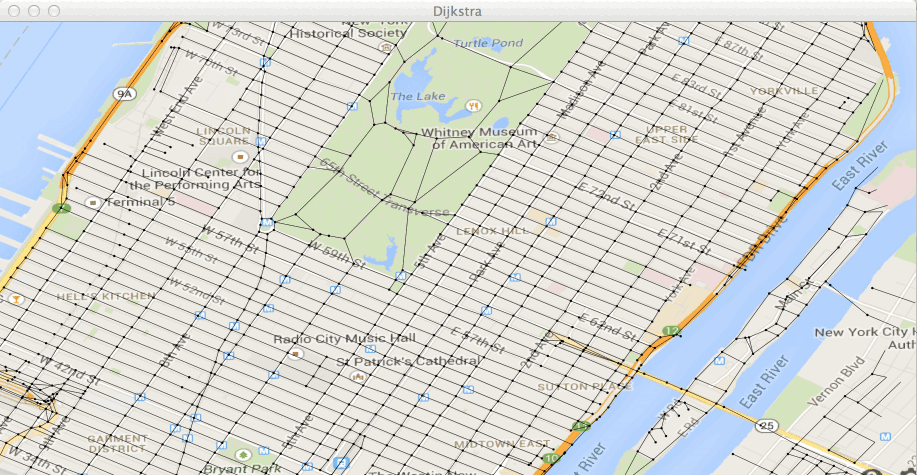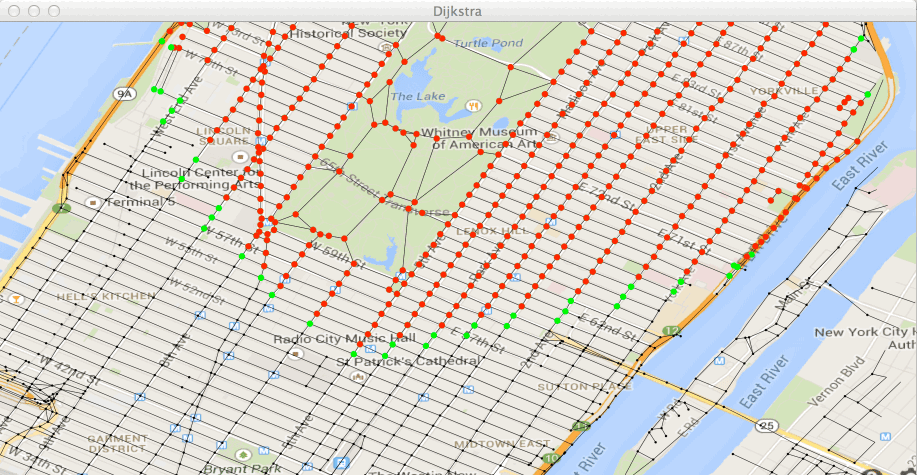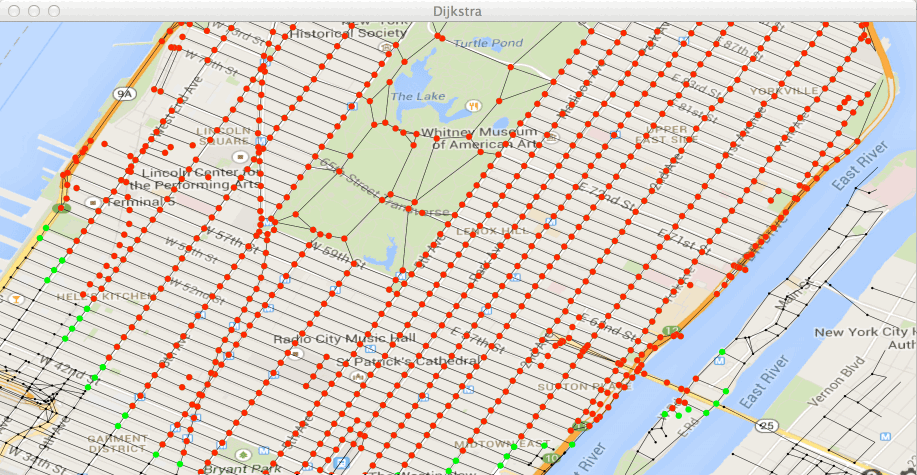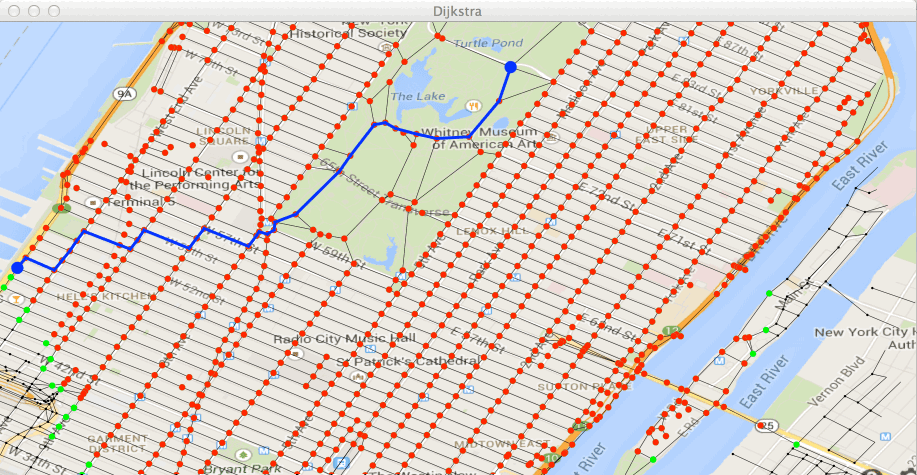
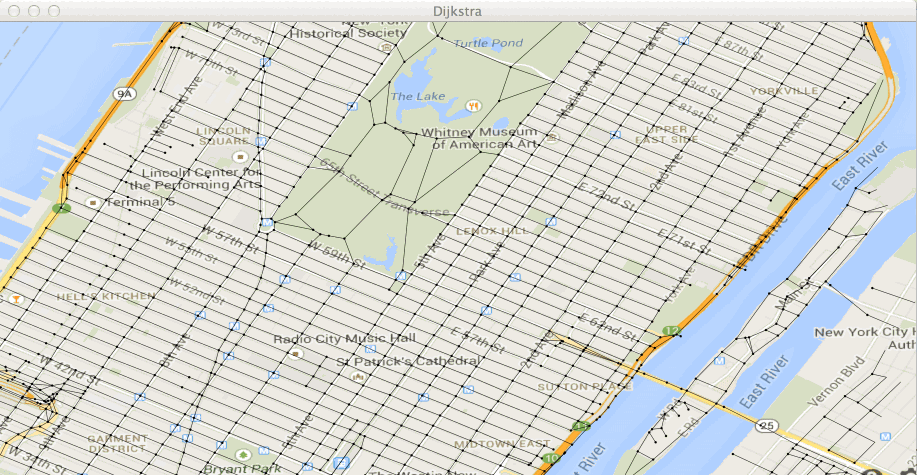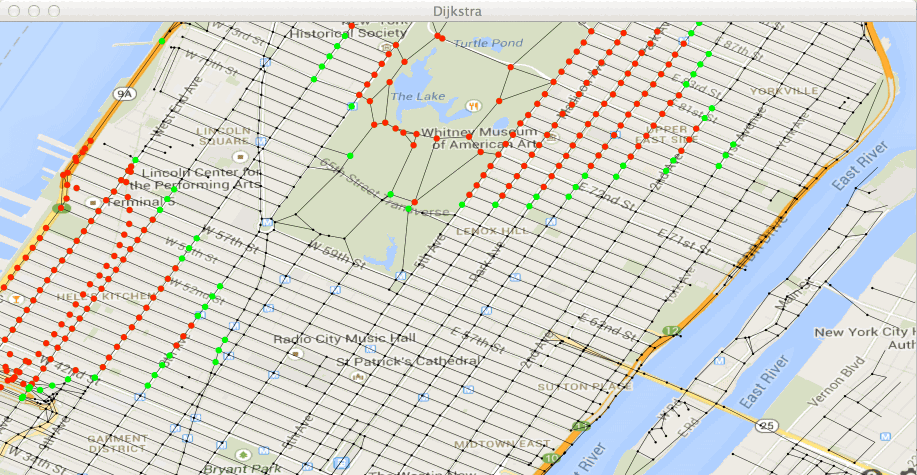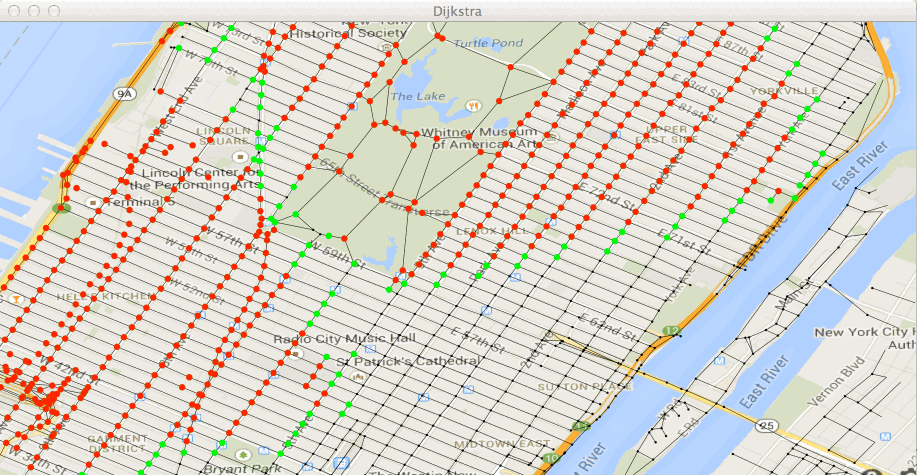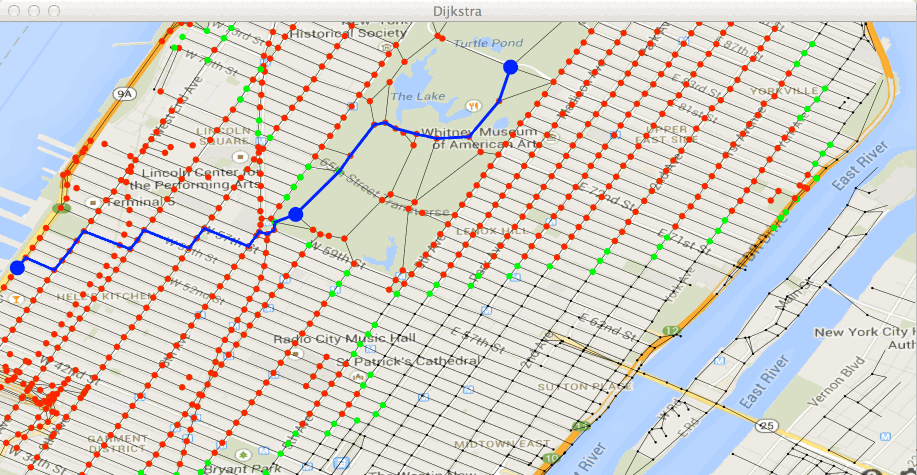
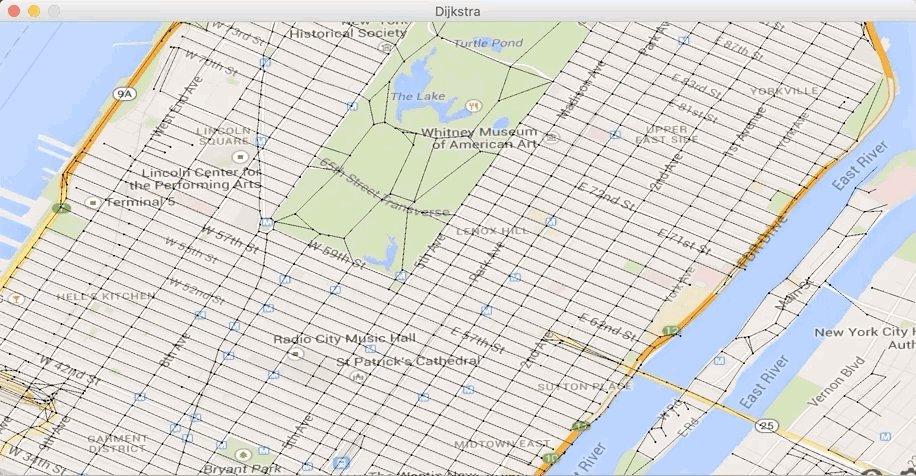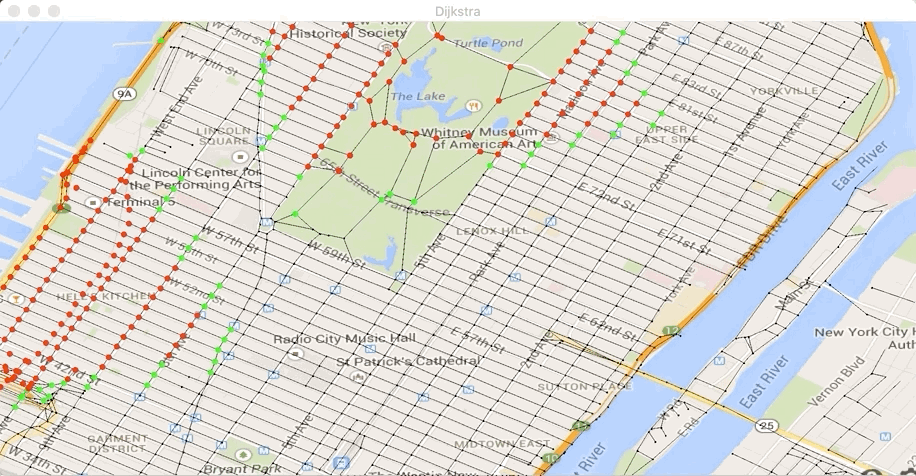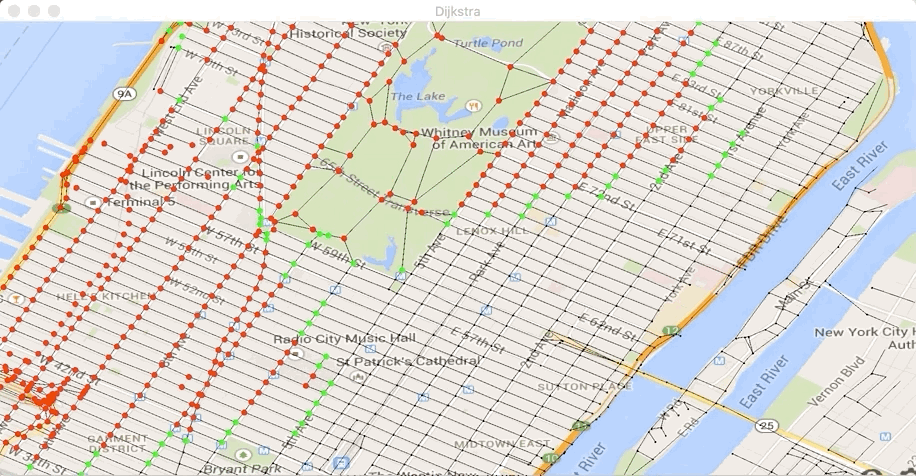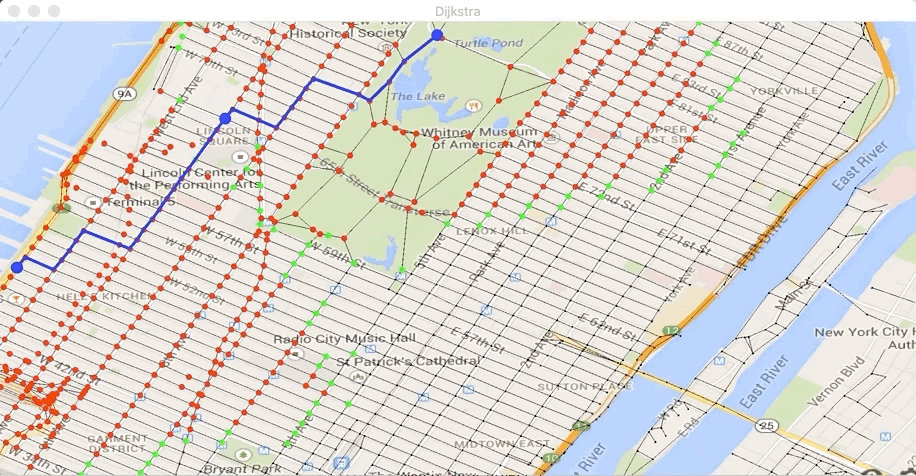
À la fin, vous devez obtenir le plus court chemin suivant :
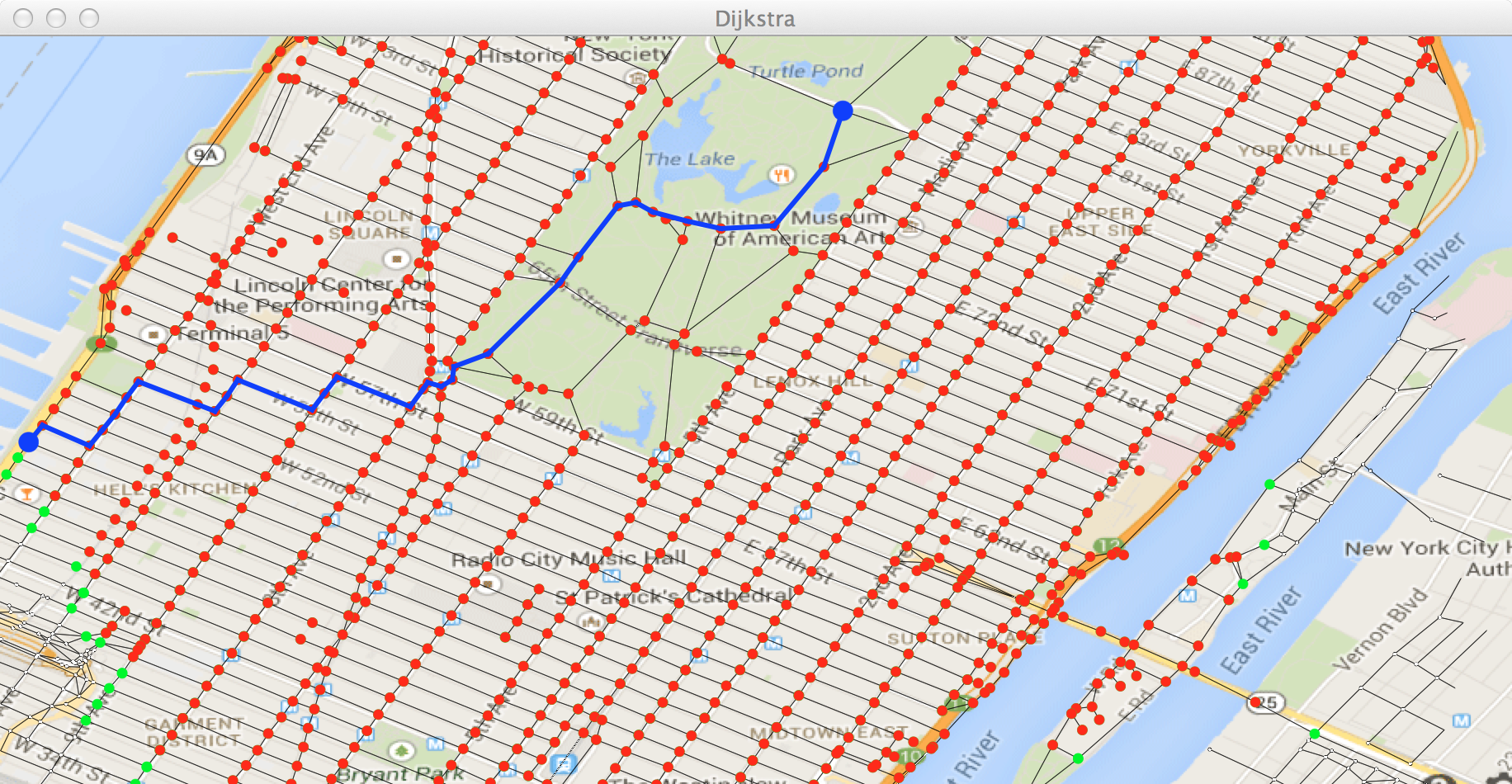
et vous devez voir s’afficher :
Test de l'algorithme de Dijkstra unidirectionel sur un gros graphe
Loading road networks from file data/USA-road-d-NY.gr... done
Loading geometric coordinates from file data/USA-road-d-NY.co ... done
Loading background image from file data/NY_Metropolitan.png ... done
plus court chemin entre 190637 et 187333 = 39113Déposez le fichier Dijkstra.java
À partir de maintenant, on suppose qu’il existe toujours au moins un chemin entre la source et la destination.
Nous allons désormais utiliser l’algorithme de Dijkstra pour faire une recherche bidirectionnelle, qui sera typiquement plus rapide sur des graphes issus de cartes comme ici.
De manière schématique, dans un Dijkstra classique, on fait grossir une boule centrée sur la source, et on s’arrête lorsque la destination est incluse dans cette boule. Dans un Dijkstra bidirectionnel, on fait grossir tour à tour deux boules, une centrée sur la source et une centrée sur la destination, jusqu’à ce que ces deux boules se touchent. La surface des boules représentant schématiquement le temps de calcul, il est facile de s’imaginer que le Dijkstra bidirectionnel doit être plus rapide dans le cas où les graphes ne sont pas trop bizarres.
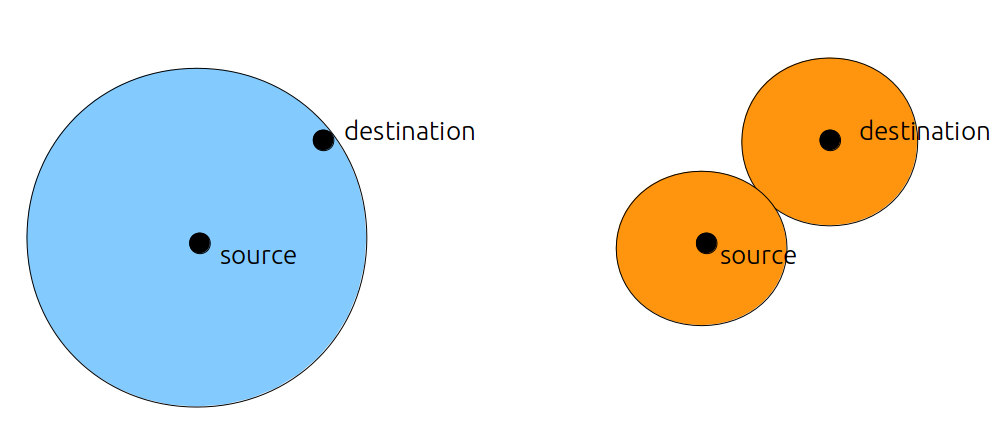
Nous allons commencer par une implémentation naïve, qui consiste à dire que, dès que les deux boules se touchent, on a trouvé le chemin. La distance est alors calculée comme la somme des distances de la source et de la destination vers le seul sommet qui appartient aux deux boules. Nous verrons plust tard, dans l’exercice 3.2, pourquoi cette solution est naïve.
Ouvrez le squelette de la classe BiDijkstra qui contient
les champs suivants :
final Graph g contenant le graphe,final int source contenant la source,final int dest contenant la destination,final Dijkstra forward représentant la recherche de
plus courts chemins à partir de la source,final Dijkstra backward représentant la recherche de
plus courts chemins à partir de la destination,Dijkstra currentDijkstra, otherDijkstra indiquant le
sens de la prochaine itération et celui opposé,private int last contenant le sommet traité par la
dernière itération,private Fenetre f nécessaire pour l’affichage graphique
(vous n’aurez pas à vous soucier de l’initialisation de ce champ).Complétez
BiDijkstra(Graph g, int source, int dest) de votre
classe. On veillera à ce que chaque champ soit correctement initialisé.
En particulier, la recherche backward doit s’effectuer sur le
graphe inversé et avec les sommets source et destination permutés.void flip() qui inverse la
direction de la recherche, en échangeant currentDijkstra et
otherDijkstra.void oneStep() qui réalise
une itération dans le sens de la recherche actuel et met à jour le champ
last.boolean isOver() qui
renvoie true si le sommet last a été traité
par la recherche forward et par la recherche backward.
Dans ce cas, on peut arrêter les itérations de Dijkstra. En effet, on a
trouvé un chemin entre source et dest, qui
passe par le sommet last.int getMinPath() qui
renvoie le poids du chemin obtenu passant par last. On
appellera cette fonction lorsque isOver() aura renvoyé
true.int compute() qui réalise
l’algorithme de Dijkstra bidirectionnel. Vous utiliserez bien entendu
les méthodes que vous venez d’écrire. L’algorithme devient très simple :
tant qu’il faut continuer la recherche, faire une itération, puis
changer la direction. Une fois la recherche terminée, renvoyer la valeur
d’un plus court chemin.Testez vos méthodes avec la classe Test31 dans
le fichier Test31.java. Vous devez
obtenir :
Test 3.1 : test de l'algorithme de Dijkstra bidirectionnel naif
Loading road networks from file data/mini.gr... done
Test du constructeur BiDijkstra(Graph, int, int)... [OK]
Test de la methode flip()... [OK]
Test de la methode oneStep()... [OK]
Test de la methode isOver()... [OK]
Test de la methode compute()... [OK]
Test de la methode getMinPath()... [OK]
Loading road networks from file data/USA-road-d-NY.gr... done
Loading geometric coordinates from file data/USA-road-d-NY.co ... done
Test de la methode getMinPath()... [OK]Exécutez la classe Test31bis dans le fichier Test31bis.java.
Vous devez voir avancer vos deux paquets de points traités (en rouge) et
leurs frontières (en vert) :
et obtenir le chemin :
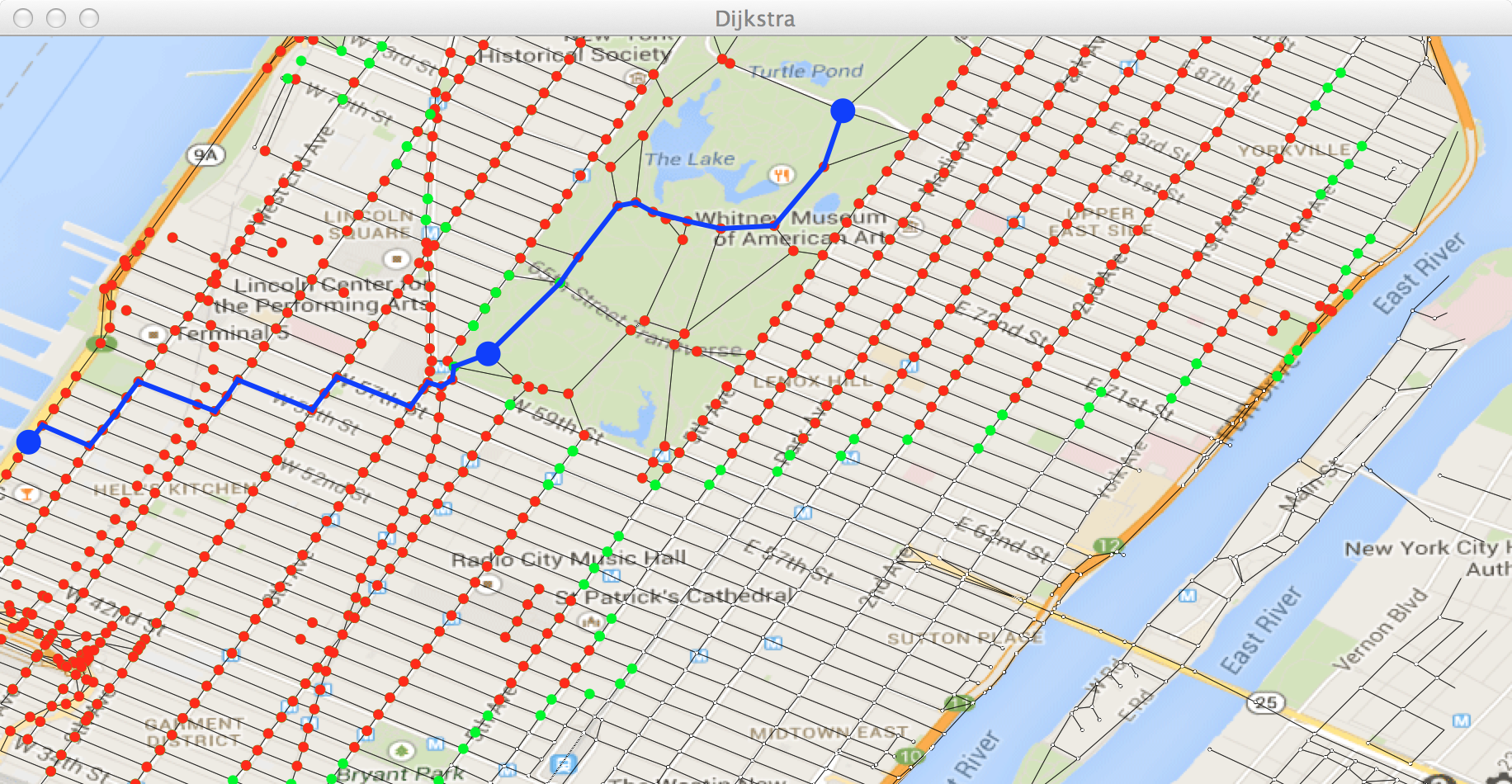
Sur ce chemin, le point last est le gros point bleu
central. Dans la console, vous devriez obtenir :
Loading background image from file data/NY_Metropolitan.png ... done
longueur chemin forward entre 190637 et 187333 = 39113
longueur chemin backward entre 190637 et 187333 = 39113
longueur chemin BiDijkstra entre 190637 et 187333 = 39113Déposez le fichier BiDijkstra.java
Exécutez maintenant la classe Test32bis dans le
fichier Test32bis.java, dans
lequel nous avons changé le point source. Vous devez voir
s’afficher :

et obtenir le chemin :

Dans la console, vous devriez obtenir :
Test 3.2 : test de l'algorithme de Dijkstra bidirectionnel
Loading road networks from file data/USA-road-d-NY.gr... done
Loading geometric coordinates from file data/USA-road-d-NY.co ... done
Loading background image from file data/NY_Metropolitan.png ... done
longueur chemin forward entre 190637 et 187333 = 35478
longueur chemin backward entre 190637 et 187333 = 35478
longueur chemin bidijkstra entre 190637 et 187333 = 35489Quelle anomalie constatez vous ? En effet, examinons le schéma suivant :
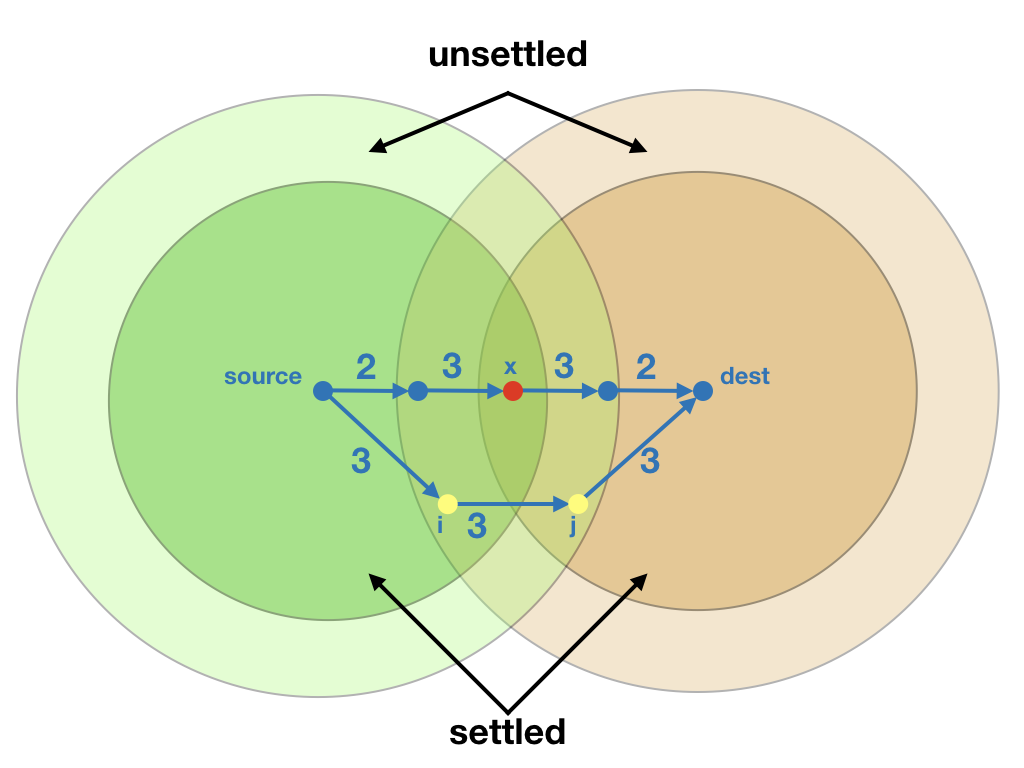
Dès lors que le sommet x a été traité par les deux
recherches, nous avons un candidat potentiel au plus court chemin entre
la source et la destination : l’union des plus courts chemins obtenus
entre la source et x et entre x et la
destination. Pourtant, il se peut que ce chemin ne soit pas le plus
court. En effet, un chemin plus court peut exister comme illustré dans
le dessin ci-dessus, à condition que
dist(source, i) + dist(j, dest) +
weight(i, j) < dist(source, x) +
dist(x, dest).
On peut alors démontrer (preuve plus bas) le fait suivant :
Soit
xl’unique sommet, tel queforward.settled[x]=backward.settled[x]=true.Soit
aun des chemins les plus courts desourceàdest, tel quelength(a)<forward.dist[x]+backward.dist[x].Alors le dernier point
isura(partant desource), tel queforward.settled[i]=true, est dansbackward.unsettledetlength(a)=forward.dist[i]+backward.dist[i].
Modifiez votre méthode int getMinPath()
afin qu’elle vérifie s’il existe un chemin plus court comme indiqué
ci-dessus et si c’est le cas, mette à jour la variable last
avant de renvoyer la longueur du chemin le plus court.
Testez avec la classe Test32 dans le fichier Test32.java. Vous
devriez obtenir :
Test 3.2 : test de l'algorithme de Dijkstra bidirectionnel
Loading road networks from file data/USA-road-d-NY.gr... done
Test de la methode getMinPath()... [OK]
longueur chemin forward entre 190637 et 187333 = 35478
longueur chemin backward entre 190637 et 187333 = 35478
longueur chemin bidijkstra entre 190637 et 187333 = 35478Exécutez à nouveau la classe Test32bis.
Vous devez maintenant voir s’afficher :
et obtenir le chemin :
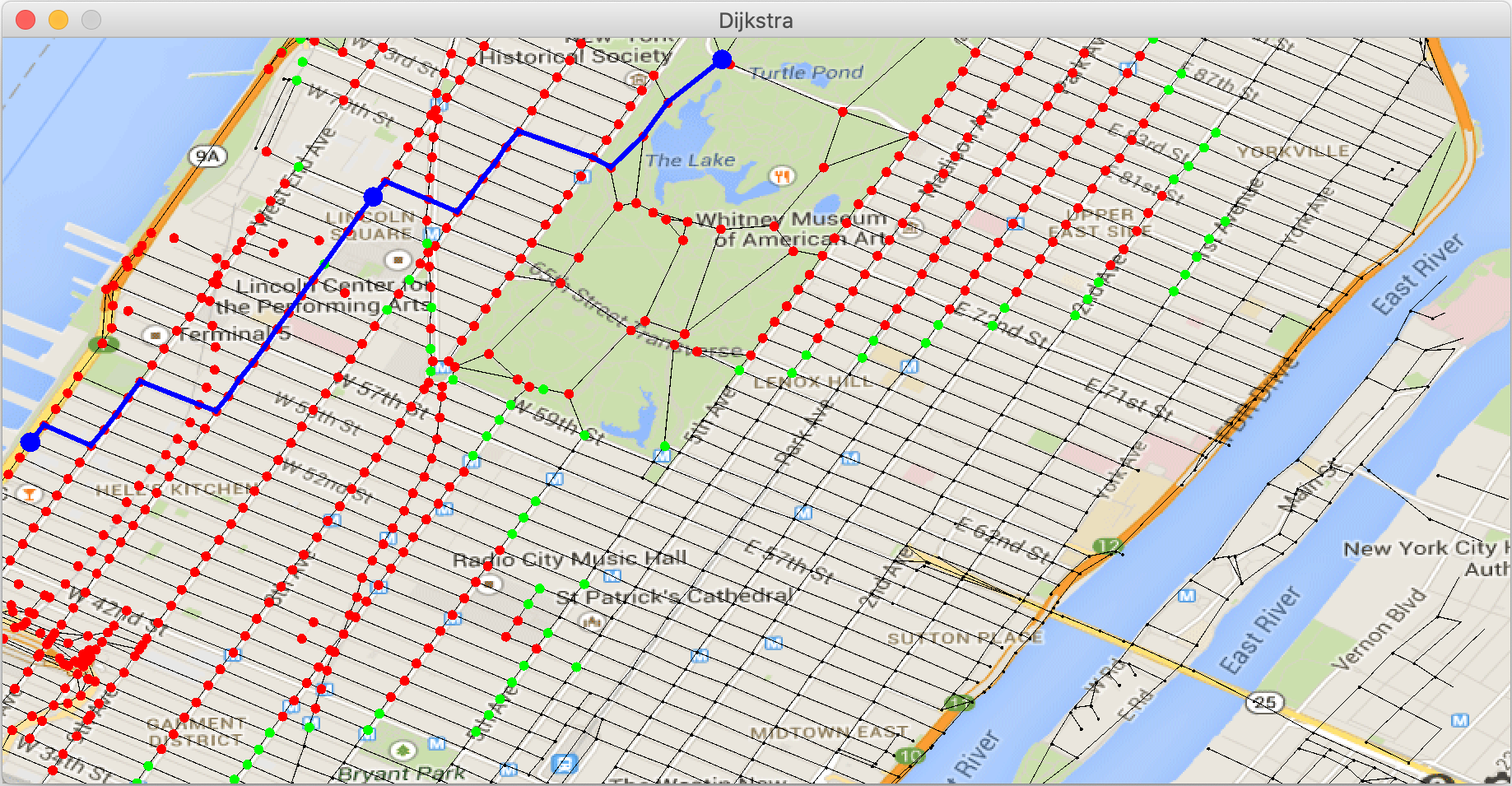
Dans la console, vous devriez obtenir :
Loading road networks from file data/USA-road-d-NY.gr... done
Loading geometric coordinates from file data/USA-road-d-NY.co ... done
Loading background image from file data/NY_Metropolitan.png ... done
longueur chemin forward entre 190637 et 187333 = 35478
longueur chemin backward entre 190637 et 187333 = 35478
longueur chemin bidijkstra entre 190637 et 187333 = 35478Déposez le fichier BiDijkstra.java
Afin de mesurer le gain d’efficacité de la version bidirectionnelle sur la version monodirectionnelle, nous allons compter le nombre d’itérations nécessaires dans chacun des cas.
Dans la classe Dijkstra, ajoutez un champ
int steps. Initialisez-le dans le constructeur, et
incrémentez-le dans la méthode oneStep().
Complétez les méthodes
public int getSteps () dans les deux
classes Dijkstra et BiDijkstra pour
qu’elles renvoient les nombres d’itérations correspondants.
Testez ce compteur avec le fichier Test4.java. Comparer le
nombre d’étapes nécessaires pour chacune des recherches. Vous devriez
obtenir :
Test 4 : comparaisons du nombre d'étapes
Loading road networks from file data/USA-road-d-NY.gr... done
Test de la methode getMinPath()... [OK]
longueur chemin forward entre 190636 et 187333 = 35478 nombre d'étapes = 1252
longueur chemin backward entre 190636 et 187333 = 35478 nombre d'étapes = 1204
longueur chemin BiDijkstra entre 190636 et 187333 = 35478 nombre d'étapes = 621Bien entendu, vous pouvez changer la source et la destination et relancer.
Déposez le fichier BiDijkstra.java
On voudrait démontrer le fait suivant :
Soit
xl’unique sommet, tel queforward.settled[x]=backward.settled[x]=true.Soit
aun des chemins les plus courts desourceàdest, tel quelength(a)<forward.dist[x]+backward.dist[x].Alors le dernier point
isura(partant desource), tel queforward.settled[i]=true, est dansbackward.unsettledetlength(a)=forward.dist[i]+backward.dist[i].
Preuve : Soit j le point qui suit
i sur a. Alors forward.settled[j]
= false et, par conséquence,
forward.dist[j] ≥ forward.dist[x]
(sinon j aurait été traité avant x).
Puisque a passe par j, nous avons
également
forward.dist[j] + backward.dist[j] ≤
length(a) < forward.dist[x] +
backward.dist[x].
Donc
backward.dist[j] < backward.dist[x].
Comme x est traité par backward, j est
aussi traité et donc i est bien dans
backward.unsettled. (Il n’est pas possible que
backward.settled[i] = true, car x
est l’unique tel sommet).
Puisque a passe par j, nous avons
forward.dist[i] + backward.dist[i] ≤
length(a).
Si cette inégalité était stricte, cela aurait voulu dire qu’il y a un
autre chemin de source (ou de dest) à
i plus court que celui, qui suit a. Mais alors
a ne serait pas parmi les plus courts chemins satisfaisant
les hypothèses du lemme. On conclut, donc, que
length(a) = forward.dist[i] +
backward.dist[i].