TD 6-7 : La théière et le lapin


Introduction
Arbres de recherche géométrique
L'objet de ces TDs est de réaliser plusieurs opérations de
recherche sur des modèles géométriques. Dans de nombreux cas, il existe des algorithmes simples qui permettent
d'effectuer ces recherches. Pour certaines applications, cependant,
ces algorithmes sont beaucoup trop lents. Au cours de ces TDs, nous allons
réaliser des algorithmes de recherche géométrique rapides au moyen
d'arbres de recherche.
Nous utiliserons deux icônes de la recherche en informatique graphique, la théière et le lapin, qui sont deux modèles géométriques fréquemment utilisés pour tester de nouveaux algorithmes de calcul d'images de synthèse, d'animations, etc. On a ainsi vu, par exemple, des théières chevelues et des lapins qui fondent! Vous pourrez trouver sur Wikipedia plus d'informations sur la théière et le lapin.
NB: l'énoncé contient
beaucoup d'indications. N'hésitez pas à le lire
attentivement !
Préliminaires
Classe(s), non ?
On déballe tout
Pour commencer, récupérez le fichier TD67-Programmes.zip (clic droit sur le lien), sauvez le dans le répertoire INF321/TD67/src/, et décompressez le dans ce répertoire (en tapant unzip TD67-Programmes.zip dans le terminal, dans ce répertoire).
Puis, sauvez les deux fichiers theiere.cdo et lapin.cdo dans le répertoire INF321/TD67/.
Enfin, vous ferez apparaître les fichiers dans Eclipse en faisant un clic droit sur votre projet (TD67) et en sélectionnant Refresh (ou en appuyant sur la touche F5).
Afin que vous puissiez vous concentrer sur les points importants, une grande partie des structures de données et des fonctions avec lesquelles nous allons travailler a déjà été écrite. Pour gagner du temps, ne lisez pas ces fichiers maintenant : les classes à examiner seront introduites au fur et à mesure de l'énoncé.
Elémentaire...
Commençons par examiner la classe Vecteur3 (fichier Vecteur3.java). Cette classe est très importante pour le TD, puisqu'elle sert à décrire les points de l'espace 3D (les champs x, y et z, de type double).
La classe Vecteur3 doit disposer de plusieurs méthodes pour manipuler des vecteurs. Commencez donc par compléter la classe Vecteur3 de sorte que, si a et b sont des Vecteur3, et d est un double alors:
-
a.plus(b) retourne une référence au vecteur a+b
-
a.moins(b) retourne une référence au vecteur a-b
-
a.fois(d) retourne une référence au vecteur d.a
-
a.produitVectoriel(b) retourne une référence au produit vectoriel a^b
-
a.produitScalaire(b) renvoie le produit scalaire de a et b
-
a.norme() renvoie la norme de a
-
a.norme2() renvoie le carré de la norme de a
-
a.normaliser() normalise le vecteur a (s'il est non nul)
-
a.ajouter(b) ajoute b au vecteur a
-
a.toString() renvoie la chaîne de caractères "[ 1.0 ] [ 2.0 ] [ 3.0 ]" si le vecteur a a pour composantes 1, 2 et 3
Vous pourrez ensuite utiliser ces méthodes pour faciliter l'écriture des réponses aux questions posées. Par exemple, la norme du vecteur ab (c'est-à-dire, le vecteur dont les extrémités sont a et b) est obtenue en faisant b.moins(a).norme().
De la même façon, pour calculer le vecteur r=(a-b)^(c+3.2*d), vous pourriez utiliser l'instruction:
Vecteur3 r=a.moins(b).produitVectoriel(c.plus(d.fois(3.2)));
qui tire parti du fait, par exemple, que a.moins(b) est de type Vecteur3, dont on peut utiliser la méthode produitVectoriel(...), etc.
Comme la classe Vecteur3 est essentielle dans ce TD, vous ferez particulièrement attention à vérifier vos réponses en écrivant un petit programme de test (par exemple dans une classe TestVecteur3, dont la fonction main effectuera des calculs sur les vecteurs).
Une fois la classe Vecteur3 terminée, vous déposerez le fichier Vecteur3.java :
Laaaaaaapin!
La classe Vecteur3 est utilisée par la classe Surface, pour décrire la géométrie d'une surface.
En effet, les surfaces considérées dans cette application sont des ensembles finis de triangles. On décrit donc la géométrie d'une surface par un ensemble de points (le tableau Vecteur3[] sommet de la classe Surface) et un ensemble de triangles (le tableau Triangle[] triangle de la classe Surface). Chaque objet de type Triangle contient simplement trois références aux sommets composant le triangle.
Ainsi, si lapin est de type Surface, alors
lapin.sommet[i]
est le sommet i du lapin (de type Vecteur3), et
lapin.triangle[j].a,
lapin.triangle[j].b,
lapin.triangle[j].c,
tous les trois de type Vecteur3, sont les références aux trois sommets du triangle j du lapin.
My beautiful teapot
Vous pouvez lancer le programme principal en faisant un clic droit sur le fichier TD67.java dans Eclipse, et en sélectionnant Run as/Java Application. La fenêtre suivante s'affiche à l'écran (Figure 1).

Figure 1. L'application initiale.
En cliquant dans la fenêtre principale, il est possible de modifier le point de vue (clic gauche: rotation; clic milieu: zoom; clic droit: translation). Les boutons "Rotation surface" et "Annuler rotation" permettent de modifier l'orientation de la surface affichée. Le bouton "Echanger surfaces" permet d'alterner entre la théière et le lapin.
Partie I - Construction des arbres de recherche
Introduction - Arbres de volumes englobants
Les arbres de recherche géométrique que nous allons utiliser sont des arbres (binaires) de volumes englobants. Ces arbres ont les propriétés suivantes:
-
Chaque noeud de l'arbre est une primitive géométrique simple (par la suite, une sphère) qui englobe (contient) une partie des triangles de la surface. La racine de l'arbre contient la totalité des triangles de la surface, et les feuilles de l'arbre contiennent chacune un triangle de la surface. Chaque triangle est associé à une et une seule feuille de l'arbre.
-
Chaque noeud interne de l'arbre contient les triangles contenus par ses deux noeuds fils.
Une deuxième classe très importante dans ce TD est donc la classe ArbreSpheres (fichier ArbreSpheres.java), qui décrit un noeud de l'arbre de recherche. Cette classe contient quatre champs :
-
un champ sphere qui est une référence à la sphère englobante (de type Sphere).
-
un champ triangle qui est une référence à un triangle de la surface (de type Triangle). Cette référence est différente de null pour les feuilles de l'arbre seulement.
-
un champ filsGauche qui est une référence au fils gauche du noeud (de type ArbreSpheres). Cette référence vaut null pour une feuille de l'arbre.
-
un champ filsDroit qui est une référence au fils droit du noeud (de type ArbreSpheres). Cette référence vaut null pour une feuille de l'arbre.
La figure 2A ci-dessous montre la structure des arbres binaires.
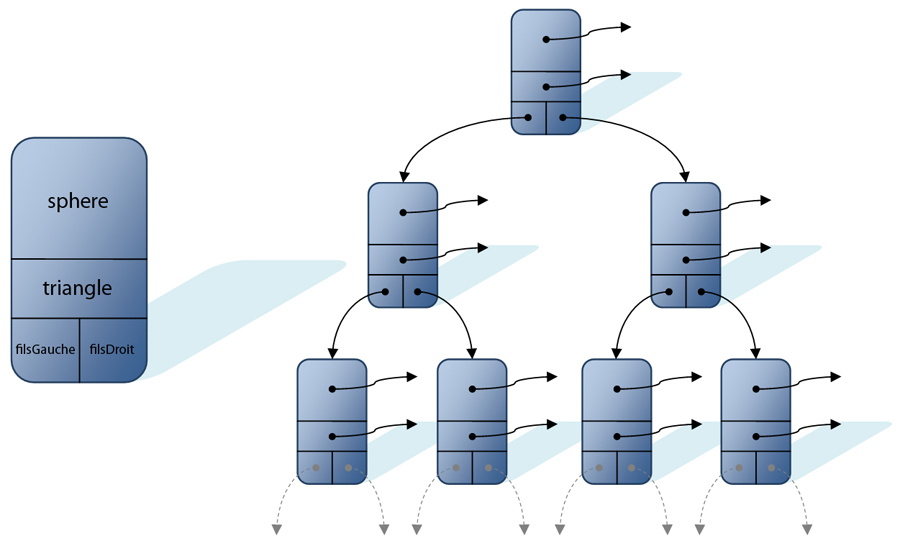
Figure 2A. La structure des arbres de recherche géométrique. A gauche, un objet de type ArbreSpheres. A droite, un arbre binaire.
La figure 2B montre les niveaux 0 (racine), 1, 2 et 13 d'un arbre de sphères englobantes associé à la théière.
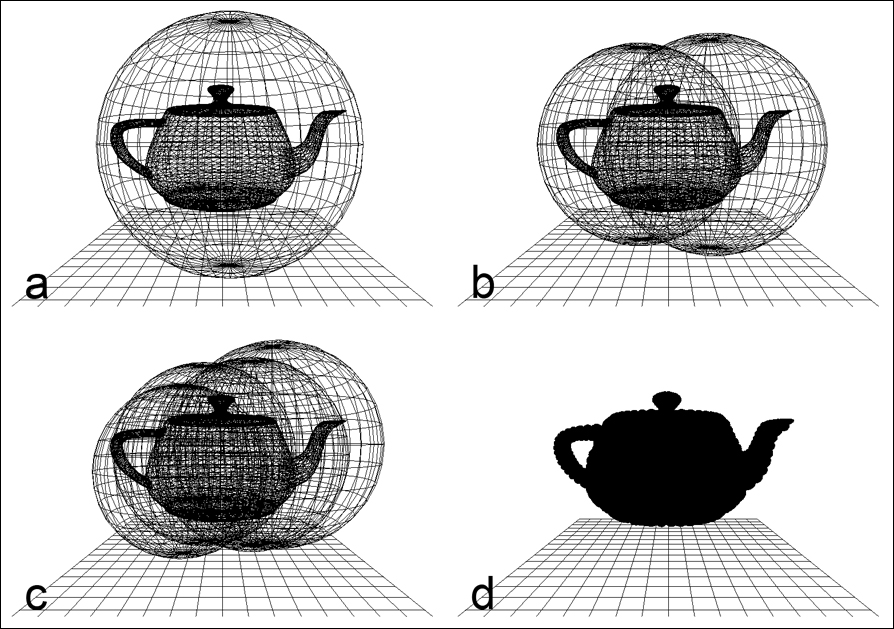
Figure 2B. Niveaux 0 (racine), 1, 2 et 13 d'un arbre de sphères englobantes associé à la théière.
Lors des recherches géométriques que nous allons effectuer, les volumes englobants vont nous permettre d'éliminer rapidement des sous-ensembles de triangles qui ne vérifient pas la propriété recherchée, et donc d'accélérer la recherche.
Important : à partir de maintenant, TOUTES les réponses du TD seront rédigées dans la classe TD67 (fichier TD67.java).
Question 1 - Tous en file
Afin de construire récursivement les arbres de sphères englobantes, il va falloir répartir un ensemble de triangles de la surface en deux sous-ensembles. Pour cela, nous allons utiliser des files de priorité afin d'ordonner des triangles. Ces files de priorité sont implémentées dans les classes NoeudFileTriangles, qui contient un noeud de la file, et FileTriangles, type enveloppé qui contient une référence à la tête de la file (champ head), et les fonctions de manipulation de la file dont nous aurons besoin dans ces TDs.
Notez que, pour simplifier, la même classe NoeudFileTriangles va être utilisée pour plusieurs questions du TD, et contient donc plusieurs champs (triangleA, etc.). Tous ces champs ne sont pas utilisés à chaque question. Par ailleurs, les noeuds de la file sont classés par priorité croissante (vous pouvez aller regarder la fonction insererTriangles de la classe FileTriangles, qui effectue une insertion dans la file de sorte que tous les éléments soient triés).
Commencez par compléter la fonction longueurFile(FileTriangles file) de la classe TD67, qui parcourt la file pour déterminer sa longueur.
|
Indice
Indice: on pourra utiliser une approche itérative (on utilisera un compteur longueur de type int et une variable noeudCourant de type NoeudFileTriangles pour parcourir la file, en partant de file.head). |
Dépose
Déposez le fichier TD67.java comportant la fonction complétée longueurFile(FileTriangles file).
Question 2 - Aïe, ça coupe !
Complétez maintenant la fonction dichotomie(FileTriangles file) de la classe TD67, qui coupe la file en deux et (crée et) renvoie une file qui commence à la moitié de la file initiale. Par exemple, si la file fileOrdonnee contient 5 éléments de priorités respectives -3.0, -1.7, 2.0, 12.1 et 27.3, l'instruction
FileTriangles moitieFile=TD67.dichotomie(fileOrdonnee);
réduit la file fileOrdonnee à ses deux premiers éléments (de priorités -3.0 et -1.7), et crée la file moitieFile qui contient les trois derniers éléments (de priorités 2.0, 12.1 et 27.3).
|
Indice 1
Indice 1 : on utilisera la fonction précédente pour connaître la longueur de la file (i.e., on appellera longueurFile(file)). Pour "couper" la file au noeud noeudCourant (de type NoeudFileTriangles), on mettra noeudCourant.suivant à null. (n'hésitez pas à faire un dessin!). |
|
Indice 2
Indice 2 : moitieFile sera un nouvel objet de type FileTriangles (créé avec new), mais les noeuds de la file initiale fileOrdonnee seront simplement déplacés vers moitieFile, sans être copiés (encore une fois, n'hésitez pas à faire un dessin!). |
Pour les cas où la file est de longueur inférieure ou égale à 1, on renverra null.
On pourra utiliser le programme TestFileTriangles.java pour tester la fonction dichotomie() (clic droit sur le fichier TestFileTriangles.java, puis Run as/Java Application). Le programme devra afficher les deux lignes suivantes:
-3.0 / -1.7 / null
2.0 / 12.1 / 27.3 / null
Dépose
Déposez le fichier TD67.java, qui comporte maintenant la fonction complétée dichotomie(FileTriangles file).
Question 3 - Construction de l'arbre
Nous allons maintenant pouvoir construire un arbre de sphères englobantes associé à la théière et au lapin. Pour cela, nous allons utiliser la classe Sphere, qui contient la description d'une sphère, et la classe ArbreSpheres, qui décrit un noeud de l'arbre de sphères englobantes.
Nous allons construire un arbre grâce à une fonction qui coupe récursivement en deux une file de triangles (tant que le nombre de triangles dans la file est plus grand que 1), et construit pour chaque file une sphère englobante. Cette fonction procède de la façon suivante:
Construction d'un arbre englobant les triangles contenus dans une file
-
Construire la sphère s englobant les triangles de la file
-
Si la file ne contient qu'un triangle t (dont la référence est alors file.head.triangleA)
-
Construire et renvoyer la feuille de l'arbre qui fait référence à s et t (filsGauche et filsDroit valent null)
-
-
Sinon
-
Couper la file file en deux sous-listes fileFilsGauche et fileFilsDroit
-
Construire les arbres filsGauche et filsDroit correspondants
-
Construire et renvoyer le noeud interne qui fait référence à s, filsGauche et filsDroit (rappel: triangle vaut null pour les noeuds internes)
-
Complétez la fonction construireArbreSpheresPourTrianglesDansFile(FileTriangles file) de la classe TD67,qui implémente l'algorithme ci-dessus.
Indice: on utilisera le constructeur Sphere maSphere=new Sphere(file); pour construire la sphère associée à la file de triangles file. Afin de couper la file file en deux sous-files fileFilsGauche et fileFilsDroit, on utilisera les deux lignes suivantes:
FileTriangles fileFilsGauche=file;
FileTriangles fileFilsDroit=dichotomie(file);
Une fois la fonction écrite, on pourra afficher les différents niveaux de l'arbre en cochant la case "Afficher arbre" de l'application. Les deux barres situées sous la case permettent de contrôler le niveau affiché et la qualité du dessin des sphères (un pas plus grand accélère le dessin). On pourra vérifier que les arbres des deux surfaces sont bien construits, en faisant varier le niveau affiché, et en cliquant sur "Echanger surfaces".
Dépose
Déposez le fichier complété TD67.java.
Question 4 - Un peu d'ordre
En affichant les arbres, on peut remarquer que les sphères ne sont pas très proches des surfaces qu'elles doivent englober. Ceci vient du fait que les triangles de la file ne sont pas triés en fonction de leurs positions (deux triangles proches dans l'espace ne sont pas proches dans la file). Par conséquent, couper la file de triangles en deux ne permet pas vraiment d'aboutir à des sphères filles plus petites.
Afin de corriger ce problème, complétez maintenant la fonction ordonnerTriangles(FileTriangles file) de la classe TD67, qui construit une nouvelle file de triangles (avec new, donc), ordonnée suivant les positions des centres de gravité des triangles. Pour cela, on commencera par choisir une direction aléatoire (un vecteur Vecteur3 dont les composantes seront choisies aléatoirement grâce à la fonction Math.random()), et on insèrera les triangles dans cette nouvelle file avec une priorité égale à la coordonnée de leur centre de gravité selon cette direction.
Une fois le centre de gravité du triangle calculé (centre), la coordonnée du centre de gravité dans la direction direction (de type Vecteur3) sera égale à centre.produitScalaire(direction). On insèrera donc le triangle dans la nouvelle file fileOrdonnee grâce à l'instruction suivante : fileOrdonnee.insererTriangles(noeudCourant.triangleA,null,null,centre.produitScalaire(direction));
|
Indice 1
Indice 1 : puisque l'on souhaite ordonner les triangles en fonction de la projection de leur centre de gravité sur un axe il faudra, pour chaque triangle de la file, calculer les coordonnées de son centre de gravité (vous pourrez utilisez les méthodes de la classe Vecteur3). |
|
Indice 2
Indice 2 : on utilisera une variable noeudCourant pour parcourir la file. |
Une fois la fonction écrite, on l'appellera depuis la fonction construireArbreSpheresPourTrianglesDansFile(FileTriangles file) avant la dichotomie :
file=ordonnerTriangles(file);
FileTriangles fileFilsGauche=file;
FileTriangles fileFilsDroit=dichotomie(file);
On pourra ensuite afficher les arbres pour constater que les sphères convergent plus rapidement vers la surface des objets.
Dépose
Déposez le fichier TD67.java comportant la fonction ordonnerTriangles(FileTriangles file) complétée.
Partie II - Détection de collisions
Introduction
Dans de nombreuses applications (jeux vidéo, animation, réalité virtuelle, robotique, conception assistée par ordinateur, etc.), il est nécessaire de détecter des collisions entre des objets virtuels. Par exemple, dans un jeu vidéo, on souhaite détecter des collisions entre les personnages et les murs ou les objets du décor.
Afin de détecter les collisions rapidement, une méthode classique consiste à utiliser des arbres de volumes englobants. Dans le cas d'une détection de collisions entre une surface et un mur, par exemple, on procède de la manière suivante:
-
Si la sphère englobant complètement la surface (i.e., la sphère à la racine de l'arbre associé à la surface) ne pénètre pas le mur, il est certain qu'il n'y a pas de collisions entre la surface et le mur (puisque la surface est contenue dans la sphère).
-
Sinon, la surface est peut-être en collision avec le mur (peut-être seulement, puisque la surface n'est que contenue dans le volume englobant, et l'inclusion peut être stricte). On précise alors la recherche en détectant des collisions entre les noeuds fils et le mur. On poursuit la recherche récursivement, en descendant seulement dans les parties de l'arbre qui sont en collision avec le mur.
Les sphères englobantes sont des primitives géométriques simples, pour lesquelles il est facile de déterminer une intersection avec d'autres primitives géométriques (par exemples des sphères ou des demi-espaces). Grâce à cette propriété (et à la propriété de contenance), l'arbre de sphères englobantes permet de localiser rapidement les collisions éventuelles entre la surface et le mur.
Question 5 - Intersection boule / demi-espace
Pour simplifier, nous allons considérer le cas d'un mur infini (i.e., un demi-espace). Commencez par compléter la fonction intersectionSphereDemiEspace(Sphere s, Vecteur3 point, Vecteur3 normale) de la classe TD67, qui renvoie true si et seulement si la sphère s (plus exactement, la boule correspondante) est au moins partiellement contenue dans le demi-espace défini par un point et une normale, c'est-à-dire l'ensemble { x : (x-point).normale<=0) }, où le . désigne le produit scalaire (en d'autres termes, la frontière du demi-espace est le plan passant par point, et orthogonal à normale). Notez qu'avec cette définition, la normale est à l'extérieur du demi-espace. Par la suite, toutes les normales considérées seront de norme 1.
|
Indice 1
Indice 1: Faites un dessin ! On n'oubliera pas de prendre en compte le rayon de la sphère ! |
|
Indice 2
Indice 2: N'oubliez pas que (x-point).normale représente la distance signée (i.e. positive ou négative) entre le point x et le plan passant par point et orthogonal au vecteur normale. |
|
Indice 3
Indice 3 : n'hésitez pas à utiliser les méthodes moins et produitScalaire de la classe Vecteur3 pour simplifier l'écriture de la fonction. |
Dépose
Déposez le fichier TD67.java comportant la fonction intersectionSphereDemiEspace(...) complétée.
Question 6 - Ça passe ou pas ?
Grâce à la fonction écrite à la question précédente, écrivez une fonction récursive de parcours de l'arbre de sphères englobantes qui retourne true lorsque la surface est partiellement contenue dans un demi-espace. On l'a dit, ce genre de fonctions est notamment utilisé dans les jeux vidéo pour détecter des collisions entre les joueurs (ou les objets de la scène), et les murs du décor.
Plus précisément, complétez la fonction récursive intersectionSurfaceMurVraiFaux(ArbreSpheres arbre, Vecteur3 point, Vecteur3 normale) de la classe TD67, qui parcourt l'arbre associé à la surface. Comme indiqué précédemment, on ne descendra que dans les parties de l'arbre susceptibles de contenir des triangles qui pénètrent le mur, c'est-à-dire les noeuds de l'arbre dont la sphère pénètre le mur. Pour les feuilles de l'arbre qui pénètrent le demi-espace, on détectera une collision entre le triangle référencé par la feuille et le demi-espace.
|
Indice 1
Indice 1: il suffit de programmer l'algorithme décrit en introduction de la partie II. |
|
Indice 2
Indice 2 : parce qu'il est convexe, un triangle est au moins partiellement contenu dans un demi-espace si et seulement si au moins l'un de ses points est dans le demi-espace (rappel: les sommets (de type Vecteur3) du triangle référencé par une feuille arbre sont arbre.triangle.a, arbre.triangle.b, et arbre.triangle.c). |
|
Indice 3
Indice 3 : si votre fonction n'a pas le résultat attendu, peut-être que le problème vient de la fonction intersectionSphereDemiEspace(...). |
On pourra vérifier le résultat en cliquant sur le bouton "Intersection plan V/F", qui génère un demi-espace aléatoire et appelle la fonction intersectionSurfaceMurVraiFaux(...), et en faisant tourner la surface. Lorsqu'il y a collision, la surface devient entièrement verte (Figure 3). Notez que la normale au mur est dessinée à l'extérieur du demi-espace.
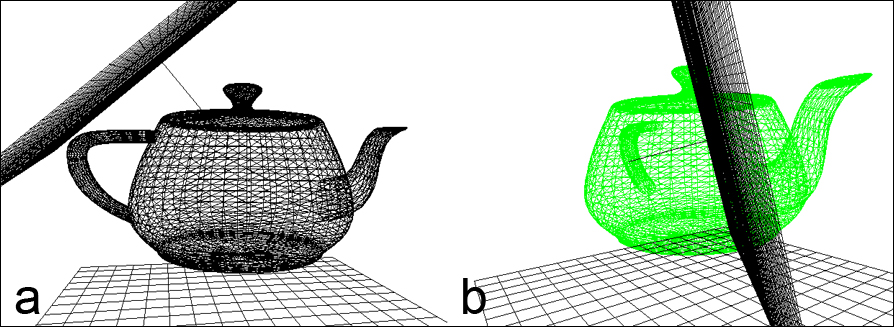
Figure 3. Détection de collisions entre une surface et un mur (demi-espace). a : la surface ne pénètre pas le mur. b: collision.
Dépose
Déposez le fichier TD67.java, qui comporte maintenant la fonction intersectionSurfaceMurVraiFaux(...) complétée.
Question 7 - Triangles, au rapport !
On cherche maintenant à connaître l'ensemble des triangles qui pénètrent le demi-espace. En vous inspirant de la fonction précédente, complétez la fonction intersectionSurfaceMur(ArbreSpheres arbre, Vecteur3 point, Vecteur3 normale, FileTriangles file) de la classe TD67. Notez que, contrairement à la fonction précédente, il ne sera pas possible de terminer dès que l'on détectera une interpénétration entre un triangle de la surface et le demi-espace.
On utilisera la fonction insererTriangles(...) de la file passée en paramètre. Ainsi, si l'on détecte une interpénétration entre le triangle arbre.triangle et le demi-espace, on utilisera l'instruction file.insererTriangles(arbre.triangle,null,null,0.0); pour insérer le triangle dans la file.
On pourra vérifier le résultat en cliquant sur le bouton "Intersection plan", qui génère un demi-espace aléatoire et appelle la fonction intersectionSurfaceMur(...), et en faisant tourner la surface. Lorsqu'il y a collision, les triangles qui pénètrent le demi-espace s'affichent en vert (Figure 4).

Figure 4. Détection de collisions entre une surface et un mur (demi-espace). Les triangles qui pénètrent le mur s'affichent en vert.
Dépose
Déposez le fichier TD67.java, qui comporte maintenant la fonction intersectionSurfaceMur(...) complétée.
Question 8 - Poly...? Poly...? Polyèdre !
En vous inspirant de la fonction précédente, complétez la fonction intersectionSurfacePolyedre(ArbreSpheres arbre, int nFaces, Vecteur3[] point, Vecteur3[] normale, FileTriangles file) de la classe TD67, qui retourne l'ensemble des triangles d'une surface qui sont entièrement contenus dans un polyèdre convexe.
Le polyèdre est défini comme l'intersection des demi-espaces 0, 1, ..., nFaces-1 (i.e., le demi-espace i est défini par le point point[i] et la normale normale[i]). Lisez bien la question ! On cherche les triangles entièrement contenus dans le polyèdre.
Attention : une approche consisterait à faire nFaces appels à la fonction implémentée à la question précédente, et à faire l'intersection des files retournées... Pourquoi cette approche est-elle fausse (soyez attentifs) ? Pourquoi, de plus, cette approche serait-elle inefficace ?
On pourra vérifier le résultat en cliquant sur le bouton "Intersection polyedre", qui génère un polyèdre aléatoire et appelle la fonction intersectionSurfacePolyedre(...), et en faisant tourner la surface. Lorsqu'il y a collision, les triangles entièrement contenus dans le polyèdre s'affichent en vert (Figure 5).
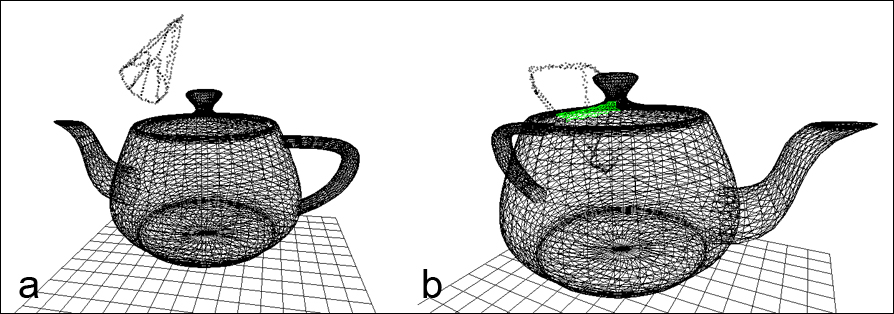
Figure 5. Calcul des triangles contenus dans un polyèdre. a : pas d'intersection. b: les triangles entièrement contenus dans le polyèdre sont affichés en vert.
Dépose
Déposez le fichier TD67.java, qui comporte maintenant la fonction complétée intersectionSurfacePolyedre(...).
Question 9 - Au minimum...
Il est parfois nécessaire de calculer le point extrémal d'une surface dans une direction (par exemple pour calculer un volume englobant la surface, ou pour détecter une collision entre la surface et un demi-espace). Complétez la fonction récursive minimumSurface(ArbreSpheres arbre, Vecteur3 minimumCourant, Vecteur3 normale) de la classe TD67, qui parcourt l'arbre associé à la surface pour déterminer le sommet s de la surface qui minimise le produit scalaire s.normale. On s'arrangera pour que, lorsque la fonction termine, la (mémoire référencée par la) variable minimumCourant contienne une copie des coordonnées du sommet recherché.
Attention : vous devez essayer d'éviter un parcours exhaustif de l'arbre ! Pour cela, vous pouvez éviter de parcourir les parties de l'arbre dont on est certain qu'elles ne contiennent pas de meilleur candidat que minimumCourant. Bien sûr, ceci peut être détecté grâce à la sphère englobante associée au noeud arbre.
Note : la fonction minimumSurface(ArbreSpheres arbre, Vecteur3 minimumCourant, Vecteur3 normale) prend une référence minimumCourant à un vecteur. Ce vecteur doit contenir une copie des coordonnées du sommet qui correspond au minimum courant. Lorsque la fonction minimumSurface(...) est appelée pour la première fois, minimumCourant contient une copie des coordonnées du premier sommet de la surface.
|
Indice 1
Indice 1 : la fonction cherche récursivement un meilleur minimum que le minimumCourant, tout en évitant de perdre du temps dans les régions de la surface inintéressantes. |
On pourra vérifier le résultat en cliquant sur le bouton "Minimum", qui génère une direction aléatoire et appelle la fonction minimumSurface(...), et en faisant tourner la surface. Le plan dessiné devra être tangent à la surface (Figure 6). NB : la fonction minimumSurface est appelée (lorsque l'on clique sur "Minimum ") en passant en premier minimumCourant le sommet 0 de la surface affichée.

Figure 6. Calcul du point extrémal dans une direction.
Une fois la fonction minimumSurface écrite, on pourra également cliquer sur le bouton "Ajuster sol", qui modifie la position du sol pour l'amener en contact avec la surface (Figure 7).

Figure 7. La fonction minimumSurface permet également d'ajuster la position du sol (en cliquant sur "Ajuster sol").
Dépose
Déposez le fichier TD67.java, qui comporte maintenant la fonction complétée minimumSurface(...).
Partie III - Lancer de rayons
Introduction
Une méthode classique de calcul d'images de synthèse est celle du lancer de rayons (ray-tracing). Cette méthode simule le parcours inverse des rayons lumineux, en partant de l'oeil de l'observateur jusqu'aux sources de lumière, afin de déterminer la couleur de chaque point de l'écran. Afin de calculer rapidement des images de synthèse de cette façon, il est important d'être capable de rechercher très efficacement l'ensemble des triangles d'une surface traversés (touchés) par un rayon lumineux. Vous l'avez deviné, nous allons utiliser les arbres de sphères englobantes pour effectuer ces recherches.
Pour cela, nous allons utiliser la classe Rayon pour représenter un rayon lumineux. Un rayon lumineux est simplement une demi-droite, qui a un pointDeDepart (de type Vecteur3) et une direction (de type Vecteur3 également).
Question 10 - Aïe, ça pique !
Complétez la fonction intersectionSurfaceRayonVraiFaux(ArbreSpheres arbre, Rayon rayon) de la classe TD67, qui renvoie true si et seulement si le rayon rayon coupe la surface. Cette fonction sera utilisée par le lanceur de rayons pour déterminer si un point est dans une zone d'ombre (il suffit de savoir si une surface est entre la source de lumière et le point).
Lorsque le rayon coupera une sphère feuille, on utilisera la fonction intersectionTriangle(Vecteur3 a, Vecteur3 b, Vecteur3 c, Vecteur3 i) de la classe Rayon, qui renvoie true lorsqu'il y a intersection entre le rayon et le triangle abc, et qui, le cas échéant, copie dans i le point d'intersection. On utilisera donc cette fonction de la façon suivante:
Vecteur3 pointIntersection=new Vecteur3();
boolean
intersection=rayon.intersectionTriangle(a,b,c,pointIntersection);
et l'on récupèrera, si intersection vaut true, la position du point d'intersection dans pointIntersection (qui ne sert que dans la question suivante).
On utilisera la fonction intersectionSphere(Sphere s) de la classe Rayon, qui renvoie true lorsque le rayon coupe la sphère s. Bien sûr, on ne descendra que dans les parties de l'arbre qui contiennent des triangles susceptibles d'être coupés par le rayon.
On pourra vérifier le résultat en cliquant sur le bouton "Intersection rayon V/F", qui génère un rayon aléatoire et appelle la fonction intersectionSurfaceRayonVraiFaux(...), et en faisant tourner la surface (Figure 7).
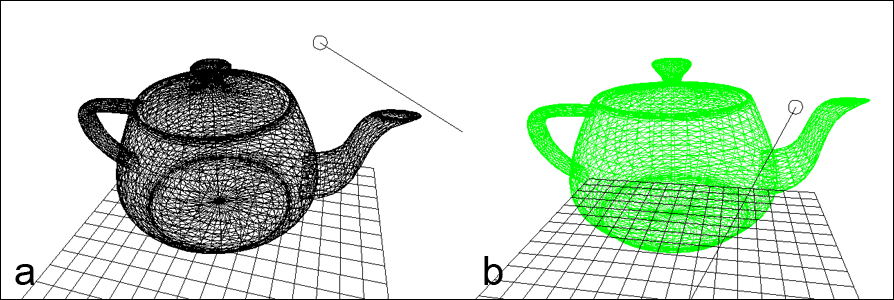
Figure 7. Détection d'une intersection entre un rayon et une surface.
Egalement, on pourra tester la fonction en cliquant sur "Ray-trace Mono", qui appelle le lanceur de rayon "monochrome". Ce lanceur de rayons utilise la fonction intersectionSurfaceRayonVraiFaux(...) et peut donc seulement déterminer si le rayon qui part de l'oeil coupe une surface ou non. Si le rayon coupe la surface, le lanceur de rayons affiche un point de la couleur de l'objet; sinon, il affiche un point bleu (le ciel) (Figure 8). Ce lanceur est donc appelé "monochrome" puisque l'objet est uniformément coloré.
NB : il est possible de changer le "pas" du ray-tracer afin d'accélérer les calculs.

Figure 8. Le lanceur de rayons "monochrome" utilise la fonction intersectionSurfaceRayonVraiFaux(...) pour calculer une image simple.
Dépose
Déposez le fichier TD67.java, qui comporte maintenant la fonction complétée intersectionSurfaceRayonVraiFaux(...).
Question 11 - Ça pique ? Où ça ?
Afin de calculer des images plus réalistes, il est nécessaire de connaître la position des points d'intersection entre le rayon et la surface. Plus exactement, il est nécessaire de connaître le point de la surface le plus proche de l'oeil.
En vous inspirant de la fonction précédente, complétez la fonction intersectionSurfaceRayon(ArbreSpheres arbre, Rayon rayon, FileTriangles file) de la classe TD67, qui insère les triangles coupés par le rayon dans la file. Contrairement à la question précédente, il ne suffira donc plus d'arrêter la recherche dès qu'un triangle a été trouvé.
Parce que le lanceur de rayons a besoin de connaître à la fois la position du point d'intersection et une référence au triangle, on insèrera les triangles dans la file de la façon suivante:
file.insererTriangles(arbre.triangle,null,pointIntersection,d);
où d est la distance (que l'on aura calculée) du point d'intersection à l'oeil (i.e., le pointDeDepart du rayon).
|
Indice
Indice : On pourra utiliser... Euh, non, pour cette question, vous ne devriez pas avoir besoin d'indices... |
On pourra vérifier le résultat en cliquant sur le bouton "Intersection rayon", qui génère un rayon aléatoire et appelle la fonction intersectionSurfaceRayon(...), et en faisant tourner la surface (Figure 9). Les triangles coupés par le rayon s'afficheront en vert.

Figure 9. Détection d'une intersection entre un rayon et une surface. Les triangles coupés par le rayon sont affichés en vert.
On pourra enfin tester la fonction en cliquant sur "Ray-trace Normal", qui appelle le lanceur de rayon pour calculer une image (les curieux pourront examiner la fonction rayTraceSurface(Graphics g, int surfaceIndex) de la classe InterfaceA). Contrairement au lanceur de rayons monochrome, ce lanceur de rayons utilise les deux fonctions précédentes pour déterminer la couleur de chaque point et les zones d'ombres (Figure 10).
Rappel : il est possible de changer le "pas" du ray-tracer afin d'accélérer les calculs.

Figure 10. Le lanceur de rayons utilise les deux fonctions précédentes pour calculer la couleur de chaque point de l'écran, et les zones d'ombres.
On pourra utiliser les boutons "Rotation surface" (et, éventuellement, "Ajuster sol") pour modifier l'orientation de la surface et faire varier les images.
Dépose
Déposez le fichier TD67.java, qui comporte maintenant la fonction complétée intersectionSurfaceRayon(...).
Question 12 - En effet...
Afin d'apprécier l'apport des arbres de sphères englobantes, réécrivez les deux fonctions précédentes en utilisant chaque fois un algorithme linéaire, qui parcourt la liste entière des triangles pour effectuer la recherche.
Complètez ainsi les deux fonctions
intersectionSurfaceRayonVraiFauxLineaire(Surface surface, Rayon
rayon) et intersectionSurfaceRayonLineaire(Surface surface,
Rayon rayon, FileTriangles file) de la classe TD67.
Une fois ces deux fonctions écrites, on comparera la vitesse d'exécution des
deux types de lanceurs de rayons (optimisé et linéaire) en utilisant les
boutons "Ray-trace Normal" et "Ray-trace
Lineaire" (Figure 11).
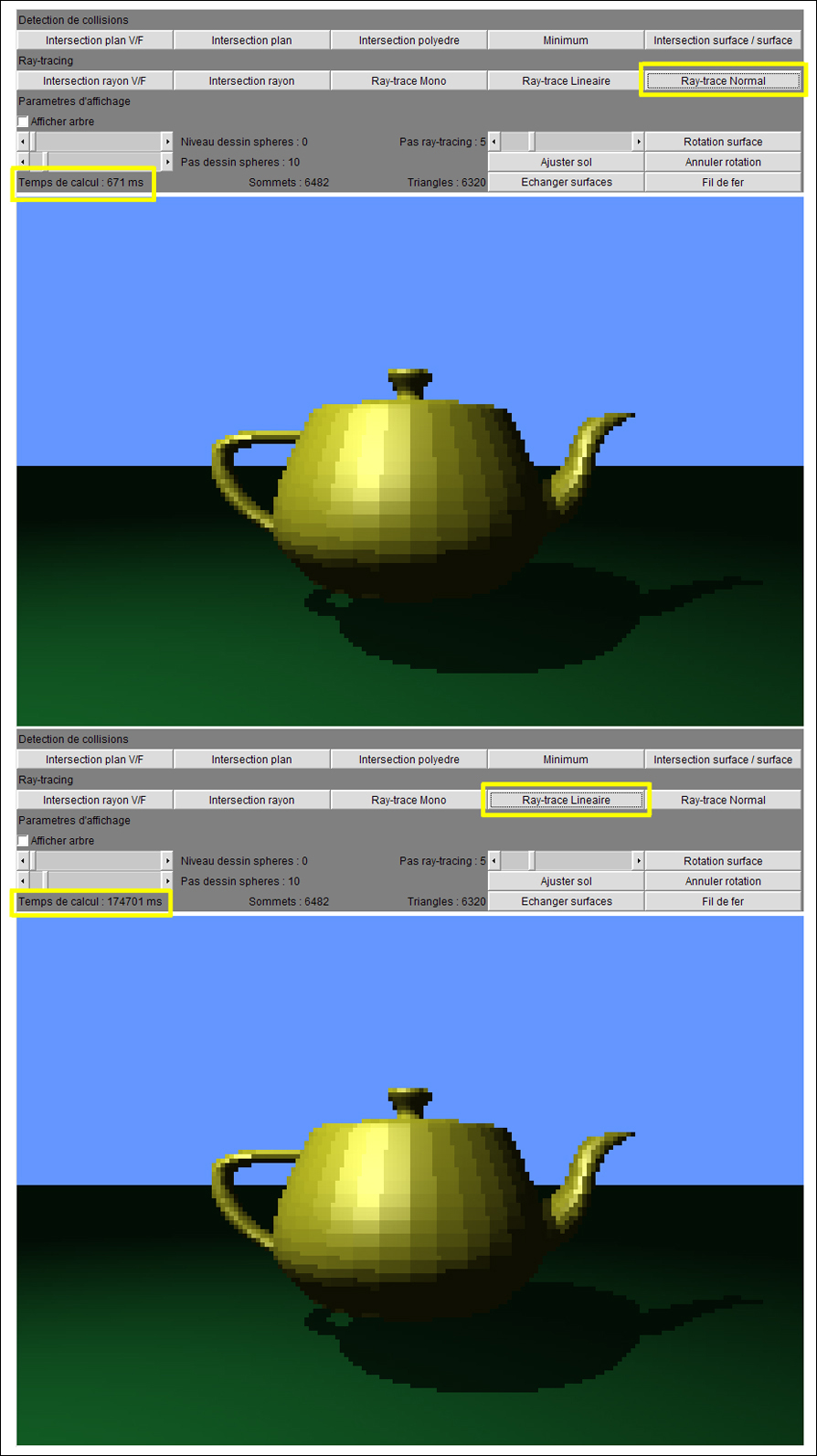
Figure 11. Le lanceur de rayons linéaire est beaucoup plus lent que le lanceur de rayons utilisant les arbres de sphères englobantes. Même avec un "pas" de 5, le lanceur linéaire prend 175 secondes, contre 0.7 secondes pour le lanceur optimisé.
Dépose
Déposez le fichier TD67.java, qui comporte maintenant les fonctions complétées intersectionSurfaceRayonVraiFauxLineaire(...) et intersectionSurfaceRayonLineaire(...).
Partie IV - Détection de collisions avancée
Introduction - Ça se complique...
Dans les questions précédentes, il existait des algorithmes linéaires simples pour effectuer les recherches demandées (puisqu'il suffit de parcourir la liste des triangles de la surface). Nous allons maintenant accélérer des recherches de complexité quadratique : la détection de collisions entre deux surfaces triangulées.
Soient deux surfaces triangulées A et B composées respectivement de nA et nB triangles. On cherche à déterminer la liste des paires ("triangle tA de la surface A","triangle tB de la surface B") de triangles dont l'intersection est non vide. La complexité de ce problème est bien quadratique, puisque dans le cas le pire le nombre d'intersections est nA x nB.
Question 13 - Détection de collisions entre sphères
Commencez par compléter la fonction boolean intersectionSphereSphere(Sphere sA, Sphere sB) de la classe TD67, qui renvoie true si et seulement si la sphère sA recouvre la sphère sB (plus exactement, on souhaite détecter une intersection entre les boules correspondantes).
|
Indice
Indice: Faites un dessin. |
Dépose
Déposez le fichier TD67.java, qui comporte maintenant la fonction complétée intersectionSphereSphere(...).
Question 14 - Bim, bam, boum...
Complétez la fonction intersectionSurfaceSurface(ArbreSpheres arbreA, ArbreSpheres arbreB, FileTriangles file) de la classe TD67, qui détecte une collision entre deux surfaces et renvoie une liste de paires de triangles en collision. Plus précisément, écrivez une fonction récursive qui traverse simultanément les deux arbres de sphères englobantes, afin de déterminer la liste des paires de triangles en collision. Pour deux arbres donnés, la fonction effectuera un test de recouvrement entre les sphères situées à la racine des arbres, afin de déterminer si une collision entre les géométries englobées par les arbres peut exister. Si c'est le cas, la fonction raffinera la recherche si c'est possible (en traversant les descendants des arbres) ou bien effectuera un test d'intersection entre les triangles contenus dans les arbres (qui seront alors des feuilles).
Afin de déterminer s'il y a intersection entre deux triangles, on utilisera la fonction intersectionTriangleTriangle(Vecteur3 a, Vecteur3 b, Vecteur3 c, Vecteur3 d, Vecteur3 e, Vecteur3 f) de la classe Triangle, qui renvoie true si et seulement s'il existe une intersection entre les triangles abc et def. Cette fonction est déjà écrite et on l'utilisera en écrivant, par exemple :
boolean intersection=Triangle.intersectionTriangleTriangle(a,b,c,d,e,f);
Le cas échéant, on signalera cette intersection en l'insérant dans la file de la façon suivante:
file.insererTriangles(arbreA.triangle,arbreB.triangle,null,0.0);
|
Indice
Indice : mmmm... Non. |
On pourra vérifier le résultat en cliquant sur le bouton "Intersection surface / surface", qui génère une position aléatoire pour la seconde surface et appelle la fonction intersectionSurfaceSurface(...), et en modifiant le point de vue (Figure 12). Les paires de triangles en intersection s'afficheront en vert.
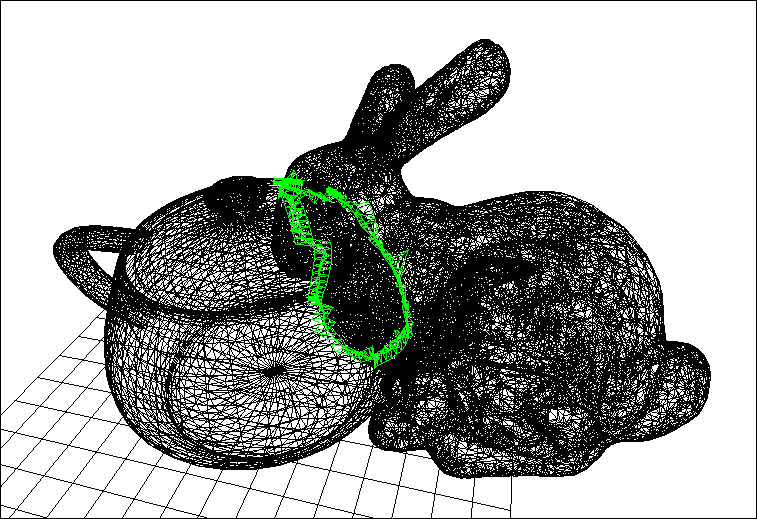
Figure 12. Détection de collisions entre deux surfaces. Les paires de triangles en intersection sont affichées en vert.
Dépose
Déposez le fichier TD789.java, qui comporte maintenant la fonction complétée intersectionSurfaceSurface(...).
Continuer?
Voulez-vous programmer quelques problèmes plus avancés? Continuer ici.
La conception de méthodes de recherche géométrique est un thème de recherche encore actif (objets complexes, objets déformables, détection de collisions continue, etc.), par exemple pour concevoir des méthodes de qualité utilisables dans les jeux vidéo, dans les logiciels de conception assistée par ordinateur, de simulation de dynamique moléculaire, etc. Ces TDs n'ont fait qu'aborder la question (tout en vous donnant une solide introduction au problème et aux méthodes employées). Si ce sujet vous intéresse, vous trouverez facilement plus d'informations en traînant sur Google.
Stéphane Redon - 2005-2012 - stephane.redon@inria.fr - http://nano-d.inrialpes.fr/~redon