| Votre opinion sur le cours de ce matin : | Votre opinion sur le TD de la semaine dernière : |
Dans ce TD, on cherche à résoudre un problème de combinatoire (parties 1 et 3) et pour y parvenir dans un temps raisonnable on construit une structure de table de hachage (parties 2 et 4). Si le temps le permet, on fera aussi du tirage aléatoire de murs de briques (partie 5).
On cherche à construire un mur à partir de briques horizontales de taille 2x1 et 3x1. Un mur est correctement construit si la jointure verticale entre deux briques ne se trouve jamais immédiatement au-dessus d'une autre jointure verticale. Ainsi le mur suivant est correctement construit :
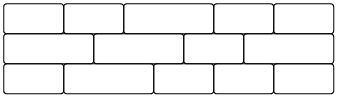
En revanche, celui-ci ne l'est pas (le problème est signalé en rouge) :
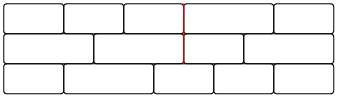
L'objectif du TD est de compter le nombre de façons différentes de construire correctement un mur de largeur 30 et de hauteur 10.
Pour dénombrer les murs, on va représenter les rangées de briques de la manière suivante. Une rangée de largeur n sera représentée par série de n+1 bits. Le i-ième bit indique si, au niveau de la i-ième unité de largeur, il y a ou non une jointure entre deux briques. Ainsi la rangée de briques de largeur 9

est représentée par les 10 bits 0010010100. On inclut les deux extrémités (ce qui explique les 10 bits pour une largeur 9), qui seront toujours des bits 0.
Maintenant, plutôt que d'utiliser un tableau de bits, il sera plus simple de voir une telle série de bits comme l'écriture binaire d'un entier. Ainsi, les 10 bits 0010010100 représentent en binaire l'entier 148 (les bits de poids faible sont à droite). Une rangée sera donc représentée par un int.
On utilisera les opérateurs de java sur les bits :
On remarquera que pour déterminer si une rangée de briques représentée par un entier r1 peut être posée sur une autre rangée représentée par un entier r2, il suffit de tester si r1 & r2 vaut zéro.
Téléchargez et importez le fichier squelette CountWall.java qui contient la classe
class CountWall {
LinkedList<Integer> allrows; // toutes les rangées possibles d'une largeur fixée
/** constructeur : mur de briques de largeur width */
CountWall(int width) {
// On prépare un tableau où la case i va contenir toutes les rangées de largeur i
ArrayList<LinkedList<Integer>> rows = new ArrayList<LinkedList<Integer>>(width + 1);
// À COMPLÉTER
this.allrows = rows.get(width);
}
/** count(row, height) : compte les murs de hauteur height dont la première rangée est row */
long count(Integer row, int height) {
return -1; // À MODIFIER
}
/** count(height) : compte tous les murs de hauteur height */
long count(int height) {
return -1; // À MODIFIER
}
/** fonctions tests et main */
...
}
Le champ allrows est la liste de toutes les rangées de briques possibles de largeur width. Comme une rangée est représentée par un entier, ce champ est donc naturellement de la classe LinkedList<Integer>.
Vous devez compléter le code du constructeur de la classe CountWall ci-dessus pour qu'il initialise allrows:
Pour cela, nous allons calculer la liste de toutes les rangées possibles de largeur i pour chaque valeur i entre 0 et width, que nous allons stocker dans un tableau rows de largeur width+1. En fait, nous utiliserons plutôt un ArrayList, qui est plus sécurisé qu'un tableau lorsque chaque case doit contenir un objet d'une classe générique (en l'occurrence, une liste de rangées, c'est-à dire un LinkedList<Integer>). L'accès au ième élément de rows se fait par rows.get(i). Après complétion du tableau rows, la liste allrows de toutes les rangées de largeur width sera donc rows.get(width).
On pourra tester en exécutant le Test1.java. On doit obtenir le résultat suivant (l'ordre des nombres sur la première ligne du résultat peut différer) :
[296, 168, 328, 148, 340, 292, 164] 3329
Déposez le fichier CountWall.java :
Pour dénombrer les murs, écrivez dans la classe CountWall une fonction récursive long count(int row, int height) qui détermine le nombre de murs dont la première rangée de briques est row et dont la hauteur est height. L'algorithme est le suivant :
On pourra tester cette méthode à l'aide du Test2.java dont l'exécution doit donner:
Liste des rangees de largeur 9 : [84, 148, 164, 168, 72] Nombre de murs de largeur 9, de hauteur 6, et commencant par la rangee 72 : 8
Déduisez-en une méthode long count(int height) qui calcule le nombre de murs de hauteur height.
On pourra la tester en exécutant le Test3.java qui doit fournir les résultats suivants:
Nombre de murs de largeur 9 et de hauteur 3: 8 Nombre de murs de largeur 12 et de hauteur 4: 52
Déposez le fichier CountWall.java :
Décommentez ensuite dans Test3.java la ligne
//test(30,10);
qui permet de calculer le nombre de murs de largeur 30 et de hauteur 10 et
relancez l'exécution.
Cela devrait afficher
Nombre de murs de largeur 9 et de hauteur 3: 8 Nombre de murs de largeur 12 et de hauteur 4: 52 Nombre de murs de largeur 30 et de hauteur 10: 56962090003246Que constatez-vous ?
Le programme est correct, mais avec une si mauvaise complexité qu'il ne termine pas en un temps raisonnable. Ceci est dû au fait qu'à cause des appels récursifs, count(row, height) est appelé de très nombreuses fois pour les mêmes valeurs row, height. Pour régler le problème, il suffit de mémoriser dans une table le triplet (row, height, count(row, height)) la première fois que l'on calcule count(row, height). Les fois suivantes, on ira directement chercher l'information dans la table sans recalculer la valeur. On pourrait utiliser la classe HashMap de Java pour réaliser une telle table. Cependant, l'idée est aujourd'hui de réaliser nous-mêmes une table de hachage.
On va écrire une structure de données qui associe à des paires d'entiers de type int une valeur de type long.
On utilise une classe Triple pour représenter les entrées de cette table, c'est-à-dire des triplets (x,y,result) où x et y sont deux entiers de type int et result un entier de type long. Dans la suite de l'énoncé, on appellera "entrée pour le couple (x,y)" tout triplet de la forme (x,y,result). Cette classe contient :
class Triple {
int x, y;
long result;
Triple(int x, int y, long result) {
this.x = x;
this.y = y;
this.result = result;
}
}
Téléchargez et importez le fichier Triple.java.
Une table de hachage n'est rien d'autre qu'un tableau de listes de triplets, où l'élément d'indice i contient les triplets pour lequels la valeur de hachage vaut i modulo la taille du tableau. On utilise la classe LinkedList pour représenter les listes et on choisit une valeur arbitraire (ici 5003) pour la taille du tableau. On a donc une classe Table de la forme suivante :
import java.util.LinkedList;
class Table {
final static int M = 5003;
LinkedList<Triple>[] buckets;
@SuppressWarnings("unchecked")
Table() {
this.buckets = new LinkedList[M]; // ne pas écrire <Triple> ici
}
}
Dans toute la partie 2, on va travailler uniquement dans cette classe Table.
Complétez le code du constructeur de la classe Table pour que chaque élément du tableau buckets soit bien initialisé avec une nouvelle LinkedList.
Dans la classe Table, écrivez une méthode int hashCode(int x, int y) qui calcule une valeur de hachage arbitraire pour la paire (x,y). Toute formule arithmétique impliquant à la fois x et y fera l'affaire.
Dans la classe Table, écrivez une méthode int bucket(int x, int y) qui renvoie la valeur de hashCode(x,y) modulo M. Attention : le résultat de l'opérateur modulo de Java (%) sur des entiers négatifs peut être lui-même négatif. On veillera donc ici à garantir un résultat entre 0 (inclus) et M (exclus).
Dans la classe Table, ajoutez une méthode void add(int x, int y, long r) pour ajouter une entrée dans la table de hachage. On ne cherchera pas à vérifier si l'entrée existe déjà ; on se contentera d'ajouter systématiquement à la liste.
Dans la classe Table, ajoutez une méthode Triple find(int x, int y) qui recherche dans la table une entrée pour le couple (x,y). S'il existe dans la table une telle entrée, la première entrée trouvée pour (x,y) est renvoyée. Sinon, la valeur null est renvoyée.
On pourra tester avec le Test4.java dont le résultat doit être le suivant :
null 3 null 42
Déposez le fichier Table.java :
On revient sur le problème de combinatoire initial, et on travaille donc de nouveau dans la classe CountWall.
Ajoutez un champ memo de type Table dans la classe CountWall et son initialisation dans le constructeur.
Modifiez votre méthode long count(int row, int height) de la classe CountWall en utilisant le champ memo pour mémoriser les calculs déjà effectués. L'algorithme est maintenant le suivant :
Exécutez de nouveau Test3.java en calculant enfin le nombre de murs de largeur 30 et de hauteur 10 (ce qui ne doit pas prendre plus de quelques secondes). On doit obtenir le résultat suivant :
Nombre de murs de largeur 30 et de hauteur 10: 56962090003246
Déposez le fichier CountWall.java :
Créez une classe CountWall2.java à partir de CountWall.java en modifiant votre code pour utiliser la classe HashMap de la bibliothèque standard de Java à la place de votre classe Table.
Indication : les clés étant des paires d'entiers, il vous faudra introduire une classe Pair pour les représenter, afin de pouvoir utiliser l'instance HashMap<Pair, Long>. Cette classe Pair devra redéfinir ses méthodes public boolean equals(Object o) et public int hashCode().
Vous pourrez tester votre code à l'aide du fichier Test3Bis.java.Déposez le fichier CountWall.java :
Pour finir ce TD, on va maintenant écrire un algorithme pour tirer aléatoirement un mur de briques de largeur width et de hauteur height uniformément parmi tous les murs ayant cette largeur et cette hauteur. On voudra ensuite l'afficher pour se faire une idée du résultat.
On utilise pour cela une classe RandomWall, fournie dans le fichier squelette RandomWall.java, avec les champs :
Notez que l'on n'a pas besoin de retenir la hauteur du mur puisqu'on peut l'obtenir avec rows.size().
Complétez la méthode récursive void fill(int row, int height) qui prend en arguments une rangée int row et une hauteur int height, et construit aléatoirement un mur de largeur width, de hauteur height, et dont la première rangée est row, et stocke les rangées de ce mur dans rows. Pour cela, il faudra
En utilisant cette méthode fill, complétez le constructeur RandomWall(int width, int height) qui construit un mur aléatoire de largeur width et de hauteur height, uniformément parmi tous les murs ayant cette largeur et cette hauteur.
Complétez la méthode public String toString() qui affiche un mur en plaçant une barre | à chaque jointure verticale entre deux briques, et des barres _ pour séparer les briques.
Testez enfin votre programme à l'aide du Test5.java On doit obtenir par exemple :
java RandomWall 30 10 _______________________________________________________________________________________ |____|________|________|_____|_____|_____|_____|_____|________|_____|________|_____|____| |_______|________|________|_____|_____|_____|_____|________|_____|________|_____|_______| |____|_____|________|________|_____|_____|_____|________|_____|_____|________|_____|____| |_______|________|_____|________|_____|_____|_____|________|_____|________|_____|_______| |____|_____|________|_____|________|_____|_____|_____|________|________|_____|_____|____| |_______|________|_____|_____|________|_____|_____|_____|________|________|_____|_______| |____|_____|________|_____|_____|________|_____|_____|________|_____|________|_____|____| |_______|_____|________|_____|_____|________|_____|_____|________|_____|________|_______| |____|_____|_____|________|_____|________|_____|_____|________|_____|________|_____|____| |_______|_____|_____|________|_____|________|_____|________|_____|________|_____|_______|
Évidemment, le résultat est aléatoire, donc vous devez juste obtenir quelque chose qui ressemble à ça !
Déposez le fichier RandomWall.java :
Si vous avez aimé ce problème, vous adorerez le Projet Euler.
Voici une solution possible : solution.zip. Les fichiers individuels sont là :