

| Votre opinion sur le cours de ce lundi : | Votre opinion sur le TD de la semaine dernière : |
Le compte est bon est une épreuve du jeu télévisé Des chiffres et des lettres qui consiste à obtenir un nombre cible à partir de nombre tirés au hasard et des quatre opérations élémentaires.
Dans ce TD, on se propose d'écrire un programme qui calcule tous les nombres positifs qui peuvent être obtenus à partir des nombres de départ. On va pour cela écrire une classe pour représenter des ensembles d'entiers et écrire une méthode qui prend en argument un ensemble de nombres de départ et renvoie l'ensemble des nombres que l'on peut construire.Les ensembles vont être représentés par des arbres binaires de recherche. Comme dans le cours, on commence par écrire une classe BST avec des méthodes statiques, où null représente l'arbre vide.
Les fichiers à télécharger avant de commencer ce TD:
On vous fournit une classe BST.java à compléter. Cette classe contient déjà :
BST a = new BST(); // ... a = BST.insert(a,x);
Dans la classe BST, écrire une méthode static BST merge(BST a, BST b) qui fusionne les arbres a et b, en supposant que tous les éléments de a sont plus petits que les éléments de b. On s'inspirera de la figure suivante, où m est la valeur minimale de l'arbre b :
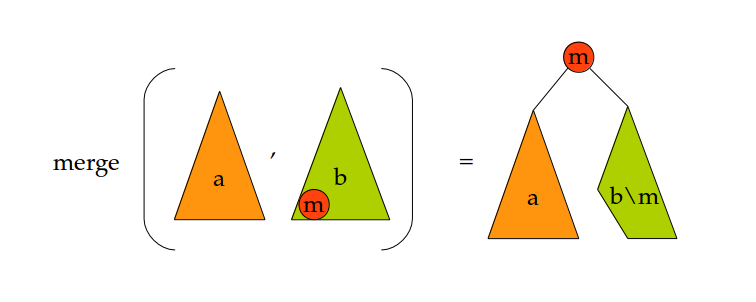
Déposez le fichier BST.java :
Dans la classe BST, écrire une méthode récursive private static void toList(LinkedList<Integer> l, BST s) qui ajoute à la fin de la liste chaînée l les éléments de s dans l'ordre croissant. On pourra s'inspirer des explications données en amphi à ce sujet.
En déduire une méthode static LinkedList<Integer> toList(BST s) qui renvoie une liste chaînée contenant les éléments de l'arbre s dans l'ordre croissant.
Utiliser la classe Test12.java pour valider votre code ; l'exécution de cette dernière doit produire à l'écran :
[Testing BST.toList] [Test #0 (size: 0)] OK [Test #1 (size: 1)] OK [Test #2 (size: 2)] OK ... [9 tests passed, 0 tests failed]Finalement, vérifiez bien que l'arbre (qui sera visible dans une fenêtre) est bien cohérent.
Déposez le fichier BST.java :
Nous souhaitons calculer toutes les partitions possibles d'un ensemble d'entiers (représenté par un ABR) en deux ensembles complémentaires (représentés par un couple d'ABR). En voici un exemple :
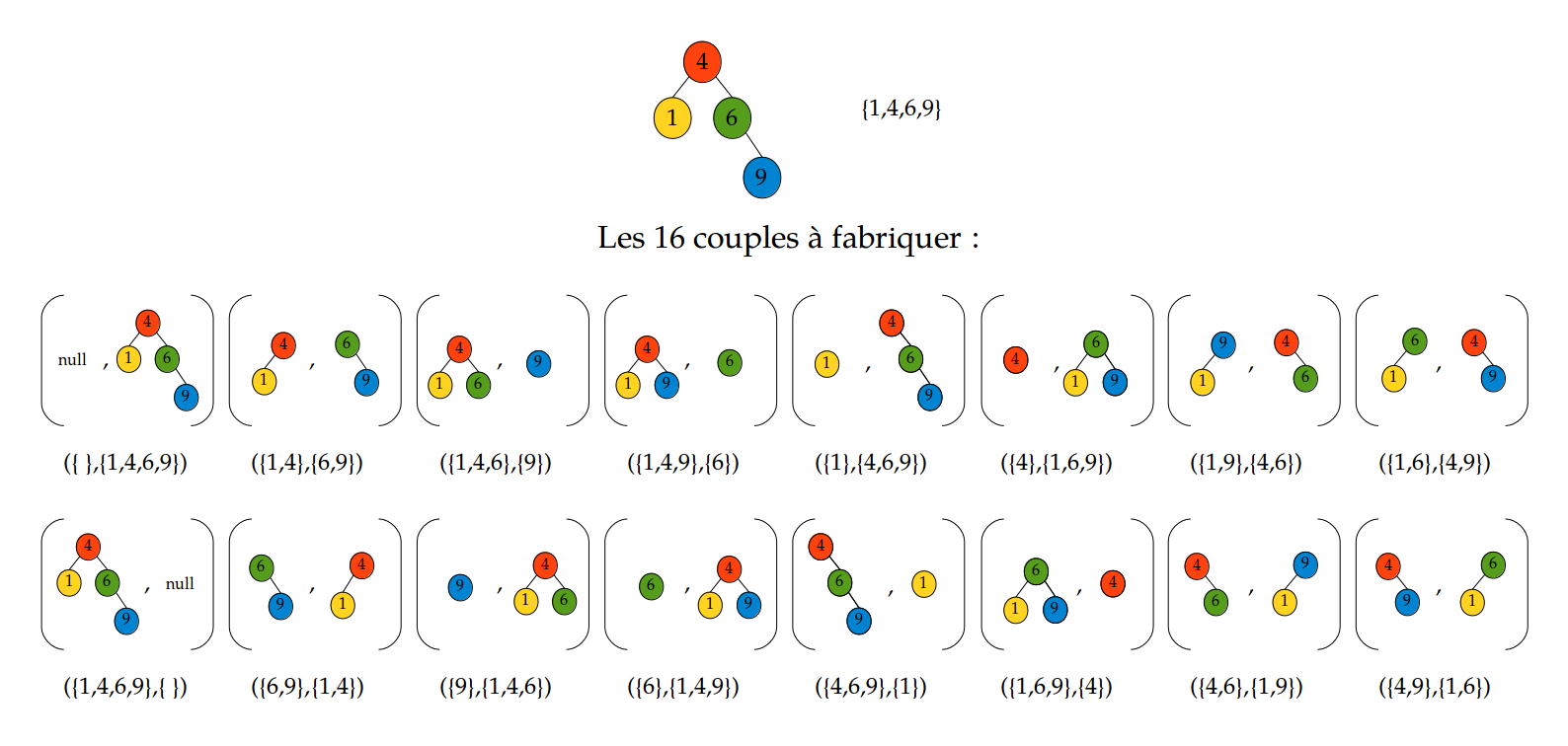
La structure des ABR n'est pas importante ici ; seuls les éléments contenus dans les ABR sont importants. Autrement dit, on doit obtenir tous les couples de sous-ensembles complémentaires possibles mais pour un sous-ensemble particulier, par exemple {4,6,9}, peu importe la structure de l'ABR qui le représente.
On note que les couples (a,b) et (b,a) doivent tous deux être présents dans la liste des décompositions possibles. Sur la figure ci-dessus, on trouve bien le couple ({1,4},{6,9}) et le couple ({6,9},{1,4}).
Pour calculer toutes les décompositions possibles, nous allons procéder récursivement. Si l'on connaît toutes les décompositions possibles pour les sous-arbres gauche et droit, il suffit de les combiner de toutes les manières possibles, en ajoutant ou non la racine, pour obtenir toutes les décompositions possibles de l'arbre initial. Examinons le schéma suivant :
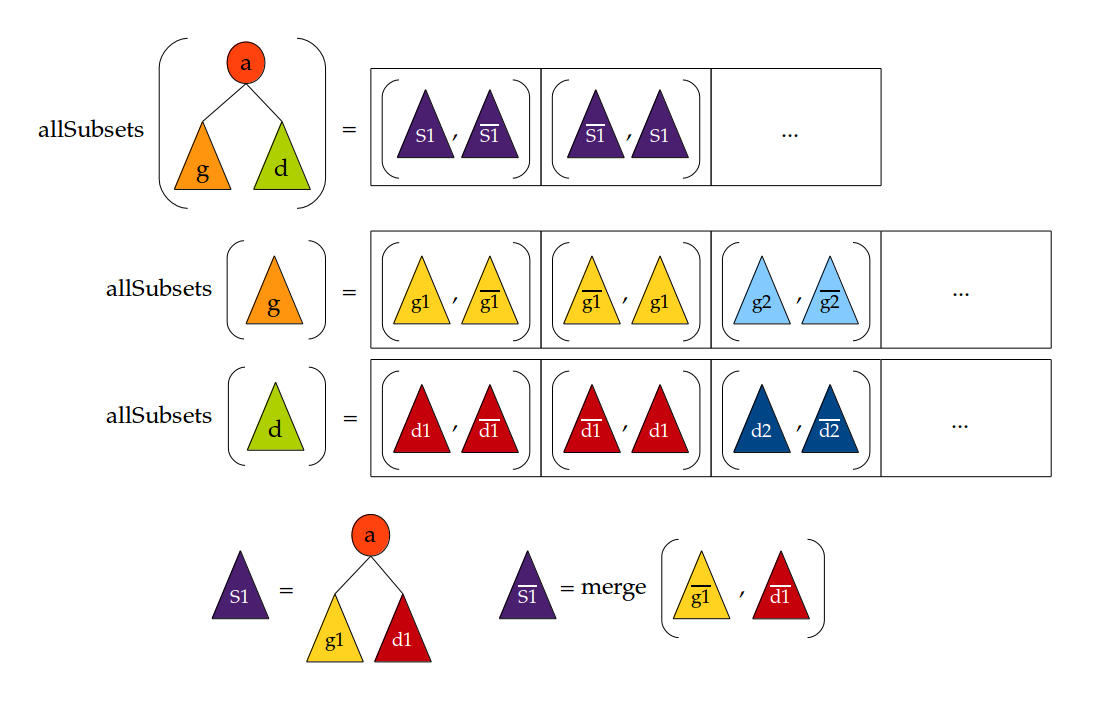
Soient g et d les sous-arbres gauche et droit de l'arbre initial et soit a sa racine. Soient (g1,g1) une décomposition possible du sous-arbre gauche g et (d1,d1) une décomposition possible du sous-arbre droit d. À partir de g1, g1, d1 et d1, on peut former les deux décompositions (S1,S1) (S1,S1) telles qu'illustrées sur le schéma. Sur la figure, nous avons représenté uniquement les décompositions obtenues à partir des décompositions (g1,g1) pour le sous-arbre g et (d1,d1) pour le sous-arbre d. Il faudra bien sûr le faire pour tous les couples de décompositions possibles. On peut se convaincre qu'on obtient bien ainsi toutes les décompositions de l'arbre initial.
On a fourni la classe Pair<X> pour représenter un couple de valeurs du type X. Pour construire un couple d'arbres (f, s), on utilisera le constructeur new Pair<BST>(f, s) ; les deux éléments d'un couple p sont accessibles via les champs p.first et p.second.
Dans la classe BST.java, écrire une méthode static Vector<Pair<BST>> allSubsets(BST a) qui renvoie un vecteur de couples d'ABR représentant l'ensemble des décompositions possibles de l'arbre a.
Utiliser la classe Test13.java pour valider votre code ; l'exécution de cette dernière doit produire à l'écran :
[Test #0 (size: 0 entries)] BST = [] -> 1 subsets ([],[]) [Test #1 (size: 1 entries)] BST = [5] -> 2 subsets ([5],[]) ([],[5]) [Test #2 (size: 2 entries)] BST = [2, 5] -> 4 subsets ([2, 5],[]) ([],[2, 5]) ([5],[2]) ([2],[5]) [Test #3 (size: 3 entries)] BST = [2, 5, 8] -> 8 subsets ([2, 5, 8],[]) ([],[2, 5, 8]) ([2, 5],[8]) ([8],[2, 5]) ([5, 8],[2]) ([2],[5, 8]) ([5],[2, 8]) ([2, 8],[5]) [Test A (check BST in graphics window)]
Déposez le fichier BST.java :
Nous allons maintenant écrire une classe LeCompteEstBon dans laquelle nous calculons l'ensemble des résultats possibles à partir d'un ensemble d'entiers. Chaque entier de l'ensemble de départ doit être utilisé au plus une fois. Seuls les résultats strictement positifs sont autorisés.
Tout d'abord, créer une classe LeCompteEstBon (en respectant scrupuleusement la casse dans le nom de la classe) avec un champ privé seeds de type Set. Il s'agit des entiers de départ.
Définir un constructeur public LeCompteEstBon(int[] numbers) qui initialise le champ seeds en y mettant les nombres contenus dans le tableau numbers.
Nous passons à la phase de calcul des résultats. Pour ce faire, définissez une méthode récursive private Set getResults(Set s) qui renvoie l'ensemble des résultats possibles à partir de l'ensemble s. Cette dernière procédera récursivement : dans le cas où l'ensemble est vide ou bien réduit à un singleton, l'ensemble de retour est trivial à calculer. Dans les autres cas, il faudra examiner toutes les décompositions possibles de s en deux sous-ensembles complémentaires x et x. Si x ou x est vide, il n'y a rien à faire. Sinon, on note respectivement R et R les ensembles issus des appels récursifs de la méthode getResults sur x et sur x. Alors, pour chaque valeur u contenue dans R et pour chaque valeur v contenue dans R, il faudra ajouter à l'ensemble résultat les valeurs u, u+v, u-v (si cette valeur est strictement positive), u*v et u/v (si la division est entière).
Dans la classe LeCompteEstBon, écrire cette méthode private Set getResults(Set s), ainsi qu'une méthode public Set getResults() qui renvoie l'ensemble des résultats possibles pour l'ensemble seeds.
Utiliser la classe Test21.java pour valider votre code ; l'exécution de cette dernière doit produire à l'écran :
[Testing LeCompteEstBon getResults]
[Test #0 (size: 0 seeds)]
Seeds = {}
Results = #0[]
[Test #1 (size: 1 seeds)]
Seeds = {4}
Results = #1[4]
[Test #2 (size: 2 seeds)]
Seeds = {4, 1}
Results = #4[1, 3, 4, 5]
[Test #3 (size: 3 seeds)]
Seeds = {4, 1, 5}
Results = #16[1, 2, 3, 4, 5, 6, 8, 9, 10, 15, 16, 19, 20, 21, 24, 25]
Déposez le fichier LeCompteEstBon.java :
Comme nous l'avons vu dans le TD2, la mémoïsation est une excellente solution dans le cas où un calcul récursif refait un grand nombre de fois les mêmes calculs. Or, c'est le cas ici pour la méthode getResults.
Ajouter un nouveau champ private HashMap<Set,Set> results dans la classe LeCompteEstBon. Initialiser ce champ dans le constructeur. Cette table va mémoïser les ensembles calculés par la méthode getResults. Plus précisément, nous stockerons dans results des couples (s, getResults(s)), l'ensemble s étant la clé et getResults(s) la valeur associée.
Comme expliqué la semaine dernière, l'utilisation d'une table de hachage nécessite que les méthodes equals et hashCode de la classe des clés soient correctes et cohérentes. Il nous faut donc ici redéfinir ces méthodes pour la classe Set.
Pour cela, nous pourrions tout simplement passer par les listes produites par la méthode toList. En effet, si deux ensembles A et B sont représentés par des ABR différents mais contiennent les mêmes valeurs, alors les listes produites par la méthode toList seront identiques. Dès lors, il suffit de calculer hashCode et equals sur les listes. C'est cependant une façon inefficace de procéder, car on construit des listes inutilement : dans le cas de hashCode, un simple parcours de l'arbre suffit ; dans le cas de equals, il est regrettable de construire les deux listes intégralement pour découvrir qu'elles diffèrent rapidement. Nous vous proposons ici une manière plus élégante de procéder.
Écrire une méthode static int computeHashCode(BST s) dans la classe BST, puis une méthode public int hashCode() dans la classe Set.
Deux ABR qui contiennent les mêmes éléments doivent avoir la même valeur de hashCode, alors qu'ils peuvent avoir des structures différentes. Comme pour la méthode toList, nous vous conseillons de passer par une méthode intermédiaire static int computeHashCode(BST s, int hash), où le paramètre hash joue le rôle d'accumulateur. Cette méthode doit construire sa valeur de retour en faisant un parcours infixe de l'arbre s.
Utiliser la classe Test31.java pour valider votre code ; l'exécution de cette dernière doit produire à l'écran :
[Testing Set hashCode] [Test #0 (size 0)] OK [Test #1 (size 1)] OK [Test #2 (size 2)] OK ... [20 tests passed, 0 tests failed]
Déposez les fichiers BST.java et Set.java :
Le but est maintenant d'écrire une méthode static boolean areEqual(BST p, BST q) dans la classe BST qui détermine si deux ABR p et q contiennent les mêmes éléments.
L'idée consiste à énumérer simultanément les éléments de deux arbres dans l'ordre croissant. Ainsi nous serons en mesure, le cas échéant, de déterminer que deux arbres sont différents sans avoir à les parcourir entièrement. Pour ce faire, nous allons introduire une classe Enum qui jouera ce rôle d'énumérateur. Cette classe contient :
Créer cette classe Enum avec ses champs et son constructeur.
Un objet de type Enum représente la branche gauche d'un ABR, de bas en haut, comme une liste chaînée où chaque élément est accompagné de son sous-arbre droit. Voici deux ABR et leurs branches gauches correspondantes :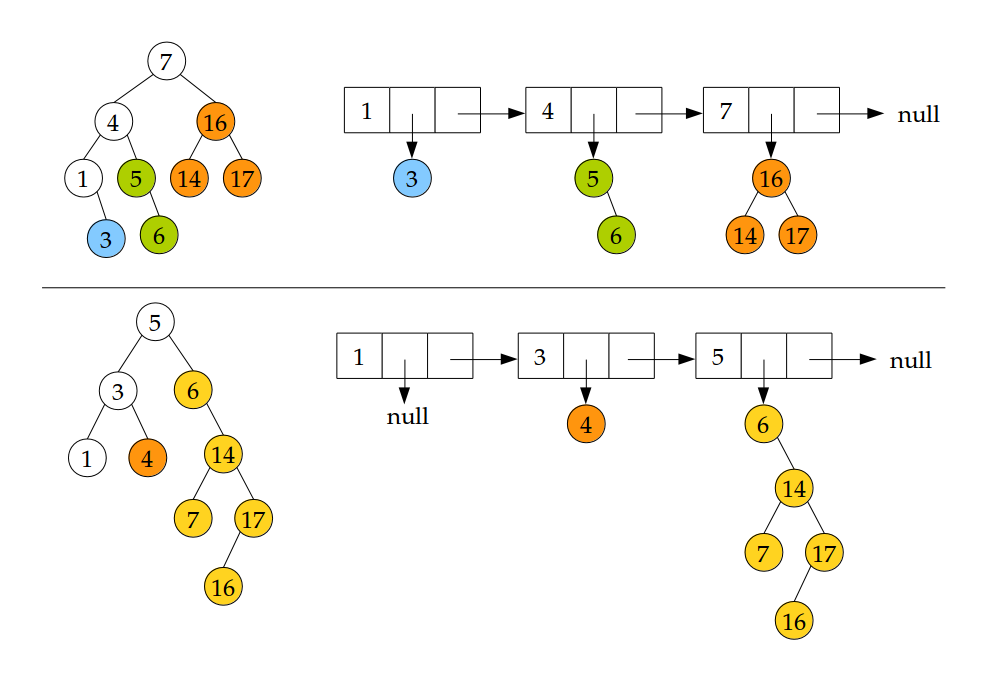
La construction d'une énumération à partir d'un ABR se fait à l'aide d'une méthode récursive static Enum build(BST a, Enum next). Cette méthode construit la branche gauche de a, de bas en haut, et la concatène à la liste next. Voici un schéma illustrant le comportement de cette méthode :
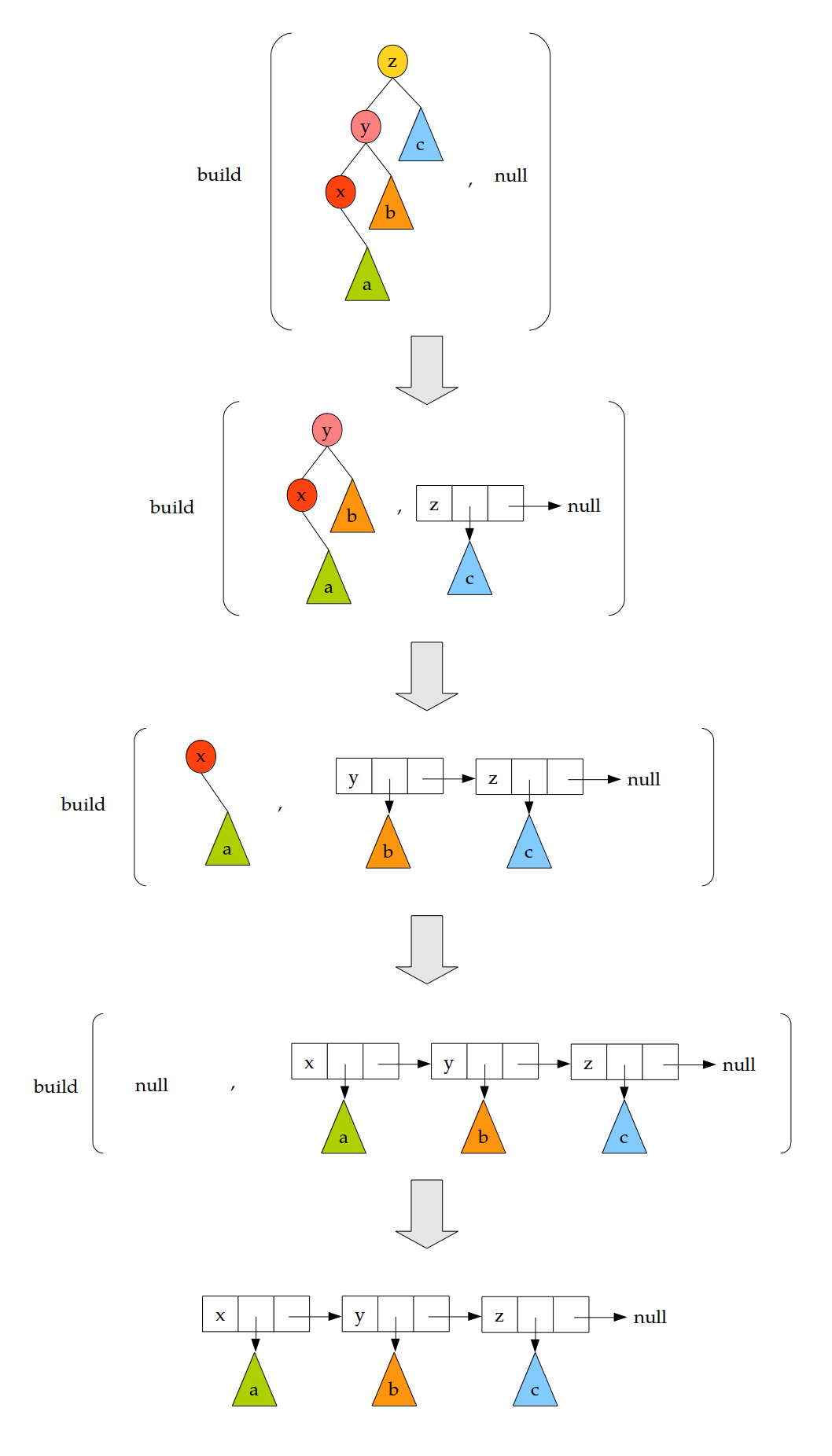
Dans la classe Enum, écrire la méthode static Enum build(BST a, Enum next).
Il faut maintenant décider si deux énumérations représentent le même ensemble d'éléments. Pour ce faire, écrire une méthode static boolean areEqual(Enum x, Enum y). Les cas où x et/ou y sont vides sont laissés à vos soins. Dans les autres cas, il se peut que deux énumérations soient différentes dans leur structure, mais qu'elles contiennent les mêmes éléments. Néanmoins, on peut remarquer qu'elles doivent avoir le même premier élément. Et il est également simple de retirer le plus petit élément d'une énumération, en se resservant de la méthode build. Vous avez alors tous les ingrédients pour écrire la méthode static boolean areEqual(Enum x, Enum y).
En déduire la méthode static boolean areEqual(BST p, BST q) dans la classe BST. Une ligne doit suffire.
Enfin, encapsuler la méthode areEqual de BST dans une méthode public boolean equals(Object o) dans la classe Set.
Utiliser la classe Test32.java pour valider votre code ; l'exécution de cette dernière doit produire à l'écran :
[Testing BST.areEqual] [Test #0.1 (size 0,0)] OK [Test #0.2 (size 0,1)] OK [Test #1.1 (size 1,1)] OK ... [40 tests passed, 0 tests failed]
Déposez les fichiers BST.java, Enum.java et Set.java :
Avant de modifier votre classe LeCompteEstBon, exécuter la classe Test33.java pour voir le temps de calcul sans mémoïsation :
[Testing LeCompteEstBon getResults] [Test #0 (size: 0 seeds, 0 results)] OK time = 2.0ms [Test #1 (size: 1 seeds, 1 results)] OK time = 1.0ms [Test #2 (size: 2 seeds, 4 results)] OK time = 0.0ms [Test #3 (size: 3 seeds, 16 results)] OK time = 0.0ms [Test #4 (size: 4 seeds, 64 results)] OK time = 6.0ms [Test #5 (size: 5 seeds, 189 results)] OK time = 86.0ms [Test #6 (size: 6 seeds, 987 results)] OK time = 361.0ms [Test #7 (size: 7 seeds, 6032 results)] OK time = 1727.0ms [Test #8 (size: 8 seeds, 32366 results)] OK time = 53618.0ms [9 tests passed, 0 failed] Total time: 55802.0 ms
Modifier maintenant la méthode getResults(Set s) dans la classe LeCompteEstBon afin d'utiliser la mémoïsation.
Exécuter à nouveau la classe Test33.java afin de voir le temps de calcul avec mémoïsation :
[Testing LeCompteEstBon getResults] [Test #0 (size: 0 seeds, 0 results)] OK time = 0.0ms [Test #1 (size: 1 seeds, 1 results)] OK time = 0.0ms [Test #2 (size: 2 seeds, 4 results)] OK time = 0.0ms [Test #3 (size: 3 seeds, 16 results)] OK time = 1.0ms [Test #4 (size: 4 seeds, 64 results)] OK time = 3.0ms [Test #5 (size: 5 seeds, 189 results)] OK time = 18.0ms [Test #6 (size: 6 seeds, 987 results)] OK time = 67.0ms [Test #7 (size: 7 seeds, 6032 results)] OK time = 385.0ms [Test #8 (size: 8 seeds, 32366 results)] OK time = 15518.0ms [9 tests passed, 0 failed] Total time: 15996.0 ms
Déposez le fichier LeCompteEstBon.java :
Voici une solution possible : solution.zip.