TD 4 - Arbres binaires de recherche
Quelle structure utiliser pour stocker des données ?
Comme on peut bien l'imaginer, la réponse à cette question n'est
pas unique, et dépend de plusieurs paramètres, parmi lesquels
:
- n, le nombre d'éléments stockés,
- le type d'opérations que l'on souhaite pouvoir effectuer,
que ces opérations visent à éditer la structure (comme l'ajout
d'éléments) ou pas (comme rechercher un élément)
- le type des éléments (entiers, flottants, String,...), et
les méthodes disponibles pour ces éléments (fonction de
hachage,...)
Après avoir vu les listes, les tableaux, les tables de hachage,
nous voyons aujourd'hui une structure de données qui exploite un
ordre total entre les éléments : les arbres binaires de recherche.
Concrètement, nous allons utiliser ces arbres pour implanter des
ensembles d'entiers (munis de l'ordre habituel), l'ajout
d'éléments, l'union de deux ensembles, ainsi que les tests
d'inclusion et d'égalité entre ensembles...
0. Introduction
Récupération des fichiers
Voici certains fichiers dont vous aurez besoin dans ce TD (contenus
dans le fichier sources.zip à
télécharger et décompresser) :
| TreeNode.java |
classe représentant le sommet
d'un arbre binaire de recherche (à compléter)
|
|
Enum.java
|
classe permettant de tester l'égalité entre
deux arbres binaires (à compléter) |
|
Pair.java
|
classe permettant de renvoyer des paires d'objets (rien à coder) |
|
1. Opérations élémentaires sur les arbres binaires de recherche:
(création, mise à jour, et requêtes)
1.1 La classe TreeNode
Pour représenter en Java
un ensemble ordonné comme un arbre binaire de recherche, nous
allons utiliser la classe TreeNode, qui représente un
noeud de l'arbre, avec les pointeurs vers ses deux fils.
public class TreeNode {
final int value;
final TreeNode left, right;
public TreeNode(TreeNode left, int value, TreeNode right) {
throw new Error("A completer: exo 1");
}
public TreeNode(int value) {
throw new Error("A completer: exo 1");
}
static boolean contains(TreeNode b, int x) {
throw new Error("A completer: exo 1");
}
...
...
...
}
Dans ce TD, et dans ce TD seulement, l'arbre vide sera représenté par le pointeur null.
Aujourd'hui on vous demande de compléter les méthodes de la classe TreeNode,
qui contient :
- un champ final int value, qui contient la valeur
stockée dans le sommet ;
- deux champs final TreeNode left,
right contenant les références vers les (sommets
racines des) sous-arbres gauche et droit respectivement.
Remarques :
On souhaite représenter les arbres de manière persistante : les
champs ci-dessus sont déclarés comme final,
donc ils ne peuvent être affectés qu'une seule fois (lors de la
création avec les constructeurs de la classe TreeNode). Si
un sommet est une feuille
(pas de fils), alors les champs right et left
sont null.
Modifiez le fichier TreeNode.java en complétant les
méthodes suivantes :
- le constructeur TreeNode(int value) qui construit une
feuille (pas de fils) contenant la valeur value ;
- le constructeur TreeNode(TreeNode left, int value,
TreeNode right) qui construit un sommet interne,
avec sous-arbres gauche et droit donnés, et contenant la valeur
value ;
- la méthode contains(TreeNode b, int x) qui
renvoie true si l'arbre b contient la
valeur x;
- la méthode getMin(TreeNode b) qui renvoie la valeur
minimale contenue dans l'ensemble. On supposera que l'arbre
passé en argument TreeNode b n'est jamais le
pointeur null (c'est-à-dire que l'ensemble représenté
a au moins un élément) : plus exactement, nous n'imposons
aucune spécification sur le comportement de la méthode si
l'argument est le pointeur null.
Remarque: la valeur est à rechercher
dans la branche la plus à gauche.
- la méthode add(TreeNode b,int e) qui ajoute un nouvel élément à
l'arbre (de manière à ce que l'invariant des arbres binaires de
recherche soit maintenu). Remarque: on évitera de
stocker plusieurs copies, chaque valeur étant ajoutée une seule
fois.
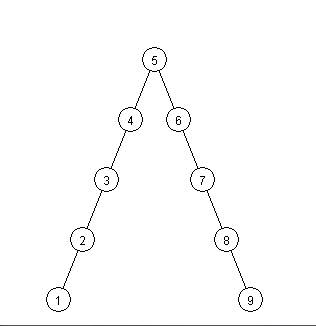
Pour tester votre code, utilisez la fonction test1() de la classe TestBSTSet.
Vous devez obtenir le résultat suivant :
S1=[ 1 2 3 4 5 6 7 8 9]
true
true
true
false
false
min=1
|
|
Déposez le fichier TreeNode.java :
2. Opérations ensemblistes sur un arbre binaire de recherche
2.1 Tester si un ensemble est sous-ensemble d'un autre
On va maintenant illustrer un algorithme (récursif) permettant
de tester si l'ensemble des éléments d'un arbre binaire de
recherche est contenu dans un autre arbre.
Appelons A et B
les deux arbres en entrée ; soit a la valeur
de la racine de A, et Ag,
Ad ses deux sous-arbres gauche et
droit (de manière similaire on notera b la
valeur de la racine de B):
- si A est vide, alors A est
sous ensemble de B;
- sinon, si B est vide, la fonction doit
renvoyer faux;
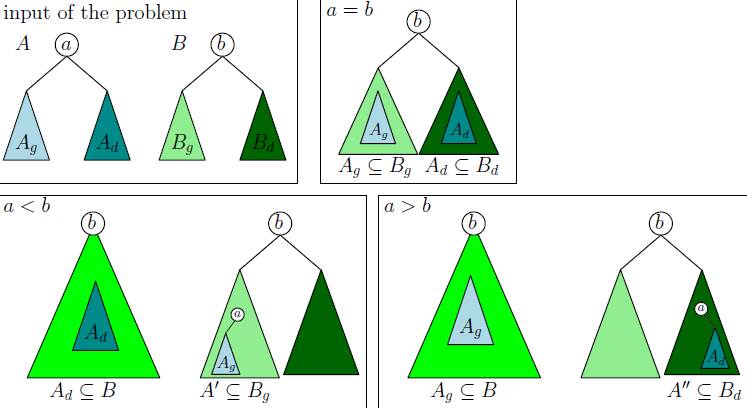
- sinon, on distingue 3 cas, selon les valeurs de a
et b. La figure à droite illustre, dans
les 3 cas, les conditions qui doivent être vérifiées
pour que A soit sous-ensemble de B.
|
|
Complétez
- la fonction boolean subset(TreeNode s1,
TreeNode s2) qui teste si s1
est un sous-ensemble de s2.
Pour tester votre code, utilisez la fonction
test2()
(classe
TestBSTSet).
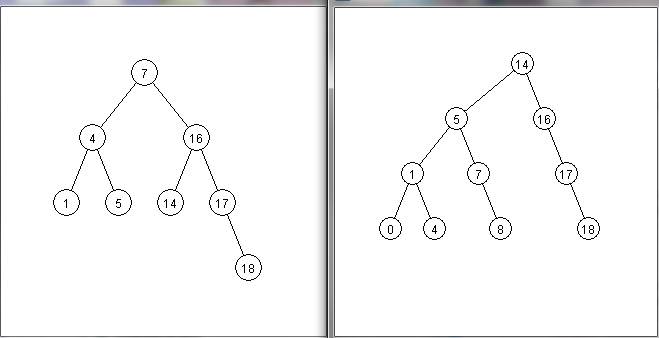
Testing subset
b1=[ 1 4 5 7 14 16 17 18]
b2=[ 0 1 4 5 7 8 14 16 17 18]
b1<=b2? true
b2<=b1? false
|
|
Déposez le fichier
TreeNode.java :
2.2 Union de deux arbres de recherche
On considère maintenant le problème consistant
à calculer l'union de deux ensembles (représentés sous
forme d'arbres binaires de recherche).
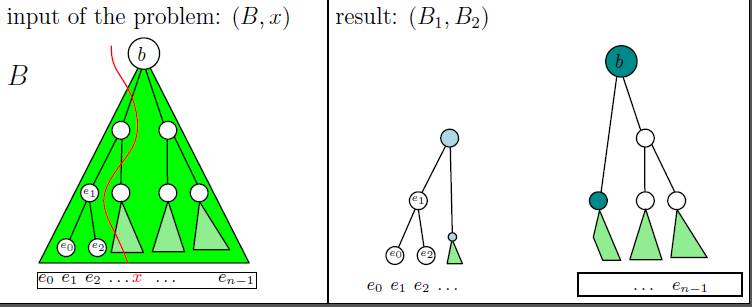
Le procédé est récursif, et fait intervenir une fonction
auxiliaire (appelée split) qui décompose les
éléments stockés dans l'arbre en deux parties :
la première correspond aux éléments strictement
inférieurs à une valeur donnée x ;
la deuxième partie contient les éléments
strictement supérieurs à cette valeur.
Ces parties seront renvoyées sous la forme d'une paire
de deux arbres, donc un objet de la
classe Pair. Notez que
si x appartient à l'arbre, il n'appartient à
aucun des deux arbres renvoyés
par split.
|
|
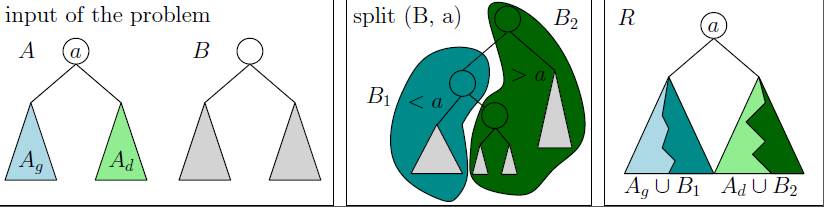
Le procédé pour l'union (récursif)
est donné ci-dessous. Appelons A et B
les deux arbres en entrée ; soit a la valeur de
la racine de A, et Ag,
Ad ses deux sous-arbres gauche et
droit :
- si l'un des deux arbres est vide, on termine en
renvoyant l'autre ;
- sinon
- on décompose l'ensemble B (autour de la
valeur a) : on obtient ainsi deux arbres B1
et B2.
- récursivement on crée deux sous-arbres G:=(Ag
union B1) et D:= (Ad
union B2) ;
- on renvoie comme résultat l'arbre R,
ayant comme valeur racine a, et dont le
sous-arbre gauche et droit sont respectivement G
et D.
|
|
Il vous reste donc à compléter
- la fonction auxiliaire Pair split(int x, TreeNode
s) qui renvoie deux nouveaux arbres, contenant
respectivement les éléments qui sont plus petits et plus
grands que la valeur x. Notez également que la
méthode union n'a pas besoin d'etre appelee pour construire
la paire.
- la fonction TreeNode
union(TreeNode s1, TreeNode s2)
qui décompose un arbre binaire de recherche (suivant le procédé
décrit ci-dessus) ;
Pour tester votre code, utilisez la fonction
test3() de
la classe
TestBSTSet. Vous devez obtenir le résultat
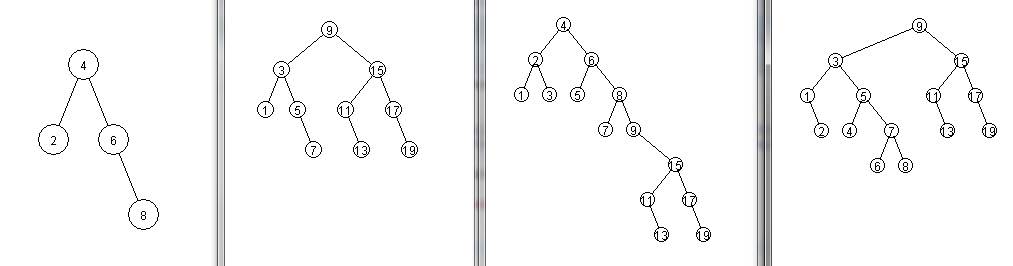
ci-dessous. Les deux arbres
u1
et
u2 (images sur la droite) représentent le même
ensemble, obtenu comme union des deux arbres
b1
et
b2 (figures de droite)
Testing union
b1: [ 2 4 6 8]
b2: [ 1 3 5 7 9 11 13 15 17 19]
u1:=b1 U b2 = [ 1 2 3 4 5 6 7 8 9 11 13 15 17 19]
u2:=b2 U b1 = [ 1 2 3 4 5 6 7 8 9 11 13 15 17 19]
|
|
Déposez le fichier
TreeNode.java :
2.3 Test d'égalité
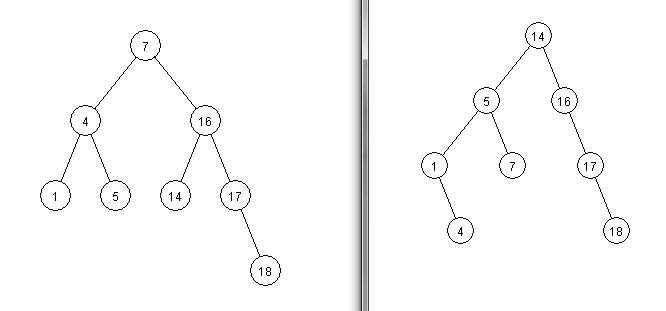
| Comme vous pouvez
l'imaginer, deux arbres binaires de recherche peuvent
représenter le même ensemble mais avoir différentes
structures. Un exemple est fourni par les deux arbres
(à droite) représentant les mêmes éléments (les
éléments sont bien sûr listés dans le même ordre,
selon le parcours infixe).
Dans cet exercice, on cherche à écrire un algorithme
qui teste si deux arbres binaires de recherche
représentent le même ensemble. On pourrait
convertir les deux arbres en listes triées d'entiers
et comparer ces dernières, mais ces conversions
nécessitent de parcourir entièrement les deux
arbres, ce qu'il est dommage de faire si par exemple
les deux arbres diffèrent dès leurs plus petits
éléments.
L'idée est de procéder paresseusement : au lieu d'aplatir entièrement un
arbre en une liste d'entiers, nous allons le convertir en une
liste dont chaque maillon contient un entier et un
arbre. Cette liste a la même longueur que la branche la plus à
gauche de l'arbre de départ et chaque maillon correspond à un
noeud de cette branche : l'entier du maillon est la valeur sur
le noeud, et l'arbre dans le maillon est le fils droit du
noeud.
Le premier des deux arbres ci-contre sera donc converti en
une liste dont la tête contient l'entier 1 et
l'arbre null, dont le deuxième maillon contient
l'entier 4 et l'arbre réduit à la feuille 5, et le troisième
maillon contient l'entier 7 et l'arbre de racine 16
(inchangé).
|
|
Une telle liste sera un objet de la classe
Enum (voir
ci-dessous).
Vous devez compléter d'abord :
- la méthode Enum build(TreeNode t, Enum
acc) qui construit la liste
représentant (comme décrit ci-dessus)
l'arbre t, en la concaténant à la
liste acc qui vient derrière. On écrira
une méthode récursive, acc jouant le
rôle d'un accumulateur.
Il ne vous reste donc qu'à compléter la méthode
- boolean equals(Enum x, Enum
y) qui teste si deux listes contiennent
exactement les mêmes éléments. On procédera ainsi,
récursivement :
- si les deux listes sont vides, alors la
comparaison est positive ;
- si l'une des deux listes vient à s'épuiser, alors la comparaison est négative
;
- sinon, on vérifie si le premier maillon
de x et le premier maillon
de y contiennent le même entier ; si ce
n'est pas le cas, la comparaison est négative ;
si en revanche c'est le cas, il faut continuer
la vérification avec, et pour
x et pour y, les entiers se
trouvant dans l'arbre du premier maillon et les
entiers se trouvant dans les maillons suivant. A
vous de trouver comment (mais il sera utile de
se servir du constructeur Enum
build(TreeNode t, Enum acc)).
|
public class Enum {
final int root;
final TreeNode right;
final Enum next;
public Enum(int root, TreeNode right, Enum next) {
this.root = root;
this.right = right;
this.next = next;
}
static Enum build(TreeNode t, Enum acc) {
throw new Error("A completer: exo 2");
}
static boolean equals(Enum x, Enum y) {
throw new Error("A completer: exo 2");
}
}
|
Pour tester votre code, utilisez la fonction
test4()
(classe
TestBSTSet).
Testing equality
b2=[ 1 4 5 7 14 16 17 18]
b1=[ 1 4 5 7 14 16 17 18]
b1==b2? true
b2==b1? true
Updating b2
b2=[ 1 4 5 7 14 15 16 17 18]
b1=[ 1 4 5 7 14 16 17 18]
b1==b2? false
b2==b1? false
s1= [ 2 17 23 34 56 67 77 99]
s2= [ 2 17 23 34 56 67 77 99]
s1=s2? true
Déposez le fichier Enum.java :
Nous vous proposons une solution pour les
classes TreeNode
et Enum.







