Interpolation de formes tridimensionnelles
Projet réalisé par
Pierre-Alexandre Pont et Mathieu Brédif (promo 2000)
Description du projet
Le but du projet est de réaliser l'interpolation
de deux formes polyhèdrales tridimensionnelles données. Ces fichiers doivent
être lisibles par Geomview. Le programme que nous avons
réalisé est en fait totalement interfacé avec Geomview. Il s'utilise comme un
module externe.Un tel "morphing" de formes tridimensionnelles peut par
exemple servir à réaliser des effets spéciaux pour des films, ou être une
fonctionnalité d'un logiciel de modélisation 3D. C'est en effet, une fois qu'on
a modélisé des objets tridimensionnels, une façon simple de réaliser des
animations.
Le principe de la technique utilisée est exposé dans l'article
[1]. L'article [2] présente des
améliorations qui rendent l'algorithme à la fois plus rapide et plus robuste.
Plus de détails...
Algorithmes utilisés
Le principal problème est de trouver
une géométrie (points/arêtes/faces) commune aux deux objets, c'est-à-dire les contenant toutes les
deux modulo une projection sur la sphère unité. Pour s'assurer que l'affichage de l'interpolation ne poserait pas de
problèmes, nous avons également choisi de faire en sorte que cette géométrie soit
une triangulation (ce problème est seulement évoqué dans les articles cités en
référence). Les étapes de l'algorithme utilisé sont les suivantes (elles suivent
pour l'essentiel l'article [2]):
lire les deux fichiers décrivant les objets
calculer toutes les intersections entre les demi-plans contenant les
arêtes des deux objets, attribuer à chaque arête de l'objet 0 la liste triée
de ses intersections et déterminer sur quelle face de l'objet 1 se projette
chaque point de l'objet 0
à partir des résultats de l'étape précédente, attribuer à chaque arête de
l'objet 1 la liste triée de ses intersections et déterminer sur quelle face de
l'objet 0 se projette chaque point de l'objet 1 (grâce à un tri effectué
seulement à partir des informations topologiques)
retrianguler la géométrie de l'objet 0 afin de créer une géométrie commune
aux deux objets
calculer pour chaque point de la géométrie commune (les points des deux
géométries et les points d'intersection trouvés) les coordonnées initiales et
finales
interpoler ces coordonnées et afficher la transformation de l'objet 0 en
l'objet 1
Plus de détails...
Résultats obtenus
Les objets à interpoler doivent respecter les critères suivants :
être homéomorphes à la sphères unités
être étoilés en 0
être triangulés (pas de face à plus de trois sommets)
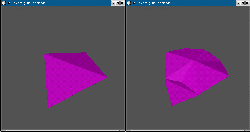
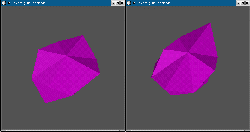
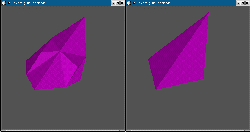
Voici deux exemples élémentaires où le programme fonctionne parfaitement :
transformation d'un tétraèdre en un autre tétraèdre résultat de son
homothétie par l'origine
transformation d'un cube en octaèdre
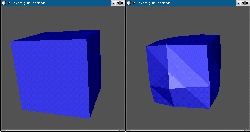
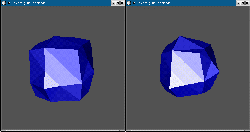
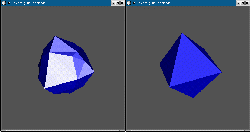
L'interfaçage avec Geomview permet de voir l'animation directement dans la
fenêtre "Camera".
Problèmes rencontrés et solutions apportées
Les deux
phases qui nous ont posé le plus de problèmes ont été :
la programmation de la triangulation finale (ce point n'était pas du tout
traité dans les articles) (plus de détails sur la
triangulation)
le déboguage qui ne pouvait se faire au fur et à mesure de l'avancement de
l'écriture du programme.
D'ailleurs le déboguage n'est pas totalement terminé puisque le programme
reconnaît encore imparfaitement les cas particuliers. Ces cas particuliers,
qui font boucler ou échouer le programme, sont principalement un point qui se
projette sur l'arête de l'autre objet ou deux arêtes qui sont sur un unique
plan contenant aussi l'origine. Pour essayer d'empêcher cela, nous effectuons
une "petite" rotation aléatoire sur un des objets avant de démarrer
l'algorithme.
Améliorations à apporter
En plus bien sûr du déboguage finl du programme, voilà quelques
améliorations que nous aimerions lui apporter :
comme suggéré dans l'énoncé, reconnaître les éléments de la géométrie
des objets permettant de détecter leur similitude afin de pouvoir effectuer
une éventuelle rotation simplifiant l'interpolation à effectuer
remplacer l'interpolation linéaire par une interpolation courbe telle
que le chemin suivi par un point lors de l'interpolation soit tangent à ses
deux extrémités aux normales des deux objets en ce point
réfléchir à une méthode de réduction d'un objet non étoilé à un objet
étoilé
Références
[1] Kent J., Parent R. et Carlson W., "Establishing correspondences by
topological merging : a new approach to 3-D shape transformation", Graphics
Interface '91, pp. 271-277
[2] Kent J., Parent R. et Carlson W., "Shape transformation for polyhedral
objects", Computer Graphics Vol. 26, No. 2, July 1992, pp. 47-54
Retour à la liste des projets réalisés
Quelques compléments :
Description du programme
Le programme se présente sous la forme de trois fichiers .c (3dmorph.c, basic.c, fichiers.c) et de deux fichiers .h (basic.h, fichiers.h). Le module
basic.h contient les définitions de types et les fonctions basiques de gestion
de ces types telles que la création de nouvelles listes. Le module fichiers.h
contient toutes les fonctions servant à la gestion des fichiers et plus
particulièrement à l'interfaçage du programme avec Geomview.
Utilisation du programme
Le programme peut être utilisé comme un module externe de Geomview ou
directement en ligne de commandes :
module externe de Geomview : il faut que le répertoire où se situe le
programme contienne un fichier .geomview contenant la ligne : (e-module
define "3DMorph" ".\3dmorph"). Il suffit alors de lancer Geomview, de
charger deux fichiers et de cliquer sur 3DMorph
ligne de commande : il faut indiquer en paramètre les deux fichiers au
format .geom à lire. Le programme écrit un fichier "3dmorph.geom"
correspondant à l'étape intermédiaire de l'interpolation.
Quelques détails sur les algorithmes
Les articles cités en référence recommandent de projeter les deux
géométries sur la sphère de rayon 1 pour effectuer les calculs
d'intersection des arêtes. Nous avons décidé de ne pas effectuer cette
projection et de mener les calculs comme si on raisonnait sur les classes d'équivalence contenant les
points situés sur un même rayon issu de l'origine. Ainsi la détermination de
l'existence ou non d'une intersection entre deux arêtes se fait non
pas en considérant la projection de ces arêtes sur la sphère unité mais en
considérant les demi-plans contenant ces arêtes et l'origine :
l'intersection, si elle existe, n'est pas un point mais un rayon issu de
l'origine.
Conformément à l'article [2], la détermination de toutes les
intersections ne se fait pas en considérant tous les couples d'arêtes
(méthode envisagée par l'article [1]) mais par un parcours des arêtes de la
géométrie de l'objet 0. Cela permet de réduire la complexité de l'algorithme
de morphing.
Le tri des intersections sur les arêtes de l'objet 1 se fait également
grâce à un parcours des arêtes de la géométrie de l'objet 1, ce qui permet
de trouver dans le même temps les faces de l'objet 0 sur lesquels les points
de l'objet 1 se projettent.
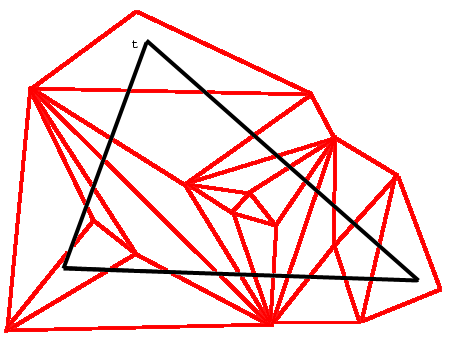
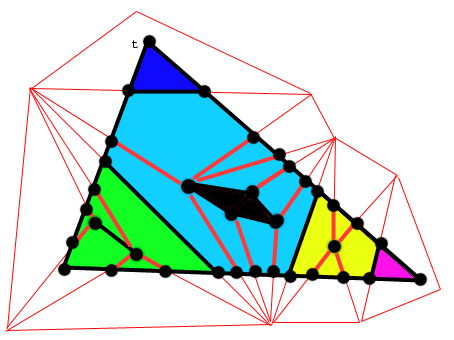
L'algorithme de triangulation
Qualifions de "noyau" dans un certain triangle t un point, une arête ou un
triangle entièrement contenu dans t. A un point d'intersection sur le bord de t
on fait correspondre un point noyau si l'arête de 0 qui forme ce point avec un
côté de t a un une extrémité qui est un noyau de t. Si une intersection n'a pas
de point associé qui soit un noyau de t, c'est donc que son arête coupe t de
part en part.
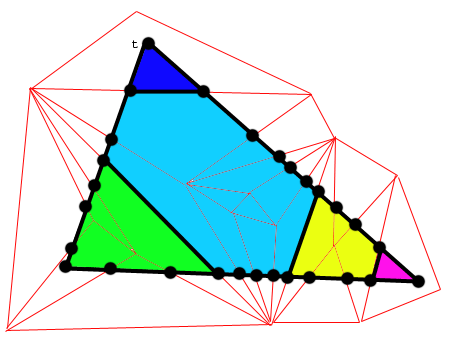
Chaque triangle de l'objet 1 se divise en "cellules" dont les sommets sont de
l'objet 1 ou des points d'intersection; on découpe chaque triangle dès que l'on
trouve une arête qui le coupe de part en part. Dans une cellule données, qui n'a
donc plus d'arête la scindant en deux, soit aucun point du bord n'a de point
associé qui soit noyau de t et donc la cellule est un polygone, soit il existe
des points du noyau à l'intérieur de cette cellule. Il suffit alors de recopier
tels quels les triangles de l'objet 0 qui sont noyaux de t, et de triangulariser
les polygones entourant ce noyau.
....
Nous contacter
Mathieu Brédif -
Pierre-Alexandre Pont










