Majeure "Algèbre, Informatique et Applications" Enseignement d'Approfondissement "Géométrie et Synthèse d'Images"

Description du projet

    L'objectif est d'implémenter un algorithme de simplification de maillages 3D triangulaires. Le résultat doit naturellement être aussi proche que possible du maillage d'origine. On introduit donc une fonction d'énergie qui évalue la distance entre un modèle (par exemple le maillage d'origine) et le maillage courant. A chaque étape, on propose un certain nombre de suppressions d'arêtes, et on choisit celle qui minimise cette énergie. On peut ainsi choisir exactement le nombre de sommets finaux (-1 à chaque fois), et ouvrir la porte aux "maillages progressifs" : il s'agit d'un format de fichier qui indique les arêtes successives à ajouter à un maillage M0 contenant peu de sommets, pour obtenir le maillage voulu (l'équivalent du jpeg progressif). L'intérêt de la simplification de maillage et des maillages progressifs est énorme sur Internet par exemple (ne pas avoir à attendre que toute l'image soit transférée pour commencer à l'afficher).

Algorithme utilisé

1. Association Arête→Energie :

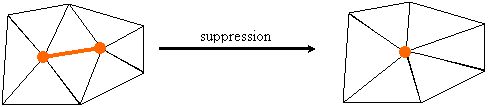
Evidemment, cela nécessite de choisir la position du sommet final résultant du regroupement des 2 sommets bordant l'arête. Pour cela, on utilise l'algorithme suivant, dont on peut montrer qu'il converge :

• On choisit pour le sommet final une position simple (ex. : milieu entre les 2 sommets de l'arête avant suppression)
• Faire i fois (i=15 ou 20 en pratique) :
  • Pour chaque point de référence p_i (sommet du maillage de départ ici) : détermination de son projeté sur le maillage courant. On garde ses coordonnées barycentriques b_i par rapport aux sommets du maillages (seuls les 3 bi du triangle concerné sont non nuls).

   

  • Ces coordonnées barycentriques b_i étant fixées, on peut calculer explicitement la position du sommet qui minimise l'énergie E suivante :

E = E_dist + E_spring

avec E_dist =  _Σ ║p_i - Φ_M(b_i)║²

    et E_spring= Σ (longueurs des arêtes)

où Φ_M(b_i) est la position du projeté du point de référence Pi sur le maillage M. Le terme Espring permet de régulariser la fonction d'énergie et d'assurer l'existence d'un minimum.

On peut lancer cet algorithme avec les 3 positions simples pour le sommet final, et retenir ainsi l'énergie minimale que l'on obtient en supprimant cette arête.

2. Suppressions d'arêtes successives

• On crée alors une pile P contenant un certain nombre d'arêtes supprimables, prises au hasard, et classées par énergie croissante en partant de la tête de P.

• on supprime l'arête qui est en tête de la pile

• on retire de la pile toutes les arêtes dont les énergies se trouvent modifiées (voisinage de la suppression)

•  on rajoute dans la pile autant d'arêtes qu'on en a supprimé, en les prenant au hasard, et en veillant à les classer selon l'énergie qui leur est associée
• on supprime l'arête du haut... et on itère autant de fois que l'on veut.

Résultats obtenus

Le programme de simplification de maillage fonctionne bien, comme on peut le constater sur les images ci dessous. La forme générale est bien conservée. Toutefois, sa rapidité peut être notablement augmentée en remaniant les parties "lourdes" du programme, et en adoptant des heuristiques qu'il conviendrait de mettre au point au fil des expérimentations. La rapidité de l'algorithme n'était pas mon objectif premier, et n'a pas constitué d'obstacle pour l'analyse des résultats (de l'ordre de quelques secondes pour des grosses simplifications).

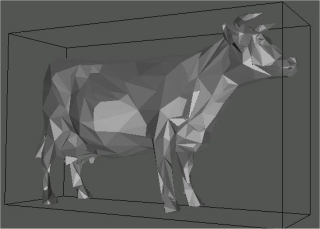
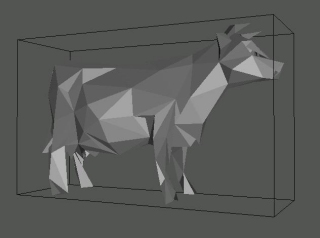
    J'ai travaillé sur un maillage d'origine représentant une vache avec 2907 sommets (1^ère image), que j'ai successivement réduit à 800, 200 et 40 sommets (on notera qu'il est aisé de choisir le nombre exact de sommets pour le maillage simplifié)

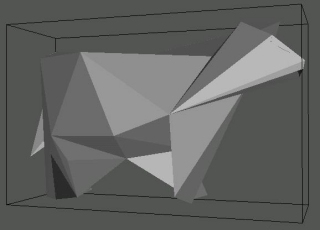
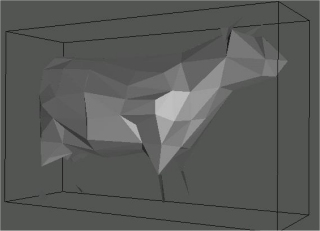
    A titre de comparaison, voici les simplifications obtenues avec un autre algorithme, beaucoup plus simple, réalisé lors d'un TD du cours, qui quadrille un cube contenant le maillage de manière régulière et regroupe les points qui sont dans le même cube (donc on ne choisit pas facilement le nombre de sommets finaux). On remarque que les détails disparaissent complètement, comme par exemple les pattes de la vache.

Problèmes rencontrés et solutions apportées

    La gestion des relations entre les triangles du maillage, comme par exemple les relations de voisinage, est très importante et pas toujours évidente. Il y a de nombreux cas particuliers... Il faut donc essayer de trouver les règles les plus générales possibles et faire un peu de théorie géométrique. En outre, la première partie de mon programme est entièrement consacrée à la lecture du fichier geomview et à la détermination de toutes les relations liant sommets, triangles, et points de référence.

    De manière assez surprenante, c'est un problème de géométrie de base qui m'a posé le plus de problème : comment projeter un point 3D sur un triangle dont on connaît les positions des sommets, de manière à obtenir ses coordonnées barycentriques en fonction des 3 sommets. Après avoir essayé en vain de faire des calculs explicites (les gros calculs n'ont jamais été mon fort), j'ai tenté d'implémenter une espèce d'algorithme du gradient. Il fonctionnait, mais la convergence n'était pas assurée pour toutes les tailles et formes de triangles. Donc j'ai abandonné cette méthode, et découpé le triangle en un certain nombre de paramétrisations dont je prends la plus proche du point 3D de référence.

Bibliographie

Mesh optimization de Hugues Hoppe, Tony DeRose, Tom Duchamp, John McDonald et Werner Stuetzle
Progressive Meshes de Hugues Hoppe