


Dans ce chapitre nous allons décrire quelques façons classiques de paralléliser certains calculs d'algèbre
linéaire. Ceux-ci ont été particulièrement étudiés car de très nombreux codes scientifiques, requiérant une grande puissance de calcul, utilisent
des calculs matriciels, de façon intensive.
10.1 Produit matrice-vecteur sur anneau
On cherche à calculer y=Ax, où
A est une matrice de dimension n × n,
x est un vecteur à n composantes (de 0 à n-1), le tout
sur un anneau de p processeurs, avec r=n/p entier.
Le programme séquentiel est simple.
En effet, le calcul du produit matrice-vecteur revient au calcul de n produits scalaires:
for (i=1;i<=n;i++)
for (j=1;j<=n;j++)
y[i] = y[i]+a[i,j]*x[j];
On essaie donc de
distribuer le calcul des produits scalaires aux différents processeurs.
Chaque processeur a en mémoire r lignes de la matrice A rangées dans une matrice
a de dimension r × n.
Le processeur Pq contient
les lignes qr à (q+1)r-1 de la matrice A et les composantes de même
rang des vecteurs x et y:
float a[r][n];
float x[r],y[r];
Le programme distribué correspondant à la parallélisation de cet algorithme
séquentiel est:
matrice-vecteur(A,x,y) {
q = my_num();
p = tot_proc_num();
for (step=0;step<p;step++) {
send(x,r);
for (i=0;i<r;i++)
for (j=0;j<r;j++)
y[i] = y[i]+a[i,(q-step mod p)r+j]*x[j];
receive(temp,r);
x = temp;
}
}
Donnons un exemple des différentes étapes (boucle extérieure, sur step), pour n=8.
La distribution initiale des données est donc comme suit:
| P0 |
æ
è |
| A00 |
A01 |
A02 |
A03 |
A04 |
A05 |
A06 |
A07 |
| A10 |
A11 |
A12 |
A13 |
A14 |
A15 |
A16 |
A17 |
|
|
ö
ø |
|
|
|
| |
| P1 |
æ
è |
| A20 |
A21 |
A22 |
A23 |
A24 |
A25 |
A26 |
A27 |
| A30 |
A31 |
A32 |
A33 |
A34 |
A35 |
A36 |
A37 |
|
|
ö
ø |
|
|
|
| |
| P2 |
æ
è |
| A40 |
A41 |
A42 |
A43 |
A44 |
A45 |
A46 |
A47 |
| A50 |
A51 |
A52 |
A53 |
A54 |
A55 |
A56 |
A57 |
|
|
ö
ø |
|
|
|
| |
| P3 |
æ
è |
| A60 |
A61 |
A62 |
A63 |
A64 |
A65 |
A66 |
A67 |
| A70 |
A71 |
A72 |
A73 |
A74 |
A75 |
A76 |
A77 |
|
|
ö
ø |
|
|
A la première étape, chacun des p=4 processeurs considère les sous-matrices
suivantes:
| P0 |
æ
è |
| A00 |
A01 |
· |
· |
· |
· |
· |
· |
| A10 |
A11 |
· |
· |
· |
· |
· |
· |
|
|
ö
ø |
|
|
temp |
¬ |
|
|
| |
| P1 |
æ
è |
| · |
· |
A22 |
A23 |
· |
· |
· |
· |
| · |
· |
A32 |
A33 |
· |
· |
· |
· |
|
|
ö
ø |
|
|
temp |
¬ |
|
|
| |
| P2 |
æ
è |
| · |
· |
· |
· |
A44 |
A45 |
· |
· |
| · |
· |
· |
· |
A54 |
A55 |
· |
· |
|
|
ö
ø |
|
|
temp |
¬ |
|
|
| |
| P3 |
æ
è |
| · |
· |
· |
· |
· |
· |
A66 |
A67 |
| · |
· |
· |
· |
· |
· |
A76 |
A77 |
|
|
ö
ø |
|
|
temp |
¬ |
|
A la deuxième étape, les processeurs ont en mémoire les sous-matrices suivantes:
| P0 |
æ
è |
| · |
· |
· |
· |
· |
· |
A06 |
A07 |
| · |
· |
· |
· |
· |
· |
A16 |
A17 |
|
|
ö
ø |
|
|
temp |
¬ |
|
|
| |
| P1 |
æ
è |
| A20 |
A21 |
· |
· |
· |
· |
· |
· |
| A30 |
A31 |
· |
· |
· |
· |
· |
· |
|
|
ö
ø |
|
|
temp |
¬ |
|
|
| |
| P2 |
æ
è |
| · |
· |
A42 |
A43 |
· |
· |
· |
· |
| · |
· |
A52 |
A53 |
· |
· |
· |
· |
|
|
ö
ø |
|
|
temp |
¬ |
|
|
| |
| P3 |
æ
è |
| · |
· |
· |
· |
A64 |
A65 |
· |
· |
| · |
· |
· |
· |
A74 |
A75 |
· |
· |
|
|
ö
ø |
|
|
temp |
¬ |
|
Puis à la troisième étape:
| P0 |
æ
è |
| · |
· |
· |
· |
A04 |
A05 |
· |
· |
| · |
· |
· |
· |
A14 |
A15 |
· |
· |
|
|
ö
ø |
|
|
temp |
¬ |
|
|
| |
| P1 |
æ
è |
| · |
· |
· |
· |
· |
· |
A26 |
A27 |
| · |
· |
· |
· |
· |
· |
A36 |
A37 |
|
|
ö
ø |
|
|
temp |
¬ |
|
|
| |
| P2 |
æ
è |
| A40 |
A41 |
· |
· |
· |
· |
· |
· |
| A50 |
A51 |
· |
· |
· |
· |
· |
· |
|
|
ö
ø |
|
|
temp |
¬ |
|
|
| |
| P3 |
æ
è |
| · |
· |
A62 |
A63 |
· |
· |
· |
· |
| · |
· |
A72 |
A73 |
· |
· |
· |
· |
|
|
ö
ø |
|
|
temp |
¬ |
|
Enfin à la quatrième étape:
| P0 |
æ
è |
| · |
· |
A02 |
A03 |
· |
· |
· |
· |
| · |
· |
A12 |
A13 |
· |
· |
· |
· |
|
|
ö
ø |
|
|
temp |
¬ |
|
|
| |
| P1 |
æ
è |
| · |
· |
· |
· |
A24 |
A25 |
· |
· |
| · |
· |
· |
· |
A34 |
A35 |
· |
· |
|
|
ö
ø |
|
|
temp |
¬ |
|
|
| |
| P2 |
æ
è |
| · |
· |
· |
· |
· |
· |
A46 |
A47 |
| · |
· |
· |
· |
· |
· |
A56 |
A57 |
|
|
ö
ø |
|
|
temp |
¬ |
|
|
| |
| P3 |
æ
è |
| A60 |
A61 |
· |
· |
· |
· |
· |
· |
| A70 |
A71 |
· |
· |
· |
· |
· |
· |
|
|
ö
ø |
|
|
temp |
¬ |
|
En notant ta le temps de calcul élémentaire,
tc le temps de communication élémentaire, on se propose d'estimer le temps de
calcul de cet algorithme, donc de mesurer ses performances.
Il y a p étapes identiques dans cet algorithme,
chacune de temps égal au temps le plus long parmi le temps de calcul local et le temps
de communication: max(r2 ta,b+rtc).
On obtient donc un temps total de p*max(r2 ta,b+rtc).
Quand n est assez grand, r2 ta devient prépondérant, d'où asympotiquement un temps
de n2/pta. C'est-à-dire que asymptotiquement, l'efficacité tend vers 1 !
Remarquez que l'on aurait
aussi pu procéder à un échange total de x au début.
10.2 Factorisation LU
On cherche maintenant à résoudre un système linéaire dense
Ax=b par triangulation de Gauss. Un programme séquentiel qui implémente cela est:
for (k=0;k<n-1;k++) {
prep(k): for (i=k+1;i<n;i++)
a[i,k]=a[i,k]/a[k,k];
for (j=k+1;j<n;j++)
update(k,j): for (i=k+1;i<n;i++)
a[i,j]=a[i,j]-a[i,k]*a[k,j];
}
On le parallélise en distribuant les colonnes aux différents processeurs.
On va supposer que cette distribution nous est donnée par une fonction alloc telle
que alloc(k)=q veut dire que la kième colonne est affectée à la mémoire locale
de Pq.
On utilisera la fonction broadcast, pour faire en sorte qu'à l'étape k, le processeur
qui possède la colonne k la diffuse à tous les autres.
On va supposer dans un premier temps que alloc(k)=k. On obtient alors:
q = my_num();
p = tot_proc_num();
for (k=0;k<n-1;k++) {
if (k == q) {
prep(k): for (i=k+1;i<n;i++)
buffer[i-k-1] = a[i,k]/a[k,k];
broadcast(k,buffer,n-k);
}
else {
receive(buffer,n-k);
update(k,q): for (i=k+1;k<n;k++)
a[i,q] = a[i,q]-buffer[i-k-1]*a[k,q]; }
}
Dans le cas plus général, il faut gérer les indices dans les blocs de colonnes.
Maintenant chaque processeur gère r=n/p colonnes, avec des indices locaux:
q = my_num();
p = tot_proc_num();
l = 0;
for (k=0;k<n-1;k++) {
if (alloc(k) == q) {
prep(k): for (i=k+1;i<n;i++)
buffer[i-k-1] = a[i,l]/a[k,l];
l++; }
broadcast(alloc(k),buffer,n-k);
for (j=l;j<r;j++)
update(k,j): for (i=k+1;k<n;k++)
a[i,j] = a[i,j]-buffer[i-k]*a[k,j]; }
Cet algorithme présente néanmoins un certain nombre de défauts.
Premièrement, le nombre de données varie au cours des étapes (il y en a de moins en moins).
Ensuite, le volume de calcul n'est pas proportionnel au volume des données: quand un processeur
a par exemple r colonnes consécutives, le dernier processeur a moins de calcul (que de données)
par rapport au premier.
Il faudrait donc trouver une fonction
d'allocation qui réussisse à équilibrer le volume des données
et du travail!
Cet équilibrage de charge doit être réalisé
à chaque étape de l'algorithme, et pas seulement de façon globale.
10.2.1 Cas de l'allocation cyclique par lignes
Pour p=4, et n=8 on a la répartition initiale des données comme suit:
æ
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
è |
| P0 |
P1 |
P2 |
P3 |
P0 |
P1 |
P2 |
P3 |
| A00 |
A01 |
A02 |
A03 |
A04 |
A05 |
A06 |
A07 |
| A10 |
A11 |
A12 |
A13 |
A14 |
A15 |
A16 |
A17 |
| A20 |
A21 |
A22 |
A23 |
A24 |
A25 |
A26 |
A27 |
| A30 |
A31 |
A32 |
A33 |
A34 |
A35 |
A36 |
A37 |
| A40 |
A41 |
A42 |
A43 |
A44 |
A45 |
A46 |
A47 |
| A50 |
A51 |
A52 |
A53 |
A54 |
A55 |
A56 |
A57 |
| A60 |
A61 |
A62 |
A63 |
A64 |
A65 |
A66 |
A67 |
| A70 |
A71 |
A72 |
A73 |
A74 |
A75 |
A76 |
A77 |
|
ö
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
ø |
A k=0:
æ
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
è |
| P0: p0; b |
P1 |
P2 |
P3 |
P0 |
P1 |
P2 |
P3 |
| U00 |
A01 |
A02 |
A03 |
A04 |
A05 |
A06 |
A07 |
| L10 |
A11 |
A12 |
A13 |
A14 |
A15 |
A16 |
A17 |
| L20 |
A21 |
A22 |
A23 |
A24 |
A25 |
A26 |
A27 |
| L30 |
A31 |
A32 |
A33 |
A34 |
A35 |
A36 |
A37 |
| L40 |
A41 |
A42 |
A43 |
A44 |
A45 |
A46 |
A47 |
| L50 |
A51 |
A52 |
A53 |
A54 |
A55 |
A56 |
A57 |
| L60 |
A61 |
A62 |
A63 |
A64 |
A65 |
A66 |
A67 |
| L70 |
A71 |
A72 |
A73 |
A74 |
A75 |
A76 |
A77 |
|
ö
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
ø |
Puis, toujours à k=0:
æ
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
è |
| P1: r;u0,1 |
P2: r; u0,2 |
P3: r; u0,3 |
P0: u0,4 |
P1 |
P2 |
P3 |
| U00 |
U01 |
U02 |
U03 |
U04 |
A05 |
A06 |
A07 |
| L10 |
A11' |
A12' |
A13' |
A14' |
A15 |
A16 |
A17 |
| L20 |
A21' |
A22' |
A23' |
A24' |
A25 |
A26 |
A27 |
| L30 |
A31' |
A32' |
A33' |
A34' |
A35 |
A36 |
A37 |
| L40 |
A41' |
A42' |
A43' |
A44' |
A45 |
A46 |
A47 |
| L50 |
A51' |
A52' |
A53' |
A54' |
A55 |
A56 |
A57 |
| L60 |
A61' |
A62' |
A63' |
A64' |
A65 |
A66 |
A67 |
| L70 |
A71' |
A72' |
A73' |
A74' |
A75 |
A76 |
A77 |
|
ö
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
ø |
Ensuite:
æ
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
è |
| P0 |
P1 |
P2 |
P3 |
P0 |
P1: r; u0,5 |
P2: r; u0,6 |
P3: r; u0,7 |
| U00 |
U01 |
U02 |
U03 |
U04 |
U05 |
U06 |
U07 |
| L10 |
A11' |
A12' |
A13' |
A14' |
A15' |
A16' |
A17' |
| L20 |
A21' |
A22' |
A23' |
A24' |
A25' |
A26' |
A27' |
| L30 |
A31' |
A32' |
A33' |
A34' |
A35' |
A36' |
A37' |
| L40 |
A41' |
A42' |
A43' |
A44' |
A45' |
A46' |
A47' |
| L50 |
A51' |
A52' |
A53' |
A54' |
A55' |
A56' |
A57' |
| L60 |
A61' |
A62' |
A63' |
A64' |
A65' |
A66' |
A67' |
| L70 |
A71' |
A72' |
A73' |
A74' |
A75' |
A76' |
A77' |
|
|
ö
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
ø |
Maintenant, quand k=1:
æ
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
è |
| P0 |
P1: p1; b |
P2 |
P3 |
P0 |
P1 |
P2 |
P3 |
| U00 |
U01 |
U02 |
U03 |
U04 |
U05 |
U06 |
U07 |
| L10 |
U11 |
A12' |
A13' |
A14' |
A15' |
A16' |
A17' |
| L20 |
L21 |
A22' |
A23' |
A24' |
A25' |
A26' |
A27' |
| L30 |
L31 |
A32' |
A33' |
A34' |
A35' |
A36' |
A37' |
| L40 |
L41 |
A42' |
A43' |
A44' |
A45' |
A46' |
A47' |
| L50 |
L51 |
A52' |
A53' |
A54' |
A55' |
A56' |
A57' |
| L60 |
L61 |
A62' |
A63' |
A64' |
A65' |
A66' |
A67' |
| L70 |
L71 |
A72' |
A73' |
A74' |
A75' |
A76' |
A77' |
|
|
ö
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
ø |
Puis, toujours à k=1:
æ
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
è |
| P0 |
P1 |
P2: r; u1,2 |
P3: r; u1,3 |
P0: r; u1,4 |
P1 |
P2 |
P3 |
|
| U00 |
U01 |
U02 |
U03 |
U04 |
U05 |
U06 |
U07 |
| L10 |
U11 |
U12 |
U13 |
U14 |
A15' |
A16' |
A17' |
| L20 |
L21 |
A22'' |
A23'' |
A24'' |
A25' |
A26' |
A27' |
| L30 |
L31 |
A32'' |
A33'' |
A34'' |
A35' |
A36' |
A37' |
| L40 |
L41 |
A42'' |
A43'' |
A44'' |
A45' |
A46' |
A47' |
| L50 |
L51 |
A52'' |
A53'' |
A54'' |
A55' |
A56' |
A57' |
| L60 |
L61 |
A62'' |
A63'' |
A64'' |
A65' |
A66' |
A67' |
| L70 |
L71 |
A72'' |
A73'' |
A74'' |
A75' |
A76' |
A77' |
|
|
ö
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
ø |
Faisons un calcul de complexité dans le cas particulier p=n.
Donc, ici, alloc(k)==k.
Le coût de la mise à jour (update) de la colonne j par le processeur j
est de
n-k-1 pour l'étape k (éléments en position k+1 à n-1).
Ceci étant fait pour toutes les étapes k=0 à k=n-1.
D'où un coût total de
Pour ce qui est du temps de calcul;
le chemin critique d'exécution est:
prep0(0)® update1(0,1), prep1(1) ® update2(1,2), prep2(2) ® ...
C'est comme si on faisait environ r fois le travail dans le cas d'une
allocation cyclique pour r=n/p processeurs.
Remarquez que l'on obtient bien un recouvrement des communications, mais pas entre
les communications et le calcul! C'est ce que l'on va améliorer dans la prochaine version
de l'algorithme distribué.
On a donc les coûts suivants:
nb+n2/2tc+O(1) pour les n-1 communications (transportant de l'ordre de
n2 données),
n2/2ta+O(1) pour les prep et
pour l'update des r colonnes sur le processeur j mod p, en parallèle sur tous les
processeurs,
environ rn(n-1)/2.
On obtient donc un coût final de l'ordre de n3/2p pour les update des p processeurs: c'est le terme dominant
si p<<n et l'efficacité est excellente asymptotiquement (pour n grand).
10.2.2 Recouvrement communication/calcul
On peut décomposer le broadcast afin de réaliser un meilleur recouvrement
entre les communications et le calcul, comme suit:
q = my_num();
p = tot_proc_num();
l = 0;
for (k=0;k<n-1;k++) {
if (k == q mod p) {
prep(k): for (i=k+1;i<n;i++)
buffer[i-k-1] = -a[i,l]/a[k,l];
l++; send(buffer,n-k); }
else { receive(buffer,n-k);
if (q != k-1 mod p) send(buffer,n-k); }
for (j=l;j<r;j++)
update(k,j): for (i=k+1;k<n;k++)
a[i,j] = a[i,j]+buffer[i-k-1]*a[k,j]; }
Il reste néanmoins un défaut.
Regardons ce qui se passe sur P1:
-
A l'étape k=0: P1 reçoit la colonne pivot 0 de P0
- P1 l'envoit à P2
- Fait update(0,j) pour toutes les colonnes j qui lui appartiennent, c'est-à-dire j=1 mod p
- A l'étape k=1: fait prep(1)
- Envoie la colonne pivot 1 à P2
- Fait update(1,j) pour toutes les colonnes j qui lui appartiennent, c'est-à-dire j=1 mod p
- etc.
On obtient donc les actions en parallèle suivantes, au cours du temps:
| P0 |
P1 |
P2 |
P3 |
| prep(0) |
|
|
|
| send(0) |
receive(0) |
|
|
| update(0,4) |
send(0) |
receive(0) |
|
| update(0,8) |
update(0,1) |
send(0) |
receive(0) |
| update(0,12) |
update(0,5) |
update(0,2) |
update(0,3) |
| |
update(0,9) |
update(0,6) |
update(0,7) |
| |
update(0,13) |
update(0,10) |
update(0,11) |
| |
prep(1) |
update(0,14) |
update(0,15) |
| |
send(1) |
receive(1) |
|
| |
update(1,5) |
send(1) |
receive(1) |
| receive(1) |
update(1,9) |
update(1,2) |
send(1) |
| update(1,4) |
update(1,13) |
update(1,6) |
update(1,3) |
| update(1,8) |
|
update(1,10) |
update(1,7) |
| update(1,12) |
|
update(1,14) |
update(1,11) |
| ... |
... |
... |
... |
Alors que
P1 aurait pu faire:
-
update(0,1)
- prep(1)
- Envoi vers P2
- update(0,j) pour j=1 mod p et j>1
- etc.
Et on obtiendrait, toujours sur quatre processeurs:
| P0 |
P1 |
P2 |
P3 |
| prep(0) |
|
|
|
| send(0) || up(0,4) |
receive(0) |
|
|
| up(0,8) |
send(0) || up(0,1) |
receive(0) |
|
| up(0,12) |
prep(1) |
send(0) || up(0,2) |
receive(0) |
| |
send(1) || up(0,5) |
receive(1) || up(0,6) |
up(0,3) |
| |
up(0,9) |
send(1) || up(0,10) |
receive(1) || up(0,7) |
| receive(1) |
up(0,13) |
up(0,14) |
send(1) || up(0,11) |
| up(1,4) |
up(1,5) |
up(1,2) |
up(0,15) |
| up(1,8) |
up(1,9) |
prep(2) |
up(1,3) |
| up(1,12) |
up(1,13) |
send(2) || up(1,6) |
receive(2) || up(1,7) |
| receive(2) |
|
up(1,10) |
send(2) || up(1,11) |
| send(2) || up(2,4) |
receive(2) |
up(1,14) |
up(1,15) |
| ... |
... |
... |
... |
Ce qui est bien mieux!
10.3 Algorithmique sur grille 2D
On va maintenant examiner trois algorithmes classiques de produit de matrices
sur une grille 2D, les
algorithmes de Cannon,
de Fox,
et de Snyder.
On cherche donc à calculer
C=C+AB, avec A, B et C de taille N × N.
Soit p=q2: on dispose d'une grille de processeurs en tore de taille q × q. On
distribue les matrices par blocs: Pij stocke Aij, Bij
et Cij.
La distribution des données peut se faire,
par blocs, et/ou de façon cyclique. La distribution par blocs
permet d'augmenter le grain de calcul et d'améliorer l'utilisation
des mémoires hiérarchiques. La
distribution cyclique, elle, permet de mieux équilibrer la charge.
On définit maintenant une distribution cyclique par blocs, de façon générale.
On suppose que l'on souhaite répartir un vecteur à M composantes sur p processeurs, à chaque
entrée 0 £ m < M on va associer trois indices, le numéro de processeur 0 £ q < p
sur lequel se trouve cette composante, le numéro de bloc b et l'indice i dans ce bloc:
| m |
® |
| (q,b,i)= |
æ
ç
ç
è |
ë |
|
û, ë
|
|
û, m mod r |
ö
÷
÷
ø |
|
où r est la taille de bloc et T=rp.
Par exemple, un réseau linéaire par blocs (4 processeurs) avec
M=8, p=4, et r=8 (pour chaque colonne) donnerait la répartition suivante:
| 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
| 2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
| 3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
| 3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
0u encore, un réseau linéaire cyclique (4 processeurs) avec
M=8, p=4, r=4 (pour chaque colonne) donnerait:
| 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
| 3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
| 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
| 3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
Autre exemple, un réseau en grille 2D par blocs (4×4 processeurs) avec
M=8, p=4, r=8 en ligne et en colonne, donnerait:
| 0.0 |
0.0 |
0.1 |
0.1 |
0.2 |
0.2 |
0.3 |
0.3 |
| 0.0 |
0.0 |
0.1 |
0.1 |
0.2 |
0.2 |
0.3 |
0.3 |
| 1.0 |
1.0 |
1.1 |
1.1 |
1.2 |
1.2 |
1.3 |
1.3 |
| 1.0 |
1.0 |
1.1 |
1.1 |
1.2 |
1.2 |
1.3 |
1.3 |
| 2.0 |
2.0 |
2.1 |
2.1 |
2.2 |
2.2 |
2.3 |
2.3 |
| 2.0 |
2.0 |
2.1 |
2.1 |
2.2 |
2.2 |
2.3 |
2.3 |
| 3.0 |
3.0 |
3.1 |
3.1 |
3.2 |
3.2 |
3.3 |
3.3 |
| 3.0 |
3.0 |
3.1 |
3.1 |
3.2 |
3.2 |
3.3 |
3.3 |
Enfin, dernier exemple, un réseau en grille 2D par blocs cycliques, avec
M=8, p=4, r=4 en ligne et en colonne:
| 0.0 |
0.1 |
0.2 |
0.3 |
0.0 |
0.1 |
0.2 |
0.3 |
| 1.0 |
1.1 |
1.2 |
1.3 |
1.0 |
1.1 |
1.2 |
1.3 |
| 2.0 |
2.1 |
2.2 |
2.3 |
2.0 |
2.1 |
2.2 |
2.3 |
| 3.0 |
3.1 |
3.2 |
3.3 |
3.0 |
3.1 |
3.2 |
3.3 |
| 0.0 |
0.1 |
0.2 |
0.3 |
0.0 |
0.1 |
0.2 |
0.3 |
| 1.0 |
1.1 |
1.2 |
1.3 |
1.0 |
1.1 |
1.2 |
1.3 |
| 2.0 |
2.1 |
2.2 |
2.3 |
2.0 |
2.1 |
2.2 |
2.3 |
| 3.0 |
3.1 |
3.2 |
3.3 |
3.0 |
3.1 |
3.2 |
3.3 |
En pratique, les fonctions de calcul de produit matriciel (ou autres fonctions qu'on
voudrait typiquement mettre dans une librairie de calcul distribué) peuvent se faire
en
version centralisée ou distribuée. Dans la version centralisée,
les routines sont appelées avec les données et les résultats sur la machine hôte.
Cette version permet de minimiser le nombre de fonctions à écrire, et permet
de choisir la distribution des données la plus adaptée.
Mais, elle a un coût prohibitif si on enchaîne les appels.
Dans la version distribuée au contraire,
les données sont déjà distribuées, et le résultat l'est également.
Le passage à l'échelle est donc plus facile à obtenir,
par des fonctions de redistribution des données.
Mais il y a un compromis à trouver entre le coût de redistribution
plus le coût de l'algorithme avec
rangement adapté, avec le coût de l'algorithme avec un rangement non-adapté.
De façon générale, la redistribution des données est parfois incontournable, avec
des coûts potentiellement dissuasifs.
Par exemple, si on dispose
d'une FFT 1D, programmer une FFT 2D peut se faire en enchaînant les calculs sur les lignes
d'une matrice, puis sur les colonnes de la matrice ainsi obtenue (ou l'inverse). Chacune des étapes
est parfaitement parallèle, car le calcul des FFT 1D sur l'ensemble des lignes peut se faire avec
une efficacité 1, en allouant une ligne (ou plus généralement un paquet de lignes) par processeur.
Par contre, quand on veut faire la même chose ensuite par colonne, il faut calculer la transposée de la
matrice, ou dit de façon plus prosaïque, il faut réorganiser la matrice, afin qu'à chaque processeur
soit maintenant associé une colonne, ou un paquet de colonnes en général. Ceci implique une diffusion globale
qui peut être extrêmement couteuse, et arriver aux limites de la contention du réseau, ou du bus de
données interne.
Prenons un exemple pour le reste des explications algorithmiques de cette section. On
va supposer n=4, et C=0. On cherche donc à calculer:
æ
ç
ç
ç
è |
| C00 |
C01 |
C02 |
C03 |
| C10 |
C11 |
C12 |
C13 |
| C20 |
C21 |
C22 |
C23 |
| C30 |
C31 |
C32 |
C33 |
|
ö
÷
÷
÷
ø |
|
¬ |
æ
ç
ç
ç
è |
| A00 |
A01 |
A02 |
A03 |
| A10 |
A11 |
A12 |
A13 |
| A20 |
A21 |
A22 |
A23 |
| A30 |
A31 |
A32 |
A33 |
|
ö
÷
÷
÷
ø |
|
× |
æ
ç
ç
ç
è |
| B00 |
B01 |
B02 |
B03 |
| B10 |
B11 |
B12 |
B13 |
| B20 |
B21 |
B22 |
B23 |
| B30 |
B31 |
B32 |
B33 |
|
ö
÷
÷
÷
ø |
|
10.3.1 Principe de l'algorithme de Cannon
Le pseudo-code pour l'algorithme de Cannon est:
/* diag(A) sur col 0, diag(B) sur ligne 0 */
Rotations(A,B); /* preskewing */
/* calcul du produit de matrice */
forall (k=1; k<=sqrt(P)) {
LocalProdMat(A,B,C);
VerticalRotation(B,downwards);
HorizontalRotation(A,leftwards); }
/* mouvements des donnees apres les calculs */
Rotations(A,B); /* postskewing */
Expliquons sur notre exemple comment l'algorithme de Cannon fonctionne.
On commence par effectuer un ``preskewing'', pour obtenir les allocations des données
suivantes:
æ
ç
ç
ç
è |
| C00 |
C01 |
C02 |
C03 |
| C10 |
C11 |
C12 |
C13 |
| C20 |
C21 |
C22 |
C23 |
| C30 |
C31 |
C32 |
C33 |
|
ö
÷
÷
÷
ø |
|
= |
æ
ç
ç
ç
è |
| A00 |
A01 |
A02 |
A03 |
| A11 |
A12 |
A13 |
A10 |
| A22 |
A23 |
A20 |
A21 |
| A33 |
A30 |
A31 |
A32 |
|
ö
÷
÷
÷
ø |
|
× |
æ
ç
ç
ç
è |
| B00 |
B11 |
B22 |
B33 |
| B10 |
B21 |
B32 |
B03 |
| B20 |
B31 |
B02 |
B13 |
| B30 |
B01 |
B12 |
B23 |
|
ö
÷
÷
÷
ø |
|
Puis on fait une
rotation sur A et B:
æ
ç
ç
ç
è |
| C00 |
C01 |
C02 |
C03 |
| C10 |
C11 |
C12 |
C13 |
| C20 |
C21 |
C22 |
C23 |
| C30 |
C31 |
C32 |
C33 |
|
ö
÷
÷
÷
ø |
|
= |
æ
ç
ç
ç
è |
| A01 |
A02 |
A03 |
A00 |
| A12 |
A13 |
A10 |
A11 |
| A23 |
A20 |
A21 |
A22 |
| A30 |
A31 |
A32 |
A33 |
|
ö
÷
÷
÷
ø |
|
× |
æ
ç
ç
ç
è |
| B30 |
B01 |
B12 |
B23 |
| B00 |
B11 |
B22 |
B33 |
| B10 |
B21 |
B32 |
B03 |
| B20 |
B31 |
B02 |
B13 |
|
ö
÷
÷
÷
ø |
|
10.3.2 Principe de l'algorithme de Fox
Dans cet algorithme, on ne fait pas
de mouvement de données initiales.
On effectue des diffusions horizontales des diagonales de A (décalées vers la droite
à chaque itération)
et des rotations verticales de B (de bas en haut):
/* pas de mouvements de donnees avant les calculs */
/* calcul du produit de matrices */
broadcast(A(x,x));
forall (k=1; k<sqrt(P)) {
LocalProdMat(A,B,C);
VerticalRotation(B,upwards);
broadcast(A(k+x,k+x)); }
forall () {
LocalProdMat(A,B,C);
VerticalRotation(B,upwards); }
/* pas de mouvements de donnees apres les calculs */
Par exemple, toujours pour n=4:
æ
ç
ç
ç
è |
| C00 |
C01 |
C02 |
C03 |
| C10 |
C11 |
C12 |
C13 |
| C20 |
C21 |
C22 |
C23 |
| C30 |
C31 |
C32 |
C33 |
|
ö
÷
÷
÷
ø |
|
+= |
æ
ç
ç
ç
è |
| A00 |
A00 |
A00 |
A00 |
| A11 |
A11 |
A11 |
A11 |
| A22 |
A22 |
A22 |
A22 |
| A33 |
A33 |
A33 |
A33 |
|
ö
÷
÷
÷
ø |
|
× |
æ
ç
ç
ç
è |
| B00 |
B01 |
B02 |
B03 |
| B10 |
B11 |
B12 |
B13 |
| B20 |
B21 |
B22 |
B23 |
| B30 |
B31 |
B32 |
B33 |
|
ö
÷
÷
÷
ø |
|
Puis:
æ
ç
ç
ç
è |
| C00 |
C01 |
C02 |
C03 |
| C10 |
C11 |
C12 |
C13 |
| C20 |
C21 |
C22 |
C23 |
| C30 |
C31 |
C32 |
C33 |
|
ö
÷
÷
÷
ø |
|
+= |
æ
ç
ç
ç
è |
| A01 |
A01 |
A01 |
A01 |
| A12 |
A12 |
A12 |
A12 |
| A23 |
A23 |
A23 |
A23 |
| A30 |
A30 |
A30 |
A30 |
|
ö
÷
÷
÷
ø |
|
× |
æ
ç
ç
ç
è |
| B10 |
B11 |
B12 |
B13 |
| B20 |
B21 |
B22 |
B23 |
| B30 |
B31 |
B32 |
B33 |
| B00 |
B01 |
B02 |
B03 |
|
ö
÷
÷
÷
ø |
|
10.3.3 Principe de l'algorithme de Snyder
On effectue une transposition préalable de B.
Puis, on fait à chaque étape des sommes globales sur les lignes de
processeurs (des produits calculés à chaque étape).
On accumule les résultats sur les diagonales (décalées à chaque étape vers la
droite) de C - représentées en gras dans les figures
ci-après.
Enfin, on fait des rotations verticales de B (de bas en haut, à chaque étape):
/* mouvements des donnees avant les calculs */
Transpose(B);
/* calcul du produit de matrices */
forall () {
LocalProdMat(A,B,C);
VerticalRotation(B,upwards); }
forall (k=1;k<sqrt(P)) {
GlobalSum(C(i,(i+k-1) mod sqrt(P)));
LocalProdMat(A,B,C);
VerticalRotation(B,upwards); }
GlobalSum(C(i,(i+sqrt(P)-1) mod sqrt(P)));
/* mouvements des donnees apres les calculs */
Transpose(B);
La encore, les premières étapes sont, pour n=4:
æ
ç
ç
ç
è |
| C00 |
C01 |
C02 |
C03 |
| C10 |
C11 |
C12 |
C13 |
| C20 |
C21 |
C22 |
C23 |
| C30 |
C31 |
C32 |
C33 |
|
ö
÷
÷
÷
ø |
|
+= |
æ
ç
ç
ç
è |
| A00 |
A01 |
A02 |
A03 |
| A10 |
A11 |
A12 |
A13 |
| A20 |
A21 |
A22 |
A23 |
| A30 |
A31 |
A32 |
A33 |
|
ö
÷
÷
÷
ø |
|
× |
æ
ç
ç
ç
è |
| B00 |
B01 |
B02 |
B03 |
| B10 |
B11 |
B12 |
B13 |
| B20 |
B21 |
B22 |
B23 |
| B30 |
B31 |
B32 |
B33 |
|
ö
÷
÷
÷
ø |
|
Puis:
æ
ç
ç
ç
è |
| C00 |
C01 |
C02 |
C03 |
| C10 |
C11 |
C12 |
C13 |
| C20 |
C21 |
C22 |
C23 |
| C30 |
C31 |
C32 |
C33 |
|
ö
÷
÷
÷
ø |
|
+= |
æ
ç
ç
ç
è |
| A00 |
A01 |
A02 |
A03 |
| A10 |
A11 |
A12 |
A13 |
| A20 |
A21 |
A22 |
A23 |
| A30 |
A31 |
A32 |
A33 |
|
ö
÷
÷
÷
ø |
|
× |
æ
ç
ç
ç
è |
| B10 |
B11 |
B12 |
B13 |
| B20 |
B21 |
B22 |
B23 |
| B30 |
B31 |
B32 |
B33 |
| B00 |
B01 |
B02 |
B03 |
|
ö
÷
÷
÷
ø |
|
10.4 Algorithmique hétérogène
Nous avons supposé jusqu'à présent que les différents processus parallèles
s'exécutent sur des processeurs qui ont exactement la même puissance de calcul. En général,
sur un cluster de PC, ce ne sera pas le cas: certaines seront plus rapides que d'autres. On va voir
maintenant comment faire en sorte de répartir au mieux le travail dans une telle situation.
On va considérer le problème suivant d'allocation statique de tâches. On suppose
que l'on se donne
t1,t2,...,tp les temps de cycle des processeurs, et que l'on a
B tâches identiques et indépendantes que l'on veut exécuter au mieux sur ces
p processeurs.
Le principe est que l'on va essayer d'assurer ci × ti = constante, donc on trouve:
| ci= |
ê
ê
ê
ê
ê
ê
ë |
|
ú
ú
ú
ú
ú
ú
û |
× B |
L'algorithme correspondant, qui calcule au mieux ces ci est le suivant :
Distribute(B,t1,t2,...,tn)
/* initialisation: calcule ci */
for (i=1;i<=p;i++)
c[i]=...
/* incrementer iterativement les ci minimisant le temps */
while (sum(c[])<B) {
find k in {1,...,p} st t[k]*(c[k]+1)=min{t[i]*(c[i]+1)};
c[k] = c[k]+1;
return(c[]);
On peut aussi programmer une version incrémentale de cet algorithme.
Le problème que résoud cet algorithme est plus complexe: on souhaite faire en sorte
que l'allocation soit optimale pour tout nombre d'atomes entre 1 et B.
Ceci se réalise par
programmation dynamique. Dans la suite, on donnera des exemples avec t1=3, t2=5 et t3=8.
L'algorithme est alors:
Distribute(B,t1,t2,...tp)
/* Initialisation: aucune tache a distribuer m=0 */
for (i=1;i<=p;i++) c[i]=0;
/* construit iterativement l'allocation sigma */
for (m=1;m<=B;m++)
find(k in {1,...p} st t[k]*(c[k]+1)=min{t[i]*(c[i]+1)});
c[k]=c[k]+1;
sigma[m]=k;
return(sigma[],c[]);
Par exemple, pour les valeurs de t1, t2 et t3 données plus haut, on trouve:
| # atomes |
c1 |
c2 |
c3 |
cout |
proc. sel. |
alloc. s |
| 0 |
0 |
0 |
0 |
|
1 |
|
| 1 |
1 |
0 |
0 |
3 |
2 |
s[1]=1 |
| 2 |
1 |
1 |
0 |
2.5 |
1 |
s[2]=2 |
| 3 |
2 |
1 |
0 |
2 |
3 |
s[3]=1 |
| 4 |
2 |
1 |
1 |
2 |
1 |
s[4]=3 |
| 5 |
3 |
1 |
1 |
1.8 |
2 |
s[5]=1 |
| ... |
|
|
|
|
|
|
| 9 |
5 |
3 |
1 |
1.67 |
3 |
s[9]=2 |
| 10 |
5 |
3 |
2 |
1.6 |
|
s[10]=3 |
10.4.1
LU hétérogène (1D)
A chaque étape, le processeur qui possède le bloc pivot le factorise
et le diffuse.
Les autres processeurs mettent à jour les colonnes restantes.
A l'étape suivante le bloc des b colonnes suivantes devient le
pivot.
Ainsi de suite: la taille des données passe de (n-1)× b
à (n-2)× b etc.
On a plusieurs solutions pour réaliser l'allocation statique
équilibrant les charges. On peut
redistribuer les colonnes restant à traiter à
chaque étape entre les processeurs: le problème devient alors le coût des communications.
On peut également essayer de trouver une allocation statique permettant un équilibrage de
charges à chaque étape.
On peut ainsi distribuer B tâches sur p processeurs de temps de cycle t1,
t2 etc. tp de telle manière à ce que
pour tout i Î {2,...,B}, le nombre de blocs de {i,...,B}
que possède chaque processeur Pj soit approximativement inversement
proportionnel à tj.
On alloue alors les blocs de colonnes périodiquement, dans motif de largeur B.
B est un paramètre, par exemple si la matrice est (nb)× (nb),
B=n (mais le recouvrement calcul communication est meilleur si B << n).
On utilise l'algorithme précédent en sens inverse: le bloc de colonne
1£ k £ B est alloué sur s(B-k+1).
Cette distribution est quasi-optimale pour tout sous-ensemble
[i,B] de colonnes.
Par exemple, pour
n=B=10, t1=3, t2=5, t3=8 le motif sera:
| P3 |
P2 |
P1 |
P1 |
P2 |
P1 |
P3 |
P1 |
P2 |
P1 |
10.4.2 Allocation statique 2D
Prenons l'exemple de la multiplication de matrices sur une grille homogène.
ScaLAPACK opère par un algorithme par blocs, avec une
double diffusion horizontale et verticale (comme à la figure 10.1).
Cela s'adapte au cas de matrices et de grilles. Il n'y a
aucune redistribution initiale des données.
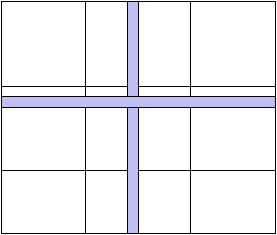
Figure 10.1: Diffusion horizontale et verticale, pour la multiplication de matrices sur une
grille homogène
Essayons d'allouer des blocs inhomogènes, mais de façon ``régulière''.
Le principe est d'allouer des rectangles de tailles différentes aux processeurs, en
fonction de leur vitesse relative. Supposons que l'on ait
p× q processeurs Pi,j de temps de cycle ti,j.
L'équilibrage de charge parfait n'est réalisable que si
la matrice des temps de cycle T=(ti,j) est
de rang 1.
Par exemple, dans la matrice de rang 2 suivante, P2,2 est partiellement inactif:
| |
1 |
|
| 1 |
t11=1 |
t12=2 |
|
t21=3 |
t22=5 |
Par contre, dans le cas d'une matrice de rang 1 comme ci-dessus, on arrive
à effectuer un équilibrage parfait:
| |
1 |
|
| 1 |
t11=1 |
t12=2 |
|
t21=3 |
t22=6 |
Le problème général revient à
optimiser:
-
Objectif Obj1:
| min |
|
maxi,j {ri × ti,j× cj} |
- Objectif Obj2:
| maxri × ti,j × cj £ 1 |
ì
í
î |
æ
ç
ç
è |
|
ri |
ö
÷
÷
ø |
× |
æ
ç
ç
è |
|
cj |
ö
÷
÷
ø |
ü
ý
þ |
De plus, l'hypothèse de régularité que nous avions faite, ne tient pas forcément.
En fait, la position des processeurs dans la grille n'est pas une donnée
du problème.
Toutes les permutations sont possibles, et il faut chercher la meilleure. Ceci nous
amène à un
problème NP-complet. En
conclusion: l'équilibrage 2D est extrêmement difficile!
10.4.3 Partitionnement libre
Comment faire par exemple avec p (premier) processeurs, comme à la figure
10.2 ?
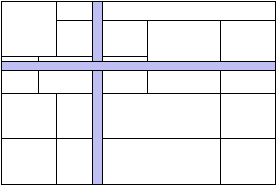
Figure 10.2: Problème de la partition libre
On suppose que l'on a
p processeurs de vitesses s1,s2,...,sn de somme 1 (normalisées).
On veut partitionner le carré unité en p rectangles de surfaces
s1,s2,...,sn.
La surface des rectangles représente la vitesse relative des processeurs.
La forme des rectangles doit permettre de minimiser les communications.
Géométriquement,
on essaie donc de partitionner le carré unité en p rectangles d'aires fixées
s1, s2, ..., sp afin de minimiser
soit la somme des demi-périmètres des rectangles dans le cas des
communications séquentielles,
soit le plus grand des demi-périmètres des rectangles dans le cas
de communications parallèles.
Ce sont deux
problèmes NP-complets.
Prenons un exemple pour bien mesurer la difficulté du partitionnement libre:
supposons que l'on ait p=5 rectangles R1,...,R5 dont les
aires sont s1=0.36, s2=0.25, s3=s4=s5=0.13 (voir figure 10.3).
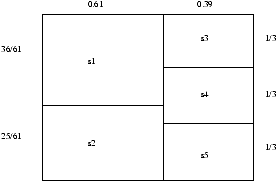
Figure 10.3: Problème de la partition libre
Alors, le
demi-périmètre maximal pour R1 est approximativement de 1.2002.
La borne inférieure absolue 2 sqrts1 = 1.2 est atteinte lorsque le
plus grand rectangle est un carré, ce qui n'est pas possible ici.
La somme des demi-périmètres est de 4.39.
La borne absolue inférieure åi=1p 2 sqrtsi=4.36 est atteinte
lorsque tous les rectangles sont des carrés.









