Parallélisme et Distribution
Eric Goubault
Commissariat à l'Energie Atomique
Le but de ce cours est de donner une idée de la programmation, algorithmique
et sémantique de systèmes parallèles et distribués.
Pour y arriver, on utilise un biais dans un premier temps, qui nous permettra d'aborder les
principaux
thèmes du domaine. On va utiliser le système de ``threads''
de JAVA pour simuler des processus parallèles et distribués.
Plus tard, on utilisera d'autres fonctionnalités de JAVA, comme les RMI, pour
effectuer véritablement des calculs en parallèle sur plusieurs machines.
Les ``threads'' en tant que tels sont une première approche du parallélisme
qui peut même aller jusqu'au ``vrai parallélisme'' sur une machine
multi-processeurs. Pour avoir un panorama un peu plus complet du parallélisme
et de la distribution, il faut être capable de faire travailler plusieurs
machines (éventuellement très éloignées l'une de l'autre; penser à
internet) en même temps. On en fera une approche, soit par simulation par
des threads, soit par le mécanisme de RMI.
Dans les sections 3.2.1 et 3.2.3, on présente d'abord le modèle
de threads de JAVA (communication par mémoire partagée) et la façon
dont on peut créer et contrôler un minimum les threads utilisateurs.
On voit un peu plus en détail
à la section 3.2.2 le fonctionnement de la JVM
en présence de threads. On donne des éléments plus avancés de contrôle
des threads JAVA à la section 3.3, en particulier en ce qui concerne
le cycle de vie des threads, les groupes de processus, les priorités, et
l'ordonnancement.
Dans le chapitre suivant on s'intéresse au très classique et important problème
de l'accès concurrent aux variables partagées. En effet la machine JVM sous-jacente
n'est pas une P-RAM CRCW mais ressemble plus à une CREW
(voir le chapitre 4 ainsi que [Rob00]).
Il faut donc faire très attention à verrouiller les accès, au moins
au moment de l'écriture comme on le verra à la section
5.1. Pour ce faire on utilisera essentiellement le mot clé
synchronized introduit à la section
5.2. On en profitera pour voir un peu de sémantique très minimaliste
dans la section
5.4.2. En effet le premier problème que l'on rencontre, et que l'on
n'a pas dans le monde séquentiel, est le problème de point mort ou
étreinte fatale (deadlock en anglais). On commence à le rencontrer
en section 5.4.2 mais ce sera toujours un thème récurrent.
A partir de synchronized on peut implémenter les mécanismes de synchronisation
et d'exclusion mutuelle typiques que l'on rencontre sous une forme ou une autre
dans tout langage parallèle. On commence par les moniteurs [Hoa74], section
5.3, puis les sémaphores binaires [Dij68], section
5.4.1 et les sémaphores plus généraux, dits à compteur,
section 5.4.5,
qui sont d'ailleurs implémentables à partir des sémaphores binaires
[Dij68]. En fait, synchronized n'est jamais qu'un sémaphore
binaire (ou verrou, ou mutex) associé à une méthode ou à un bout de code.
On en profite aussi dans la section 5.5
pour donner une implémentation des barrières de synchronisation,
très utilisées dans des programmes parallèles à gros grain, par exemple
fonctionnant sur cluster de PC.
Quand on ne veut pas mettre des barrières de synchronisation partout, mais
que l'on veut ordonnancer ces processus plus mollement (on peut alors gagner
en efficacité car l'ordonnancement a plus de degrés de liberté)
de façon à ce que l'état global
du système reste ``cohérent'' en un certain sens, on tombe sur les problèmes
classique de séquentialisation. On en donne quelques exemples, très classiques
en bases de données distribuées, et on développe
le protocole le plus connu permettant d'assurer cette cohérence dans ce cadre,
le protocole 2PL (``2-Phase Locking'') ou protocole à deux phases, en section
5.6. On se reportera au cours de S. Abiteboul, [Abi00],
pour
plus de détails et de références.
On voit enfin au chapitre 6 les grands classiques des algorithmes
permettant de programmer l'exclusion mutuelle (le synchronized) sur
des machines à mémoire partagée, sous certaines hypothèses. Cela peut
paraître assez académique mais est un excellent moyen de s'habituer à
raisonner sur des programmes parallèles se coordonnant par lecture et écriture
en mémoire partagée, et cela n'est pas si facile. Cela permet également
de se familiariser aux preuves de programmes parallèles.
Il existe des compilateurs qui parallélisent automatiquement des codes séquentiels. On en
présente les principes théoriques au chapitre 7. L'optimisation
effectuée par ces compilateurs consiste à transformer le code de telle façon à y trouver
``plus de parallélisme''.
Dans une deuxième partie, on passe du parallélisme à la distribution en partant
des architectures des machines distribuées, et des différentes topologies de communication
(chapitre 8). On voit au chapitre 9.3 comment programmer effectivement un algorithme distribué
sur un réseau de stations.
Au chapitre 10 on passe
en revue quelques algorithmes distribués classiques, permettant de faire de l'algèbre
linéaire élémentaire. C'est un bon exercice pour comprendre comment être
vraiment efficace. Il faut en particulier avoir un recouvrement optimal des calculs
et des communications, et équilibrer les charges au mieux. On verra à cette occasion
que dans un cadre hétérogène, c'est-à-dire quand les machines utilisées n'ont pas
la même puissance de calcul, il est souvent très difficile d'arriver à un équilibrage
correct.
Enfin, au chapitre 11, on complique encore un peu le jeu. Il s'agit maintenant d'écrire
des algorithmes qui en plus, sont ``tolérants aux pannes'', c'est-à-dire que même si
certains processeurs du système distribué tombent en panne en cours de calcul, les autres doivent
pouvoir terminer leur partie de calcul, de façon correcte. On a pris ici le parti
de montrer un petit bout de la théorie sous-jacente, plutôt que de parler extensivement
des algorithmes encore une fois.
Références
Pour des compléments, ou des applications du parallélisme au calcul scientifique,
on pourra se reporter à [GNS00].
Ces notes sont encore très préliminaires et on trouvera en particulier dans
[RL03] nombre de compléments. On se reportera aussi au
complément de D. Rémy [Rem00]
pour tout ce qui concerne l'orienté objet. Le livre
[Ray97] apportera au lecteur toutes les précisions voulues sur les
algorithmes vus au chapitre 6. Le lecteur trouvera enfin des compléments
sur l'algorithmique distribuée, tolérante aux pannes en particulier dans le très
encyclopédique [Lyn96]. Pour aller plus loin, en particulier en ce qui concerne la
sémantique et les modèles du parallélisme, on pourra se reporter aux notes de cours du Master
Parisien de Recherche en Informatique:
http://amanite.ens.fr/MPRI/bin/view/WebSite/C-2-3
Enfin, je remercie Matthieu Martel et Sylvie Putot d'avoir
relu ce polycopié. Les erreurs qui restent
sont néanmoins les miennes!
Ce chapitre est bien sûr loin d'être exhaustif. On n'y parle pratiquement
pas de micro-parallélisme, c'est-à-dire du parallélisme au niveau
des microprocesseurs. En effet la plupart des microprocesseurs modernes
sont à eux seuls de véritables machines parallèles. Par exemple
il n'est pas rare (Pentium, PowerPC etc.) d'avoir plusieurs unités de
calcul arithmétique (dans le cas du Pentium, d'unités de calcul
flottant, ou dans le cas des processeurs MIPS, plusieurs
additionneurs, multiplieurs etc.)
pouvant fonctionner en parallèle. On parle un peu plus
loin du calcul en pipeline qui est courant dans ce genre d'architectures.
A l'autre bout du spectre, les projets les plus
en vogue à l'heure actuelle, sont les immenses réseaux
d'ordinateurs hétérogènes distribués à l'échelle d'internet, qui posent
un certain nombre de problèmes théoriques et pratiques.
On pourra se reporter aux divers projets de ``metacomputing'',
voir par exemple
http://www.metacomputing.org/
et le projet ``GRID'', voir par exemple
http://www.gridforum.org/.
Il existe un projet de grille national (GRID'5000) pour lequel vous pouvez trouver des documents
sur le web. Il est coordonné par Franck Cappello au LRI (à l'Université d'Orsay).
2.1 Une classification des machines parallèles
Une machine parallèle est essentiellement un ensemble de processeurs
qui coopèrent et communiquent.
Historiquement, les premières machines parallèles sont
des réseaux d'ordinateurs, et des machines
vectorielles et faiblement parallèles (années 70 - IBM 360-90 vectoriel, IRIS 80 triprocesseurs, CRAY 1 vectoriel...).
On distingue classiquement quatre types principaux de parallélisme
(Taxonomie de Flynn-Tanenbaum):
SISD, SIMD, MISD et MIMD.
Cette classification est basée sur les notions de flot de contrôle (deux
premières lettres, I voulant dire ``Instruction'') et flot de
données (deux dernières lettres, D voulant dire ``Data'').
2.1.1 Machine SISD
Une machine SISD (Single Instruction Single
Data) est ce que l'on appelle d'habitude une machine séquentielle, ou
machine de Von Neuman. Une seule instruction est exécutée à un moment
donné et une seule donnée (simple, non-structurée) est traitée à
un moment donné.
Le code suivant,
int A[100];
...
for (i=1;100>i;i++)
A[i]=A[i]+A[i+1];
s'exécute sur une machine séquentielle en faisant les additions
A[1]+A[2], A[2]+ A[3], etc., A[99]+A[100] à la suite
les unes des autres.
2.1.2 Machine SIMD
Une machine SIMD (Single Instruction Multiple
Data) est une machine qui exécute à tout instant une seule instruction,
mais qui agit en parallèle sur plusieurs données, on parle en général
de ``parallélisme de données''. Les machines SIMD
peuvent être de plusieurs types, par exemple,
parallèles
ou systoliques.
Les machines systoliques sont des machines SIMD particulières dans lesquelles
le calcul se déplace sur une topologie de processeurs, comme un front d'onde,
et acquiert des données locales différentes à chaque déplacement
du front d'onde (comportant plusieurs processeurs, mais pas tous en général
comme dans le cas (1)).
En général dans les deux cas, l'exécution en parallèle de la même instruction
se fait en même temps sur des processeurs différents (parallélisme
de donnée synchrone).
Examinons par exemple le code suivant (cas (1))
écrit en
CM-Fortran sur la Connection Machine-5 avec 32 processeurs,
INTEGER I,J,A(32,1000)
CMF$ LAYOUT A(:NEWS,:SERIAL)
...
FORALL (I=1:32,J=1:1000)
$ A(I:I,J:J)=A(I:I,J:J)+A(I:I,(J+1):(J+1))
Chaque processeur i, 1 £ i £ 32
a dans sa mémoire locale une tranche du tableau
A: A(i,1), A(i,2), ..., A(i,1000). Il n'y a pas d'interférence
dans le calcul de la boucle entre les différentes tranches: tous les
processeurs exécutent la même boucle sur leur propre tranche en même
temps (cf. figure 2.1). Ceci grâce à la directive LAYOUT
qui indique à CM-Fortran que les calculs concernant la deuxième dimension
de A s'effectueront en séquentiel tandis que ceux concernant la première
dimension se feront en parallèle.
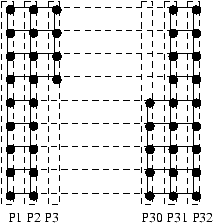
Figure 2.1: Répartion d'un tableau sur les processeurs d'une machine SIMD typique.
2.1.3 Machine MISD
Une machine MISD (Multiple Instruction Single
Data) peut exécuter plusieurs instructions en même temps
sur la même donnée. Cela peut paraître paradoxal mais cela
recouvre en fait un type très ordinaire de micro-parallélisme dans
les micro-processeurs modernes: les processeurs vectoriels et
les architectures pipelines.
Un exemple de ``pipeline'' d'une addition vectorielle est le suivant.
Considérons le code:
FOR i:=1 to n DO
R(a+b*i):=A(a'+b'*i)+B(a''+b''*i);
A, B et R sont placés dans des registres vectoriels
qui se remplissent au fur et à mesure du calcul,
| Temps |
A |
( |
i |
) |
B |
( |
i |
) |
R |
( |
i |
) |
| 1 |
1 |
. |
. |
. |
1 |
. |
. |
. |
. |
. |
. |
. |
| 2 |
2 |
1 |
. |
. |
2 |
1 |
. |
. |
. |
. |
. |
. |
| 3 |
3 |
2 |
1 |
. |
3 |
2 |
1 |
. |
. |
. |
. |
. |
| 4 |
4 |
3 |
2 |
1 |
4 |
3 |
2 |
1 |
. |
. |
. |
. |
| 5 |
5 |
4 |
3 |
2 |
5 |
4 |
3 |
2 |
1 |
. |
. |
. |
| 6 |
6 |
5 |
4 |
3 |
6 |
5 |
4 |
3 |
2 |
1 |
. |
. |
| etc. |
|
|
|
|
|
|
|
|
|
|
|
|
En ce sens, quand le pipeline est rempli, plusieurs instructions sont
exécutées sur la même donnée. Par contre, certaines instructions comme
les branchements conditionnels forcent généralement à vider le pipeline,
avant d'être exécutées. L'efficacité s'en trouve alors fortement diminuée.
2.1.4 Machine MIMD
Le cas des machines MIMD (Multiple Instruction Multiple
Data) est le plus intuitif et est celui qui va nous intéresser le
plus dans ce cours. Ici, chaque processeur peut exécuter un programme différent sur
des données différentes. On a plusieurs types d'architecture possibles:
-
(1) Mémoire partagée (Sequent etc.)
- (2) Mémoire locale + réseau de communication (Transputer, Connection
Machine) - Système réparti
C'est le cas (1) que l'on va voir plus particulièrement avec JAVA. On
pourra également simuler le cas (2). Pour le cas (2) (en PVM et
MPI) et en particulier pour
des applications au calcul scientifique, on pourra se reporter par
exemple au cours [GNS00].
Parce qu'il
n'est en général pas nécessaire d'utiliser des programmes différents pour chaque
processeur, on exécute souvent le même code sur tous les noeuds d'une machine MIMD mais ceux-ci
ne sont pas forcément synchronisés. On parle alors de modèle SPMD (Single Program Multiple
Data).
Mémoire Partagée:
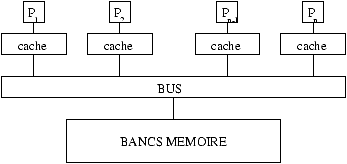
Figure 2.2: Architecture simplifiée d'une machine à mémoire partagée.
Une machine MIMD à mémoire partagée
est principalement constituée de
processeurs avec des horloges indépendantes, donc évoluant de façon asynchrone,
et communicant en écrivant et lisant des valeurs dans une seule et même
mémoire (la mémoire partagée). Une difficulté supplémentaire, que
l'on ne décrira pas plus ici,
est que chaque processeur a en général au moins un cache
de données (voir figure 2.2),
tous ces caches devant avoir des informations cohérentes aux moments
cruciaux.
La synchronisation des exécutions des processeurs (ou processus, qui en
est une ``abstraction logique'') est nécessaire dans certains
cas. Si elle n'était pas faite, il y aurait un risque d'incohérence des
données.
Partant de x=0, exécutons x:=x+x en parallèle avec x:=1.
On a alors essentiellement
quatre exécutions possibles (en supposant chacune des affectations
compilées en instructions élémentaires insécables, ou ``atomiques''), comme
suit:
| LOAD x,R1 |
WRITE x,1 |
LOAD x,R1 |
LOAD x,R1 |
| LOAD x,R2 |
LOAD x,R1 |
WRITE x,1 |
LOAD x,R2 |
| WRITE x,1 |
LOAD x,R2 |
LOAD x,R2 |
WRITE x,R1+R2 |
| WRITE x,R1+R2 |
WRITE x,R1+R2 |
WRITE x,R1+R2 |
WRITE x,1 |
| Résultat x=0 |
Résultat x=2 |
Résultat x=1 |
Résultat x=1 |
Cela n'est évidemment pas très satisfaisant; il faut rajouter des synchronisations
pour choisir tel ou tel comportement. Cela est en particulier traité
à la section 5.6.
La synchronisation peut se faire par différents mécanismes:
-
Barrières de synchronisation (voir section 5.5),
- Sémaphores : deux opérations P et V (voir section 5.4),
- Verrou (mutex lock) : sémaphore binaire qui sert à
protéger une section critique (voir section 5.4.1),
- Moniteurs : construction de haut niveau, verrou implicite (voir section 5.3),
- etc.
Les opérations P et V sur les sémaphores sont parmi les plus classiques
et élémentaires (on les verra par la suite en long, en large et en travers,
en particulier à la section 5.4).
On peut considérer qu'à chaque variable partagée x dans
la mémoire est associé un ``verrou'' (du même nom) indiquant
si un processus est en train de la manipuler, et ainsi en interdisant l'accès
pendant ce temps. L'opération Px exécutée par un processus verrouille
ainsi son accès exclusif à x. L'opération Vx ouvre le verrou et
permet à d'autres processus de manipuler x à leur tour.
La encore des erreurs sont possibles, en voulant trop synchroniser par exemple.
Il peut y avoir des cas d'interblocage (deadlock, livelock) en particulier.
Supposons qu'un processus T1 ait besoin (pour effectuer un calcul
donné) de verrouiller puis déverrouiller
deux variables x et y dans l'ordre suivant:
P x puis P y puis Vx puis Vy alors qu'un autre processus, en parallèle,
désire faire la séquence P y, P x puis V y et enfin Vx. En fait
les deux processus peuvent s'interbloquer l'un l'autre si T1 acquiert
x (respectivement T2 acquiert y) puis attend y (respectivement x).
Tout cela sera encore traité à la section 5.4.2.
Mémoire distribuée
L'emploi d'autres mécanismes de communication
que la mémoire partagée
pour une machine MIMD est dû à plusieurs choses: par exemple, les processeurs peuvent
être physiquement
trop éloignés pour qu'un partage de petites quantités d'information soit raisonnable,
par exemple, le réseau Internet permet de considérer en un certain sens,
tous les ordinateurs reliés comme étant un seul et même ordinateur
distribué, où les processeurs travaillent de façon asynchrone et
où les informations transitent par passage de message. Un
certain nombre de super-calculateurs travaillent par
échange de messages également car il n'est techniquement pas possible de connecter un
très grand nombre de processeurs directement à une même mémoire.
De façon générale, la synchronisation et l'échange d'information
peuvent se faire par,
-
Appel de procédure à distance (RPC) :
-
réponse synchrone
- réponse asynchrone
- Envoi/Réception de message asynchrone (tampon de taille limitée ou non), point à point, ou vers des groupes
de processus; par active
polling ou gestion à l'arrivée par une procédure handler. L'``active polling'' ou attente active
désigne la façon qu'un processus attendant un message a de demander périodiquement si celui-ci est arrivé,
pour effectuer son traitement. C'est une méthode consommatrice de CPU, qui n'est donc pas très efficace. La plupart
des primitives de communication asynchrones offrent la possibilité d'appeler directement une fonction utilisateur
``handler'' à l'arrivée d'un message, ce qui permet au processus demandeur d'effectuer d'autres opérations, avant
d'être interrompu par l'appel à ce ``handler'' de communication.
- Envoi/Réception de message synchrone : rendez-vous. Le modèle synchrone ou bloquant est le plus simple, et
nous verrons dans le TD 6 un modèle théorique particulièrement adapté au raisonnement dans ce cas, il s'agit
de l'algèbre de processus CCS, sorte de langage jouet décrivant les coordinations possibles de processus.
- Mélange des deux derniers cas.
Le protocole RPC (``Remote Procedure Call'') entre machines UNIX avec
réseau Ethernet est un exemple de programmation MIMD (cf. figure 2.3).
On verra au chapitre 9.3 la programmation correspondante en JAVA (à travers les RMI).
2cm
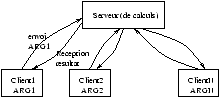
Figure 2.3: Architecture Client/Serveur (RPC).
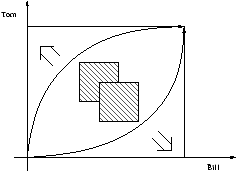
2.1.5 Gain d'efficacité
Les architectures sont plus ou moins bien adaptées à certains problèmes.
En fait, le gain de temps espéré, qui est d'au plus N (nombre de
processeurs) est rarement atteint et,
en pratique, le parallélisme est difficile à contrôler.
Enfin, pour revenir à notre première remarque sur la taxonomie de Tanenbaum,
il y a de plus en plus rarement une distinction tranchée entre le modèle
mémoire partagée et celui par passage de messages; dans la réalité, la
situation est très hybride.
2.2 Contrôle d'une machine parallèle
Il y a deux méthodes principales,
-
(1) On dispose d'un language séquentiel: le compilateur parallélise
(Fortran...),
- (2) On a une extension d'un langage séquentiel (par exemple, PVM, MPI) ou un langage dédié
avec des constructions parallèles explicites (Parallel C, Occam...)
On pourra se reporter à [Rob00] et [GNS00] pour
les techniques utilisées par les compilateurs
dans le cas (1). On en traitera un petit aspect au chapitre 7.
On se concentre ici principalement sur le deuxième cas. Il faut alors
disposer de primitives (ou instructions) pour:
-
La création de parallélisme,
-
Itération simultanée sur tous les processeurs
(FOR parallèle de Fortran ou FORALL),
- Définition d'un ensemble de processus (COBEGIN),
- Création de processus (FORK de Unix).
- Contrôler les tâches parallèles,
-
Synchronisation (Rendez-vous d'Ada),
- Passage de messages (synchrones/asynchrones,
broadcast,...),
- Sections critiques (gestion de la mémoire partagée),
- Arrêt d'une exécution parallèle (COEND, WAIT
d'Unix).
3.1 Introduction aux threads
Les ``threads'' ou ``processus légers'' sont des unités d'exécution autonomes
qui peuvent effectuer des tâches, en parallèle avec d'autres threads:
ils sont constitués d'un identificateur, d'un compteur de programme, d'une pile
et d'un ensemble de variables locales. Le flot de contrôle d'un thread est donc purement
séquentiel. Plusieurs threads peuvent être associés à un ``processus lourd''
(qui possède donc un flot de contrôle multiple, ou parallèle). Tous les
threads associés à un processus lourd ont en commun un certain nombre de ressources,
telles que: une partie du code à exécuter, une partie des données, des fichiers
ouverts et des signaux.
En Java, le processus lourd sera la JVM (Java Virtual Machine) qui interprète
le bytecode des différents processus légers. Les threads coopèrent entre
eux en échangeant des valeurs par la mémoire commune (du processus lourd).
On en verra à la section 5.1 la sémantique
détaillée.
L'intérêt d'un système ``multi-threadé'', même sur une machine monoprocesseur,
est que l'ordinateur donne l'impression d'effectuer plusieurs tâches en parallèle.
Les systèmes d'exploitation modernes (Linux, Windows XP, MacOS X etc.)
sont tous multi-threadés contrairement aux premiers OS de micro-ordinateurs. Le fait de
pouvoir ouvrir en même temps netscape, emacs, et un shell par exemple,
et de pouvoir passer d'une fenêtre à l'autre sans attente est la marque
d'un tel système. L'application netscape même est multi-threadée.
Une tâche essaie de se connecter au site choisi, pendant qu'une autre imprime
à l'écran etc. Imaginez ce que ce serait si vous ne voyiez rien à l'écran
tant que le site auquel vous vous connectez n'a pas fini de vous transmettre toutes
les données!
En fait, un système d'exploitation comme Unix comporte des processus (lourds)
multiples, tels les démons systèmes (ou processus noyau) et souvent un
grand nombre de processus (lourds) utilisateurs. Il n'est pas rare d'avoir quelques
dizaines voire une centaine de processus lourds sur une machine à tout instant (faire
ps -al par exemple).
Sur une machine multiprocesseur, des threads peuvent être exécutés sur
plusieurs processeurs donc réellement en même temps, quand le système
d'exploitation et le support pour les threads sont étudiés pour (c'est
le cas pour Windows NT, Solaris 2, Linux etc.). Pour rentrer un peu plus dans
les détails, les threads que nous programmerons sont des ``threads utilisateurs''
qui doivent communiquer avec le noyau de système d'exploitation de temps en
temps, ne serait-ce que pour imprimer à l'écran, lire et écrire des
fichiers etc. Tout thread utilisateur doit donc être lié d'une façon ou
d'une autre à un thread ``noyau''. Selon les implémentations, chaque tâche
utilisateur peut être liée à une tâche noyau, ou plusieurs tâches utilisateur à
plusieurs tâches noyaux, ou encore plusieurs tâches
utilisateur à une tâche noyau. La première version de Solaris (``green threads'')
implémentait
seulement la dernière possibilité qui est la seule qui ne permet pas de bénéficier de vrai parallélisme sur une architecture multiprocesseur.
A partir de Java 1.1 et pour les versions plus récentes de Solaris et de Linux,
on est dans le deuxième cas, qui offre le plus de flexibilité et de performances.
3.2 Les threads en JAVA
Les threads (ou processus légers) sont définis dans le langage
JAVA, et ne sont pas comme en C ou C++, une extension que l'on peut
trouver dans différentes bibliothèques.
Pour créer un thread, on crée une instance de la classe Thread,
Thread Proc = new Thread();
Une fois créé, on peut configurer Proc, par exemple lui associer
une priorité (on en parlera plus à la section 3.3.1). On pourra
ensuite l'exécuter en invoquant sa méthode start. Cette méthode va
à son tour invoquer la méthode run du thread. Comme la méthode
run de la classe Thread ne fait rien, il faut la surcharger.
C'est possible par exemple si on définit Proc comme une
instance d'une sous-classe de Thread, dans laquelle on redéfinit
la méthode run.
En général
on a envie qu'un processus contienne des données locales, donc il
est vraiment naturel de définir un processus comme une instance d'une
sous-classe de Thread en général, voir par exemple la figure 3.1
class Compte extends Thread {
int valeur;
Compte(int val) {
valeur = val;
}
public void run() {
try {
for (;;) {
System.out.print(valeur + " ");
sleep(100);
}
} catch (InterruptedException e) {
return;
}
}
public static void main(String[] args) {
new Compte(1).start();
new Compte(2000).start();
}
}
|
Figure 3.1: Classe Compte programmée par extension de la classe Thread.
La classe Compte gère uniquement ici un entier représentant
une somme d'un compte courant d'une banque. Après avoir défini le
constructeur, on a écrit une méthode run qui sera exécutée
deux fois par deux instances différentes de la classe à partir
du main, l'une avec une valeur de compte initiale égale
à 1 et l'autre, à 2000. La méthode run se contente d'afficher
la valeur courante du compte tous les dixièmes de seconde, jusqu'à
une interruption clavier.
L'exécution du programme main donne quelque chose comme,
> java Compte
1 2000 1 2000 1 1 2000 1
^C
>
Néanmoins, cette méthode de création de thread n'est pas toujours acceptable. En effet
dans certains cas, on veut étendre une classe existante et en faire
une sous-classe de Thread également, pour pouvoir exécuter ses
instances en parallèle. Le problème est qu'il n'y a pas d'héritage
multiple en JAVA (c'est d'ailleurs plutôt un bien, car c'est en général très
difficile à contrôler, voir C++). Donc on ne peut pas utiliser
la méthode précédente. A ce moment là on utilise l'interface
Runnable.
L'interface Runnable représente du code exécutable, et ne possède
qu'une méthode,
public void run();
Par exemple la classe Thread implémente l'interface
Runnable. Mieux encore, on peut construire une instance
de Thread à partir d'un objet qui implémente l'interface
Runnable par le constructeur:
public Thread(Runnable target);
On peut écrire à nouveau la classe Compte comme à la figure 3.2.
La seule différence visible est à la création des threads Compte. Il faut en effet
utiliser le constructeur décrit plus haut avant d'appeler la méthode start.
Une dernière remarque pour ce bref rappel sur la création des threads. Il ne faut surtout pas
appeler directement la méthode run pour lancer un processus: le comportement du programme
serait tout à fait incompréhensible.
class Compte implements Runnable {
int valeur;
Compte(int val) {
valeur = val;
}
public void run() {
try {
for (;;) {
System.out.print(valeur + " ");
sleep(100);
}
} catch (InterruptedException e) {
return;
}
}
public static void main(String[] args) {
Runnable compte1 = new Compte(1);
Runnable compte2 = new Compte(2000);
new Thread(compte1).start();
new Thread(compte2).start();
}
}
|
Figure 3.2: Classe Compte programmée par implémentation de l'interface Runnable.
3.2.2 Partage des variables
Sur l'exemple de la section précédente il faut noter plusieurs choses.
Les entiers valeur sont distincts dans les deux threads qui
s'exécutent. C'est une variable locale au thread.
Si on avait déclaré static int valeur, cette variable
aurait été partagée par ces deux threads.
En fait, il aurait été même préférable de déclarer
static volatile int valeur afin de ne pas avoir des optimisations
gênantes de la part de javac...
Si on avait déclaré Integer valeur (``classe enveloppante''
de int) ou UnEntier valeur,
comme à la figure 3.3, cette classe, utilisée en lieu et place de int aurait pu être partagée par tous les
threads, car une instance de classe, comme dans ce cas, n'est qu'un pointeur vers la mémoire
partagée.
public class UnEntier {
int val;
public UnEntier(int x) {
val = x;
}
public int intValue() {
return val;
}
public void setValue(int x) {
val = x;
}
}
|
Figure 3.3: La classe UnEntier.
3.2.3 Quelques fonctions élémentaires sur les threads
Pour s'amuser (disons que c'est au moins utile pour débugger) on
peut nommer les threads:
void setName(String name) nomme le thread courant.
String getName() renvoie le nom du thread.
Un peu plus utile maintenant: on peut recueillir un certain nombre
d'informations sur les threads présents à l'exécution. Par exemple,
static Thread currentThread() renvoie la référence au thread courant
c'est-à-dire celui qui exécute currentThread().
La méthode
int enumerate(Thread[] threadArray)
place tous les threads existants
(y compris le main() mais pas le thread ramasse-miettes) dans le tableau threadArray et renvoie leur nombre.
static int activeCount() renvoie le nombre de threads actifs (on définira mieux ce que cela peut être aux sections
suivantes).
Voici un petit exemple d'utilisation (que l'on pourra également trouver, comme
tous les autres exemples de ce cours, sur la page web du cours
http://www.enseignement.polytechnique.fr/profs/informatique/Eric.Goubault/ParaI05.html), à la figure
3.4.
class Compte3 extends Thread {
int valeur;
Compte3(int val) {
valeur = val;
}
public void run() {
try {
for (;;) {
System.out.print(valeur + " ");
sleep(100);
}
} catch (InterruptedException e) {
return; } }
public static void printThreads() {
Thread[] ta = new Thread[Thread.activeCount()];
int n = Thread.enumerate(ta);
for (int i=0; i<n; i++) {
System.out.println("Le thread "+ i + " est
" + ta[i].getName());
} }
public static void main(String[] args) {
new Compte3(1).start();
new Compte3(2000).start();
printThreads(); } }
|
Figure 3.4: Nouvelle implémentation de la classe Compte.
Son exécution donne:
% java Compte3
1 2000 Le thread 0 est main
Le thread 1 est Thread-2
Le thread 2 est Thread-3
1 2000 1 2000 1 2000 1 2000 2000
1 1 2000 2000 1 1 2000 2000 1 1
2000 2000 1 1 2000 2000 1 1 2000
2000 1 1 2000 2000 1 1 ^C
%
3.3 Eléments avancés
Pour commencer cette section, il faut d'abord expliquer quels peuvent être
les différents états des threads JAVA. Un thread peut être dans l'un
des 4 cas suivants:
-
l'état initial, comprenant tous les instants entre sa création (par
un constructeur) et l'invocation de sa méthode start().
- l'état prêt, immédiatement après que la méthode start
ait été appelée.
- l'état bloqué représentant les instants où le thread est
en attente, par exemple d'un verrou, d'un socket, et également quand
il est suspendu (par la méthode sleep(long) qui suspend l'exécution
du thread pendant un certain temps exprimé en nanosecondes, ou suspend).
On repasse à l'état prêt (ou exécution) quand le verrou est de nouveau disponible, ou quand
a été fait resume, notify etc.
- l'état terminaison, quand sa méthode run() se termine ou
quand on invoque la méthode stop() (à éviter si possible, d'ailleurs
cette méthode n'existe plus en JAVA 2).
On peut déterminer l'état d'un thread en appelant sa méthode
isAlive(), qui renvoie un booléen indiquant si un thread est encore
vivant, c'est-à-dire s'il est prêt ou bloqué.
On peut aussi interrompre l'exécution d'un thread qui est prêt (passant
ainsi dans l'état bloqué).
void interrupt() envoie une interruption au thread spécifié;
si l'interruption se produit dans une méthode sleep, wait ou
join (que l'on va voir plus tard),
elles lèvent une exception InterruptedException1; sinon
le thread cible doit utiliser une des méthodes suivantes pour savoir si il
a été interrompu:
static boolean interrupted() renvoie un booléen disant si le
thread courant a été ``interrompu'' par un autre ou pas et l'interrompt,
boolean isInterrupted() renvoie un booléen disant si le thread
spécifié a été interrompu ou pas (sans rien faire d'autre).
La méthode void join() (comme sous Unix) attend la terminaison d'un thread.
Egalement: join(long timeout) attend au maximum timeout
millisecondes.
Voir par exemple la figure 3.5: la méthode stop ainsi définie bloque jusqu'à ce que
le processus identifié par t ait terminé son exécution. C'est une méthode de synchronisation
particulièrement utile dans la pratique, et que l'on verra souvent en TD.
public class ... extends Thread {
...
public void stop() {
t.shouldRun=false;
try {
t.join();
} catch (InterruptedException e) {} } }
|
Figure 3.5: Utilisation typique de join.
On peut affecter à chaque processus une priorité, qui est un nombre entier. Plus
ce nombre est grand, plus le processus est prioritaire.
void setPriority(int priority) assigne une priorité au thread donné et
int getPriority() renvoie la priorité d'un thread donné.
L'idée est que plus un processus est prioritaire, plus l'ordonnanceur JAVA
doit lui permettre de s'exécuter tôt et vite.
La priorité peut être maximale: Thread.MAX_PRIORITY (en général 10), normale (par défaut):
Thread.NORM_PRIORITY (en général 5), ou minimale Thread.MIN_PRIORITY (elle vaut en
général 0).
Pour bien comprendre cela,
il nous faut décrire un peu en détail la façon dont sont ordonnancés
les threads JAVA. C'est l'objet de la section suivante.
On peut également déclarer un processus comme étant un démon ou
pas:
setDaemon(Boolean on);
boolean isDaemon();
La méthode setDaemon doit être appelée sur un processus avant qu'il soit lancé (par
start).
Un processus démon est typiquement un processus ``support'' aux autres. Il a la propriété d'être
détruit quand il n'y a plus aucun processus utilisateur (non-démon) restant
(en fait il y a un certain nombre de threads systèmes par JVM: ramasse-miettes,
horloge, etc.). En fait, il est même détruit dès que le processus l'ayant créé est détruit ou termine.
3.3.2 Ordonnancement des tâches JAVA
Le choix du thread JAVA à exécuter (au moins partiellement)
se fait parmi les threads qui sont prêts. Supposons que nous soyons
dans le cas monoprocesseur. Il y aura donc à tout moment un seul thread
actif à choisir. L'ordonnanceur JAVA est un ordonnanceur préemptif basé
sur la priorité des processus. Essayons d'expliquer ce que
cela veut dire. ``Basé sur la priorité'' veut dire qu'à tout moment,
l'ordonnanceur essaie de rendre actif le (si on se place d'abord
dans le cas simple où il n'y a pas deux threads de même priorité)
thread prêt de plus haute
priorité. ``Préemptif'' veut dire que l'ordonnanceur use de son droit
de préemption pour interrompre le thread courant de priorité moindre,
qui reste néanmoins prêt.
Il va de soit qu'un thread actif qui devient bloqué, ou qui termine rend
la main à un autre thread, actif, même s'il est de priorité moindre.
Attention tout de même, un système de priorité n'est en aucun cas une
garantie: c'est pourquoi on insiste sur le ``essaie'' dans la phrase
``l'ordonnanceur essaie de rendre actif le thread prêt de plus haute
priorité''. On verra au chapitre 6 des algorithmes
permettant d'implémenter l'exclusion mutuelle à partir de quelques
hypothèses de base, elles ne font aucunement appel aux priorités. Un système
de priorités ne peut en effet garantir des propriétés strictes comme l'exclusion
mutuelle.
Il y a maintenant plusieurs façons d'ordonnancer des threads de même
priorité. La spécification de la JVM ne définit pas cela précisément.
Il y a par exemple la méthode d'ordonnancement ``round-robin'' (ou ``tourniquet'') dans lequel
un compteur interne fait alterner l'un après l'autre (pendant des périodes
de temps prédéfinies) les processus prêts de même priorité. Cela
assure l'équité dans l'exécution de tous les processus, c'est-à-dire
que tous vont progresser de conserve, et qu'aucun ne sera en état de famine
(les processus ``plus rapides'' étant toujours ordonnancés, ne laissant pas la possibilité
aux autres d'être ordonnancés).
Un ordonnancement plus classique (mais pas équitable en général) est
celui où un thread d'une certaine priorité, actif, ne peut pas être
préempté par un thread prêt de même priorité. Il faut que celui-ci
passe en mode bloqué pour qu'un autre puisse prendre la main.
Cela peut se faire en interrompant régulièrement les processus par
des sleep() mais ce n'est pas très efficace. Il vaut mieux
utiliser static void yield(): le thread courant rend la main, ce qui permet
à la machine virtuelle JAVA de rendre actif un autre thread de même priorité.
Tout n'est pas complètement aussi simple que cela. L'ordonnancement
dépend en fait aussi bien de l'implémentation de la JVM que du système
d'exploitation sous-jacent. Il y a deux modèles principaux concernant la
JVM. Dans le modèle ``green thread'', c'est la JVM qui implémente l'ordonnancement
des threads qui lui sont associés. Dans le modèle ``threads natifs'', c'est
le système d'exploitation hôte de la JVM qui effectue l'ordonnancement
des threads JAVA.
Le modèle ``green thread'' est le plus souvent utilisé dans les systèmes UNIX
donc même sur une machine multi-processeurs, un seul thread JAVA sera exécuté
à la fois sur un tel système.
Par contre sur les plateformes Windows (Windows 95 ou Windows NT), les threads
sont des threads natifs, et les threads JAVA correspondent bijectivement à
des threads noyaux.
Sous Solaris, la situation est plus complexe, car il y a un niveau intermédiaire
de processus connu du système d'exploitation (les ``light-weight processes'').
On n'entrera pas ici dans les détails.
Pour ceux qui sont férus de système, disons que l'on peut contrôler
pas mal de choses de ce côté là grâce à la Java Native Interface,
voir par exemple
http://java.sun.com/docs/books/tutorial/native1.1/
3.3.3 Les groupes de processus
JAVA permet de définir des groupes de processus. Il existe une classe
class ThreadGroup qui représente précisément ces groupes de processus.
On peut définir un nouveau Thread dans un groupe donné
par les constructeurs,
new Thread(ThreadGroup group, Runnable target);
new Thread(ThreadGroup group, String name);
new Thread(ThreadGroup group, Runnable target, String name);
Par défaut, un thread est créé dans le groupe courant (c'est-à-dire
de celui qui l'a créé). Au démarrage, un thread est
créé dans le groupe de nom main. On peut créer de nouveaux
groupes et créer des threads appartenant à ces groupes par de
nouveaux constructeurs. Par exemple,
ThreadGroup Groupe = new ThreadGroup("Mon groupe");
Thread Processus = new Thread(Groupe, "Un processus");
...
ThreadGroup MonGroupe = Processus.getThreadGroup();
On peut également faire des sous-groupes (en fait n'importe quelle
arborescence est autorisée). On peut alors demander un certain nombre d'informations:
Groupe.getParent();
Groupe.getName();
Groupe.activeCount();
Groupe.activeGroupCount();
Groupe.enumerate(Thread[] list);
Groupe.enumerate(Thread[] list, boolean recurse);
Groupe.enumerate(ThreadGroup[] list);
Groupe.enumerate(ThreadGroup[] list, boolean recurse);
La première instruction permet de connaître le groupe parent, la deuxième
le nom du groupe (une String), la troisième
le nombre de threads du groupe Groupe, la quatrième le nombre
de groupes de threads, et les quatre suivantes, d'énumérer soit les threads
d'un groupe, soit les groupes (cela remplit le tableau correspondant à chaque
fois). Le booléen recurse indique si on désire avoir la liste récursivement,
pour chaque sous-groupe etc.
- 1
- C'est pourquoi
il faut toujours encapsuler ces appels dans un bloc try ... catch(InterruptedException e)
4.1 Introduction
Dans ce premier chapitre sur la modélisation ``théorique'' de la calculabilité et
de la complexité sur une machine parallèle, on fait un certain nombre d'hypothèses
simplificatrices, voire très peu réalistes.
Tout comme la complexité des algorithmes séquentiels suppose que ceux-ci
sont exécutés sur une machine conforme au modèle de Von Neumann, aussi
appelée
RAM pour Random Access Machine, nous avons besoin de définir un modèle
de machine parallèle ``théorique'',
pour pouvoir analyser le comportement asymptotique d'algorithmes
utilisant plusieurs unités de calcul à la fois.
Le modèle le plus répandu est la PRAM (Parallel Random Access Machine),
qui est composée:
-
d'une suite d'instructions à exécuter plus un pointeur sur
l'instruction courante,
- d'une suite non bornée de processeurs parallèles,
- d'une mémoire partagée par l'ensemble des processeurs.
La PRAM ne possédant qu'une seule mémoire et qu'un seul pointeur de
programme,
tous les processeurs exécutent la même opération au même moment.
Supposons que nous voulions modéliser ce qui se passe sur une machine parallèle dont
les processeurs peuvent communiquer entre eux à travers une mémoire partagée.
On va tout d'abord supposer que l'on a accès à un nombre éventuellement infini de
processeurs.
Maintenant, comment
modéliser le coût d'accès à une case mémoire? Quel est le coût d'un accès
simultané de plusieurs processeurs à la mémoire partagée? L'hypothèse que l'on
va faire est que le coût d'accès de n'importe quel nombre de processeurs à n'importe
quel sous-ensemble de la mémoire, est d'une unité. On va aussi se permettre de faire trois
types d'hypothèses sur les accès simultanés à une même case mémoire:
-
EREW (Exclusive Read Exclusive Write): seul un processeur peut lire et écrire à un moment
donné sur une case donnée de la mémoire partagée.
- CREW (Concurrent Read Exclusive Write): plusieurs processeurs peuvent lire en même temps
une même case, par contre, un seul à la fois peut y écrire.
C'est un modèle proche des machines
réelles (et de ce que l'on a vu à propos des threads JAVA).
- CRCW (Concurrent Read Concurrent Write): c'est un modèle étonnament puissant et assez
peu réaliste, mais qu'il est intéressant de considérer d'un point de vue théorique.
Plusieurs processeurs peuvent lire ou écrire en même temps sur la même case de la
mémoire partagée. Il nous reste à définir ce qui se passe lorsque plusieurs processeurs
écrivent au même moment; on fait généralement l'une des trois hypothèses suivantes:
-
mode consistant: tous les processeurs qui écrivent en même temps sur la même case
écrivent la même valeur.
- mode arbitraire: c'est la valeur du dernier processeur qui écrit qui est prise en compte.
- mode fusion: une fonction associative (définie au niveau de la mémoire), est appliquée
à toutes les écritures simultanées sur une case donnée. Ce peut être par exemple,
une fonction maximum, un ou bit à bit etc.
Les algorithmes que nous allons développer dans les sections suivantes seront déclarés être des algorithmes
EREW, CREW ou CRCW si nous pouvons les écrire de telle façon qu'ils respectent les
hypothèses de ces différents modes de fonctionnement.
4.2 Technique de saut de pointeur
Ceci est la première technique importante sur les machines PRAM. On l'illustre
dans le cas assez général où l'on souhaite calculer le résultat d'une opération
binaire associative Ä
sur un n-uplet. Soit donc (x1,...,xn) une suite
(en général de nombres). Il s'agit de calculer la suite (y1,...,yn) définie
par y1=x1 et, pour 1 £ k £ n, par
yk=yk-1 Ä xk
Pour résoudre ce problème on choisit une PRAM avec n processeurs. Remarquez ici que le
nombre de processeurs dépend du nombre de données!
L'opérateur binaire associatif que l'on utilise sera représenté par op.
Chaque valeur xi et yi est représentée par une
variable partagée x[i] et y[i], qui va être gérée par le processeur Pi.
On représente le n-uplet
(x1,...,xn) par une liste chaînée, avec la case pointée par next[i]
qui contient x[i+1] pour
i < n et next[n]=nil.
On obtient alors l'algorithme suivant:
for each processor i in parallel {
y[i] = x[i];
}
while (exists object i s.t. next[i] not nil) {
for each processor i in parallel {
if (next[i] not nil) {
y[next[i]] =_next[i] op_next[i](y[i],y[next[i]]);
next[i] =_i next[next[i]];
}
}
}
On a pris les notations (que l'on utilisera rarement, car elles sont lourdes):
-
op_j pour préciser que l'opération op s'effectue sur le processeur j.
- =_j pour préciser que l'affectation est faite par le processeur j.
Notons [i,j]=xi Ä xi+1 Ä ... Ä xj pour i < j. Les quatre étapes
nécessaires au calcul, pour n=6 sont représentées à la figure 4.1. On note
qu'à la fin, tous les next[i] valent nil.
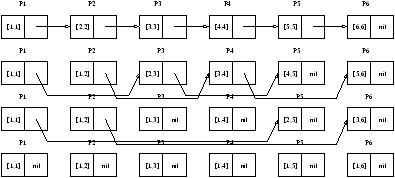
Figure 4.1: Technique du saut de pointeur.
Le principe de l'algorithme est simple: à chaque étape de la boucle, les listes courantes sont
dédoublées en des listes des objets en position paire, et des objets en position impaire.
C'est le même principe que le ``diviser pour régner'' classique en algorithmique séquentielle.
Remarquez que si on avait écrit
y[i] =_i op_i(y[i],y[next[i]]);
à la place de
y[next[i]] =_next[i] op_next[i](y[i],y[next[i]]);
on aurait obtenu l'ensemble des préfixes dans l'ordre inverse, c'est-à-dire que P1 aurait
contenu le produit [1,6], P2 [1,5], jusqu'à P6 qui aurait calculé [6,6].
Il y a tout de même une petite difficulté: nous avons parlé d'étapes, et il est vrai
que la seule exécution qui nous intéresse, et qui est correcte, est celle où chacun des
processeurs est d'une certaine façon synchronisé: chacun en est au même déroulement
de boucle à tout moment. C'est la sémantique du for parallèle
que nous choisirons pour la suite. De plus une boucle parallèle du style:
for each processor i in parallel
A[i] = B[i];
a en fait exactement la même sémantique que le code suivant:
for each processor i in parallel
temp[i] = B[i];
for each processor i in parallel
A[i] = temp[i];
dans lequel on commence par effectuer les lectures en parallèle, puis, dans un
deuxième temps, les écritures parallèles.
Il y a clairement ë log(n) û itérations dans l'algorithme du saut de pointeur, pour le
calcul du produit d'une suite de nombre, et on obtient facilement un algorithme
CREW en temps logarithmique. Il se trouve que l'on obtient la même complexité dans le
cas EREW, cela en transformant simplement les affectations dans la boucle, en passant par
un tableau temporaire:
d[i] = d[i]+d[next[i]];
devient:
temp[i] = d[next[i]];
d[i] = d[i]+temp[i];
Supposons que l'opération associative dans notre cas soit la somme. Voici un exemple d'implémentation
de cette technique de saut de pointeurs avec des threads JAVA.
On dispose d'un tableau t contenant n éléments de type int. Ici on s'est contenté
de donner le code pour le cas n=8.
On souhaite écrire un programme calculant les sommes partielles des éléments de t.
Pour cela, on crée n threads, le thread p étant chargé de calculer
åi=0i=p-1t[i].
public class SommePartielle extends Thread {
int pos,i;
int t[][];
SommePartielle(int position,int tab[][]) {
pos = position;
t=tab;
}
public void run() {
int i,j;
for (i=1;i<=3;i++) {
j = pos-Math.pow(2,i-1);
if (j>=0) {
while (t[j][i-1]==0) {} ; // attendre que le resultat soit pret
t[pos][i] = t[pos][i-1]+t[j][i-1] ;
} else {
t[pos][i] = t[pos][i-1] ;
};
};
}
}
L'idée est que le résultat de chacune des 3=log2(n) étapes, disons l'étape i, du saut de pointeur se trouve
en t[proc][i] (proc étant le numéro du processeur concerné, entre 0 et 8).
Au départ, on initialise (par l'appel au constructeur SommePartielle) les valeurs que voient
chaque processeur: t[proc][0]. Le code ci-dessous initialise le tableau d'origine de façon aléatoire,
puis appelle le calcul parallèle de la réduction par saut de pointeur:
import java.util.* ;
public class Exo3 {
public static void main(String[] args) {
int[][] tableau = new int[8][4];
int i,j;
Random r = new Random();
for (i=0;i<8;i++) {
tableau[i][0] = r.nextInt(8)+1 ;
for (j=1;j<4;j++) {
tableau[i][j]=0;
};
};
for (i=0;i<8;i++) {
new SommePartielle(i,tableau).start() ;
};
for (i=0;i<8;i++) {
while (tableau[i][3]==0) {} ;
};
for (i=0;i<4;i++) {
System.out.print("\n");
for (j=0;j<8;j++) {
System.out.print(tableau[j][i]+" ");
};
};
System.out.print("\n");
}
}
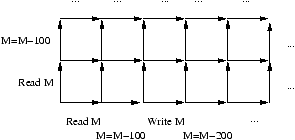
4.3 Circuit Eulerien
On souhaite calculer à l'aide d'une machine PRAM EREW la profondeur de tous les
noeuds d'un arbre binaire. C'est l'extension naturelle du problème de la section précédente,
pour la fonction ``profondeur'', sur une structure de données plus complexe que les listes.
On suppose qu'un arbre binaire est représenté par un type
abstrait arbre_binaire contenant les champs suivants :
-
int numero : numéro unique associé à chaque noeud,
- int profondeur : valeur à calculer,
- arbre_binaire pere : père du noeud courant de l'arbre,
- arbre_binaire fg,fd : fils gauche et droit du noeud courant dans l'arbre.
Un algorithme séquentiel effectuerait un parcours en largeur d'abord,
et la complexité dans le pire cas serait de O(n) où
n est le nombre de noeuds de l'arbre.
Une première façon de paralléliser cet algorithme consiste à propager une ``vague''
de la racine de l'arbre vers ses feuilles. Cette vague atteint tous les noeuds de même
profondeur au même moment et leur affecte la valeur d'un compteur correspondant à la profondeur actuelle.
Un pseudo-code serait (où le forall indique une boucle for effectuée en parallèle):
actif[0] = true;
continue = true;
p = 0; /* p est la profondeur courante */
forall j in [1,n-1]
actif[j] = false;
while (continue == true)
forall j in [0,n-1] such that (actif[j] == true) {
continue = false;
prof[j] = p;
actif[j] = false;
if (fg[j] != nil) {
actif[fg[j]] = true;
continue = true;
p++; }
if (fd[j] != nil) {
actif[fd[j]] = true;
continue = true;
p++; }
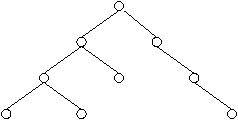
Figure 4.2:
Un arbre binaire assez quelconque.
La complexité de ce premier algorithme est de O(log(n)) pour les arbres équilibrés,
O(n) dans le cas le pire (arbres
``déséquilibrés'') sur une PRAM CRCW.
Nous souhaitons maintenant écrire un second algorithme dont la complexité est meilleure que la précédente.
Tout d'abord, nous rappelons qu'un circuit Eulerien d'un graphe orienté G est un circuit passant une et une seule fois
par chaque arc de G. Les sommets peuvent être visités plusieurs fois lors du parcours.
Un graphe orienté G possède un circuit Eulerien si et seulement si le degré entrant de chaque noeud v
est égal à son degré sortant.
Il est possible d'associer un cycle Eulerien à tout arbre binaire dans lequel on remplace les
arêtes par deux arcs orientés de sens opposés,
car alors
le degré entrant est alors trivialement égal au degré sortant.
Remarquons que dans un arbre binaire, le degré (total) d'un noeud est d'au plus 3. Dans un circuit eulérien, tout arc
est pris une unique fois, donc on passe au plus 3 fois par un noeud.
Nous associons maintenant 3 processeurs d'une machine PRAM, Ai, Bi et Ci,
à chaque noeud i de l'arbre. On suppose que chacun des 3n processeurs possède deux variables
successeur et poids. Les poids sont des valeurs entières égales à -1 (pour Ci), 0
(pour Bi) et 1 (pour Ai).
Il est alors possible de définir un chemin reliant tous les processeurs et tel que la somme des
poids rencontrés sur un chemin allant de la source à un noeud Ci soit égale à la profondeur
du noeud i dans l'arbre initial.
En effet, il est clair que la visite d'un sous-arbre à partir d'un noeud se fait par un chemin de poids nul (car
on repasse à chaque fois par un -1, 0 et un 1, de somme nulle). Donc le poids d'un noeud est égal à la
somme des poids associés aux processeurs Ai, c'est-à-dire à la profondeur.
Pour obtenir un algorithme pour PRAM EREW permettant de calculer le chemin précédent, il s'agit d'initialiser
les champs successeur et poids de chaque processeur à l'aide de l'arbre initial.
On suppose pour simplifier que les noeuds sont identifiés à leur numéro et que
pere, fg et fd sont des fonctions qui à un numéro associent un numéro.
On suppose également que les processeurs Ai ont pour numéro 3i, les Bi ont pour numéro 3i+1, et les
Ci ont pour numéro 3i+2. Alors on définit:
-
successeur[3i] = 3fg[i] si fg[i] est différent de null et
successeur[3i] = 3i+1 sinon.
- successeur[3i+1] = 3fd[i] si fd[i] est différent de null et
successeur[3i+1] = 3i+2 sinon.
- successeur[3i+2] = 3pere[i]+2
Tout ceci se fait en temps constant.
A partir de l'initialisation des champs effectuée comme précédemment, il suffit d'utiliser la
technique de saut de pointeur vue à la section 4.2
sur le parcours des 3n processus Ai, Bi et Ci.
Tout ceci se fait donc en O(log(n)).
4.4 Théorèmes de simulation
Dans ce paragraphe, nous discutons de la puissance comparée des machines CRCW, CREW et EREW.
Tout d'abord, remarquons que l'on peut trivialiser certains calculs sur une CRCW. Supposons
que l'on souhaite calculer le maximum d'un tableau A à n éléments sur une
machine CRCW à n2 processeurs. En fait chaque processeur va contenir un couple de
valeurs A[i], A[j] plus d'autres variables intermédiaires.
Le programme est alors le suivant:
for each i from 1 to n in parallel
m[i] = TRUE;
for each i, j from 1 to n in parallel
if (A[i] < A[j])
m[i] = FALSE;
for each i from 1 to n in parallel
if (m[i] == TRUE)
max = A[i];
La PRAM considérée fonctionne en mode CRCW en mode consistant, car tous les processeurs qui
peuvent écrire en même temps sur une case (en l'occurence un m[i]) ne peuvent
écrire que FALSE.
On constate que l'on arrive ainsi à calculer le maximum en temps constant sur une CRCW, alors
qu'en fait, on n'avait pu faire mieux que ë log(n) û dans le cas d'une CREW, et
même d'une EREW.
Pour séparer une CREW d'une EREW, il existe un problème simple. Supposons que l'on dispose
d'un n-uplet (e1,...,en) de nombres tous distincts, et que l'on cherche si un
nombre donné e est l'un de ces ei. Sur une machine CREW, on a un programme qui résout
ce problème en temps constant, en effectuant chaque comparaison avec un ei sur des processeurs distincts (donc
n processeurs en tout):
res = FALSE;
for each i in parallel {
if (e == e[i])
res = TRUE;
Comme tous les ei sont distincts, il ne peut y avoir qu'un processeur qui essaie d'écrire sur
res, par contre, on utilise ici bien évidemment le fait que tous les processeurs peuvent
lire e en même temps.
Sur une PRAM EREW, il faut dupliquer la valeur de e sur tous les processeurs. Ceci ne peut se
faire en un temps meilleur que log(n), par dichotomie. Ceci vaut également pour l'écriture concurrente.
On va maintenant voir que ce facteur
est un résultat général.
Théorème
Tout algorithme sur une machine PRAM CRCW (en mode consistant)
à p processeurs ne peut pas être plus de
O(log(p)) fois plus rapide que le meilleur algorithme PRAM EREW à p processeurs pour le
même problème.
.3cm
Soit en effet un un algorithme CRCW à p processeurs. On va simuler chaque pas de cet
algorithme en O(log(p)) pas
d'un algorithme EREW. On va pour ce faire utiliser un tableau auxiliaire A de p éléments, qui
va nous permettre de réorganiser les accès mémoire. Quand un processeur Pi de l'algorithme
CRCW écrit une donnée xi à l'adresse li en mémoire, le processeur Pi de
l'algorithme EREW effectue l'écriture exclusive A[i]=(li,xi). On trie alors le
tableau A suivant la première coordonnée en temps O(log(p)) (voir algorithme de Cole,
[RL03]). Une fois A trié, chaque processeur Pi de l'algorithme EREW inspecte les deux
cases adjacentes A[i]=(lj,xj) et A[i-1]=(lk,xk), où 0 £ j, k £ p-1. Si
lj ¹ lk ou si i=0, le processeur Pi écrit la valeur xj à l'adresse lj, sinon
il ne fait rien. Comme A est trié suivant la première coordonnée, l'écriture est bien
exclusive.
On a représenté ce codage, à travers les opérations effectuées sur le tableau A, à
la figure 4.3.
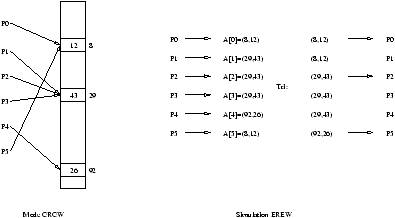
Figure 4.3: Codage d'un algorithme CRCW sur une PRAM EREW
Voici maintenant un autre théorème de simulation, qui a des applications plus surprenantes
que l'on pourrait croire au premier abord:
Théorème (Brent)
Soit A un algorithme comportant un nombre total de m opérations et qui s'exécute en temps t sur
une PRAM (avec un nombre de processeurs quelconque). Alors on peut simuler A en temps O(m/p+t
) sur une PRAM de même type avec p processeurs.
.3cm
En effet, à l'étape i, A effectue m(i) opérations, avec åi=1n m(i)=m. On
simule l'étape i avec p processeurs en temps é m(i)/p ù £ m(i)/p+1.
On obtient le résultat en sommant sur les étapes.
.2cm
Reprenons l'exemple du calcul du maximum, sur une PRAM EREW. On peut agencer ce calcul en temps
O(log n) à l'aide d'un arbre binaire. A l'étape un, on procède paire par paire avec é
n/2 ù processeurs, puis on continue avec les maxima des paires deux par deux etc. C'est
à la première étape qu'on a besoin du plus grand nombre de processeurs, donc il en faut
O(n). Formellement, si n=2m, si le
tableau A est de taille 2n, et si on veut calculer le maximum des n éléments de A en
position A[n], A[n+1],...,A[2n-1], on obtient le résultat dans A[1] après
exécution de l'algorithme:
for (k=m-1; k>=0; k--)
for each j from 2^k to 2^(k+1)-1 in parallel
A[j] = max(A[2j],A[2j+1]);
Supposons que l'on dispose maintenant de p < n processeurs. Le théorème de Brent nous dit
que l'on peut simuler l'algorithme précédent en temps O(n/p+log n),
car le nombre d'opérations total est m=n-1. Si on choisit p=n/log n, on obtient
la même complexité, mais avec moins de processeurs!
.2cm
Tout ceci nous donne à penser qu'il existe sans doute une bonne notion de comparaison des
algorithmes, sur des machines PRAM éventuellement différentes.
Soit P un problème de taille n à résoudre, et soit Tseq(n) le temps du meilleur
algorithme séquentiel connu pour résoudre P. Soit maintenant un algorithme parallèle
PRAM qui résout P en temps Tpar(p) avec p processeurs. Le facteur d'accélération
est défini comme:
et l'efficacité comme
Enfin, le travail de l'algorithme est Wp=pTpar(p)
Le résultat suivant montre que l'on peut conserver le travail par simulation:
Proposition
Soit A un algorithme qui s'exécute en temps t sur une PRAM avec p processeurs. Alors
on peut simuler A sur une PRAM de même type avec p' £ p processeurs, en temps
O(tp/p').
.3cm
En effet, avec p' processeurs, on simule chaque étape de A en temps proportionnel à
é p/p' ù. On obtient donc un temps total de
O(p/p't)=O(tp/p').
4.5 Tris et réseaux de tris
On a vu l'importance de l'existence d'un algorithme de tri en O(log n) pour les théorèmes
de la section précédente. On va se contenter ici de présenter un algorithme de
tri très simple, dit réseau de tri pair-impair, ceci dans un double but. Le premier est de montrer
que l'on peut paralléliser efficacement un algorithme de tri, et que l'on peut en déduire
des implémentations effectives. Le deuxième est de montrer
une classe particulière de machines PRAM, spécialement introduites pour ces types de problèmes,
qui sont les réseaux de tri.
Un réseau de tri est en fait une machine constituée uniquement d'une brique très simple, le
comparateur (voir figure 4.4). Le comparateur est un ``circuit'' qui prend
deux entrées, ici, a et b, et qui renvoie deux sorties: la sortie ``haute'' est min(a,b),
la sortie ``basse'' est max(a,b).
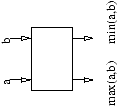
Figure 4.4: Un comparateur.
Donnons maintenant l'exemple du réseau de tri pair-impair.
Ce réseau est formé d'une succession de lignes de comparateurs. Si on désire trier n=2p
éléments, on positionne p copies du réseau formé de deux lignes, dont la première
consiste en p comparateurs prenant en entrées les p paires de fils 2i-1 et 2i, 1 £ i £ p
(étape impaire), et dont la seconde consiste en p-1 comparateurs prenant en entrées les p-1 paires
de fils 2i et 2i+1, 1 £ i £ p-1 (étape paire); voir la figure 4.5 pour
n=8. Bien sûr, il faut bien n=2p telles lignes, car si on suppose que l'entrée est ordonnée
dans le sens décroissant, de gauche à droite, il va falloir faire passer la valeur gauche (en haut)
à droite (en bas), ainsi que la valeur droite (en haut) à gauche (en bas).
Il y a un total de p(2p-1)=n(n-1)/2 comparateurs dans le réseau. Le
tri s'effectue en temps n, et le travail est de O(n3). C'est donc sous-optimal. Certes, moralement,
le travail est réellement de O(n2) (ce qui reste sous-optimal) car à tout moment, il n'y a que de l'ordre de n processeurs
qui sont actifs. C'est l'idée de l'algorithme que nous écrivons maintenant, mais que l'on ne peut
pas écrire dans les réseaux de tris, dans lequel on réutilise
les mêmes processeurs pour les différentes étapes du tri pair-impair.
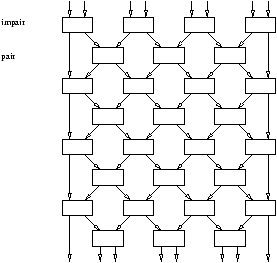
Figure 4.5: Réseau de tri pair-impair pour n=8.
Prenons néanmoins un peu d'avance sur les chapitres concernant la distribution, en indiquant
comment ces idées qui pourraient paraître bien peu réalistes, trouvent des applications
bien naturelles. Supposons que nous ayons un réseau linéaire de processeurs
dans lequel les processeurs ne peuvent communiquer qu'avec leurs voisins de
gauche et de droite (sauf pour les deux extrémités, mais cela a peu d'importance ici, et
on aurait pu tout à fait considérer un réseau en anneau comme on en verra à la section
8.3).
Supposons que l'on ait n données à trier et que l'on dispose de p processeurs, de telle
façon que n est divisible par p. On va mettre les données à trier par paquet de n/p
sur chaque processeur. Chacune de ces suites est triée en temps O(n/plog n/p). Ensuite
l'algorithme de tri fonctionne en p étapes d'échanges alternés, selon le principe du
réseau de tri pair-impair, mais en échangeant des suites de taille n/p à la place
d'un seul élément. Quand deux processeurs voisins communiquent, leurs deux suites de taille n/p
sont fusionnées, le processeur de gauche conserve la première moitié, et celui de droite, la
deuxième moitié. On obtient donc un temps de calcul en O(n/plog n/p +n) et un
travail de O(n(p+log n/p)). L'algorithme est optimal pour p £ log n.
Chapter 5 Coordination de processus
Dans ce chapitre, nous reprenons la programmation des threads JAVA, en y introduisant les mécanismes
d'exclusion mutuelle indispensables, comme nous allons le voir maintenant, pour assurer la correction
de bon nombre de programmes parallèles échangeant des données par mémoire partagée.
5.1 Problème
Modifions la classe Compte du chapitre 3, afin de pouvoir faire des
opérations dessus, voir figure 5.1.
public class Compte {
private int valeur;
Compte(int val) {
valeur = val;
}
public int solde() {
return valeur;
}
public void depot(int somme) {
if (somme > 0)
valeur+=somme;
}
public boolean retirer(int somme) throws InterruptedException {
if (somme > 0)
if (somme <= valeur) {
Thread.currentThread().sleep(50);
valeur -= somme;
Thread.currentThread().sleep(50);
return true;
}
return false;
}
}
|
Figure 5.1: Opérations simples sur un compte bancaire.
On fournit ainsi une méthode solde qui renvoie la somme qui reste sur son compte,
une méthode depot qui permet de créditer son compte d'une somme positive, et enfin,
une méthode retirer qui permet, si son compte est suffisament créditeur, de retirer une
somme (en liquide par exemple).
On implémente alors une version idéalisée d'un automate bancaire (qui ne gérerait qu'un seul
compte!), voir figure 5.2.
public class Banque implements Runnable {
Compte nom;
Banque(Compte n) {
nom = n; }
public void Liquide (int montant)
throws InterruptedException {
if (nom.retirer(montant)) {
Thread.currentThread().sleep(50);
Donne(montant);
Thread.currentThread().sleep(50); }
ImprimeRecu();
Thread.currentThread().sleep(50); }
public void Donne(int montant) {
System.out.println(Thread.currentThread().
getName()+": Voici vos " + montant + " euros."); }
public void ImprimeRecu() {
if (nom.solde() > 0)
System.out.println(Thread.currentThread().
getName()+": Il vous reste " + nom.solde() + " euros.");
else
System.out.println(Thread.currentThread().
getName()+": Vous etes fauches!");
}
public void run() {
try {
for (int i=1;i<10;i++) {
Liquide(100*i);
Thread.currentThread().sleep(100+10*i);
}
} catch (InterruptedException e) {
return;
}
}
public static void main(String[] args) {
Compte Commun = new Compte(1000);
Runnable Mari = new Banque(Commun);
Runnable Femme = new Banque(Commun);
Thread tMari = new Thread(Mari);
Thread tFemme = new Thread(Femme);
tMari.setName("Conseiller Mari");
tFemme.setName("Conseiller Femme");
tMari.start();
tFemme.start();
}
}
|
Figure 5.2: Un automate bancaire.
On a programmé en dur dans la méthode run() de l'automate bancaire
la transaction suivante: on demande à retirer 100 euros, puis 200, puis 300 et ainsi de suite,
jusqu'à épuisement de ses fonds.
Une exécution typique est la suivante:
% java Banque
Conseiller Mari: Voici vos 100 euros.
Conseiller Femme: Voici vos 100 euros.
Conseiller Mari: Il vous reste 800 euros.
Conseiller Femme: Il vous reste 800 euros.
Conseiller Mari: Voici vos 200 euros.
Conseiller Femme: Voici vos 200 euros.
Conseiller Femme: Il vous reste 400 euros.
Conseiller Mari: Il vous reste 400 euros.
Conseiller Mari: Voici vos 300 euros.
Conseiller Femme: Voici vos 300 euros.
Conseiller Femme: Vous etes fauches!
Conseiller Mari: Vous etes fauches! ...
Conclusion:
le mari a retiré 600 euros du compte commun,
la femme a retiré 600 euros du compte commun,
qui ne contenait que 1000 euros au départ. Il est clair que le programme
de gestion de compte n'est pas correct.
L'explication est simple et nous entraîne à faire un peu de sémantique.
L'exécution de plusieurs threads se fait en exécutant une action insécable
(``atomique'') de l'un des threads, puis d'un autre ou éventuellement du même
etc.
Tous les ``mélanges'' possibles sont permis.
C'est ce que l'on appelle la sémantique par entrelacements; on en représente une portion ci-dessous:
Donnons une idée de la façon de donner une sémantique à un fragment
du langage JAVA (et en supposant les lectures et écritures atomiques).
Nous allons prendre comme langage un langage simple qui comprend comme constructions
(étant donné une syntaxe pour les CONSTANTEs entières et un
ensemble fini de VARIABLEs également entières):
| EXPR |
::= |
CONSTANTE |
| |
VARIABLE |
| |
| |
EXPR+EXPR |
| |
EXPR*EXPR |
| |
| |
EXPR/EXPR |
| |
EXPR-EXPR |
| TEST |
::= |
EXPR==EXPR |
| |
EXPR < EXPR |
| |
| |
EXPR > EXPR |
| |
TEST && TEST |
| |
| |
TEST | | TEST |
| |
! TEST |
| INSTR |
::= |
VARIABLE=EXPR |
| BLOCK |
::= |
e |
| |
INSTR;BLOCK |
| |
| |
if TEST |
| |
|
then BLOCK |
| |
|
else BLOCK ;BLOCK |
| |
| |
while TEST |
| |
|
BLOCK ; |
| |
|
BLOCK |
Appelons L le langage engendré par la grammaire plus haut.
On définit la sémantique d'un BLOCK inductivement sur la syntaxe,
en lui associant ce que l'on appelle un système de transitions. Un
système de transitions est un quadruplet (S,i,E,Tran) où,
-
S est un ensemble d'états,
- i Î S est l'``état initial'',
- E est un ensemble d'étiquettes,
- Tran Í S × E × S est l'ensemble des transitions.
On représente plus communément une transition (s,t,s') Î Tran par le graphe:
s ®t s'
En fait, on représente généralement un système de transitions
comme un graphe orienté et étiqueté, comme le suggère la représentation
graphique de la relation de transition Tran, que nous avons déjà vue.
Donnons maintenant les règles de formation du système de transition
correspondant à un BLOCK. Tout d'abord, appelons environnement une
fonction de VARIABLE vers l'ensemble des entiers relatifs. Un état
du système de transition que nous allons construire sera une paire (l,r)
où l Î L et r est un environnement. Intuitivement, l est le programme
qu'il reste à exécuter et r est l'état courant de la machine, c'est
à dire la valeur courante de toutes ses variables. On a alors:
-
(x=expr;block,r) ®x=expr (block,r[x® [ [ expr ] ](r)])
où [ [ expr ] ] (r) dénote la valeur entière
résultat de l'évaluation de l'expression expr dans l'environnement r
(on ne donne pas les règles formelles évidentes qui donnent un sens précis
à cela).
(if t then b1 else
b2; b3,r) ®then (b1; b3,r)
si [ [ t ] ] (r) = vrai
sinon
(if t then b1 else
b2; b3,r) ®else (b2; b3,r)
(while t b1; b2,r) ®while
(b1;while t b1; b2,r)
si [ [ t ] ] (r) = vrai
sinon
(while t b1; b2,r) ®while
(b2,r)
Maintenant, supposons que l'on ait un ensemble de processus P1,...,Pn
qui chacun sont écrits dans le langage L. On peut encore donner une
sémantique opérationnelle (en termes de systèmes de transitions)
dite par ``entrelacements'' en posant:
-
A chaque Pj on associe par [ [ . ] ] défini plus haut un
système de transition (Sj,ij,Ej,Tranj),
- On définit (S,i,E,Tran)=[ [ P1 | ... | Pn ] ] par:
-
S=S1 × ... × Sn,
- i=(i1,...,in),
- E=E1 È ... È En,
| Tran= |
{ |
(s1,...,sj,...,sn) ®tj
(s1,...,sj',...,sn) où
sj ®tj sj' Î Tranj |
} |
Ce n'est pas tout: jusqu'à présent cela ne donne la sémantique qu'à une
machine parallèle où chacun des processus ne calcule que dans sa mémoire locale. On n'a en effet pas
encore modélisé l'échange d'information entre les processus. Pour ce faire, il faut décider des variables
partagées. Notons VP l'ensemble des variables partagées (les autres étant
locales aux différents processus). Alors il faut changer la sémantique précédente
pour que:
-
S=S1 × ... × Sn × Sg, avec Sg=VP ® ZZ
- la sémantique de l'affectation d'une variable globale modifie Sg et non le
Si particulier du processus en question.
Les exécutions ou traces ou entrelacements dans cette sémantique sont des suites
finies:
s0=i ®t1 s1 ®t2 s2 ... ®tn sn
telles que si-1 ®ti si Î Tran
pour tout i entre 1 et n.
On voit dans un des entrelacements que si les 2 threads tMari et tFemme sont exécutés de telle
façon que
dans retirer, chaque étape est faite en même temps, alors
le test pourra être satisfait par les deux threads en même temps,
qui donc retireront en même temps de l'argent.
Raisonner directement sur la sémantique par entrelacement est en général impossible. On en verra un peu
plus loin une abstraction (au sens de [CC77]) un peu plus gérable, les schémas de preuve à la Hoare.
Le domaine de la sémantique, de la preuve et de l'analyse statique de programmes (parallèles et distribués)
sortent du cadre de ce cours, on pourra se reporter aux cours du MPRI pour en savoir plus.
5.2 Une solution: synchronized
Une solution est de
rendre ``atomique'' le fait de retirer de l'argent. Cela veut dire que la méthode
retirer sera considérée comme une action élémentaire, non-interruptible par une autre
instance de retirer. Dis autrement
encore, retirer s'exécutera de façon exclusive: une seule instance de cette méthode pourra
être exécutée à tout instant.
Cela se fait en JAVA en déclarant ``synchronisée'' la méthode retirer
de la classe Compte:
public synchronized boolean retirer(int somme)
Maintenant l'exécution typique paraît meilleure:
% java Banque
Conseiller Mari: Voici vos 100 euros.
Conseiller Femme: Voici vos 100 euros.
Conseiller Mari: Il vous reste 800 euros.
Conseiller Femme: Il vous reste 800 euros.
Conseiller Mari: Voici vos 200 euros.
Conseiller Mari: Il vous reste 400 euros.
Conseiller Femme: Voici vos 200 euros.
Conseiller Femme: Il vous reste 400 euros.
Conseiller Mari: Voici vos 300 euros.
Conseiller Femme: Il vous reste 100 euros.
Conseiller Mari: Il vous reste 100 euros.
Conseiller Femme: Il vous reste 100 euros.
Conseiller Mari: Il vous reste 100 euros...
Le résultat est maintenant que
le mari a tiré 600 euros,
la femme a tiré 300 euros,
et il reste bien 100 euros dans le compte commun, ouf!
Remarquez que synchronized peut aussi s'utiliser sur un morceau de
code: étant donné
un objet obj:
synchronized(obj) {
BLOCK }
permet d'exécuter BLOCK en exclusion mutuelle.
5.3 Moniteurs
Chaque objet fournit un verrou, mais aussi un mécanisme de mise en attente
(forme primitive de communication inter-threads; similaire aux variables de conditions
ou aux moniteurs [Hoa74]).
void wait() attend l'arrivée d'une condition sur l'objet sur lequel
il s'applique (en général this). Il doit être
appelé depuis l'intérieur d'une méthode ou d'un bloc synchronized
(il y a aussi une version avec timeout).
void notify() notifie un thread en attente d'une condition, de
l'arrivée de celle-ci. De même, cette méthode doit être appelée depuis
une méthode déclarée synchronized.
Enfin, void notify_all() fait la
même chose mais pour tous les threads en attente
sur l'objet.
5.4 Sémaphores
5.4.1 Sémaphores binaires
Un sémaphore binaire est un objet sur lequel on peut appliquer les méthodes
P(): un processus ``acquiert'' ou ``verrouille'' le sémaphore, et
V(): un processus ``relâche'' ou ``déverrouille'' le sémaphore. Tant
qu'un processus a un verrou sur le sémaphore, aucun autre ne peut l'obtenir.
public class Semaphore {
int n;
String name;
public Semaphore(int max, String S) {
n = max;
name = S;
}
public synchronized void P() {
if (n == 0) {
try {
wait();
} catch(InterruptedException ex) {};
}
n--;
System.out.println("P("+name+")");
}
public synchronized void V() {
n++;
System.out.println("V("+name+")");
notify();
}
}
|
Figure 5.3: Implémentation de sémaphores.
Cela permet de réaliser l'exclusion mutuelle, donc l'accès par
des processus à des sections critiques, comme on le montre à la
figure 5.4.
public class essaiPV extends Thread {
static int x = 3;
Semaphore u;
public essaiPV(Semaphore s) {
u = s;
}
public void run() {
int y;
// u.P();
try {
Thread.currentThread().sleep(100);
y = x;
Thread.currentThread().sleep(100);
y = y+1;
Thread.currentThread().sleep(100);
x = y;
Thread.currentThread().sleep(100);
} catch (InterruptedException e) {};
System.out.println(Thread.currentThread().
getName()+": x="+x);
// u.V();
}
public static void main(String[] args) {
Semaphore X = new Semaphore(1,"X");
new essaiPV(X).start();
new essaiPV(X).start();
}
}
|
Figure 5.4:
Une exécution typique de ce programme (où on a commenté les lignes u.P()
et u.V()) est la suivante:
% java essaiPV
Thread-2: x=4
Thread-3: x=4
En effet, dans ce cas, les deux processus s'exécutent de façon à peu près synchrone,
lisent tous les deux x et trouvent la valeur 3, incrémentent en même temps leur copie locale,
pour écrire la valeur 4 dans x.
Maintenant, si on décommente u.P() et u.V(), on a par exemple:
% java essaiPV
P(X)
Thread-2: x=4
V(X)
P(X)
Thread-3: x=5
V(X)
La seule autre exécution possible est celle dans laquelle c'est le Thread-3 qui aurait
calculé 4 et le Thread-2 qui aurait calculé 5. Dans ce cas (c'est un exemple de programme
séquentialisable, voir section 5.6), l'exclusion mutuelle assurée par le sémaphore binaire
u permet de faire en sorte que les exécutions parallèles sont toutes ``équivalentes'' à une des exécutions
séquentielles, dans n'importe quel ordre, de l'ensemble des processus présents, considérés comme
insécables.
5.4.2 Un peu de sémantique
On va rajouter à notre langage L les primitives P(.) et
V(.).
La sémantique par systèmes de transitions change assez peu:
-
On rajoute dans l'ensemble d'états S du système de transitions
une composante nouvelle qui est une fonction k: VARIABLE ®
{0,1}. Donc S=(S1,...,Sn,Sg,k). Cette fonction k représente
le fait qu'une variable est verrouillée par un processus ou non,
- i=(P1,...,Pn,k0) où k0 est la fonction qui donne
uniformément 1 (aucune variable n'est encore verrouillée),
- E contient maintenant les nouvelles actions Px et Vx pour toutes
les variables x du programme,
- On a de nouvelles transitions dans Tran de la forme:
(b1,...,Px;bj,...,bn,k) ®Px (b1,...,bj,...,bn,k')
si k(x)=1; et alors k'(y)=k(y) pour tout y ¹ x et
k'(x)=0, et,
(b1,...,Vx;bj,...,bn,k) ®Vx (b1,...,bj,...,bn,k')
avec k'(y)=k(y) pour tout y ¹ x et
k'(x)=1.
Ceci implique, par omission en quelque sorte, qu'aucune exécution d'un Px n'est possible si k(x)=0,
c'est à dire quand la ressource x n'est pas disponible. C'est ce qui permet de modéliser le blocage d'un
processus en attendant la libération d'une ressource, et donc l'exclusion mutuelle.
L'apparition de ces nouvelles transitions contraint en fait les entrelacements
possibles. Si on ``abstrait'' ce système de transition (et le langage de base)
à de simples suites de verrouillages et déverrouillages de variables partagées,
on peut facilement se rendre compte de ce qui peut se passer.
Un des problèmes les plus courants est d'avoir voulu trop protéger
les accès partagés et d'aboutir à une situation où les
processus se bloquent mutuellement; on dit alors qu'il y a une étreinte fatale,
ou encore que le système de transition a des points morts (des états
desquels aucune transition n'est possible, mais qui ne sont pas des états finaux
autorisés: ces états finaux autorisés seraient uniquement
en général des n-uplets des états finaux de chacun des processus).
Un exemple classique est donné par le programme ``abstrait'' suivant constitué
des deux processus:
A=Pa;Pb;Va;Vb
B=Pb;Va;Vb;Va
En regardant la sémantique par entrelacements, on trouve assez vite qu'une
exécution synchrone de A et de B rencontre un point mort: en
effet dans ce cas A (respectivement B) acquiert a (respectivement
b) et attend ensuite la ressource b (respectivement a).
Une image pratique (qui s'abstrait élégamment de la lourdeur
de la représentation des entrelacements) est d'utiliser une image géométrique
continue, les ``progress graphs'' (E.W.Dijkstra (1968)), en français, ``graphes
d'avancement''.
Associons en effet à chaque processus une coordonnée dans un espace IRn
(n étant le nombre de processus).
Chaque coordonnée xi représente en quelque sorte le temps local du
ième processus. Les états du système parallèle sont donc des
points dans cet espace IRn (inclus dans un hyper-rectangle dont les bornes
en chaque coordonnée sont les bornes des temps locaux d'exécution de
chaque processus). Les traces d'exécution sont
les chemins continus et croissants dans chaque coordonnée. Dans la figure
suivante, on a représenté le graphe de processus correspondant à nos
deux processus A et B.
On constate que certains points dans le carré unité ne sont pas des états
valides du programme parallèle. Prenons un point qui a pour coordonnée
T1 un temps local compris entre Pb et Vb et pour coordonnée
T2 un temps local compris également entre Pb et Vb (mais cette fois
pour le processus B). Il ne peut être valide car dans cet état,
les deux processus auraient chacun un verrou sur le même objet b. Cela
contredit la sémantique par système de transitions vue auparavant, c'est
à dire que cela contredit la propriété d'exclusion mutuelle sur b.
On doit également interdire le rectangle horizontal, à cause de la propriété
d'exclusion mutuelle sur la variable partagée a.
On s'aperçoit maintenant que tout chemin d'exécution (partant donc du
point initial en bas à gauche du graphe d'avancement) et qui rentrerait dans
le carré marqué ``dangereux'' doit nécessairement (par sa propriété
de croissance en chaque coordonnée et par sa continuité) aboutir au point
mort, minimum des intersections des deux rectangles interdits. Cette concavité
inférieure est responsable de l'étreinte fatale entre les processus
A et B. De même on s'aperçoit que certains états, dans la
concavité supérieure de la région interdite, sont des états inatteignables
depuis l'état initial. On reviendra la-dessus et sur des critères plus
simples pour trouver si un système a des points morts à la section 5.4.4.
Sachez simplement que ces idées apparemment simples peuvent être développées
extrêmement loin (voir par exemple [Gou03]).
Remarquez également que
synchronized de JAVA
ne fait jamais que P du verrou associé à une méthode
ou à un bloc de code, puis V de ce même verrou à la fin de ce même
code.
Une méthode M de la classe A qui est synchronized est
équivalente à P(A), corps de M, V(A).
Il y a malgré tout une subtile différence. La construction synchronized
est
purement déclarative et a donc
une portée définie statiquement, contrairement à l'utilisation de P
et V.
On retrouvera des considérations sémantiques plus simples, dans le cas du passage
de messages, et des approches de preuve de programmes, dans le TD consacré à l'algèbre
de processus CCS.
5.4.3 Un complément sur la JVM
Pour bien comprendre la sémantique des communications inter-threads en JAVA,
il nous faut expliquer un peu en détail comment la JVM traite les accès
mémoire des threads.
Toutes les variables (avec leurs verrous correspondants et la liste des
threads en attente d'accès)
de tous les threads sont stockées dans la mémoire
gérée par la JVM correspondante. Bien évidemment, les variables locales
d'un thread ne peuvent pas être accédées par d'autres threads, donc on
peut imaginer que chaque thread a une mémoire locale et a accès à une
mémoire globale.
Pour des raisons d'efficacité, chaque thread a une copie locale des variables
qu'il doit utiliser, et il faut bien sûr que des mises à jour de la mémoire
principale (celle gérée par la JVM) soient effectuées, de façon cohérente.
Plusieurs actions atomiques (c'est à dire non interruptibles, ou encore
qui ne s'exécuteront qu'une à la fois sur une JVM)
peuvent être effectuées pour gérer ces copies locales
de la mémoire principale, au moins pour les types simples (int, float...).
Ces actions décomposent les accès mémoires qui sont nécessaires à l'interprétation d'une affectation JAVA:
-
les actions qu'un thread peut exécuter sont:
-
use transfère le contenu de la copie locale d'une variable à
la machine exécutant le thread.
- assign transfère une valeur de la machine exécutant le thread
à la copie locale d'une variable de ce même thread.
- load affecte une valeur venant de la mémoire principale (après
un read, voir plus loin) à la copie locale à un thread d'une variable.
- store transfère le contenu de la copie locale à un thread d'une
variable à la mémoire principale (qui va ainsi pouvoir faire un write,
voir plus loin).
- lock réclame un verrou associé à une variable à la mémoire
principale.
- unlock libère un verrou associé à une variable.
- les actions que la mémoire principale (la JVM) peut exécuter sont:
-
read transfère le contenu d'une variable de la mémoire principale
vers la mémoire locale d'un thread (qui pourra ensuite faire un load).
- write affecte une valeur transmise par la mémoire locale d'un
thread (par store) d'une variable dans la mémoire principale.
Pour les types ``plus longs'' comme double et long, la spécification
permet tout à fait que load, store, read et write
soient non-atomiques. Elles peuvent par exemple être composées de deux
load atomiques de deux ``sous-variables'' int de 32 bits.
Le programmeur doit donc faire attention à synchroniser ses accès à
de tels types, s'ils sont partagés par plusieurs threads.
L'utilisation par la JVM de ces instructions élémentaires est soumise à
un certain nombre de contraintes, qui permettent de définir la sémantique fine
des accès aux ressources partagées de JAVA. Tout d'abord, pour un thread
donné, à tout lock correspond plus tard une opération unlock.
Ensuite, chaque opération load est associée à une opération read qui la précède; de même chaque store est associé à une
opération write qui la suit.
Pour une variable donnée et un thread donné, l'ordre dans lequel des read
sont faits par la mémoire locale (respectivement les write) est le même
que l'ordre dans lequel le thread fait les load (respectivement les
store). Attention, ceci n'est vrai que pour une variable donnée!
Pour les variables volatile, les règles sont plus contraignantes car
l'ordre est aussi respecté entre les read/load et les write/store
entre les variables. Pour les volatile on impose également que les
use suivent immédiatement les load et que les store suivent
immédiatement les assign.
Pour bien comprendre tout cela prenons deux exemples classiques, aux figures
5.6 et 5.7 respectivement. On utilise ces classes dans deux threads
de la même façon, on en donne donc le code à la figure
5.5 uniquement dans le cas de Exemple1.
class Essai1 extends Thread {
public Essai1(Exemple1 e) {
E = e;
}
public void run() {
E.F1();
}
private Exemple1 E;
}
class Essai2 extends Thread {
public Essai2(Exemple1 e) {
E = e;
}
public void run() {
E.G1();
}
private Exemple1 E;
}
class Lance {
public static void main(String args[]) {
Exemple1 e = new Exemple1();
Essai1 T1 = new Essai1(e);
Essai2 T2 = new Essai2(e);
T1.start();
T2.start();
System.out.println("From Lance a="+e.a+" b="+e.b);
}
}
|
Figure 5.5: Classe Essai1.
class Exemple1 {
int a = 1;
int b = 2;
void F1() {
a = b;
}
void G1() {
b = a;
}
}
|
Figure 5.6: Classe Exemple1.
class Exemple2 {
int a = 1;
int b = 2;
synchronized void F2() {
a = b;
}
synchronized void G2() {
b = a;
}
}
|
Figure 5.7: Classe Exemple2
Une exécution typique est:
> java Lance
a=2 b=2
Mais il se peut que l'on trouve également:
> java Lance
a=1 b=1
ou encore
> java Lance
a=2 b=1
En fait, pour être plus précis, les contraintes d'ordonnancement font
que les chemins possibles d'exécution sont les entrelacements des 2 traces
séquentielles
read b ® load b ® use b ® assign a ®
store a ® write a
pour le thread Essai1 et
read a ® load a ® use a ® assign b ®
store b ® write b
pour le thread Essai2. Appelons la1, lb1 (respectivement la2 et lb2) les copies locales des variables
a et b pour le thread Essai1 (respectivement pour le thread Essai2).
Alors on peut avoir les entrelacement suivants (modulo les commutations des
read a et read b, ce qui n'a aucune influence sur le calcul):
read b ® write a ® read a ® write b
read a ® write b ® read b ® write a
read a ® read b ® write b ® write a
Dans le premier cas l'état de la machine est la1=2, lb1=2, a=2, b=2,
la2=2 et lb2=2. Dans le deuxième on a la1=1, lb1=1, a=1, b=1,
la2=1 et lb2=1. Enfin dans le troisième, on a la1=2, lb1=2, a=2, b=1,
la2=1 et lb2=1.
Si on utilise la version synchronisée de Exemple1, qui est Exemple2
à la figure 5.7, alors on n'a plus que les deux premiers
ordonnancements qui soient possibles:
read b ® write a ® read a ® write b
read a ® write b ® read b ® write a
5.4.4 Quelques grands classiques
Exerçons un peu nos talents sur des problèmes classiques du parallélisme
(que vous aurez peut-être vu par ailleurs, par exemple en cours de système
d'exploitation).
Le premier problème est celui des
philosophes qui dînent (introduit par E. W. Dijkstra [Dij68]).
Dans le cas général, on a n philosophes assis autour d'une table (plus ou moins) ronde:
avec chacun une fourchette à sa gauche et une autre à sa droite. On n'a pas
représenté ici le sujet principal: le bol de spaghettis supposé être au
centre. Les philosophes voulant manger, doivent utiliser les 2 fourchettes en même
temps pour se servir de spaghettis. Un des premiers ``protocoles'' venant à l'esprit
est celui dans lequel chaque philosophe essaie d'attraper sa fourchette gauche,
puis droite, se sert et enfin repose la fourchette gauche puis droite. Cela donne
en JAVA le code de la figure 5.8.
public class Phil extends Thread {
Semaphore LeftFork;
Semaphore RightFork;
public Phil(Semaphore l, Semaphore r) {
LeftFork = l;
RightFork = r;
}
public void run() {
try {
Thread.currentThread().sleep(100);
LeftFork.P();
Thread.currentThread().sleep(100);
RightFork.P();
Thread.currentThread().sleep(100);
LeftFork.V();
Thread.currentThread().sleep(100);
RightFork.V();
Thread.currentThread().sleep(100);
} catch (InterruptedException e) {};
}
}
public class Dining {
public static void main(String[] args) {
Semaphore a = new Semaphore(1,"a");
Semaphore b = new Semaphore(1,"b");
Semaphore c = new Semaphore(1,"c");
Phil Phil1 = new Phil(a,b);
Phil Phil2 = new Phil(b,c);
Phil Phil3 = new Phil(c,a);
Phil1.setName("Kant");
Phil2.setName("Heidegger");
Phil3.setName("Spinoza");
Phil1.start();
Phil2.start();
Phil3.start();
} }
|
Figure 5.8: Implémentation des trois philosophes.
Une exécution typique est:
% java Dining
Kant: P(a)
Heidegger: P(b)
Spinoza: P(c)
^C
On constate un interblocage des processus. Comment aurions nous pu nous en douter?
L'explication est simple:
quand
les trois philosophes prennent en même temps leur fourchette gauche, ils attendent
tous leur fourchette droite... qui se trouve être la fourchette gauche de leur
voisin de droite.
On s'aperçoit que ce point mort est simplement dû à un cycle dans les demandes
et attributions des ressources partagées. Essayons de formaliser un peu cela.
Construisons un graphe orienté (le ``graphe de requêtes'') dont les noeuds sont
les ressources et dont les arcs sont comme suit. On a un arc d'un noeud a
vers un noeud b si il existe un processus qui, ayant acquis un verrou sur a
(sans l'avoir relaché), demande un verrou sur b. On étiquette alors cet
arc par le nom du processus en question. Alors on peut facilement montrer
que si le graphe de requêtes est acyclique alors le système constitué
par les threads considérés ne peut pas rentrer en interblocage.
En abstrayant le programme JAVA pour ne s'intéresser plus qu'aux
suites de verrouillages et déverrouillages, on obtient les
trois processus suivants en parallèle:
A=Pa;Pb;Va;Vb
B=Pb;Pc;Vb;Vc
C=Pc;Pa;Vc;Va
Un exemple en est donné à la figure 5.9, correspondant aux
3 philosophes, et ce graphe est bien cyclique.
On pouvait aussi s'en apercevoir sur le graphe d'avancement: le point mort est
du à l'intersection de 3 (=nombre
de processus) hyperrectangles, ou encore
la concavité ``inférieure'' de la figure 5.11...mais cela nous entraînerait
trop loin.
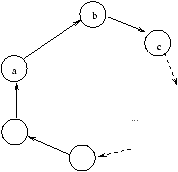
Figure 5.9: Le graphe de requêtes pour n philosophes.
Figure 5.10: Graphe d'avancement des 3 philosophes
Figure 5.11: Point mort des 3 philosophes
La condition sur les graphes de requêtes est
une condition suffisante à l'absence de points morts, et non nécessaire
comme le montre l'exemple suivant (où A, B et C sont
encore 3 threads exécutés en parallèle):
A=Px;Py;Pz;Vx;Pw;Vz;Vy;Vw
B=Pu;Pv;Px;Vu;Pz;Vv;Vx;Vz
C=Py;Pw;Vy;Pu;Vw;Pv;Vu;Vv
dont on trouve le graphe de requêtes (fortement cyclique!) à la
figure 5.12. Pour avoir une idée de pourquoi cette politique d'accès
aux ressources partagées n'a pas de point mort, il faut regarder le graphe
d'avancement, représenté à la figure 5.13. La région
interdite est homéomorphe à un tore (plus ou moins sur l'antidiagonale du cube...
c'est une image bien sûr!) et le chemin passant au milieu du tore n'est jamais
stoppé par une concavité intérieure.
Figure 5.12: Graphe de requêtes pour l'exemple Lipsky/Papadimitriou.
Figure 5.13: Graphe de processus pour le terme de Lipsky et Papadimitriou.
Comment remédier au problème d'interblocage dans le cas des n philosophes?
Il faut réordonnancer
les accès aux variables partagées. Il y a beaucoup de solutions (éventuellement
avec ordonnanceur extérieur). Il y en a en fait une très simple:
on numérote les philosophes, par exemple dans le sens trigonométrique autour
de la table. On impose maintenant que les philosophes
de numéro pair acquièrent la fourchette gauche d'abord, puis la droite et aussi
que
les philosophes de numéro impair acquièrent la fourchette droite d'abord,
puis la gauche. Cela donne (en terme de P et de V):
P1=Pa2;Pa1;Va2;Va1
P2=Pa2;Pa3;Va2;Va3
...
P2k=Pa2k;Pa(2k+1);Va2k;Va(2k+1)
P(2k+1)=Pa(2k+2);Pa(2k+1);Va(2k+2);Va(2k+1)
Le graphe de requêtes est décrit à la figure 5.14, on voit bien
qu'il est acyclique, donc que le système de processus ne rencontre pas de points
morts.
Figure 5.14: Le nouveau graphe de requêtes.
5.4.5 Sémaphores à compteur
On a parfois besoin d'objets qui peuvent être partagés par n processus
en même temps et pas par n+1. C'est une généralisation évidente
des sémaphores binaires (qui sont le cas n=1). Par exemple, on peut avoir
à protéger l'accès à des tampons de messages de capacité n.
On appelle les sémaphores correspondants, les sémaphores à compteur.
Il sont en fait implémentables à partir des sémaphores binaires
[Dij68], comme le fait le code de la figure 5.15.
public class essaiPVsup extends Thread {
static int x = 3;
Semaphore u;
public essaiPVsup(Semaphore s) {
u = s;
}
public void run() {
int y;
u.P();
try {
Thread.currentThread().sleep(100);
y = x;
Thread.currentThread().sleep(100);
y = y+1;
Thread.currentThread().sleep(100);
x = y;
Thread.currentThread().sleep(100);
} catch (InterruptedException e) {};
System.out.println(Thread.currentThread().
getName()+": x="+x);
u.V(); }
public static void main(String[] args) {
Semaphore X = new Semaphore(2,"X");
new essaiPVsup(X).start();
new essaiPVsup(X).start();
}
}
|
Figure 5.15: Utilisation de sémaphores à compteur.
Par exemple:
% java essaiPVsup
Thread-2: P(X)
Thread-3: P(X)
Thread-2: x=4
Thread-2: V(X)
Thread-3: x=4
Thread-3: V(X)
On voit bien que l'on n'a pas d'exclusion mutuelle.
Pour les tampons de capacité bornée cela peut servir comme on l'a déjà dit
(problème du type producteur consommateur) et comme on le montre par un petit
code JAVA à la figure 5.16.
public class essaiPVsup2 extends Thread {
static String[] x = {null,null};
Semaphore u;
public essaiPVsup2(Semaphore s) {
u = s;
}
public void push(String s) {
x[1] = x[0];
x[0] = s;
}
public String pop() {
String s = x[0];
x[0] = x[1];
x[1] = null;
return s; }
public void produce() {
push(Thread.currentThread().getName());
System.out.println(Thread.currentThread().
getName()+": push");
}
public void consume() {
pop();
System.out.println(Thread.currentThread().
getName()+": pop"); }
public void run() {
try {
u.P();
produce();
Thread.currentThread().sleep(100);
consume();
Thread.currentThread().sleep(100);
u.V();
} catch(InterruptedException e) {};
}
public static void main(String[] args) {
Semaphore X = new Semaphore(2,"X");
new essaiPVsup2(X).start();
new essaiPVsup2(X).start();
new essaiPVsup2(X).start();
}
}
|
Figure 5.16: Producteur/consommateur, avec des sémaphores à compteur.
Dans cet exemple, on a 3 processus qui partagent une file à 2 cellules
protégée (en écriture)
par un 2-sémaphore. Chaque processus essaie de produire (push)
et de consommer (pop)
des données dans cette file. Pour que la file ne perde jamais de messages, il faut
qu'elle ne puisse pas être ``partagée'' en écriture par plus de 2 processus en même temps.
Un exemple typique d'exécution est le suivant:
% java essaiPVsup2
Thread-2: P(X)
Thread-2: push
Thread-3: P(X)
Thread-3: push
Thread-2: pop
Thread-3: pop
Thread-2: V(X)
Thread-3: V(X)
Thread-4: P(X)
Thread-4: push
Thread-4: pop
Thread-4: V(X)
5.5 Barrières de synchronisation
Un autre mécanisme de protection, ou plutôt de synchronisation qui est
couramment utilisé dans les applications parallèles est ce qu'on appelle
une barrière de synchronisation. Son principe est que tout processus peut
créer une barrière de synchronisation (commune à un groupe de processus)
qui va permettre de donner un rendez-vous à exactement n processus. Ce
point de rendez-vous est déterminé par l'instruction waitForRest()
dans le code de chacun des processus. On en donne une implémentation
(tirée du livre [OW00]) à la figure 5.17.
L'idée est d'utiliser un compteur du nombre de threads qu'il faut encore attendre
(threads2wa- -it4) et de bloquer tous les processus par un wait tant
que le quorum n'est pas atteint. On débloque alors tout le monde par un
notifyAll. Le champ privé iex est là pour permettre de récupérer
proprement les exceptions.
public class Barrier {
private int threads2Wait4;
private InterruptedException iex;
public Barrier(int nThreads) {
threads2Wait4 = nThreads;
}
public synchronized int waitForRest()
throws InterruptedException {
int threadNum = --threads2Wait4;
if (iex != null) throw iex;
if (threads2Wait4 <= 0) {
notifyAll();
return threadNum;
}
while (threads2Wait4 > 0) {
if (iex != null) throw iex;
try {
wait();
} catch(InterruptedException ex) {
iex = ex;
notifyAll();
}
}
return threadNum;
}
public synchronized void freeAll() {
iex = new InterruptedException("Barrier Released
by freeAll");
notifyAll();
}
}
|
Figure 5.17: Implémentation d'une barrière de synchronisation en JAVA.
Un exemple d'utilisation typique est donné à la figure 5.18.
public class ProcessIt implements Runnable {
String[] is;
Barrier bpStart, bp1, bp2, bpEnd;
public ProcessIt(String[] sources) {
is = sources;
bpStart = new Barrier(sources.length);
bp1 = new Barrier(sources.length);
bp2 = new Barrier(sources.length);
bpEnd = new Barrier(sources.length);
for (int i=0;i<is.length; i++) {
(new Thread(this)).start(); } }
public void run() {
try {
int i = bpStart.waitForRest();
doPhaseOne(is[i]);
bp1.waitForRest();
doPhaseTwo(is[i]);
bp2.waitForRest();
doPhaseThree(is[i]);
bpEnd.waitForRest();
} catch(InterruptedException ex) {};
}
public void doPhaseOne(String ps) {
}
public void doPhaseTwo(String ps) {
}
public void doPhaseThree(String ps) {
}
static public void main(String[] args) {
ProcessIt pi = new ProcessIt(args);
}
}
|
Figure 5.18: Essai des barrières de synchronisation.
5.6 Un exemple d'ordonnancement: séquentialisation
Considérez le problème suivant. On a une base de données distribuée
qui contient les réservations aériennes et hotelières d'une grande compagnie. Les
clients réservent leurs billets au travers d'agences dans le monde entier,
qui donc n'ont aucun moyen direct de se synchroniser. Les informations sur
les réservations sont dans une mémoire d'ordinateur unique quelque part sur
la planète. Supposons que nous ayons deux clients, Bill et Tom, les deux habitant
Paris, et souhaitant prendre chacun deux places sur un avion pour New York.
Supposons
encore que ces deux clients veulent en fait exactement les mêmes vols
et qu'il ne reste plus que
deux places sur ce vol. Comment faire en sorte de servir ces deux clients
de façon cohérente, c'est-à-dire que Bill ou Tom ait les deux places, mais pas
seulement une partie (car sinon, ils ne voudraient pas partir du tout)?
Regardons le programme implémentant les requêtes de Bill et Tom de la
figure 5.19.
public class Ticket {
String nom;}
public class Requete extends Thread {
Ticket Aller;
Ticket Aller2;
Semaphore u;
Semaphore v;
public Requete(Ticket t, Ticket s,
Semaphore x, Semaphore y) {
Aller = t;
Aller2 = s;
u = x;
v = y; }
public void run() {
try {
u.P();
Thread.currentThread().sleep(100);
if (Aller.nom == null)
Aller.nom = Thread.currentThread().
getName();
Thread.currentThread().sleep(100);
u.V();
} catch (InterruptedException e) {};
try {
v.P();
Thread.currentThread().sleep(100);
if (Aller2.nom == null)
Aller2.nom = Thread.currentThread().
getName();
Thread.currentThread().sleep(100);
v.V();
} catch (InterruptedException e) {};
}
}
public class Serial {
public static void main(String[] args) {
Semaphore a = new Semaphore(1,"a");
Semaphore b = new Semaphore(1,"b");
Ticket s = new Ticket();
Ticket t = new Ticket();
Requete Bill = new Requete(s,t,a,b);
Requete Tom = new Requete(t,s,b,a);
Bill.setName("Bill");
Tom.setName("Tom");
Bill.start();
Tom.start();
try {
Tom.join();
Bill.join();
} catch(InterruptedException e) {};
System.out.println("Le premier billet Paris->New York
est au nom de: "+s.nom);
System.out.println("Le deuxieme billet New York->Paris
est au nom de: "+t.nom); } }
|
Figure 5.19: Base de donnée de billets d'avions.
Le résultat est:
% java Serial
Bill: P(a)
Tom: P(b)
Bill: V(a)
Tom: V(b)
Bill: P(b)
Tom: P(a)
Bill: V(b)
Tom: V(a)
Le premier billet Paris->New York est au nom de: Bill
Le deuxieme billet Paris->New York est au nom de: Tom
Ce qui n'est pas très heureux: en fait aucun des deux clients ne sera content
car chacun pourra partir, mais seul! Ceci est du au fait que les demandes ont été
entrelacées.
Il est facile de voir que le chemin d'exécution qui vient d'être pris correspond
à un chemin sur la diagonale du graphe d'avancement (où les deux rectangles du centre représentent
les états interdits):
qui ``mélange'' les transactions de nos deux utilisateurs.
Il existe plusieurs protocoles permettant d'atteindre un état
plus cohérent de la base de données. Par exemple le protocole
``2-phase locking'' (voir [Abi00]) où chacun des deux clients
essaie d'abord de verrouiller tous les billets voulus, avant d'y mettre son
nom et de payer, puis de tout déverrouiller, permet cela. On dit que ce
protocole est ``séquentialisable'', c'est à dire que tous les accès à
la base de données distribuées se font comme si les deux clients étaient
dans une même agence, et surtout dans une file ordonnée...
Quand on change dans Requete, l'ordre des verrous, dans la méthode run(),
on obtient le programme de la figure 5.20 et l'exécution:
public void run() {
try {
u.P();
v.P();
Thread.currentThread().sleep(100);
if (Aller.nom == null)
Aller.nom = Thread.currentThread().
getName();
Thread.currentThread().sleep(100);
Thread.currentThread().sleep(100);
if (Aller2.nom == null)
Aller2.nom = Thread.currentThread().
getName();
Thread.currentThread().sleep(100);
u.V();
v.V();
} catch (InterruptedException e) {};
}
|
Figure 5.20: Une politique d'ordonnancement séquentialisable pour la base de données de billets d'avion.
% java Serial2
Bill: P(a)
Bill: P(b)
Bill: V(a)
Bill: V(b)
Tom: P(b)
Tom: P(a)
Tom: V(b)
Tom: V(a)
Le premier billet Paris->New York est au nom de: Bill
Le deuxieme billet Paris->New York est au nom de: Bill
qui ne satisfait vraiment que Bill mais qui au moins est cohérent!
Evidemment, il est aussi possible dans
ce cas qu'une exécution donne également un interblocage:
% java Serial2
Bill: P(a)
Tom: P(b)
^C
On s'aperçoit que dans le cas de la figure 5.20, le graphe d'avancement
interdit des chemins non séquentialisables, mais effectivement pas les
points morts (les rectangles au centre sont des régions interdites):
Les seules obstructions sont ``au centre'': on peut déformer tout chemin sur l'un des bords, c'est à dire
sur l'ensemble des chemins séquentiels. C'est là
l'essence de la preuve géométrique de correction du protocole 2PL de [Gun94].
Pour enlever le point mort possible, il suffit de réordonnancer la demande de Bill ou de Tom,
pour qu'elle soit dans le même ordre (cf. graphe de requêtes).
Chapter 6 Algorithmes d'exclusion mutuelle (mémoire partagée)
6.1 Peut-on se passer de synchronized?
On cherche à programmer un mécanisme d'``exclusion mutuelle'', en mémoire partagée,
à
partir des primitives que l'on a vues, sauf les primitives
de synchronisation synchronized,
wait et notify. On doit évidemment avoir
une hypothèse de base sur la sémantique du système sous-jacent. On ne
va imposer comme condition que le fait que la lecture et l'écriture en
mémoire sont atomiques, c'est-à-dire que plusieurs lectures et
écritures en parallèle sont en fait exécutées séquentiellement dans
un ordre à priori quelconque. Ceci n'est pas toujours vrai en JAVA, mais nous
présenterons quand même le pseudo-code en JAVA.
On veut donc pouvoir
faire en sorte qu'un thread impose à tous les autres d'être l'unique
à s'exécuter (pendant que les autres attendent leur tour).
En fait, on pourra se déclarer content d'un algorithme d'exclusion mutuelle
seulement s'il satisfait les conditions suivantes:
-
(A) si un thread se trouve en section critique, tout autre thread doit être
en train d'exécuter une section non-critique.
- (B) supposons qu'un groupe de threads I exécute du code dans une
section non-critique, et ne requiert pas encore d'accéder à une section
critique. Supposons maintenant que tous les autres processus (groupe J)
requièrent l'accès à une section critique, mais qu'ils n'en ont pas encore
obtenu la permission. Alors le processus qui doit rentrer en section critique
doit appartenir à J, et cette permission ne doit pas pouvoir être reportée
indéfiniment.
- (C) un thread qui demande à entrer en section critique obtiendra toujours
d'y rentrer au bout d'un temps fini (c'est une propriété d'équité
qui permet d'éviter la famine d'un ou plusieurs processus).
La première
idée qui vienne à l'esprit
est de rajouter aux threads considérés un champ:
public class CS1 extends Thread {
Thread tour = null;
...
}
qui précise quel thread doit s'exécuter. On veut
écrire une méthode:
public void AttendtonTour()
qui attend l'autorisation de s'exécuter, et
public void RendlaMain()
qui autorise les autres threads présents à essayer de s'exécuter.
Pour simuler l'algorithme, on fait en sorte que tous
les threads instances de CS1 aient la même exécution:
public void run() {
while(true) {
AttendtonTour();
System.out.println("C'est le tour de "+
Thread.currentThread().getName());
RendlaMain();
}
}
On en arrive au code naturel de la figure 6.1.
public class CS1 extends Thread {
volatile Thread tour = null;
public void AttendtonTour() {
while (tour != Thread.currentThread()) {
if (tour == null)
tour = Thread.currentThread();
try {
Thread.sleep(100);
} catch (Exception e) {}
}
}
public void RendlaMain() {
if (tour == Thread.currentThread())
tour = null;
}
public void run() {
while(true) {
AttendtonTour();
System.out.println("C'est le tour de "+
Thread.currentThread().getName());
RendlaMain();
} }
public static void main(String[] args) {
Thread Un = new CS1();
Thread Deux = new CS1();
Un.setName("UN");
Deux.setName("DEUX");
Un.start();
Deux.start();
} }
|
Figure 6.1: Une tentative d'algorithme d'exclusion mutuelle.
Mais cela contredit (A) par exemple. Il suffit de considérer
une exécution synchrone des threads et on s'aperçoit que les
deux processus peuvent rentrer dans leur section critique en même temps!
6.2 Premiers algorithmes?
Continuons sur l'idée de la dernière section, et
essayons de programmer une première approximation
de code permettant d'assurer l'exclusion mutuelle. Intéressons-nous
d'abord à un premier cas dans lequel on a seulement
deux processus P0 et P1.
L'idée est
d'assurer que l'on ne puisse jamais être en même temps dans
certaine partie du code (appelée section critique) pour P0 et
P1.
Le premier code auquel on puisse penser
pour Pi (i=0,1) est montré à la figure 6.2.
public class Algorithme1 extends ExclusionMutuelle
{
public Algorithme1() {
turn = 0;
}
public void Pmutex(int t) {
while (turn != t)
Thread.yield();
}
public void Vmutex(int t) {
turn = 1-t;
}
private volatile int turn;
}
|
Figure 6.2: Une autre tentative d'algorithme d'exclusion mutuelle.
Remarquer que l'entier turn est déclaré en volatile c'est-à-dire
qu'il est susceptible d'être modifié à tout moment par l'extérieur
(un autre thread par exemple). Cela empêche javac de le placer
dans un registre en cours d'exécution, pour optimiser le code (ce serait
en l'occurrence une optimisation fausse dans notre cas).
Ce code est une instance de la classe abstraite ExclusionMutuelle de la
figure 6.3.
public abstract class ExclusionMutuelle
{
public static void Critique() {
try {
Thread.sleep((int) (Math.random()*3000));
}
catch (InterruptedException e) { }
}
public static void nonCritique() {
try {
Thread.sleep((int) (Math.random()*3000));
}
catch (InterruptedException e) { }
}
public abstract void Pmutex(int t);
public abstract void Vmutex(int t);
}
|
Figure 6.3: Simulation des sections critiques et non-critiques.
Pour tester cet algorithme, on utilise des tâches très simples, simulant
l'entrée et la sortie d'une section critique, voir figure 6.4.
public class Tache extends Thread
{
public Tache(String n,int i,ExclusionMutuelle s) {
name = n;
id = i;
section = s;
}
public void run() {
while (true) {
section.Pmutex(id);
System.out.println(name+" est en section critique");
ExclusionMutuelle.Critique();
section.Vmutex(id);
System.out.println(name+" est sorti de la section critique");
ExclusionMutuelle.nonCritique();
}
}
private String name;
private int id;
private ExclusionMutuelle section;
}
|
Figure 6.4: Thread appelant les algorithmes d'exclusion mutuelle.
Et enfin on utilise un main qui crée et lance deux tâches, voir figure 6.5.
public class Test
{
public static void main(String args[]) {
ExclusionMutuelle alg = new Algorithme1();
Tache zero = new Tache("Tache 0",0,alg);
Tache un = new Tache("Tache 1",1,alg);
zero.start();
un.start();
}
}
|
Figure 6.5: Lancement de deux tâches en parallèle.
Mais
avec Algorithme1, les processus
ne peuvent entrer en section critique qu'à tour
de rôle, ce qui contredit (B) (mais il est vrai que cet algorithme
satisfait à (A) et (C), si on suppose que chaque section critique se déroule
en temps fini).
En fait, on peut prouver (voir [Lyn96])
que pour résoudre le problème de l'exclusion
mutuelle entre n processus dans notre cadre, il faut au moins n
variables partagées distinctes, donc il est clair qu'il faut un peu
compliquer le code précédent (n=2, mais seulement une variable partagée,
turn!).
Pour résoudre la difficulté précédente, il faut s'arranger pour
connaître l'état de chaque processus afin de
prendre une décision. Un essai de solution serait le code de la figure 6.6.
public class Algorithme2 extends ExclusionMutuelle
{
public Algorithme2() {
flag[0] = false;
flag[1] = false;
}
public void Pmutex(int t) {
int other;
other = 1-t;
flag[t] = INIT;
while (flag[other] == true)
Thread.yield();
}
public void Vmutex(int t) {
flag[t] = false;
}
private volatile boolean[] flag = new boolean[2];
}
|
Figure 6.6: Deuxième tentative d'implémentation d'un algorithme d'exclusion mutuelle.
Si on remplace INIT par false on s'aperçoit que la condition
(A)
d'exclusion mutuelle n'est pas satisfaite!
Pour s'en convaincre il suffit de considérer l'exécution suivante (les deux premières colonnes
représentent l'exécution du processeur 0 et du processeur 1 respectivement, les deux dernières
colonnes donnent les valeurs prises par le tableau flag):
| zero |
un |
flag[0] |
flag[1] |
| flag[1]=false ?: OUI |
flag[0]=false ?: OUI |
false |
false |
| flag[0]:= true |
flag[1]:=true |
true |
true |
| Section Critique |
Section Critique |
- |
- |
Si d'autre part, on fait INIT=true, la même exécution (synchrone)
fait que les deux processus bouclent indéfiniment, contredisant (B) et (C)!
On propose alors le code de la figure 6.7, toujours plus compliqué...
public class Algorithme4 extends ExclusionMutuelle
{
public Algorithme4() {
flag[0] = false;
flag[1] = false;
}
public void Pmutex(int t) {
int other;
other = 1-t;
flag[t] = true;
while (flag[other] == true) {
flag[t] = false;
while (flag[other])
Thread.yield();
flag[t] = true;
}
public void Vmutex(int t) {
flag[t] = false;
}
private volatile boolean[] flag = new boolean[2];
}
|
Figure 6.7: Autre tentative d'algorithme d'exclusion mutuelle.
Il réalise bien l'exclusion mutuelle mais
peut causer un interblocage si les deux processus s'exécutent
de façon purement synchrone. A ce moment là,
après la première affectation, les deux
tests de la boucle while sont vrais, d'où les deux flag sont mis
à false simultanément puis à true et ainsi de suite.
Les programmes de zero et de un bouclent avant la portion
Section Critique.
Tout cela paraît sans issue. En fait,
une solution est d'instaurer une règle de politesse entre les processeurs.
C'est l'algorithme de Dekker (1965), à la figure 6.8.
6.3 Algorithme de Dekker
public class Dekker extends ExclusionMutuelle
{
public Dekker() {
flag[0] = false;
flag[1] = false;
turn = 0;
}
public void Pmutex(int t) {
int other;
other = 1-t;
flag[t] = true;
while (flag[other] == true) {
if (turn == other) {
flag[t] = false;
while (turn == other)
Thread.yield();
flag[t] = true;
}
}
}
public void Vmutex(int t) {
turn = 1-t;
flag[t] = false;
}
private volatile int turn;
private volatile boolean[] flag = new boolean[2];
}
|
Figure 6.8: Algorithme de Dekker.
Il réalise
l'exclusion mutuelle
sans blocage mutuel. L'équité (la condition (C)) est vérifiée
si l'ordonnanceur de tâche est lui-même équitable, ce que l'on
supposera.
Considérons le code plus simple de la figure 6.9, proposé par Hyman en 1966.
public class Hyman extends ExclusionMutuelle
{
public Hyman() {
flag[0] = false;
flag[1] = false;
turn = 0;
}
public void Pmutex(int t) {
int other = 1-t;
flag[t]= true;
while (turn==other) {
while (flag[other])
Thread.yield();
turn = t;
}
}
public void Vmutex(int t) {
flag[t] = false;
}
private volatile int turn;
private volatile boolean[] flag = new boolean[2];
}
|
Figure 6.9: Algorithme faux d'Hyman.
Il est malheureusement faux car,
si turn est à 0 et un positionne
flag[1] à true puis trouve flag[0] à
false,
alors zero met flag[0] à true, trouve
turn
égal à 0 et rentre en section critique.
un affecte alors
1 à turn et rentre également en section
critique!
Une vraie amélioration de l'algorithme de Dekker est
l'algorithme de Peterson proposé en 1981.
6.4 Algorithme de Peterson
Contentons nous d'abord du cas simple où l'on dispose uniquement de
deux tâches zero et un. Le code
des deux tâches est donné à la figure 6.10.
public class Peterson extends ExclusionMutuelle
{
public Peterson() {
flag[0] = false;
flag[1] = false;
turn = 0;
}
public void Pmutex(int t) {
int other;
other = 1-t;
flag[t] = true;
turn = t;
while (flag[other] && (turn == t))
Thread.yield();
}
public void Vmutex(int t) {
flag[t] = false;
}
private volatile int turn;
private volatile boolean[] flag = new boolean[2];
}
|
Figure 6.10: Algorithme de Peterson.
On a bien alors exclusion mutuelle sans interblocage et
avec équité (pas de famine).
Donnons ici quelques idées de preuve de cet algorithme.
On va décorer le code par des ``assertions'' écrites avec
des prédicats logiques du premier ordre, portant sur les valeurs des variables
du programme (et donc également de celles que l'on vient d'introduire),
avec comme prédicats l'égalité avec des constantes (cela nous suffira
ici). Ces assertions seront introduites entre deux instructions consécutives, c'est-à-dire
qu'elles seront associées à chaque point de contrôle de chaque
processus.
On va introduire, de façon intuitive et pas trop formelle, une méthode
de raisonnement et de preuve sur des processus parallèles (disons, en nombre
n) en mémoire partagée
due à l'origine à S. Owicki et D. Gries [OG75].
Les assertions que l'on rajoute doivent être des ``invariants'' décrivant
des relations logiques entre les valeurs des variables, vraies pour toutes les
exécutions possibles (en particulier tous les ordonnancements des actions
atomiques).
Cela veut dire la chose suivante. Soit T le système de transition donnant
la sémantique du programme considéré. On sait qu'un état de T
est un (n+1)-uplet (c1,...,cn,E) où ci (1 £ i £ n) est
un point de contrôle du ième processus et E est un environnement, c'est-à-dire
une fonction qui à chaque variable du programme associe une valeur.
Alors le système d'assertion A qui à chaque point de contrôle
c (de n'importe quel processus i) associe un prédicat P
est admissible si P est vrai pour l'environnement E
quel que soit l'état (c1,...,cn,E) du système
de transition tel que ci=c.
L'idée est que l'on veut pouvoir inférer quand c'est possible, ou tout du
moins vérifier que les assertions que l'on rajoute dans le code de chacun des
processus disent bien des choses vraies sur toutes les exécutions possibles du
code.
Soit I une instruction ou un bloc d'instructions JAVA. On rajoute des
assertions décrivant ce qui se passe avant et après le code I en
écrivant { p } I { q }.
On a les règles suivantes, pour un fragment de JAVA, qui va nous suffire
pour le moment:
-
{ p[x¬ u] } x=u { p }
| { p1 } |
( |
if B then {p2} I1 {q2} else
{p3}I2 {q3} |
) |
{ q1 } |
| p1 Ù B Þ p2 |
| p1 Ù ¬ B Þ p3 |
| {p2} I1 {q2} |
| {p3}I2{q3} |
| q2 Þ q1 |
| q3 Þ q1 |
| {p1} while B |
{ |
{p2} C {q2} |
} |
{q1} |
| p1 Ù B Þ p2 |
| p1 Ù ¬ B Þ q1 |
| {p2} C {q2} |
| q2 Ù B Þ p2 |
| q2 Ù ¬ B Þ q1 |
Celles-ci découlent de la sémantique des processus de la section 5.4.2 par une simple
abstraction (voir [Cou90] en particulier).
Par exemple (voir [Win93]), le système suivant est un système
d'assertions correctes:
{ x=x0 et y=y0 }
q = 0;
while (x >= y) {
{x=x0-qy0 et y=y0}
q = q+1;
{x=x0-(q-1)y0 et y=y0}
x = x-y;
{x=x0-qy0 et y=y0}
}
{x=x0-qy0 et x<y et y=y0}
Une fois la preuve faite séquentiellement, il faut prouver que les invariants
trouvés pour chaque thread pris séparément, sont encore valides si
tout ou partie d'autres threads s'exécutent entre deux instructions, modifiant
ainsi l'état local du thread! Cela s'appelle la preuve de non-interférence.
Attention car on suppose ici que les affectations sont atomiques (ce sera
vrai en JAVA dans la suite pour les affectations de constantes, ce qui sera
le seul cas intéressant pour nous; sinon il faudrait décomposer les
affectations en load, store etc. comme expliqué précédemment).
Pour que cela puisse se faire de façon correcte, il faut introduire des
variables nouvelles dans le code séquentiel, qui déterminent le point
de contrôle auquel le processus est arrivé. Sans cela, la méthode est
fausse (en fait, l'article d'origine de S. Owicki et de D. Gries comportait
cet oubli). Par exemple, on devrait transformer la preuve précédente
en:
{ x=x0 et y=y0 et c=0}
q = 0;
{ x=x0 et y=y0 et c=1}
while (x >= y) {
{x=x0-qy0 et y=y0 et c=2}
q = q+1;
{x=x0-(q-1)y0 et y=y0 et c=3}
x = x-y;
{x=x0-qy0 et y=y0 et c=4}
}
{x=x0-qy0 et x<y et y=y0 et c=5}
c représente le point de contrôle courant, numéroté de façon
fort logique de 1 à 5 ici.
On va donc supposer que chaque thread Pi parmi P1,...,Pk a un compteur
ci et des assertions Ai,k avant les instructions
Ii,k de Pi (pour k variant sur l'ensemble
des points de contrôle de Pi) utilisant éventuellement des prédicats
aussi sur les autres compteurs ordinaux
c1,...,ck. Alors il faut vérifier les conditions dites
de non-interférences suivantes, quand Ij,l est une affectation x=u:
{ (Ai,k Ù Aj,l)[x¬ u] } Ij,l {Ai,k}
On peut simplifier un peu cela dans le cas qui nous préoccupe, car
on n'a qu'une affectation sur un objet partagé, donc on n'a pas besoin de numéroter
toutes les instructions.
Introduisons deux variables auxiliaires after[0] et
after[1] (qui servent à
indiquer si le contrôle est après turn=t
dans le code).
Rajoutons également les instructions after[0]=true,
after[1]=true après respectivement turn=0 et turn=1.
En utilisant l'abbréviation I= [turn=1 ou turn=2] on commente le code
avec les assertions comme à la figure 6.11.
{ non flag[0] }
flag[0]=true; after[0]=false;
{ flag[0] et non after[0] }
turn=0; after[0]=true;
{ inv: flag[0] et after[0] et I }
while (flag[1] && (turn==0))
{ flag[0] et after[0] et I }
Thread.yield();
{ flag[0] et after[0] et (flag[1] et (non(after[1]) ou turn=1)) }
[ Section Critique CS1]
{ flag[0] }
flag[0]=false;
|
Figure 6.11: Assertions pour la preuve de l'algorithme de Peterson.
De même pour le deuxième processus, à la figure 6.12.
{ non flag[1] }
flag[1]=true; after[1]=false;
{ flag[1] et non after[1] }
turn=1; after[1]=true;
{ inv: flag[1] et after[1] et I }
while (flag[0] && (turn==0)) do
{ flag[1] et after[1] et I }
Thread.yield();
{ flag[1] et after[1] et (flag[0] et (non(after[0]) ou turn=0)) }
[ Section Critique CS2]
{ flag[1] }
flag[1]=false;
|
Figure 6.12: Assertions pour la preuve de l'algorithme de Peterson.
Il est relativement aisé de se convaincre que ces assertions forment
bien un schéma de preuve correct de chacun des processus pris séquentiellement.
Seule subsiste la preuve de non-interférence.
En fait, seul,
pre(CS1) = flag[0] et after[0] et (flag[1] et (non(after[1])
ou (turn=1)))
contient des références à des objets manipulés par l'autre processus, et ce,
seulement en les lignes
flag[1]=true; after[1]=false;
et
turn=1; after[1]=true;
Or,
{ pre(CS1) } flag[1]=true; after[1]=false; { pre(CS1) }
et
{ pre(CS1) } turn=1; after[1]=true; { pre(CS1) }
et de même par symétrie.
De plus, on peut voir que
pre(CS1) et pre(CS2) implique (turn=0 et turn=1)
Ce qui implique que l'on a toujours
non(pre(CS1) et pre(CS2))
prouvant ainsi l'exclusion mutuelle.
Remarquez qu'il existe une
généralisation de l'algorithme de Peterson à n processeurs.
C'est le programme de la figure 6.13, codé sur chacun des n processeurs (liste[0] à liste[nproc-1]).
public class PetersonN extends ExclusionMutuelle
{
public PetersonN(int nb) {
int i;
nproc = nb;
turn = new int[nproc-1];
flag = new int[nproc];
for (i=0; i < nproc; i++) {
flag[i] = -1; }
}
public void Pmutex(int t) {
int j, k;
boolean cond;
for (j=0; j < nproc-1; j++) {
flag[t] = j;
turn[j] = t;
cond = true;
for (k=0; (k < nproc) && (k != t); k++)
cond = cond || (flag[k] >= j);
while (cond && (turn[j] == t))
Thread.yield();
}
}
public void Vmutex(int t) {
flag[t] = -1;
}
private volatile int[] turn;
private int nproc;
private volatile int[] flag;
}
|
Figure 6.13: Algorithme de Peterson pour plus de deux tâches.
Il faut évidemment légèrement changer le programme de test (ici pour 5 tâches), voir
figure 6.14.
public class TestN
{
public final static int nb = 5;
public static void main(String args[]) {
int i;
Tache[] liste;
liste = new Tache[nb];
ExclusionMutuelle alg = new PetersonN(nb);
for (i=0; i < nb; i++) {
liste[i] = new Tache("Tache "+i,i,alg);
liste[i].start();
}
}
}
|
Figure 6.14: Classe pour tester des algorithmes d'exclusion mutuelle pour plus de deux processus.
En fait c'est la solution pour 2 processeurs itérée n-1 fois.
flag[i]=-1 signifie que liste[i] ne s'engage pas en section critique.
turn permet de gérer les conflits dans un couple de processus.
Cet algorithme réalise bien l'exclusion mutuelle
sans interblocage
et avec équité.
Dans les améliorations possibles, il y a en particulier
l'algorithme de Burns (1981). C'est une solution entièrement symétrique
qui minimise
le nombre de variables utilisées ainsi que les valeurs qu'elles peuvent
prendre en cours de programme.
Chapter 7 Problèmes d'ordonnancement
7.1 Introduction
Revenons à la mémoire partagée... et aux PRAM!
Le problème important qui va nous préoccuper dans ce chapitre est
de paralléliser ce qui a priori prend le plus de temps dans un programme: les nids de boucle.
Nous n'irons pas jusqu'à traiter la façon dont un compilateur va effectivement
paralléliser le code, mais on va au moins donner un sens à ce
qui est intrinsèquement séquentiel, et à ce qui
peut être calculé en parallèle.
Avant de commencer, expliquons en quoi ceci est primordial, pour l'efficacité d'un
programme parallèle.
Supposons qu'après parallélisation, il reste une proportion de s (0 < s £ 1) de notre code qui soit séquentiel,
et qu'il s'exécute sur
p processeurs. Alors
l'accélération du calcul complet par rapport à
un calcul séquentiel sera au maximum de,
(maximum de 1/s pour s fixé); c'est la loi d'Amdahl.
Conséquence:
si on parallélise 80 pour cent d'un code (le reste étant séquentiel),
on ne pourra jamais dépasser, quelle que soit la machine cible, une accélération
d'un facteur 5!
7.2 Nids de boucles
Un nid de boucles est une portion de code dans laquelle on trouve un certain nombre de boucles imbriquées.
Le cas le plus simple de nid de boucles est le nid de boucles parfait, qui a la propriété
que les corps de boucle sont inclus dans exactement les mêmes boucles.
Par exemple, le code plus bas est un nid de boucles:
for (i=1;i<=N;i++) {
for (j=i;j<=N+1;j++)
for (k=j-i;k<=N;k++) {
S1;
S2;
}
for (r=1;r<=N;r++)
S3;
}
Par contre, ceci n'est pas un nid de boucles parfait:
S1 et S2 sont englobées par les boucles i, j et k
alors que S3 est englobée par les boucles i et r.
Dans le cas de nids de boucles parfaits, on peut définir aisément l'instance
des instructions du corps de boucle, qui est exécutée à un moment donné.
Ceci se fait à travers la notion de vecteurs d'itération.
Ceux-ci sont des vecteurs
de dimension
n (n étant le nombre de boucles imbriquées),
dont les composantes décrivent les valeurs des indices pour chacune des boucles.
Pour les nids de boucles non-parfaits, les domaines d'itérations sont incomparables a priori.
Il suffit de ``compléter'' les vecteurs d'itération de façon cohérente: I ® I
Par exemple, pour S3 on a un vecteur d'itération en (i,r) dont le domaine
est 1 £ i, r £ N.
Pour S1 on a un vecteur d'itération en (i,j,k) dont le domaine est
1 £ i £ N, i £ j £ N+1 et j-i £ k £ N.
On note une instance de S à l'itération I, S(I).
On supposera dans la suite de ce chapitre que les domaines d'itération forment des polyèdres
(conjonction d'inégalités linéaires).
On définit également l'ordre séquentiel d'exécution
qui décrit l'ordre d'exécution ``par défaut''. Ceci se définit de façon triviale,
comme un ordre <seq entre les instructions, quand on n'a pas de boucles. C'est l'ordre
textuel <text.
En présence de boucle, on utilise en plus la notion de vecteur d'itération: une instance d'une
instruction T au vecteur d'itération I,
T(I), sera exécutée avant son instance au vecteur d'itération J, c'est à dire
T(I) <seq T(J) si I <lex J où
est <lex est l'ordre lexicographique. De façon plus générale, on définit:
| S(I) <seq T(J) |
Û |
|
| |
(I <seq J) ou |
| |
(I = J et S <text T) |
A partir de là, on veut mettre en parallèle certaines instructions:
une partie de l'ordre séquentiel que l'on vient de définir est à
respecter absolument, une autre pas (permutation possible d'actions).
On va définir un ordre partiel (dit de Bernstein), qui est l'ordre minimal
à respecter pour produire un code
sémantiquement équivalent à l'ordre initial.
En fait, l'ordre séquentiel va être une extension de l'ordre partiel de Bernstein.
Cet ordre partiel est défini à partir de 3 types de dépendances de données: flot, anti et sortie.
7.3 Dépendance des données
7.3.1 Définitions
On va en définir de trois sortes: flot, anti et sortie,
toujours dirigées par l'ordre séquentiel. C'est à dire que si S(I) <seq T(J), on
a une:
-
Dépendance de flot de S(I) vers T(J): si un emplacement mémoire commun est en écriture
pour S(I) et en lecture pour T(J)
- Dépendance anti de S(I) vers T(J): si un emplacement mémoire commun est en lecture pour
S(I) et en écriture pour T(J)
- Dépendance de sortie de S(I) vers T(J): si un emplacement mémoire commun est en écriture pour
S(I) et en écriture pour T(J)
Prenons l'exemple du programme suivant:
for (i=1;i<=N;i++)
for (j=1;j<=N;j++)
a(i+j) = a(i+j-1)+1;
Son graphe de dépendances, est donné à la figure 7.1. Les dépendances
de flot sont représentées par les flèches pleines. Les dépendances anti et de sortie
sont représentées par des flèches à traits pointillés.
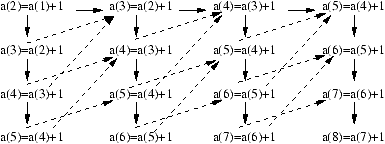
Figure 7.1: Dépendances flot, anti et de sortie.
7.3.2 Calcul des dépendances
Supposons que S(I) et T(J) accèdent au même tableau a (S en écriture, T en lecture par exemple, pour la
dépendance de flot)
S(I): a(f(I))=... et T(J): ...=a(g(J));
l'accès au tableau est commun si f(I)=g(J).
Si f et g sont des fonctions affines à coefficients entiers cela peut se tester algorithmiquement
en temps polynomial.
Chercher une dépendance de flot par exemple, revient à prouver en plus S(I) <seq T(J).
Encore une fois, cela se fait en général par la résolution de systèmes d'égalités et d'inégalités
affines.
Chercher les dépendances directes (c'est-à-dire celles qui engendrent par transitivité
toutes les dépendances) est bien plus compliqué. Cela peut se faire
par programmation linéaire, par des techniques
d'optimisation dans les entiers etc.
Nous n'allons pas dans ce chapitre décrire ces algorithmes. Nous nous contenterons
de montrer quelques exemples.
Prenons f(I)=i+j et g(J)=i+j-1 (ce sont les fonctions d'accès au tableau a dans
l'exemple plus haut). On cherche les dépendances entre l'écriture S(i',j') et la lecture T(i,j):
-
f(I)=g(J) Û i'+j'=i+j-1
- S(i',j') <seq S(i,j) Û ( (i'£ i-1) ou (i=i' et
j'£ j-1) )
Pour déterminer une dépendance de flot directe, on doit résoudre:
max<seq {(i',j') | (i',j') <seq (i,j), i'+j'=i+j-1, 1 £ i,i',j,j' £ N }
La solution est:
| (i,j-1) |
si j ³ 2 |
| (i-1,j) |
si j=1 |
Pour déterminer une antidépendance directe de S(i,j) vers S(i',j'), on doit résoudre:
min<seq {(i',j') | (i,j) <seq (i',j'), i'+j'=i+j-1, 1 £ i,i',j,j' £ N }
La solution (pour j³ 3, i£ N-1) est:
(i+1,j-2)
7.3.3 Approximation des dépendances
Les dépendances sont en général bien trop ardues à déterminer exactement. On s'autorise
donc à n'obtenir que des informations imprécises, mais correctes. L'une d'elles est le
Graphe de Dépendance Etendu (ou GDE):
-
Sommets: instances Si(I), 1 £ i £ s et I Î DSi
- Arcs: S(I) ® T(J) pour chaque dépendance
On appelle ensemble des paires de dépendances entre S et T l'ensemble suivant:
{(I,J) | S(I) ® T(J)} Í ZZnS × ZZnT
L'ensemble de distance de ces dépendances est:
{ (J-I) | S(I) ® T(J) } Í ZZnS,T
Dans le cas de l'exemple de la section 7.3.1, on a des paires:
-
lecture a(i+j-1)-écriture a(i+j): ensemble de distance {(1,-2)}
- écriture a(i+j)-lecture a(i+j-1): ensemble de distance {(1,0),(0,1)}
- écriture a(i+j)-écriture a(i+j): ensemble de distance {(1,-1)}
Il reste un problème de taille: on ne peut pas calculer le GDE à la compilation!
(de toutes façons, il est encore bien trop gros)
On doit donc abstraire encore un peu plus.
On peut définir le Graphe de Dépendance Réduit
ou GDR:
-
Sommets: instructions Si (1 £ i £ s)
- Arcs: e: S ® T si il existe au moins un arc S(I) ® T(J) dans le GDE
- Etiquette: w(e) décrivant un sous-ensemble De de ZZnS,T
Le tri topologique du GDR permet d'avoir une idée des portions séquentielles, et des
portions parallélisables.
On peut encore abstraire ce GDR en étiquetant ses arcs.
Par exemple, on peut utiliser des niveaux de dépendance, que l'on définit plus bas,
et on obtiendra le Graphe de Dépendance
Réduit à Niveaux (GDRN).
On dit qu'une dépendance entre S(I) et T(J) est boucle indépendante si elle a lieu au cours d'une même
itération des boucles englobant S et T; sinon on dit qu'elle est portée par la boucle.
On étiquette en conséquence les arcs e: S ® T du GDR, par la fonction d'étiquetage l:
-
l(e)=¥ si S(I)® T(J) avec J - I=0
- l(e) Î [1,nS,T] si S(I) ® T(J), et la première composante non nulle
de J-I est la l(e)ieme composante
Prenons un exemple:
for (i=2;i<=N;i++) {
S1: s(i) = 0;
for (j=1;j<i-1;j++)
S2: s(i) = s(i)+a(j,i)*b(j);
S3: b(i) = b(i)-s(i);
}
Le GDRN est représenté à la figure 7.2 (où a signifie dépendance anti, o de sortie et f de
flot).
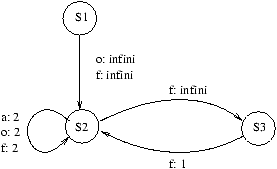
Figure 7.2: GDRN
Les vecteurs de direction sont une autre abstraction, en particulier
de ces ensembles de distance:
-
on note z+ pour une composante si toutes les distances sur cette composante ont au moins la valeur z
- on note z- pour une composante si toutes les distances sur cette composante ont au plus la valeur z
- on note + à la place de 1+, - à la place de -1-
- on note * si la composante peut prendre n'importe quelle valeur
- on note z si la composante a toujours la valeur z
On obtient comme GDRV celui de la figure 7.3
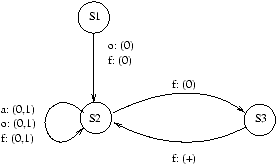
Figure 7.3: GRDV
7.4 Transformations de boucles
C'est là ce qui permet effectivement
de paralléliser, à partir d'une connaissance minimale des dépendances: certaines dépendances
autorisent à transformer localement le code, qui est à son tour bien plus parallélisable.
Il existe deux types
d'algorithmes bien connus:
-
Allen et Kennedy (basé sur le GDRN) : effectue des distributions de boucles
- Lamport : transformations unimodulaires (basé sur le GDRV), c'est à dire, torsion, inversion et permutation de boucles
On décrira un peu plus loin l'algorithme d'Allen et Kennedy. Pour celui de Lamport, on reportera
le lecteur à [RL03]. Avant d'expliquer comment on extrait d'un graphe de dépendance
l'information nécessaire à la parallélisation, on commence par expliquer quelles sont les
grands types de transformation (syntaxique) de code. Cela nous
permettra de paralléliser un petit code, à la main, sans recourir à
un algorithme de parallélisation automatique.
7.4.1 Distribution de boucles
Toute instance d'une instruction S peut être exécutée avant toute instance de T si on n'a jamais
T(J) ® S(I) dans le GDE.
Plusieurs cas sont à considérer, pour le code:
for (i=...) {
S1;
S2;
}
Cas 1:
S1 ® S2 mais on n'a pas de dépendance de S2 vers S1, alors on peut transformer le code en:
for (i=...)
S1;
for (i=...)
S2;
Cas 2:
S2 ® S1 mais on n'a pas de dépendance de S1 vers S2, alors on peut transformer le code en:
for (i=...)
S2;
for (i=...)
S1;
7.4.2 Fusion de boucles
On transforme (ce qui est toujours possible):
forall (i=1;i<=N;i++)
D[i]=E[i]+F[i];
forall (j=1;j<=N;j++)
E[j]=D[j]*F[j];
en:
forall (i=1;i<=N;i++)
{
D[i]=E[i]+F[i];
E[i]=D[i]*F[i];
}
Cela permet une vectorisation et donc une
réduction du coût des boucles parallèles, sur certaines architectures.
7.4.3 Composition de boucles
De même, on peut toujours transformer:
forall (j=1;j<=N;j++)
forall (k=1;k<=N;k++)
...
en:
forall (i=1;i<=N*N;i++)
...
Cela permet de changer l'espace d'itérations (afin d'effectuer éventuellement
d'autres transformations).
7.4.4 Echange de boucles
Typiquement, on transforme:
for (i=1;i<=N;i++)
for (j=2;j<=M;j++)
A[i,j]=A[i,j-1]+1;
en la boucle avec affectation parallèle:
for (j=2;j<=M;j++)
A[1:N,j]=A[1:N,j-1]+1;
Ce n'est évidemment possible que dans certains cas.
7.4.5 Déroulement de boucle
Typiquement, on transforme:
for (i=1;i<=100;i++)
A[i]=B[i+2]*C[i-1];
en:
for (i=1;i<=99;i=i+2)
{
A[i]=B[i+2]*C[i-1];
A[i+1]=B[i+3]*C[i];
}
7.4.6 Rotation de boucle [skewing]
C'est le pendant du changement de base dans l'espace des vecteurs d'itération. Typiquement:
for (i=1;i<=N;i++)
for (j=1;j<=N;j++)
a[i,j]=(a[i-1,j]+a[i,j-1])/2;
Il y a un front d'onde, et on peut le transformer en:
for (k=2;k<=N;k++)
forall (l=2-k;l<=k-2;l+=2)
a[(k-l)/2][(k+l)/2] = a[(k-l)/2-1][(k+l)/2]+a[(k-l)/2][(k+l)/2-1];
for (k=1;k<=N;k++)
forall (l=k-N;l<=N-k;l+=2)
a[(k-l)/2][(k+l)/2] = a[(k-l)/2-1][(k+l)/2]+a[(k-l)/2][(k+l)/2-1];
7.4.7 Exemple de parallélisation de code
On considère la phase
de remontée après une décomposition LU d'une matrice.
Soit donc à résoudre le système triangulaire supérieur
Ux=b
avec,
| U= |
æ
ç
ç
ç
è |
| U1,1 |
U1,2 |
U1,3 |
··· |
U1,n |
| 0 |
U2,2 |
U2,3 |
··· |
U2,n |
| |
|
|
··· |
|
| 0 |
0 |
··· |
0 |
Un,n |
|
ö
÷
÷
÷
ø |
On procède par ``remontée'' c'est à dire que l'on
calcule successivement,
pour i=n-1,n-2,···,1.
Le code séquentiel correspondant est:
x[n]=b[n]/U[n,n];
for (i=n-1;i>=1;i--)
{
x[i]=0;
for (j=i+1;j<=n;j++)
L: x[i]=x[i]+U[i,j]*x[j];
x[i]=(b[i]-x[i])/U[i,i];
}
Son graphe de dépendances est donné à la figure 7.4, où on a essentiellement
représenté les dépendances de flot.
Il est à noter qu'il y a aussi des anti-dépendances
des itérations (i,j) vers (i-1,j).
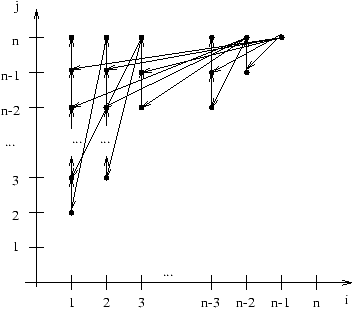
Figure 7.4: Graphe de dépendances de la remontée LU
En faisant une rotation et une distribution de boucles on arrive à paralléliser cet
algorithme en:
H': forall (i=1;i<=n-1;i++)
x[i]=b[i];
T': x[n]=b[n]/U[n,n];
H: for (t=1;t<=n-1;t++)
forall (i=1;i<=n-t;i++)
L: x[i]=x[i]-x[n-t+1]*U[i],n-t+1];
T: x[n-t]=x[n-t]/U[n-t,n-t];
Le ratio d'accélération est de l'ordre de n/4 asymptotiquement.
7.5 Algorithme d'Allen et Kennedy
Le principe est de
remplacer certaines boucles for par des boucles forall
et d'utiliser la distribution de boucles pour diminuer le nombre d'instructions dans les boucles, et donc
réduire les dépendances.
L'algorithme est le suivant:
-
Commencer avec k=1
- Supprimer dans le GDRN G toutes les arêtes de niveau inférieur à k
- Calculer les composantes fortement connexes (CFC) de G
- Pour tout CFC C dans l'ordre topologique:
-
Si C est réduit à une seule instruction S sans arête, alors générer des boucles
parallèles dans toutes les dimensions restantes (i.e. niveaux k à nS) et générer le code pour S
- Sinon, l=lmin(C), et générer des boucles parallèles du niveau k au niveau l-1, et une boucle
séquentielle pour le niveau l. Puis reboucler l'algorithme avec C et k=l+1
Pour illustrer cet algorithme, on va prendre l'exemple suivant:
for (i=1;i<=N;i++)
for (j=1;j<=N;i++) {
S1: a(i+1,j+1) = a(i+1,j)+b(i,j+2);
S2: b(i+1,j) = a(i+1,j-1)+b(i,j-1);
S3: a(i,j+2) = b(i+1,j+1)-1;
}
On trouve les dépendances suivantes:
-
Flot S1 ® S1, variable a, distance (0,1),
- Flot S1 ® S2, variable a, distance (0,2),
- Flot S2 ® S1, variable b, distance (1,-2),
- Flot S2 ® S2, variable b, distance (1,1),
- Anti S1 ® S3, variable a, distance (1,-2),
- Anti S2 ® S3, variable a, distance (1,-3),
- Anti S3 ® S2, variable b, distance (0,1),
- Sortie S1 ® S3, variable a, distance (1,-1).
Ce qui donne le GDRN de la figure 7.5.
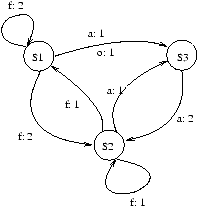
Figure 7.5: GDRN
Ce GDRN est fortement connexe et a des dépendances de niveau 1.
La boucle sur i sera donc séquentielle.
On enlève maintenant les dépendances de niveau 1 pour obtenir le
GDRN modifié de la figure 7.6.
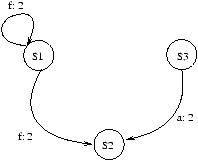
Figure 7.6: GDRN
La parallélisation finale est ainsi:
for (i=1;i<=N;i++) {
for (j=1;j<=N;j++)
S1: a(i+1,j+1) = a(i+1,j)+b(i,j+2);
forall (j=1;j<=N;j++)
S3: a(i,j+2) = b(i+1,j+1)-1;
forall (j=1;j<=N;j++)
S2: b(i+1,j) = a(i+1,j-1)+b(i,j-1);
}
Chapter 8 Communications et routage
8.1 Généralités
On distingue généralement les
topologies statiques où le réseau d'interconnexion est fixe, en
anneau, tore 2D,
hypercube, graphe complet etc.
des topologies dynamiques, modifiées en cours d'exécution (par configuration
de switch).
Chaque topologie de communication a des
caractéristiques spécifiques, qui permettent de discuter de leurs qualités et de
leurs défauts. Ces caractéristiques sont, en fonction du nombre de processeurs interconnectés,
le degré du graphe d'interconnection, c'est-à-dire le nombre de processeurs interconnectés
avec un processeur donné, le diamètre, c'est-à-dire la distance maximale entre deux noeuds,
et le nombre total de liens, c'est-à-dire le nombre total de ``fils'' reliant les différents
processeurs. Les topologies de communications avec un petit nombre de liens sont plus économiques mais
en général leur diamètre est plus important, c'est-à-dire que le temps de communication
entre deux processeurs ``éloignés'' va être plus important. Enfin, on verra un peu plus loin
que le degré est également une mesure importante: cela permet d'avoir plus de choix pour
``router'' un message transitant par un noeud. On imagine bien également (thème développé
au chapitre 11, mais sous un autre point de vue), que si on a une panne au niveau d'un
lien, ou d'un processeur, plus le degré est important, plus on pourra trouver un autre chemin
pour faire transiter un message. Les caractéristiques de quelques topologies statiques classiques
sont résumées dans le tableau ci-dessous:
| Topologie |
# proc. |
do |
diam. |
# liens |
| Complet |
p |
p-1 |
1 |
p(p-1)/2 |
| Anneau |
p |
2 |
ë p/2 û |
p |
| Grille 2D |
sqrt(p)sqrt(p) |
2,3,4 |
2(sqrt(p)-1) |
2p-2sqrt(p) |
| Tore 2D |
sqrt(p)sqrt(p) |
4 |
2 ë sqrt(p)/2 û |
2p |
| Hypercube |
p=2d |
d=log(p) |
d |
p log(p)/2 |
L'intérêt est relatif, pour chaque choix. Par exemple, le
réseau complet est idéal pour le temps de communications (toujours unitaire)
mais le passage à l'échelle est difficile! (prix du cablage, comment rajouter des
nouveaux processeurs?).
La topologie en anneau n'est pas chère, mais les communications sont lentes,
et la tolérance aux pannes
des liens est faible.
On considère généralement que le tore 2D ou l'hypercube sont de bons compromis entre ces deux architectures.
8.2 Routage
On distingue deux modèles principaux, pour le routage des messages dans un système distribué.
Chaque modèle a un calcul de coût de communication distinct.
Le premier modèle est le modèle ``Store and Forward'' (SF):
chaque processeur intermédiaire reçoit et stocke le message M
avant de le re-émettre en direction du processeur destinataire. C'est un
modèle à commutation de message
qui équipait les premières générations de machines.
Le coût de communication est de d(x,y)(b+Lt) (où d(x,y) est la distance
entre les machines x et y, t est lié au débit du réseau, b est la
latence d'un envoi de message, et L est la longueur du message)
sauf programmation particulièrement optimisée (voir
section 8.3.5) où on peut atteindre Lt + O(sqrt(L)).
Le modèle ``cut-through'' (CT) utilise un
co-processeur de communication associé à chaque noeud.
Le coût de communication est de b+(d(x,y)-1)d+Lt (où d est
encore une fois lié au débit du réseau, t est la latence).
Si d << b, le chemin est calculé par le matériel, la partie logicielle
étant dans le facteur b.
Il existe également
deux principaux protocoles de routage: ``Circuit-switching'' (CC - ou ``commutation de
données'') et ``Wormhole'' (WH).
Le circuit-switching
crée le chemin avant l'émission des premiers octets. Le message est ensuite
acheminé directement entre source et destinataire. Cela nécessite une
immobilisation des liens (cas par exemple de l'iPSC d'INTEL).
Le protocole Wormhole
place l'adresse du destinataire dans l'entête du message.
Le routage se fait sur chaque processeur et le
message est découpé en petits paquets appelés flits.
En cas de blocage: les flits sont stockés dans les registres internes
des routeurs intermédiaires (exemple, Paragon d'INTEL).
En général,
CC et WH sont plus efficaces que SF. Ils masquent la distance entre les processeurs
communiquants.
CC contruit son chemin avant l'envoi des premiers paquets de données
alors que WH construit sa route tandis que le message avance dans le réseau
(meilleure bande passante que CC). Ces points sont résumés à la figure
8.1.
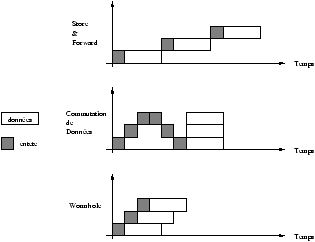
Figure 8.1: Comparaison CC, WH et SF
8.3 Algorithmique sur anneau de processeurs
8.3.1 Hypothèses
On étude une architecture
dans laquelle (voir figure 8.2 pour une explication graphique)
on a p processeurs en anneau,
chacun ayant accès à
son numéro d'ordre (entre 0 et p-1), par my_num()
et au nombre total de processeur par tot_proc_num (=p).
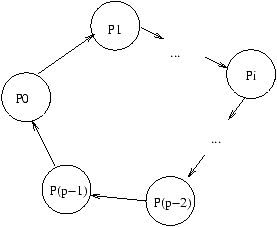
Figure 8.2: Architecture en anneau
En mode SPMD, tous les processeurs exécutent le même code,
ils calculent tous dans leur mémoire locale,
et ils peuvent envoyer un message au processeur de numéro
proc_num()+1[p]
par send(adr,L).
La variable adr contient l'adresse de la première valeur dans la mémoire
locale de l'expéditeur
et L est la longueur du message.
De même, ils peuvent recevoir un message de proc_num()-1[p] par
receive(adr,L).
Le premier problème auquel on est confronté, avant même de penser à implémenter
des algorithmes efficaces, est de s'arranger pour qu'à tout send corresponde un receive.
On peut faire plusieurs hypothèses possibles pour décrire la sémantique de telles primitives.
Les send et receive peuvent être bloquants comme dans OCCAM.
Plus classiquement, send est non bloquant mais receive est bloquant
(mode par défaut en PVM, MPI).
Sur des machines plus modernes, aucune opération n'est
bloquante (trois threads sont utilisés en fait: un pour le calcul, un pour le send et un pour le
receive).
La modélisation du coût d'une communication
est
difficile en général: ici envoyer ou recevoir un message de longueur L (au voisin immédiat) coûtera
b+Lt où
b est le coût d'initialisation (latence) et
t (débit) mesure la vitesse de transmission en régime permanent.
Donc, a priori, envoyer ou recevoir un message de longueur L de
proc_num()+/-q coûtera q(b+Lt). On verra que dans certains cas, on peut
améliorer les performances de communication en ``recouvrant'' plusieurs communications au même
moment (entre des paires de processeurs distincts).
8.3.2 Problème élémentaire: la diffusion
C'est l'envoi par un Pk d'un message de longueur L (stocké à l'adresse adr)
à tous les autres processeurs. C'est une primitive
implémentée de façon efficace dans la plupart des librairies de communications (PVM, MPI etc.).
On va supposer ici que le receive est bloquant.
broadcast(k,adr,L) { // emetteur initial=k
q = my_num();
p = tot_proc_num();
if (q == k)
(1) send(adr,L);
else
if (q == k-1 mod p)
(2) receive(adr,L);
else {
(3) receive(adr,L);
(4) send(adr,L);
}
}
L'exécution est décrite pour k=0 au temps 0
à la figure 8.3,
au temps b+Lt à la figure 8.4, au temps j(b+Lt) (j<p-1)
à la figure 8.5, et au temps (p-1)(b+Lt) à la figure 8.6.
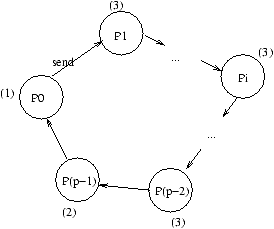
Figure 8.3: Exécution de la diffusion sur un anneau au temps 0.
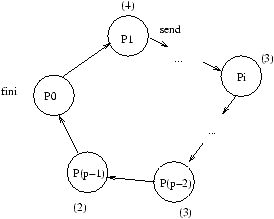
Figure 8.4: Exécution de la diffusion sur un anneau au temps b+Lt.
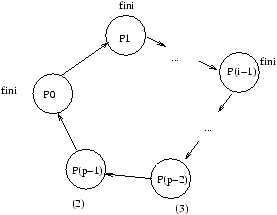
Figure 8.5: Exécution de la diffusion sur un anneau au temps i(b+Lt) (i<p-1).
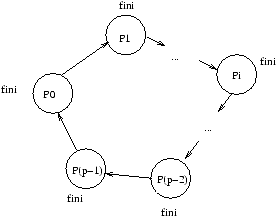
Figure 8.6: Exécution de la diffusion sur un anneau au temps (p-1)(b+Lt).
8.3.3 Diffusion personnalisée
On suppose toujours ici
un send non-bloquant et un receive bloquant.
On veut programmer un envoi par Pk
d'un message différent à tous les processeurs (en adr[q] dans Pk pour
Pq). A la fin, chaque processeur devra avoir son message à la location adr.
L'algorithme suivant opère en pipeline, et on obtient une bonne performance
grâce à un recouvrement entre les différentes communications!
Le programmme est le suivant:
scatter(k,adr,L) {
q = my_num();
p = tot_proc_num();
if (q == k) {
adr = adr[k];
for (i=1;i<p;i=i+1)
send(adr[k-i mod p],L); }
else
(1) receive(adr,L);
for (i=1;i<k-q mod p;i = i+1) {
(2) send(adr,L);
(3) receive(temp,L);
adr = temp; } }
Les exécutions pour k=0 aux temps 0
b+Lt, i(b+Lt) et
enfin (p-1)(b+Lt), sont représentées respectivement aux figures
8.7, 8.8, 8.9 et 8.10.
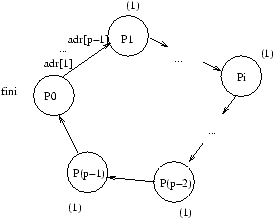
Figure 8.7: Exécution de la diffusion personnalisée au temps 0.
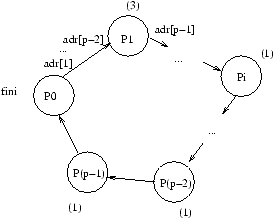
Figure 8.8: Exécution de la diffusion personnalisée au temps b+Lt.
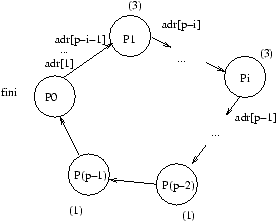
Figure 8.9: Exécution de la diffusion personnalisée au temps i(b+Lt).
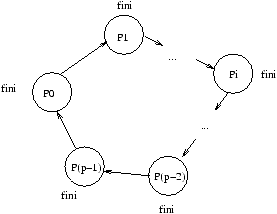
Figure 8.10: Exécution de la diffusion personnalisée au temps (p-1)(b+Lt).
8.3.4 Echange total
Maintenant, chaque processeur k veut envoyer un message à tous les autres.
Au départ chaque processeur dispose de son message à envoyer à tous les autres à la location
my_adr.
A la fin, tous ont un tableau (le même) adr[] tel que adr[q] contient le message
envoyé par le processeur q.
Il se trouve que par la même technique de recouvrement des communications, cela
peut se faire aussi en (p-1)(b+Lt) (et de même pour l'échange total personnalisé,
voir [RL03]).
Le programme est:
all-to-all(my_adr,adr,L) {
q = my_num();
p = tot_proc_num();
adr[q] == my_adr;
for (i=1;i<p;i++) {
send(adr[q-i+1 mod p],L);
receive(adr[q-i mod p],L);
}
}
8.3.5 Diffusion pipelinée
Les temps d'une diffusion simple et d'une diffusion personnalisée sont les mêmes; peut-on améliorer
le temps de la diffusion simple en utilisant les idées de la diffusion personnalisée?
La réponse est oui: il suffit de
tronçonner le message à envoyer en r morceaux (r divise L bien choisi).
L'émetteur envoie successivement les r morceaux, avec recouvrement partiel des communications.
Au début, ces morceaux de messages sont dans adr[1],...,adr[r] du
processeur k.
Le programme est:
broadcast(k,adr,L) {
q = my_num();
p = tot_proc_num();
if (q == k)
for (i=1;i<=r;i++) send(adr[i],L/r);
else
if (q == k-1 mod p)
for (i=1;i<=r;i++) receive(adr[i],L/r);
else {
receive(adr[1],L/r);
for (i=1;i<r;i++) {
send(adr[i],L/r);
receive(adr[i+1],L/r); } } }
Le temps d'exécution se calcule ainsi;
le premier morceau de longueur L/r du message sera arrivé au dernier processeur
k-1 mod p en temps (p-1)(b+L/rt) (diffusion simple).
Les r-1 autres morceaux arrivent les uns derrière les autres, d'où un temps supplémentaire
de (r-1)(b+L/rt).
En tout, cela fait un temps de (p-2+r)(b+L/r t).
On peut maintenant optimiser le paramètre r.
On trouve
ropt=sqrtL(p-2)t/b.
Le temps optimal d'exécution est donc de
Quand L tend vers l'infini, ceci est asymptotiquement équivalent à Lt, le facteur
p devient négligeable!
8.4 Election dans un anneau bidirectionnel
Chaque processeur part avec un
identificateur propre (un entier dans notre cas), et au bout d'un temps fini,
on veut que chaque processeur termine avec l'identificateur d'un même processeur,
qui deviendra ainsi le ``leader''.
Dans la suite, les processeurs vont être organisés en anneau bidirectionnel
synchrone:
-
Les n processeurs sont numérotés de P0 jusqu'à Pn-1. Par abus
de notation, on ne décrira pas les indices des processeurs modulo n. Ainsi,
par exemple, Pn est identifié à P0.
- Chaque processeur
Pi peut envoyer un message send(adr,L,sens) dont le
contenu se trouve dans sa mémoire locale à l'adresse adr, et consiste en
L entiers. La nouveauté est que Pi peut envoyer vers son voisin Pi+1,
en faisant sens=+, mais aussi vers Pi-1, en faisant sens=-.
- De même, la réception s'écrira maintenant recv(adr,L,sens). Un recv(adr,L,+)
sur Pi+1 réceptionnera le message émis par Pi, qui aura fait send(adr,L,+)
(et de façon similaire pour le -).
- On va maintenant supposer que les processus ne connaissent pas leur indice, et donc pas ceux
de leurs voisins non plus. Le processeur Pi n'a au départ dans sa mémoire locale qu'un entier
pidi représentant son identificateur, et un autre entier leader initialement à zéro.
Chaque pidi est unique, c'est-à-dire que
pidi=pidj implique i=j. Le but de l'algorithme d'élection est qu'un seul processus termine
avec leader=1.
- On prend une hypothèse d'exécution synchrone: tous les codes seront écrits en mode SPMD,
c'est-à-dire que le même code sera exécuté par tous les processeurs, et tous les send
(respectivement recv) seront exécutés exactement au même moment, que l'on appellera
étape: pour simplifier, on ne comptera que le nombre de recv. Un processeur est à l'étape k s'il
a effectué exactement k recv.
Cela implique donc
que ni les send ni les recv ne sont bloquants, par contre, si on n'a envoyé aucun
message à un processus Pi, alors recv fait sur Pi renverra le booléen faux (false),
sinon, il renvoie le booléen vrai (true).
8.4.1 Algorithme de Le Lann, Chang et Roberts (LCR)
Dans cet algorithme, chaque processeur va essentiellement essayer de diffuser son identificateur aux autres processus. Le processus
ayant l'identificateur le plus grand deviendra leader.
Les messages doivent tous transiter dans le même sens, soit +, soit -.
Au lieu de faire une diffusion complète, on peut s'arranger pour que quand un processus reçoit un identificateur,
il le compare avec le sien: si celui qu'il a reçu
est strictement plus grand que le sien, il continue à le passer sur le réseau. S'il est égal à
son identificateur, il se déclare leader, sinon il ne fait rien.
On enlève ainsi certaines communications inutiles.
Chaque processus fait:
LCR() {
send(pid,1,+);
while (recv(newpid,1,+)) {
if (newpid==pid)
leader = 1;
else if (newpid>pid)
send(newpid,1,+);
}
}
Cet algorithme permet bien d'élire un leader. En effet,
soit imax le numéro du processeur ayant l'identificateur pidimax maximal.
Soit 0 £ r £ n-1. On peut voir facilement par induction sur r que après r étapes,
la valeur de newpid sur le processeur Pimax+r est pidimax.
Ainsi, à l'étape n, Pimax+n=Pimax aura reçu son numéro
d'identificateur et en déduira qu'il est le leader.
Il faut maintenant voir que personne d'autre ne croit être le leader.
On peut voir par induction sur r que pour toute étape r, pour tous i et j, si i ¹ imax
et imax £ j < i, alors Pj envoie un message différent de pidi.
Alors nécessairement, seul Pimax peut recevoir son propre identificateur, et est donc le
seul leader possible.
Il faut n étapes et O(n2) communications.
Remarquez que l'on peut
relâcher l'hypothèse synchrone et se contenter d'un send non bloquant et d'un
recv bloquant, sans aucun changement dans l'algorithme.
8.4.2 Algorithme de Hirschberg et Sinclair (HS)
Cet algorithme fonctionne informellement de la façon suivante:
-
Chaque processeur Pi opère par phases, que l'on numérote à partir de 0.
- A chaque phase l, le processeur Pi envoie des tokens contenant son identificateur
dans les deux sens possibles, sur l'anneau.
- Ceux-ci vont parcourir une distance (nombre de noeuds traversés sur l'anneau)
de 2l au maximum (sous-phase d'envoi), avant d'essayer de revenir à leur emetteur Pi (sous-phase
de retour).
- Si les deux tokens reviennent, Pi continue avec la phase l+1.
- Quand l'identificateur pidi, émis par Pi, est dans la sous-phase d'envoi, et est réceptionné
par Pj, alors,
-
si pidi < pidj alors Pj ne fait rien,
- si pidi > pidj alors Pj continue à renvoyer (dans la sous-phase envoi ou retour, selon
la distance déjà effectuée par le message pidi) le token contenant pidi,
- si pidi = pidj alors Pj devient leader.
- Dans la sous-phase retour, tous les processeurs relaient les tokens normalement.
Les tokens utilisés dans cet algorithme contiennent un identificateur, mais aussi un drapeau indiquant
si le message est dans la phase envoi ou dans la phase retour, et un compteur (entier), indiquant
la distance qu'il reste à parcourir dans la phase envoi avant de passer à la phase retour.
On n'essaiera pas de coder ces tokens, et on se contentera d'utiliser les fonctions (que l'on supposera
programmées par ailleurs) suivantes:
-
les tokens sont représentés par une classe JAVA token contenant un constructeur
token(int phase, int message) (phase est le numéro de phase à la création du token);
on supposera qu'un token est de taille L donnée,
- token incr(token x) incrémente la distance parcourue par le token x,
- boolean retour(token tok) renvoie true si le message encapsulé
dans tok a fini la sous-phase envoi, false sinon (par rapport au numéro de phase
encapsulé),
- int valeur(token x) renvoie le message (entier) encapsulé par le token x.
Le pseudo-code correspondant, pour l'algorithme HS, est alors:
HS() {
boolean leader, continuephase;
int l;
token plus, moins;
l = 0;
leader = false;
continuephase = true;
while (continuephase) {
send(token(l,pid),L,+);
send(token(l,pid),L,-);
continuephase = false;
while () {
if (recv(plus,L,+)) {
if (not retour(plus)) {
if (valeur(plus) > pid) {
plus = incr(plus);
if (retour(plus))
send(plus,L,-);
else
send(plus,L,+);
}
else if (valeur(plus) == pid) {
leader = true;
System.exit(0);
}
}
else
if (valeur(plus) == pid) {
l = l+1;
continuephase = true;
}
else
send(incr(plus),L,-);
if (recv(moins,L,-)) {
if (not retour(moins)) {
if (valeur(moins) > pid) {
plus = incr(moins);
if (retour(moins))
send(moins,L,+);
else
send(moins,L,-);
}
else if (valeur(moins) == pid) {
leader = true;
System.exit(0);
}
}
else
if (valeur(moins) == pid) {
l = l+1;
continuephase = true;
}
else
send(incr(moins),L,+);
}
}
}
Le nombre total de phases exécutées au maximum avant qu'un leader ne soit élu est évidemment
borné par 1+é log n ù, car si on a un processeur qui arrive à l'étape é log n ù,
il est nécessaire que son pid soit plus grand que tous les autres, comme 2é log n ù³ n.
Le temps mis par cet algorithme est donc de O(n). En effet, chaque phase l coûte au plus 2l+1
(c'est le nombre de recv maximum que l'on peut avoir dans cette phase, en même temps
par tous les processeurs impliqués dans cette phase). En sommant sur les O(log n) phases, on trouve O(n).
A la phase 0, chaque processus envoie un token dans chaque direction à la distance 1. Donc au maximum, il y a 4n messages
à cette phase (2n aller, et 2n retour).
Pour une phase l > 0, un processus envoie un token seulement si
il a reçu un des deux tokens qu'il a envoyés à la phase l-1. Ce n'est le cas que si il n'a pas trouvé
de processeur de pid supérieur à une distance au maximum de 2l-1, dans chaque direction sur l'anneau.
Cela implique que dans tout groupe de 2l-1+1 processeurs consécutifs, un au plus va commencer une phase l.
Donc on aura au plus
processeurs entrant en phase l. Donc le nombre total de messages envoyés en phase l sera
borné (car chaque token envoyé parcourt au plus 2l processeurs) par:
| 4 |
æ
ç
ç
è |
2l |
ê
ê
ê
ë |
|
|
ú
ú
ú
û |
ö
÷
÷
ø |
£ 8n |
Comme on a un nombre de phases en O(log n), on en déduit un nombre de communications
de l'ordre de
O(n log(n)).
On a moins de communications, et l'algorithme sera meilleur que LCR si le débit des canaux est
faible (moins de contention de messages).
8.5 Communications dans un hypercube
On va examiner successivement les chemins de communication
et en déduire les façon de router les messages dans un hypercube, puis appliquer tout cela au problème du
broadcast dans un hypercube.
8.5.1 Chemins dans un hypercube
Un m-cube est la donnée de
sommets numérotés de 0 à 2m-1.
Il existe une arête d'un sommet à un autre si les deux diffèrent seulement
d'un bit dans leur écriture binaire.
Par exemple, un 2-cube est le carré suivant:
00 ®0 01
¯1 ¯1
10 ®0 11
où les numéros sur les arcs indiquent le numéro du lien (ou du canal) sortant
du noeud correspondant.
Soient A, B deux sommets d'un m-cube, et H(A,B) leur distance de Hamming (le nombre
de bits qui diffèrent dans l'écriture).
Alors il existe un chemin de longueur H(A,B) entre A et B (récurrence
facile sur H(A,B)). En fait,
il existe H(A,B)! chemins entre A et B, dont seuls H(A,B)
sont indépendants (c'est-à-dire qu'ils passent par des sommets différents).
Un routage possible est le suivant. On ``corrige'' les bits de poids faibles d'abord.
Par exemple, pour A=1011, B=1101,
on fait:
A xor B=0110 (ou exclusif bit à bit).
A envoie donc son message sur le lien 1 (c'est à dire vers 1001)
avec en-tête 0100.
Puis 1001, lisant l'entête, renvoie sur son lien 2, c'est à dire
vers 1101=B.
On peut également écrire un algorithme dynamique
qui corrige les bits selon les liens disponibles (voir à ce propos [RL03]).
8.5.2 Plongements d'anneaux et de grilles
Le code de Gray Gm de dimension m est défini récursivement par:
Gm = 0Gm-1 | 1 Gm-1rev
-
xG énumère les éléments de G en rajoutant x en tête de
leur écriture binaire,
- Grev énumère les éléments de G dans l'ordre renversé,
- | est la concaténation (de ``listes'' de mots binaires).
Par exemple:
-
G1={0,1},
- G2={00,01,11,10},
- G3={000,001,011,010,110,111,101,100},
- G4={0000,0001,0011,0010,0110,0111,0101,0100,1100,
1101,1111,1110,1011,1010,1001,1000}.
(imaginer la numérotation des processeurs sur l'anneau, dans cet ordre - un seul
bit change à chaque fois)
L'intérêt des codes de Gray
est qu'ils
permettent de définir un anneau de 2m processeurs dans le m-cube grâce
à Gm. Ils permettent
également de définir un réseau torique de taille 2r × 2s dans un
m-cube avec r+s=m (utiliser le code Gr × Gs).
On trouvera un exemple de plongement d'anneau dans l'hypercube à la figure 8.11.
On reconnaît l'anneau sur l'hypercube à la droite de cette figure, matérialisé
par des arcs gras.
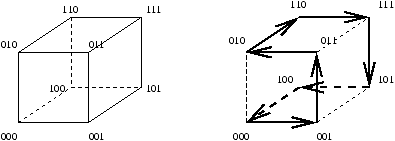
Figure 8.11: Plongement d'un anneau dans un hypercube.
8.5.3 Diffusion simple dans l'hypercube
On suppose que le processeur 0 veut envoyer un message à tous les autres.
Un premier algorithme naïf est le suivant: le processeur 0 envoie à tous ses voisins, puis
tous ses voisins à tous leurs voisins etc.: ceci est très inefficace, car
les messages sont distribués de façon très redondante!
On peut penser à un deuxième algorithme naïf, mais un peu moins: on utilise le code de Gray et on utilise la diffusion
sur l'anneau.
Mais il y a mieux, on va utiliser les
arbres couvrants de l'hypercube.
On se donne les primitives suivantes:
send(cube-link,send-adr,L),
et receive(cube-link, recv-adr,L).
On fait en sorte que
les processeurs reçoivent le message sur le lien correspondant
à leur premier 1 (à partir des poids faibles),
et propagent sur les liens qui précèdent ce premier 1.
Le processeur 0 est supposé avoir un 1 fictif en position m.
Tout ceci va se passer en m phases, i=m-1 ® 0.
En fait, on construit à la fois un arbre couvrant de l'hypercube et l'algorithme
de diffusion (voir la figure 8.12 dans le cas m=4).
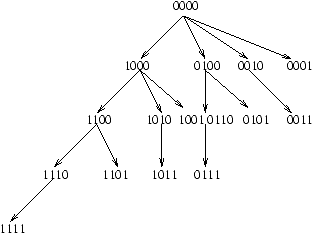
Figure 8.12: Un arbre couvrant pour un 4-cube.
Sans entrer dans les détails, toujours pour m=4, on a les phases suivantes:
-
phase 3: 0000 envoie le message sur le lien 3 à 1000,
- phase 2: 0000 et 1000 envoient le message sur le lien 2, à 0100 et 1100
respectivement,
- ainsi de suite jusqu'à la phase 0.
Pour le cas général, on se reportera à [RL03].
Chapter 9 Remote Method Invocation
Le RMI (Remote Method Invocation) permet d'invoquer des méthodes d'un objet distant, c'est-à-dire
appartenant à une autre JVM, sur une autre machine. Cela permet donc de définir
des
architectures de type client/serveur, comme les
``Remote Procedure Calls'' POSIX.
RMI se rapproche de plus en plus de CORBA (qui est ``indépendant'' du langage), et que l'on
traitera rapidement en fin de chapitre.
Pour plus de détails, on se reportera à [RR]
(duquel on a tiré certains exemples). On pourra
également consulter la page
http://java.sun.com/products/jdk/rmi/.
9.1 Architecture
Une application RMI (ou client/serveur de façon générale) se compose d'un
serveur de méthodes, et de clients. Un serveur est essentiellement une instance
d'une classe ``distante'' que l'on peut référencer
d'une autre machine, et sur laquelle on peut faire agir des méthodes ``distantes''.
Il faut donc définir une
classe qui implémente la méthode distante (serveur),
dont les méthodes renvoient des objets pouvant ``transiter sur le réseau''. Ce sont
les objets instances de classes implémentant l'interface Serializable.
Ce sont des classes dont les objets peuvent
être transcrits en ``stream'', c'est-à-dire en flots d'octets.
La plupart des classes (et de leurs sous-classes) de base
String, HashTable, Vector, HashSet, ArrayList etc. sont Serializable.
On peut aussi ``forcer'' une classe à implémenter Serializable, mais cela est souvent un peu
délicat. Il y a plusieurs méthodes selon les cas, et il faut parfois, dans les cas les plus
difficiles, définir les méthodes:
private void writeObject(ObjectOutputStream aOutputStream) throws IOException;
private void readObject(ObjectInputStream aInputStream)
throws ClassNotFoundException, IOException;
responsables respectivement de décrire un objet sous forme de flot d'octets et de reconstituer l'état
d'un objet à partir d'un flot d'octets.
Dans le cas où on passe une classe Serializable, il faut que la définition de cette
classe soit connue (c'est-à-dire copiée sur les différentes machines, ou accessible par NFS)
des clients et du serveur.
Il peut y avoir à gérer la politique de sécurité (sauf pour les objets ``simples'', comme
String). On en reparlera dans un deuxième temps.
Plus généralement, une méthode d'un serveur peut également renvoyer des objets instances de classes
Remote.
Les classes Remote sont elles des classes dont
les instances sont des objets ordinaires dans l'espace d'adressage
de leur JVM, et pour lesquels
des ``pointeurs'' sur ces objets peuvent être envoyés
aux autres espaces d'adressage.
Il faut également
programmer un ou plusieurs
clients qui utilisent les méthodes distantes et initialisent un
``registre'' d'objets distants (``rmiregistry'') qui associe aux noms d'objets
l'adresse des machines qui les contiennent.
Pour pouvoir compiler séparément (c'est bien nécessaire dans le cas distribué!)
serveurs et clients, il faut définir les interfaces des classes utilisées. Il y a un
certain nombre de fichiers générés par des outils RMI qui vont également se révéler
indispensables.
9.2 Exemple: RMI simple
Prenons un premier exemple, où l'on retourne une valeur Serializable:
il va s'agir d'un
``Hello World'' distribué. On construit les classes de la figure 9.1.
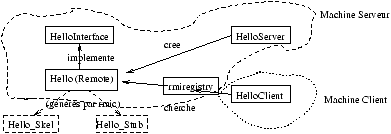
Figure 9.1: Les classes d'un ``Hello World'' distribué''
Définissons d'abord l'interface de l'objet distant:
import java.rmi.*;
public interface HelloInterface extends Remote {
public String say() throws RemoteException;
}
Son unique méthode say est celle qui va afficher à l'écran du client ``Hello World''.
Son implémentation est:
import java.rmi.*;
import java.rmi.server.*;
public class Hello extends UnicastRemoteObject
implements HelloInterface {
private String message;
public Hello(String msg) throws RemoteException {
message = msg; }
public String say() throws RemoteException {
return message;
}
}
On peut compiler ces deux sources JAVA:
javac HelloInterface.java
javac Hello.java
ce qui crée HelloInterface.class et Hello.class.
Il faut maintenant créer les ``stubs'' et les ``squelettes''. Le rôle des stubs et des squelettes est
le suivant. Le fournisseur de service exporte un type de référence. Lorsque le client reçoit cette référence,
RMI charge un stub qui transcrit les appels à cette référence en un appel au fournisseur.
Ce processus de marshalling utilise la serialization (séquentialisation) des objets.
Du côté du serveur, un squelette effectue l'unmarshalling et invoque la méthode adéquate du serveur.
La création des stubs et squelette se fait
par la commande rmic sur le code de l'objet distant:
rmic Hello
Cela crée Hello_Stub.class et Hello_Skel.class.
Passons maintenant au client:
import java.rmi.*;
public class HelloClient {
public static void main(String[] argv) {
try {
HelloInterface hello =
(HelloInterface) Naming.lookup
("//cher.polytechnique.fr/Hello");
System.out.println(hello.say());
} catch(Exception e) {
System.out.println("HelloClient exception: "+e);
}
}
}
Ici on a supposé que le serveur - c'est-à-dire la classe sur laquelle seront repercutées
les demandes d'un client -
sera toujours sur cher. On verra dans d'autres exemples, des méthodes
plus souples.
Enfin, le serveur lui-même est la classe HelloServer suivante:
import java.rmi.*;
public class HelloServer {
public static void main(String[] argv) {
try {
Naming.rebind("Hello",new Hello("Hello, world!"));
System.out.println("Hello Server is ready.");
} catch(Exception e) {
System.out.println("Hello Server failed: "+e);
}
}
}
On peut maintenant compiler et démarrer le serveur
en faisant bien
attention au CLASSPATH (qui doit au moins contenir . et/ou les répertoires contenant
les .class nécessaires, accessibles de toutes les machines sous NFS).
javac HelloClient.java
javac HelloServer.java
Pour exécuter les programmes client et serveur, il faut démarrer le registre
(ou serveur) de noms:
rmiregistry &
ou éventuellement, rmiregistry port
& où port
est un numéro de port sur lequel le démon
rmiregistry va communiquer. Ce numéro est par défaut 1099, mais quand plusieurs utilisateurs utilisent la
même machine, il faut que plusieurs démons cohabitent sur la même machine, mais communiquent sur des ports distinct.
On peut maintenant démarrer le serveur (Hello):
[goubaul1@cher HelloNormal]$ java HelloServer
Hello Server is ready.
Enfin, on démarre des clients et on lance une exécution:
[goubaul1@loire HelloNormal]$ java HelloClient
Hello, world!
9.3 RMI avec Callback
L'idée vient de la programmation ``événementielle'', typique d'interfaces graphiques, par exemple
AWT, que vous avez vu en cours de tronc-commun.
Les ``clients'' vont s'enregistrer auprès d'un serveur.
Le ``serveur'' va les ``rappeler'' uniquement lorsque certains événements se produisent.
Le client n'a pas ainsi à faire de ``l'active polling'' (c'est-à-dire à demander des
nouvelles continuellement au serveur) pour être mis au courant des événements.
Le problème est, comment notifier un objet (distant) de l'apparition d'un événement?
Il suffit en fait de passer la référence de l'objet à rappeler au serveur chargé de suivre les
événements.
A l'apparition de l'événement, le serveur va invoquer la méthode de notification du client.
Ainsi,
pour chaque type d'événement, on crée une interface spécifique (pour le client qui veut en
être notifié),
et les clients potentiels à notifier doivent s'enregistrer auprès d'une implémentation de cette
interface.
Cela implique que ``clients'' et ``serveurs'' sont tous à leur tour ``serveurs'' et ``clients''.
Voici un petit exemple, tiré de [RR], dont les classes et interfaces sont résumées à la
figure 9.2.
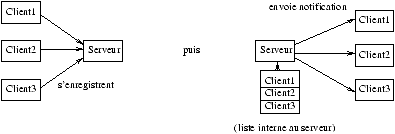
Figure 9.2: Organisation des classes, pour un RMI avec callback
On définit l'interface associée à un événement particulier, ici un
changement de température:
interface TemperatureListener extends java.rmi.Remote {
public void temperatureChanged(double temperature)
throws java.rmi.RemoteException;
}
C'est la méthode de notification de tout client intéressé par cet événement. C'est
forcément un
objet Remote.
L'interface du serveur d'événements
doit au moins pouvoir permettre l'inscription et la désinscription de clients voulant être notifiés:
interface TemperatureSensor extends java.rmi.Remote {
public double getTemperature() throws
java.rmi.RemoteException;
public void addTemperatureListener
(TemperatureListener listener)
throws java.rmi.RemoteException;
public void removeTemperatureListener
(TemperatureListener listener)
throws java.rmi.RemoteException; }
Le serveur
doit être une sous-classe de UnicastRemoteObject (pour être un serveur),
doit implémenter l'interface TemperatureListener pour pouvoir rappeler les clients en
attente,
ainsi que Runnable ici pour pouvoir avoir un thread indépendant
qui simule les changements de température.
En voici l'implémentation:
import java.util.*;
import java.rmi.*;
import java.rmi.server.*;
public class TemperatureSensorServer
extends UnicastRemoteObject
implements TemperatureSensor, Runnable {
private volatile double temp;
private Vector list = new Vector();
Le vecteur list contiendra la liste des clients.
On peut maintenant écrire le constructeur (qui prend une température initiale)
et une méthode de récupération de la température:
public TemperatureSensorServer()
throws java.rmi.RemoteException {
temp = 98.0; }
public double getTemperature()
throws java.rmi.RemoteException {
return temp; }
On a aussi des méthodes d'ajout et de retrait de clients:
public void addTemperatureListener
(TemperatureListener listener)
throws java.rmi.RemoteException {
System.out.println("adding listener -"+listener);
list.add(listener); }
public void removeTemperatureListener
(TemperatureListener listener)
throws java.rmi.RemoteException {
System.out.println("removing listener -"+listener);
list.remove(listener); }
On construit également un thread responsable du changement aléatoire de la température:
public void run()
{ Random r = new Random();
for (;;)
{ try {
int duration = r.nextInt() % 10000 +2000;
if (duration < 0) duration = duration*(-1);
Thread.sleep(duration); }
catch(InterruptedException ie) {}
int num = r.nextInt();
if (num < 0)
temp += .5;
else
temp -= .5;
notifyListeners(); } }
notifyListeners() est la méthode suivante, chargée de diffuser le changement d'événements
à tous les clients enregistrés:
private void notifyListeners() {
for (Enumeration e = list.elements(); e.hasMoreElements();)
{ TemperatureListener listener =
(TemperatureListener) e.nextElement();
try {
listener.temperatureChanged(temp);
} catch(RemoteException re) {
System.out.println("removing listener -"+listener);
list.remove(listener); } } }
on fait simplement appel, pour chaque client, à la méthode de notification
temperatureChanged.
Enfin, on enregistre le service auprès du rmiregistry (éventuellement fourni à la ligne de commande, contrairement au premier exemple de RMI simple):
public static void main(String args[]) {
System.out.println("Loading temperature service");
try {
TemperatureSensorServer sensor =
new TemperatureSensorServer();
String registry = "localhost";
if (args.length >= 1)
registry = args[0];
String registration = "rmi://"+registry+
"/TemperatureSensor";
Naming.rebind(registration,sensor);
et on démarre le thread
en charge de changer aléatoirement la température, et de gérer des exceptions:
Thread thread = new Thread(sensor);
thread.start(); }
catch (RemoteException re) {
System.err.println("Remote Error - "+re); }
catch (Exception e) {
System.err.println("Error - "+e); } } }
Passons maintenant aux clients:
import java.rmi.*;
import java.rmi.server.*;
public class TemperatureMonitor extends UnicastRemoteObject
implements TemperatureListener {
public TemperatureMonitor() throws RemoteException {}
Il étend UnicastRemoteObject car c'est un serveur également!
De même, il implémente
TemperatureListener. On remarquera qu'on a un
constructeur vide: c'est celui d'Object qui est appelé.
Maintenant, on effectue la recherche du service serveur d'événements:
public static void main(String args[]) {
System.out.println("Looking for temperature sensor");
try {
String registry = "localhost";
if (args.length >= 1)
registry = args[0];
String registration = "rmi://"+registry+
"/TemperatureSensor";
Remote remoteService = Naming.lookup(registration);
TemperatureSensor sensor = (TemperatureSensor)
remoteService;
Et on crée un moniteur que l'on enregistre auprès du serveur d'événements:
double reading = sensor.getTemperature();
System.out.println("Original temp : "+reading);
TemperatureMonitor monitor = new TemperatureMonitor();
sensor.addTemperatureListener(monitor);
On n'oublie pas de gérer les différentes exceptions possibles:
} catch(NotBoundException nbe) {
System.out.println("No sensors available"); }
catch (RemoteException re) {
System.out.println("RMI Error - "+re); }
catch (Exception e) {
System.out.println("Error - "+e); } }
Enfin, on implémente la méthode de rappel:
public void temperatureChanged(double temperature)
throws java.rmi.RemoteException {
System.out.println("Temperature change event : "
+temperature);
}
On peut maintenant compiler le tout:
[goubaul1@cher Ex3]$ javac *.java
[goubaul1@cher Ex3]$ rmic TemperatureMonitor
[goubaul1@cher Ex3]$ rmic TemperatureSensorServer
Puis exécuter le programme distribué:
[goubaul1@cher Ex3]$ rmiregistry &
[goubaul1@cher Ex3]$ java TemperatureSensorServer
Loading temperature service
On crée un premier client (sur loire):
[goubaul1@loire Ex3]$ rmiregistry &
[goubaul1@loire Ex3]$ java TemperatureMonitor cher
Looking for temperature sensor
Original temp : 100.0
Temperature change event : 99.5
Temperature change event : 100.0
Temperature change event : 100.5
Temperature change event : 100.0
Temperature change event : 100.5
Temperature change event : 101.0
Temperature change event : 100.5
Temperature change event : 100.0
Temperature change event : 100.5
Temperature change event : 101.0
Temperature change event : 101.5
On voit alors sur la console de cher:
adding listener -TemperatureMonitor_Stub[RemoteStub
[ref: [endpoint:[129.104.254.64:3224](remote),
objID:[6e1408:f29e197d47:-8000, 0]]]]
Rajoutons un moniteur sur doubs:
[goubaul1@doubs Ex3]$ rmiregistry &
[goubaul1@doubs Ex3]$ java TemperatureMonitor cher
Looking for temperature sensor
Original temp : 101.5
Temperature change event : 102.0
Temperature change event : 102.5
Temperature change event : 103.0
Temperature change event : 102.5
Temperature change event : 103.0
Temperature change event : 103.5
Temperature change event : 102.5
Temperature change event : 102.0
Ce qui produit sur cher:
adding listener -TemperatureMonitor_Stub[RemoteStub
[ref: [endpoint:[129.104.254.57:3648](remote),
objID:[6e1408:f29de7882e:-8000, 0]]]]
On voit bien que les températures et événements sont synchronisés avec l'autre client
sur loire:
Temperature change event : 102.0
Temperature change event : 102.5
Temperature change event : 103.0
Temperature change event : 102.5
Temperature change event : 103.0
Temperature change event : 103.5
^C
[goubaul1@loire Ex3]$
On a interrompu le moniteur sur loire, du coup, on voit à la console, sur cher:
removing listener -TemperatureMonitor_Stub[RemoteStub
[ref: [endpoint:[129.104.254.64:3224](remote),
objID:[6e1408:f29e197d47:-8000, 0]]]]
On interrompt par Control-C sur doubs, et on voit sur cher:
removing listener -TemperatureMonitor_Stub[RemoteStub
[ref: [endpoint:[129.104.254.57:3648](remote),
objID:[6e1408:f29de7882e:-8000, 0]]]]
9.4 RMI avec réveil de serveur
Il reste des problèmes avec les méthodes précédentes.
Même si les services sont peu souvent utilisés, il faut que les
serveurs tournent en permanence.
De plus les serveurs doivent créer et exporter les objets distants. Tout cela
représente une consommation inutile de mémoire et de CPU.
Depuis JAVA 2 on peut activer à distance un objet distant.
Cela
permet d'enregistrer un service RMI sans l'instancier,
le service RMI défini par cette méthode étant inactif
jusqu'à ce qu'un client y fasse appel, et ``réveille'' ainsi le
serveur.
Un processus démon est chargé d'écouter les requêtes et
de réveiller les services: rmid.
A la place du service, une sorte de ``proxy'' est enregistré
auprès du serveur de services RMI (rmiregistry).
Contrairement aux serveurs instances de UnicastRemoteObject,
cette ``fausse'' référence ne s'exécute que pendant un cours instant,
pour inscrire le service auprès du rmiregistry, puis
aux moments des appels au service.
Quand le client appelle ce service, le rmiregistry
fait appel à cette fausse référence.
Celle-ci vérifie si elle a un pointeur sur le vrai service.
Au cas où elle n'en a pas,
elle fait appel au démon rmid pour créer une
instance du service (cela prend un certain temps, la première fois),
puis transmet l'appel au service nouvellement créé.
En pratique
cela est transparent pour le client:
le client n'a en rien besoin de savoir comment le service est
implémenté (activation à distance, ou comme serveur
permanent).
La création du service est un peu différente du cas
du serveur résident, mais son code reste similaire.
Les différentes classes et interfaces sont représentées à la figure
9.3.
Celles-ci font appel aux paquetages RMI suivants:
-
java.rmi définit l'interface RemoteInterface,
et les exceptions,
- java.rmi.activation (depuis JAVA2): permet l'activation
à distance des objets,
- java.rmi.dgc: s'occupe du ramassage de miettes dans
un environnement distribué,
- java.rmi.registry fournit l'interface permettant de
représenter un
rmiregistry, d'en créer un, ou d'en
trouver un,
- java.rmi.server fournit les classes et interfaces pour
les serveurs RMI.
On pourra se reporter à la documentation en ligne:
http://java.sun.com/j2se/1.4.2/docs/guide/rmi/index.html
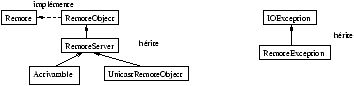
Figure 9.3: Les différentes classes et interfaces RMI
Commençons par examiner la façon dont on peut définir
l'interface du serveur
activable à distance.
L'interface du service ne contient que les méthodes désirées
sans argument, mais devant renvoyer une exception de type
java.rmi.RemoteException. Ceci est imposé par rmic:
public interface InterfaceObjetActivable
extends java.rmi.Remote
{ public void MethodeA() throws java.rmi.RemoteException;
public void MethodeB() throws java.rmi.RemoteException;
... }
Cette interface peut être en fait implémentée par un objet activable
à distance ou un service permanent UnicastRemoteObject.
L'implémentation
du serveur
doit être une instance de
java.rmi.activation.Activatable,
(en fait, il y a aussi moyen de faire autrement)
et doit implémenter un constructeur particulier,
ainsi que les méthodes désirées MethodeA etc.
On aura typiquement:
public class ImplementationObjetActivable extends
java.rmi.activation.Activatable
implements InterfaceObjetActivable
{
public ImplementationObjetActivable (
java.rmi.activation.ActivationID activationID,
java.rmi.MashalledObject data) throws
java.rmi.RemoteException
{ super(activationID,0); }
(appelle le constructeur de la classe parent Activatable(ID,0))
Enfin, il faudra implémenter la méthode rendant le service attendu:
public void doSomething()
{
...
}
}
L'activation de l'objet
est
en général incluse dans le main de l'implémentation
de l'objet (service). Le
code est assez compliqué du fait que doivent être gérés
la politique de sécurité,
les propriétés et droits du code exécutable,
et enfin l'inscription auprès de rmid et rmiregistry.
9.4.1 Exemple d'une ``lampe''
On va construire les classes représentées à la figure 9.4.
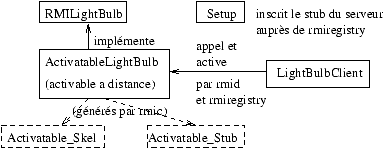
Figure 9.4: Classes pour la lampe activable à distance
L'interface du serveur activable est:
package examples;
import java.rmi.*;
public interface RMILightBulb extends Remote {
public void on() throws RemoteException;
public void off() throws RemoteException;
public boolean isOn() throws RemoteException;
}
Et un client possible est décrit plus bas.
Remarquez
qu'il serait le même si on avait utilisé une implémentation
du serveur comme instance de UnicastRemoteObject.
package examples;
import java.rmi.*;
public class LightBulbClient {
public static void main(String args[]) {
System.out.println("Recherche d'une lampe...");
A ce point du code, on doit utiliser rmiregistry:
/* voir Server */
System.setSecurityManager(new RMISecurityManager());
try {
String registry = "localhost";
if (args.length >= 1)
registry = args[0];
String registration = "rmi://"+registry+
"/ActivatableLightBulbServer";
Remote remoteService = Naming.lookup(registration);
RMILightBulb bulbService = (RMILightBulb) remoteService;
Cela permet de spécifier la machine où se trouve le serveur, et le rmiregistry correspondant.
Maintenant on procède à l'appel aux services:
System.out.println("Appel de bulbservice.on()");
bulbService.on();
System.out.println("Lampe : "+bulbService.isOn());
System.out.println("Appel de bulbservice.off()");
bulbService.off();
System.out.println("Lampe : "+bulbService.isOn());
Enfin on doit récuper les exceptions:
} catch(NotBoundException nbe) {
System.out.println("Pas de lampe dans le
repertoire de services!");
} catch(RemoteException re) {
System.out.println("RMI Error - "+re);
} catch(Exception e) {
System.out.println("Error - "+e);
}
}
}
Le serveur activable à distance est maintenant:
package examples;
import java.rmi.*;
import java.rmi.activation.*;
public class ActivatableLightBulbServer
extends Activatable implements RMILightBulb {
public ActivatableLightBulbServer
(ActivationID activationID,
MarshalledObject data)
throws RemoteException {
super(activationID,0);
setBulb(false); }
On arrive enfin aux services eux-mêmes:
public boolean isOn() throws RemoteException {
return getBulb();
}
public void setBulb(boolean value)
throws RemoteException {
lightOn = value; }
public boolean getBulb() throws RemoteException {
return lightOn; } }
private boolean lightOn;
public void on() throws RemoteException {
setBulb(true);
}
public void off() throws RemoteException {
setBulb(false);
}
On en arrive au main de Setup et à la gestion de la
politique de sécurité:
package examples;
import java.rmi.*;
import java.rmi.activation.*;
import java.util.Properties;
public class Setup {
public static void main(String[] args) throws Exception {
System.setSecurityManager(new RMISecurityManager());
Properties props = new Properties();
props.put("java.security.policy",
"/users/profs/info/goubaul1/Cours03/RMI/Ex2/activepolicy");
La politique de sécurité doit être spécifiée à la ligne
de commande; on le verra plus loin quand on parle de l'exécution.
On doit également créer un descripteur de groupe:
ActivationGroupDesc.CommandEnvironment ace = null;
ActivationGroupDesc exampleGroup =
new ActivationGroupDesc(props, ace);
qui
permet d'associer des propriétés et des droits à l'exécution.
On récupére le descripteur du démon rmid, puis
on y enregistre le descripteur de groupe:
ActivationGroupID agi =
ActivationGroup.getSystem().registerGroup(exampleGroup);
On crée maintenant un descripteur d'activation du code.
Au sein du groupe nouvellement créé,
on passe le nom de la classe, l'endroit où se trouve le code, et une
donnée optionnelle, une version ``serialized'' de l'objet
distant (de type MarshalledObject):
String location =
"file:/users/profs/info/goubaul1/Cours03/RMI/Ex2/";
MarshalledObject data = null;
ActivationDesc desc = new ActivationDesc
(agi, "examples.ActivatableLightBulbServer",
location, data);
Revenons au code.
On indique l'endroit où se trouve le
code exécutable:
java.io.File location = new java.io.File(".");
String strLoc = "file://"
+URLEncoder.encode(location.getAbsolutePath(),"UTF-8");
System.out.println("Code \`a ex\'ecuter : "+strLoc);
L'encodage URLEncoder permet d'être compatible avec
les systèmes Windows etc. On peut aussi utiliser un serveur
http://... pour le chargement dynamique de classes.
Sur un petit système en effet, on peut gérer les stubs créés: il suffit en effet
de recopier, ou d'avoir accès par NFS à tous ces fichiers
sur toutes les machines considérées. Mais ce n'est pas pratique
tout le temps, car cela limite singulièrement la distance entre le client
et le serveur. En fait, on
peut acccéder aux serveurs par adresse http:
java -Djava.rmi.server.codebase=http://hostname:port/path
On enregistre maintenant l'objet auprès du rmid:
RMILightBulb stub = (RMILightBulb)Activatable.register(desc);
System.out.println("Got stub for ActivatableLightBulbServer");
Cela
renvoie un ``stub'' que l'on peut enregistrer auprès du serveur
de services rmiregistry:
Naming.rebind("ActivatableLightBulbServer", mri);
System.out.println("Exported ActivatableLightBulbServer");
System.exit(0); } }
Cela est
similaire au cas d'implémentation par UnicastRemoteObject -
sauf que c'est le ``stub'' et pas l'objet lui-même qui est inscrit.
9.4.2 Complément: politiques de sécurité
Un programme JAVA peut dans certaines circonstances avoir à s'associer une ``politique de
sécurité'' donnant les droits d'objets provenant de certaines autres machines.
C'est typiquement le cas pour des objets Serializable transitant entre applications distantes.
Par
exemple, la connection par socket à une machine distante passe par la méthode
checkConnect(String host, int port) du SecurityManager courant
(en fait, c'est une sous-classe RMISecurityManager pour les politiques concernant RMI),
définissant la politique
de sécurité courante. En cas de non autorisation, on obtient des messages du type:
java.security.AccessControlException: access denied
(java.net.SocketPermission 127.0.0.1:1099 connect,resolve)
Pour associer une politique de sécurité à un code JAVA, il faut
construire un objet instance de SecurityManager,
surcharger les fonctions check... dont on veut changer la politique de sécurité,
et invoquer la méthode de la classe System, setSecurityManager, en lui passant
cet objet créé plus haut.
On fera par exemple:
System.setSecurityManager(new RMISecurityManager() {
public void checkConnect(String host, int port) {}
public void checkConnect(String host, int port,
Object context) {}
});
Ce code
utilise une classe anonyme, sous-classe de RMISecurityManager
dans laquelle les méthodes
checkConnect retournent faux. On n'a donc
aucune permission de créer des sockets pour communiquer avec
d'autres machines.
A partir de JAVA 1.2, une autre méthode est fournie en plus.
Toutes les méthodes check... font appel à la méthode checkPermission
à laquelle on passe le type de permission souhaité.
Par exemple checkConnect appelle checkPermission sur un objet SocketPermission.
La liste des permissions autorisées est gérée par la classe Permissions.
Chaque programme a une politique de sécurité courante, instance de Policy,
qui est Policy.get Policy().
On peut modifier la politique de sécurité courante (comme avant avec le
SecurityManager) en faisant appel à Policy.setPolicy.
Un fichier de permissions (lu au démarrage d'un programme) de la forme:
grant codeBase "file:/home/goubault/-" {
permission java.security.AllPermission;
};
donnera tous les droits à tous les programmes dans /home/goubault/
Un autre exemple un peu plus fin serait:
grant codeBase "file:/home/goubault/-" {
permission java.net.SocketPermission
"129.104.254.54:1024-", "connect, accept";
}
qui permet d'utiliser les sockets sur loire.polytechnique.fr, avec un numéro de
port supérieur à 1024.
On peut aussi utiliser policytool pour générer ces fichiers. En pratique,
pour utiliser le fichier de permissions en question (fichier), à l'exécution du main
de la classe maclasse, tout en spécifiant le répertoire contenant le code, on fera:
java -Djava.security.policy=FICHIER
-D-Djava.rmi.server.codebase=file:/LOCATION
MACLASSE
Revenons maintenant à l'exemple de la section précédente.
Il faut le compiler, et créer les fichiers stubs et squelettes:
javac -d . RMILightBulb.java
javac -d . LightBulbClient.java
javac -d . Setup.java
javac -d . ActivatableLightBulbServer.java
rmic ActivatableLightBulbServer
(le -d . pour créer les répertoires correspondants aux packages)
On lance maintenant les démons
sur la machine correspondant au serveur (ici loire). On commence par
lancer rmiregistry (avec un CLASSPATH ne contenant pas les .class appelés par
le client)
puis par spécifier la politique de sécurité. Par exemple ici, on donne toutes
les permissions (dans le fichier activepolicy):
grant {
permission java.security.AllPermission;
};
Enfin on lance rmid -J-Djava.security.policy=activepolicy
Exécutons enfin ce programme:
[goubaul1@loire Ex2]$ java
-Djava.security.policy=activepolicy
-Djava.rmi.server.codebase=file:/. examples.Setup
Got the stub for the ActivatableLightBulbServer
Exported ActivatableLightBulbServer
(pour spécifier la politique de sécurité)
On exécute le client
sur cher:
[goubaul1@cher Ex2]$ java -Djava.security.policy=activepolicy
examples.LightBulbClient loire
Looking for light bulb service
Invoking bulbservice.on()
Bulb state : true
Invoking bulbservice.off()
Bulb state : false
Compararons brièvement avec une implémentation de type
UnicastRemoteObject
Le serveur lui-même (voir ~goubaul1/RMI/Ex1) est:
public class RMILightBulbImpl extends
java.rmi.server.UnicastRemoteObject
implements RMILightBulb {
public RMILightBulbImpl()
throws java.rmi.RemoteException {
setBulb(false);
}
private boolean lightOn;
public void on()
throws java.rmi.RemoteException {
setBulb(true); }
public void off()
throws java.rmi.RemoteException {
setBulb(false); }
public boolean isOn()
throws java.rmi.RemoteException {
return getBulb(); }
public void setBulb(boolean value) {
lightOn = value; }
public boolean getBulb() {
return lightOn; } }
Mais, l'interface du serveur reste la même:
public interface RMILightBulb extends java.rmi.Remote {
public void on() throws java.rmi.RemoteException;
public void off() throws java.rmi.RemoteException;
public boolean isOn() throws java.rmi.RemoteException;
}
Et on a exactement le même client.
L'exécution se ferait de la façon suivante:
sur cher (serveur):
[goubaul1@cher Ex1]$ java LightBulbServer
Loading RMI service
RemoteStub [ref: [endpoint:[129.104.254.54:1867](local),
objID:[0]]]
Et sur loire (client):
[goubaul1@loire Ex1]$ java LightBulbClient cher
Looking for light bulb service
Invoking bulbservice.on()
Bulb state : true
Invoking bulbservice.off()
Bulb state : false
Corba est une architecture distribuée dans laquelle des clients
émettent des requêtes à destination d'objets, qui s'exécutent dans des
processus serveurs. Ces objets répondent aux clients par la
transmission d'informations bien que ces deux éléments (client et
serveur) soient localisés dans des espaces mémoire différents,
généralement sur des machines distantes.
Lors du développement d'une application Corba, le dialogue entre les
différents constituants est rendu totalement transparent pour le
développeur. Le serveur déclare mettre à disposition ses objets et le
client se contente de demander une connexion à un ou à certains de ces
objets, sans pour autant en connaître obligatoirement la localisation
ou le format. Dans ces deux cas, l'ORB (Object Request Broker) se
charge de localiser les objets, de les charger en mémoire et de
transmettre au serveur les demandes du client (voir la Figure
9.5). Il assure ensuite des
opérations de gestion ou de maintenance, comme la
gestion des erreurs ou leur destruction. Dans cette architecture,
l'application
cliente ne se préoccupe pas des détails d'implémentation des objets
serveurs, elle se contente de s'y connecter et de les utiliser.
L'ORB prend en charge la communication entre les différents composants
du système distribué.
Le dialogue Corba, entre le client, le serveur et l'ORB est décrit à la figure
9.5.
Le cycle de développement CORBA est représenté à la figure
9.6.
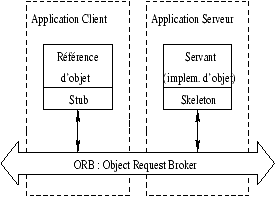
Figure 9.5: Le dialogue CORBA
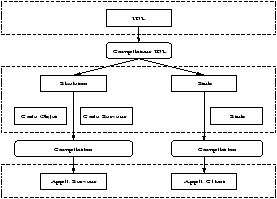
Figure 9.6: Le cycle de développement CORBA
On commence par
écrire l'interface de l'objet en IDL. C'est-à-dire que l'on
définit dans
le langage de description d'interfaces Corba (``Interface Definition Language'')
des opérations disponibles sur l'objet.
Ensuite, on
compile l'IDL. Cela engendre des modules stub (pour le client)
et skeleton (pour le serveur).
Ces modules gèrent l'invocation des méthodes distantes.
Enfin, on implémente l'objet. On dérive une classe à partir du squelette
généré à l'étape précédente. Les données et méthodes de cette classe doivent
correspondre à celles qui sont décrites dans l'IDL. Lors de l'appel des
méthodes sur l'objet, le code défini sera exécuté par l'application serveur.
Ensuite, on
rédige l'application serveur : ce code sert à initialiser l'objet
et à le mettre à disposition des différentes applications clientes.
On compile le serveur. Cela génère l'exécutable de l'application serveur.
On réalise l'application cliente : cette application se connecte à l'objet
distant pour lui demander d'exécuter des méthodes. Elle traite ensuite les
données transmises par le serveur à l'issue de l'exécution des traitements distants.
Enfin, on compile le client. Cela génère l'exécutable de l'application client.
Donnons un exemple de l'écriture de l'interface de l'objet en IDL:
interface Vecteur {
typedef double vect[100]; // Definition du type vect
attribute long size; // size est un attribut
// de type long (entier)
attribute vect T ; // T est un attribut de
// type vect
double maxElement(); // maxElement est une
// methode retournant un double
void mult(in double a); // mult est une methode
// prenant pour parametre
// un double transmis
}; //par le client (mot cle in)
Comme on le voit dans cet exemple, les
principaux types définis par le langage IDL sont short et
long pour les entiers, float et double pour
les flottants, char et string pour les caractères.
Les
types composés sont les tableaux ainsi que d'autres structures
à l'aide des mots clés enum, struct ou union, etc.
Le mot clé attribute appartient au langage IDL, tout comme in
qui indique le sens de passage du paramètre (du client vers le serveur).
Symétriquement le type de passage des paramètres out
permet de réaliser un passage par adresse: par exemple
void maxElement(out double m); Le type inout
peut être utilisé pour les paramètres devant être lus et écrits.
On compile l'interface IDL par la commande idlj -fall Vecteur.idl.
Les principaux fichiers qui sont générés sont les suivants :
-
VecteurOperations.java : définition de l'interface qui contient
la signature des méthodes de l'objet Vecteur.
- Vecteur.java : définition de l'interface Vecteur qui
hérite de VecteurOperations.
- VecteurHelper.java : regroupe des méthodes destinées à vous
aider lors de l'utilisation des objets Vecteur.
- VecteurHolder.java : outils pour prendre en charge le passage
de paramètres avec les méthodes de l'objet Vecteur.
- _VecteurStub.java : stub de l'objet Vecteur.
Cette classe sera utilisée dans le code de notre client de façon
implicite, elle représentera l'objet distant en mettant à notre
disposition les méthodes qui s'y trouvent.
- _VecteurImplBase.java : squelette de l'objet Vecteur.
C'est la classe de base de notre futur objet vecteur. On en dérivera
une classe pour coder le fonctionnement réel de notre objet.
L'implémentation de l'objet se fait en
créant la classe de l'objet que nous souhaitons mettre à disposition: pour cela, on utilise le squelette
généré précédemment.
la classe VecteurImplem que nous allons créer étendra la classe _VecteurImplBase
produite par le compilateur IDL
et implémentera les méthodes définies par l'interface
VecteurOperations.java:
public class VecteurImplem extends _VecteurImplBase {
private int size=100;
private double T[];
VecteurImplem(double[] Tab) {
for(int i=0;i<size;i++) {
T[i]=Tab[i]; } }
VecteurImplem() {} ;
public int size() {
return size; }
public void size(int newSize) {
size = newSize; }
public double[] T() {
return T; }
public void T(double[] newT) {
for(int i=0;i<size;i++) {
T[i]=newT[i]; } }
public double maxElement () {
double m = T[0];
for (int i=1;i<size;i++) {
if (T[i]>m) { m = T[i]; } };
return m; }
public void mult(double a) {
for (int i=0;i<size;i++) {
T[i]=T[i]*a; } } }
La classe implémentant l'objet qui nous intéresse
doit implémenter toutes les méthodes définies
par l'interface VecteurOperations.
On doit donc déclarer en particulier
les attributs définis dans l'interface IDL.
Il faut naturellement définir
les méthodes de création des objets de la classe.
La méthode maxElement
devra retourner l'élément maximal du vecteur et la méthode mult
devra multiplier tous
les éléments du vecteur par la valeur du paramètre.
Pour le serveur CORBA,
nous allons créer une application
hôte, qui contiendra l'objet Vecteur:
import org.omg.CosNaming.*;
import org.omg.CosNaming.NamingContextPackage.*;
import org.omg.CORBA.*;
public class VecteurServeur {
public static void main(String args[]) {
try{
// Cree et initialise l'ORB
ORB orb = ORB.init(args, null);
// Cree le servant et l'enregistre sur l'ORB
VecteurImplem vecteurRef = new VecteurImplem();
orb.connect(vecteurRef);
// Obtention de la reference du RootPOA
org.omg.CORBA.Object objRef =
orb.resolve_initial_references("NameService");
NamingContext ncRef = NamingContextHelper.narrow(objRef);
// Enregistre la reference de l'objet
NameComponent nc = new NameComponent("Vecteur", "");
NameComponent path[] = {nc};
ncRef.rebind(path, vecteurRef);
// attend les invocations de clients
java.lang.Object sync = new java.lang.Object();
synchronized (sync) {
sync.wait(); }
} catch (Exception e) {
System.err.println("ERROR: " + e);
e.printStackTrace(System.out); } } }
Les principales actions réalisées par le serveur sont,
la création d'une instance de l'ORB,
d'une instance du servant (l'implémentation d'un objet Vecteur) et
son enregistrement sur l'ORB.
On obtient ainsi une référence à un objet CORBA pour le nommage et pour y enregistrer
le nouvel objet sous le nom ``Vecteur''.
Le serveur attend ensuite l'invocation de méthodes de l'objet.
On pourra se reporter à
http://java.sun.com/j2se/1.4.2/docs/guide/corba/index.html
pour plus de détails.
On a maintenant une application autonome qui, lors de son lancement, crée un
objet Vecteur et le met à disposition des autres applications.
Tout comme le
serveur, le client devra initialiser l'ORB. Il pourra ensuite se connecter
à l'objet et l'utiliser:
import org.omg.CosNaming.*;
import org.omg.CORBA.*;
public class VecteurClient {
public static void main(String args[]) {
try{
// Cree et initialise l'ORB.
ORB orb = ORB.init(args, null);
// Obtention de la reference du RootPOA
org.omg.CORBA.Object objRef =
orb.resolve_initial_references("NameService");
NamingContext ncRef = NamingContextHelper.narrow(objRef);
// trouve la r\'ef\'erence \`a l'objet
NameComponent nc = new NameComponent("Vecteur", "");
NameComponent path[] = {nc};
Vecteur vecteurRef = VecteurHelper.narrow
(ncRef.resolve(path));
// Utilisation de l'objet
...
} catch (Exception e) {
System.out.println("ERROR : " + e) ;
e.printStackTrace(System.out); } } }
Le client initialise ainsi l'ORB et obtient une référence au contexte de nommage.
Il y recherche ensuite ``Vecteur'' et reçoit une référence de cet objet Corba.
Il peut ensuite invoquer les méthodes de l'objet.
Pour plus de détails, on pourra se reporter à
http://java.sun.com/products/jdk/1.2/docs/guide/
idl/tutorial/GSapp.html.
Maintenant on compile toutes les applications ainsi écrites:
javac *.java
Pour l'exécution,
on procéde dans l'ordre suivant.
On commence par initialiser le serveur de noms:
tnameserv -ORBInitialPort 1050
1050 est le port utilisé par le serveur. Sous Solaris par exemple, il faut être root pour
utiliser un port inférieur à 1024.
Ensuite on initialise le serveur par
java VecteurServer -ORBInitialHost namerserverhost -ORBInitialPort 1050
nameserverhost est le nom de la machine sur laquelle s'exécute le
serveur de noms.
Enfin, on exécute le client par:
java VecteurClient -ORBInitialHost namerserverhost -ORBInitialPort 1050
Dans ce chapitre nous allons décrire quelques façons classiques de paralléliser certains calculs d'algèbre
linéaire. Ceux-ci ont été particulièrement étudiés car de très nombreux codes scientifiques, requiérant une grande puissance de calcul, utilisent
des calculs matriciels, de façon intensive.
10.1 Produit matrice-vecteur sur anneau
On cherche à calculer y=Ax, où
A est une matrice de dimension n × n,
x est un vecteur à n composantes (de 0 à n-1), le tout
sur un anneau de p processeurs, avec r=n/p entier.
Le programme séquentiel est simple.
En effet, le calcul du produit matrice-vecteur revient au calcul de n produits scalaires:
for (i=1;i<=n;i++)
for (j=1;j<=n;j++)
y[i] = y[i]+a[i,j]*x[j];
On essaie donc de
distribuer le calcul des produits scalaires aux différents processeurs.
Chaque processeur a en mémoire r lignes de la matrice A rangées dans une matrice
a de dimension r × n.
Le processeur Pq contient
les lignes qr à (q+1)r-1 de la matrice A et les composantes de même
rang des vecteurs x et y:
float a[r][n];
float x[r],y[r];
Le programme distribué correspondant à la parallélisation de cet algorithme
séquentiel est:
matrice-vecteur(A,x,y) {
q = my_num();
p = tot_proc_num();
for (step=0;step<p;step++) {
send(x,r);
for (i=0;i<r;i++)
for (j=0;j<r;j++)
y[i] = y[i]+a[i,(q-step mod p)r+j]*x[j];
receive(temp,r);
x = temp;
}
}
Donnons un exemple des différentes étapes (boucle extérieure, sur step), pour n=8.
La distribution initiale des données est donc comme suit:
| P0 |
æ
è |
| A00 |
A01 |
A02 |
A03 |
A04 |
A05 |
A06 |
A07 |
| A10 |
A11 |
A12 |
A13 |
A14 |
A15 |
A16 |
A17 |
|
|
ö
ø |
|
|
|
| |
| P1 |
æ
è |
| A20 |
A21 |
A22 |
A23 |
A24 |
A25 |
A26 |
A27 |
| A30 |
A31 |
A32 |
A33 |
A34 |
A35 |
A36 |
A37 |
|
|
ö
ø |
|
|
|
| |
| P2 |
æ
è |
| A40 |
A41 |
A42 |
A43 |
A44 |
A45 |
A46 |
A47 |
| A50 |
A51 |
A52 |
A53 |
A54 |
A55 |
A56 |
A57 |
|
|
ö
ø |
|
|
|
| |
| P3 |
æ
è |
| A60 |
A61 |
A62 |
A63 |
A64 |
A65 |
A66 |
A67 |
| A70 |
A71 |
A72 |
A73 |
A74 |
A75 |
A76 |
A77 |
|
|
ö
ø |
|
|
A la première étape, chacun des p=4 processeurs considère les sous-matrices
suivantes:
| P0 |
æ
è |
| A00 |
A01 |
· |
· |
· |
· |
· |
· |
| A10 |
A11 |
· |
· |
· |
· |
· |
· |
|
|
ö
ø |
|
|
temp |
¬ |
|
|
| |
| P1 |
æ
è |
| · |
· |
A22 |
A23 |
· |
· |
· |
· |
| · |
· |
A32 |
A33 |
· |
· |
· |
· |
|
|
ö
ø |
|
|
temp |
¬ |
|
|
| |
| P2 |
æ
è |
| · |
· |
· |
· |
A44 |
A45 |
· |
· |
| · |
· |
· |
· |
A54 |
A55 |
· |
· |
|
|
ö
ø |
|
|
temp |
¬ |
|
|
| |
| P3 |
æ
è |
| · |
· |
· |
· |
· |
· |
A66 |
A67 |
| · |
· |
· |
· |
· |
· |
A76 |
A77 |
|
|
ö
ø |
|
|
temp |
¬ |
|
A la deuxième étape, les processeurs ont en mémoire les sous-matrices suivantes:
| P0 |
æ
è |
| · |
· |
· |
· |
· |
· |
A06 |
A07 |
| · |
· |
· |
· |
· |
· |
A16 |
A17 |
|
|
ö
ø |
|
|
temp |
¬ |
|
|
| |
| P1 |
æ
è |
| A20 |
A21 |
· |
· |
· |
· |
· |
· |
| A30 |
A31 |
· |
· |
· |
· |
· |
· |
|
|
ö
ø |
|
|
temp |
¬ |
|
|
| |
| P2 |
æ
è |
| · |
· |
A42 |
A43 |
· |
· |
· |
· |
| · |
· |
A52 |
A53 |
· |
· |
· |
· |
|
|
ö
ø |
|
|
temp |
¬ |
|
|
| |
| P3 |
æ
è |
| · |
· |
· |
· |
A64 |
A65 |
· |
· |
| · |
· |
· |
· |
A74 |
A75 |
· |
· |
|
|
ö
ø |
|
|
temp |
¬ |
|
Puis à la troisième étape:
| P0 |
æ
è |
| · |
· |
· |
· |
A04 |
A05 |
· |
· |
| · |
· |
· |
· |
A14 |
A15 |
· |
· |
|
|
ö
ø |
|
|
temp |
¬ |
|
|
| |
| P1 |
æ
è |
| · |
· |
· |
· |
· |
· |
A26 |
A27 |
| · |
· |
· |
· |
· |
· |
A36 |
A37 |
|
|
ö
ø |
|
|
temp |
¬ |
|
|
| |
| P2 |
æ
è |
| A40 |
A41 |
· |
· |
· |
· |
· |
· |
| A50 |
A51 |
· |
· |
· |
· |
· |
· |
|
|
ö
ø |
|
|
temp |
¬ |
|
|
| |
| P3 |
æ
è |
| · |
· |
A62 |
A63 |
· |
· |
· |
· |
| · |
· |
A72 |
A73 |
· |
· |
· |
· |
|
|
ö
ø |
|
|
temp |
¬ |
|
Enfin à la quatrième étape:
| P0 |
æ
è |
| · |
· |
A02 |
A03 |
· |
· |
· |
· |
| · |
· |
A12 |
A13 |
· |
· |
· |
· |
|
|
ö
ø |
|
|
temp |
¬ |
|
|
| |
| P1 |
æ
è |
| · |
· |
· |
· |
A24 |
A25 |
· |
· |
| · |
· |
· |
· |
A34 |
A35 |
· |
· |
|
|
ö
ø |
|
|
temp |
¬ |
|
|
| |
| P2 |
æ
è |
| · |
· |
· |
· |
· |
· |
A46 |
A47 |
| · |
· |
· |
· |
· |
· |
A56 |
A57 |
|
|
ö
ø |
|
|
temp |
¬ |
|
|
| |
| P3 |
æ
è |
| A60 |
A61 |
· |
· |
· |
· |
· |
· |
| A70 |
A71 |
· |
· |
· |
· |
· |
· |
|
|
ö
ø |
|
|
temp |
¬ |
|
En notant ta le temps de calcul élémentaire,
tc le temps de communication élémentaire, on se propose d'estimer le temps de
calcul de cet algorithme, donc de mesurer ses performances.
Il y a p étapes identiques dans cet algorithme,
chacune de temps égal au temps le plus long parmi le temps de calcul local et le temps
de communication: max(r2 ta,b+rtc).
On obtient donc un temps total de p*max(r2 ta,b+rtc).
Quand n est assez grand, r2 ta devient prépondérant, d'où asympotiquement un temps
de n2/pta. C'est-à-dire que asymptotiquement, l'efficacité tend vers 1 !
Remarquez que l'on aurait
aussi pu procéder à un échange total de x au début.
10.2 Factorisation LU
On cherche maintenant à résoudre un système linéaire dense
Ax=b par triangulation de Gauss. Un programme séquentiel qui implémente cela est:
for (k=0;k<n-1;k++) {
prep(k): for (i=k+1;i<n;i++)
a[i,k]=a[i,k]/a[k,k];
for (j=k+1;j<n;j++)
update(k,j): for (i=k+1;i<n;i++)
a[i,j]=a[i,j]-a[i,k]*a[k,j];
}
On le parallélise en distribuant les colonnes aux différents processeurs.
On va supposer que cette distribution nous est donnée par une fonction alloc telle
que alloc(k)=q veut dire que la kième colonne est affectée à la mémoire locale
de Pq.
On utilisera la fonction broadcast, pour faire en sorte qu'à l'étape k, le processeur
qui possède la colonne k la diffuse à tous les autres.
On va supposer dans un premier temps que alloc(k)=k. On obtient alors:
q = my_num();
p = tot_proc_num();
for (k=0;k<n-1;k++) {
if (k == q) {
prep(k): for (i=k+1;i<n;i++)
buffer[i-k-1] = a[i,k]/a[k,k];
broadcast(k,buffer,n-k);
}
else {
receive(buffer,n-k);
update(k,q): for (i=k+1;k<n;k++)
a[i,q] = a[i,q]-buffer[i-k-1]*a[k,q]; }
}
Dans le cas plus général, il faut gérer les indices dans les blocs de colonnes.
Maintenant chaque processeur gère r=n/p colonnes, avec des indices locaux:
q = my_num();
p = tot_proc_num();
l = 0;
for (k=0;k<n-1;k++) {
if (alloc(k) == q) {
prep(k): for (i=k+1;i<n;i++)
buffer[i-k-1] = a[i,l]/a[k,l];
l++; }
broadcast(alloc(k),buffer,n-k);
for (j=l;j<r;j++)
update(k,j): for (i=k+1;k<n;k++)
a[i,j] = a[i,j]-buffer[i-k]*a[k,j]; }
Cet algorithme présente néanmoins un certain nombre de défauts.
Premièrement, le nombre de données varie au cours des étapes (il y en a de moins en moins).
Ensuite, le volume de calcul n'est pas proportionnel au volume des données: quand un processeur
a par exemple r colonnes consécutives, le dernier processeur a moins de calcul (que de données)
par rapport au premier.
Il faudrait donc trouver une fonction
d'allocation qui réussisse à équilibrer le volume des données
et du travail!
Cet équilibrage de charge doit être réalisé
à chaque étape de l'algorithme, et pas seulement de façon globale.
10.2.1 Cas de l'allocation cyclique par lignes
Pour p=4, et n=8 on a la répartition initiale des données comme suit:
æ
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
è |
| P0 |
P1 |
P2 |
P3 |
P0 |
P1 |
P2 |
P3 |
| A00 |
A01 |
A02 |
A03 |
A04 |
A05 |
A06 |
A07 |
| A10 |
A11 |
A12 |
A13 |
A14 |
A15 |
A16 |
A17 |
| A20 |
A21 |
A22 |
A23 |
A24 |
A25 |
A26 |
A27 |
| A30 |
A31 |
A32 |
A33 |
A34 |
A35 |
A36 |
A37 |
| A40 |
A41 |
A42 |
A43 |
A44 |
A45 |
A46 |
A47 |
| A50 |
A51 |
A52 |
A53 |
A54 |
A55 |
A56 |
A57 |
| A60 |
A61 |
A62 |
A63 |
A64 |
A65 |
A66 |
A67 |
| A70 |
A71 |
A72 |
A73 |
A74 |
A75 |
A76 |
A77 |
|
ö
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
ø |
A k=0:
æ
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
è |
| P0: p0; b |
P1 |
P2 |
P3 |
P0 |
P1 |
P2 |
P3 |
| U00 |
A01 |
A02 |
A03 |
A04 |
A05 |
A06 |
A07 |
| L10 |
A11 |
A12 |
A13 |
A14 |
A15 |
A16 |
A17 |
| L20 |
A21 |
A22 |
A23 |
A24 |
A25 |
A26 |
A27 |
| L30 |
A31 |
A32 |
A33 |
A34 |
A35 |
A36 |
A37 |
| L40 |
A41 |
A42 |
A43 |
A44 |
A45 |
A46 |
A47 |
| L50 |
A51 |
A52 |
A53 |
A54 |
A55 |
A56 |
A57 |
| L60 |
A61 |
A62 |
A63 |
A64 |
A65 |
A66 |
A67 |
| L70 |
A71 |
A72 |
A73 |
A74 |
A75 |
A76 |
A77 |
|
ö
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
ø |
Puis, toujours à k=0:
æ
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
è |
| P1: r;u0,1 |
P2: r; u0,2 |
P3: r; u0,3 |
P0: u0,4 |
P1 |
P2 |
P3 |
| U00 |
U01 |
U02 |
U03 |
U04 |
A05 |
A06 |
A07 |
| L10 |
A11' |
A12' |
A13' |
A14' |
A15 |
A16 |
A17 |
| L20 |
A21' |
A22' |
A23' |
A24' |
A25 |
A26 |
A27 |
| L30 |
A31' |
A32' |
A33' |
A34' |
A35 |
A36 |
A37 |
| L40 |
A41' |
A42' |
A43' |
A44' |
A45 |
A46 |
A47 |
| L50 |
A51' |
A52' |
A53' |
A54' |
A55 |
A56 |
A57 |
| L60 |
A61' |
A62' |
A63' |
A64' |
A65 |
A66 |
A67 |
| L70 |
A71' |
A72' |
A73' |
A74' |
A75 |
A76 |
A77 |
|
ö
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
ø |
Ensuite:
æ
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
è |
| P0 |
P1 |
P2 |
P3 |
P0 |
P1: r; u0,5 |
P2: r; u0,6 |
P3: r; u0,7 |
| U00 |
U01 |
U02 |
U03 |
U04 |
U05 |
U06 |
U07 |
| L10 |
A11' |
A12' |
A13' |
A14' |
A15' |
A16' |
A17' |
| L20 |
A21' |
A22' |
A23' |
A24' |
A25' |
A26' |
A27' |
| L30 |
A31' |
A32' |
A33' |
A34' |
A35' |
A36' |
A37' |
| L40 |
A41' |
A42' |
A43' |
A44' |
A45' |
A46' |
A47' |
| L50 |
A51' |
A52' |
A53' |
A54' |
A55' |
A56' |
A57' |
| L60 |
A61' |
A62' |
A63' |
A64' |
A65' |
A66' |
A67' |
| L70 |
A71' |
A72' |
A73' |
A74' |
A75' |
A76' |
A77' |
|
|
ö
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
ø |
Maintenant, quand k=1:
æ
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
è |
| P0 |
P1: p1; b |
P2 |
P3 |
P0 |
P1 |
P2 |
P3 |
| U00 |
U01 |
U02 |
U03 |
U04 |
U05 |
U06 |
U07 |
| L10 |
U11 |
A12' |
A13' |
A14' |
A15' |
A16' |
A17' |
| L20 |
L21 |
A22' |
A23' |
A24' |
A25' |
A26' |
A27' |
| L30 |
L31 |
A32' |
A33' |
A34' |
A35' |
A36' |
A37' |
| L40 |
L41 |
A42' |
A43' |
A44' |
A45' |
A46' |
A47' |
| L50 |
L51 |
A52' |
A53' |
A54' |
A55' |
A56' |
A57' |
| L60 |
L61 |
A62' |
A63' |
A64' |
A65' |
A66' |
A67' |
| L70 |
L71 |
A72' |
A73' |
A74' |
A75' |
A76' |
A77' |
|
|
ö
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
ø |
Puis, toujours à k=1:
æ
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
è |
| P0 |
P1 |
P2: r; u1,2 |
P3: r; u1,3 |
P0: r; u1,4 |
P1 |
P2 |
P3 |
|
| U00 |
U01 |
U02 |
U03 |
U04 |
U05 |
U06 |
U07 |
| L10 |
U11 |
U12 |
U13 |
U14 |
A15' |
A16' |
A17' |
| L20 |
L21 |
A22'' |
A23'' |
A24'' |
A25' |
A26' |
A27' |
| L30 |
L31 |
A32'' |
A33'' |
A34'' |
A35' |
A36' |
A37' |
| L40 |
L41 |
A42'' |
A43'' |
A44'' |
A45' |
A46' |
A47' |
| L50 |
L51 |
A52'' |
A53'' |
A54'' |
A55' |
A56' |
A57' |
| L60 |
L61 |
A62'' |
A63'' |
A64'' |
A65' |
A66' |
A67' |
| L70 |
L71 |
A72'' |
A73'' |
A74'' |
A75' |
A76' |
A77' |
|
|
ö
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
ø |
Faisons un calcul de complexité dans le cas particulier p=n.
Donc, ici, alloc(k)==k.
Le coût de la mise à jour (update) de la colonne j par le processeur j
est de
n-k-1 pour l'étape k (éléments en position k+1 à n-1).
Ceci étant fait pour toutes les étapes k=0 à k=n-1.
D'où un coût total de
Pour ce qui est du temps de calcul;
le chemin critique d'exécution est:
prep0(0)® update1(0,1), prep1(1) ® update2(1,2), prep2(2) ® ...
C'est comme si on faisait environ r fois le travail dans le cas d'une
allocation cyclique pour r=n/p processeurs.
Remarquez que l'on obtient bien un recouvrement des communications, mais pas entre
les communications et le calcul! C'est ce que l'on va améliorer dans la prochaine version
de l'algorithme distribué.
On a donc les coûts suivants:
nb+n2/2tc+O(1) pour les n-1 communications (transportant de l'ordre de
n2 données),
n2/2ta+O(1) pour les prep et
pour l'update des r colonnes sur le processeur j mod p, en parallèle sur tous les
processeurs,
environ rn(n-1)/2.
On obtient donc un coût final de l'ordre de n3/2p pour les update des p processeurs: c'est le terme dominant
si p<<n et l'efficacité est excellente asymptotiquement (pour n grand).
10.2.2 Recouvrement communication/calcul
On peut décomposer le broadcast afin de réaliser un meilleur recouvrement
entre les communications et le calcul, comme suit:
q = my_num();
p = tot_proc_num();
l = 0;
for (k=0;k<n-1;k++) {
if (k == q mod p) {
prep(k): for (i=k+1;i<n;i++)
buffer[i-k-1] = -a[i,l]/a[k,l];
l++; send(buffer,n-k); }
else { receive(buffer,n-k);
if (q != k-1 mod p) send(buffer,n-k); }
for (j=l;j<r;j++)
update(k,j): for (i=k+1;k<n;k++)
a[i,j] = a[i,j]+buffer[i-k-1]*a[k,j]; }
Il reste néanmoins un défaut.
Regardons ce qui se passe sur P1:
-
A l'étape k=0: P1 reçoit la colonne pivot 0 de P0
- P1 l'envoit à P2
- Fait update(0,j) pour toutes les colonnes j qui lui appartiennent, c'est-à-dire j=1 mod p
- A l'étape k=1: fait prep(1)
- Envoie la colonne pivot 1 à P2
- Fait update(1,j) pour toutes les colonnes j qui lui appartiennent, c'est-à-dire j=1 mod p
- etc.
On obtient donc les actions en parallèle suivantes, au cours du temps:
| P0 |
P1 |
P2 |
P3 |
| prep(0) |
|
|
|
| send(0) |
receive(0) |
|
|
| update(0,4) |
send(0) |
receive(0) |
|
| update(0,8) |
update(0,1) |
send(0) |
receive(0) |
| update(0,12) |
update(0,5) |
update(0,2) |
update(0,3) |
| |
update(0,9) |
update(0,6) |
update(0,7) |
| |
update(0,13) |
update(0,10) |
update(0,11) |
| |
prep(1) |
update(0,14) |
update(0,15) |
| |
send(1) |
receive(1) |
|
| |
update(1,5) |
send(1) |
receive(1) |
| receive(1) |
update(1,9) |
update(1,2) |
send(1) |
| update(1,4) |
update(1,13) |
update(1,6) |
update(1,3) |
| update(1,8) |
|
update(1,10) |
update(1,7) |
| update(1,12) |
|
update(1,14) |
update(1,11) |
| ... |
... |
... |
... |
Alors que
P1 aurait pu faire:
-
update(0,1)
- prep(1)
- Envoi vers P2
- update(0,j) pour j=1 mod p et j>1
- etc.
Et on obtiendrait, toujours sur quatre processeurs:
| P0 |
P1 |
P2 |
P3 |
| prep(0) |
|
|
|
| send(0) || up(0,4) |
receive(0) |
|
|
| up(0,8) |
send(0) || up(0,1) |
receive(0) |
|
| up(0,12) |
prep(1) |
send(0) || up(0,2) |
receive(0) |
| |
send(1) || up(0,5) |
receive(1) || up(0,6) |
up(0,3) |
| |
up(0,9) |
send(1) || up(0,10) |
receive(1) || up(0,7) |
| receive(1) |
up(0,13) |
up(0,14) |
send(1) || up(0,11) |
| up(1,4) |
up(1,5) |
up(1,2) |
up(0,15) |
| up(1,8) |
up(1,9) |
prep(2) |
up(1,3) |
| up(1,12) |
up(1,13) |
send(2) || up(1,6) |
receive(2) || up(1,7) |
| receive(2) |
|
up(1,10) |
send(2) || up(1,11) |
| send(2) || up(2,4) |
receive(2) |
up(1,14) |
up(1,15) |
| ... |
... |
... |
... |
Ce qui est bien mieux!
10.3 Algorithmique sur grille 2D
On va maintenant examiner trois algorithmes classiques de produit de matrices
sur une grille 2D, les
algorithmes de Cannon,
de Fox,
et de Snyder.
On cherche donc à calculer
C=C+AB, avec A, B et C de taille N × N.
Soit p=q2: on dispose d'une grille de processeurs en tore de taille q × q. On
distribue les matrices par blocs: Pij stocke Aij, Bij
et Cij.
La distribution des données peut se faire,
par blocs, et/ou de façon cyclique. La distribution par blocs
permet d'augmenter le grain de calcul et d'améliorer l'utilisation
des mémoires hiérarchiques. La
distribution cyclique, elle, permet de mieux équilibrer la charge.
On définit maintenant une distribution cyclique par blocs, de façon générale.
On suppose que l'on souhaite répartir un vecteur à M composantes sur p processeurs, à chaque
entrée 0 £ m < M on va associer trois indices, le numéro de processeur 0 £ q < p
sur lequel se trouve cette composante, le numéro de bloc b et l'indice i dans ce bloc:
| m |
® |
| (q,b,i)= |
æ
ç
ç
è |
ë |
|
û, ë
|
|
û, m mod r |
ö
÷
÷
ø |
|
où r est la taille de bloc et T=rp.
Par exemple, un réseau linéaire par blocs (4 processeurs) avec
M=8, p=4, et r=8 (pour chaque colonne) donnerait la répartition suivante:
| 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
| 2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
| 3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
| 3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
0u encore, un réseau linéaire cyclique (4 processeurs) avec
M=8, p=4, r=4 (pour chaque colonne) donnerait:
| 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
| 3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
| 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
| 3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
Autre exemple, un réseau en grille 2D par blocs (4×4 processeurs) avec
M=8, p=4, r=8 en ligne et en colonne, donnerait:
| 0.0 |
0.0 |
0.1 |
0.1 |
0.2 |
0.2 |
0.3 |
0.3 |
| 0.0 |
0.0 |
0.1 |
0.1 |
0.2 |
0.2 |
0.3 |
0.3 |
| 1.0 |
1.0 |
1.1 |
1.1 |
1.2 |
1.2 |
1.3 |
1.3 |
| 1.0 |
1.0 |
1.1 |
1.1 |
1.2 |
1.2 |
1.3 |
1.3 |
| 2.0 |
2.0 |
2.1 |
2.1 |
2.2 |
2.2 |
2.3 |
2.3 |
| 2.0 |
2.0 |
2.1 |
2.1 |
2.2 |
2.2 |
2.3 |
2.3 |
| 3.0 |
3.0 |
3.1 |
3.1 |
3.2 |
3.2 |
3.3 |
3.3 |
| 3.0 |
3.0 |
3.1 |
3.1 |
3.2 |
3.2 |
3.3 |
3.3 |
Enfin, dernier exemple, un réseau en grille 2D par blocs cycliques, avec
M=8, p=4, r=4 en ligne et en colonne:
| 0.0 |
0.1 |
0.2 |
0.3 |
0.0 |
0.1 |
0.2 |
0.3 |
| 1.0 |
1.1 |
1.2 |
1.3 |
1.0 |
1.1 |
1.2 |
1.3 |
| 2.0 |
2.1 |
2.2 |
2.3 |
2.0 |
2.1 |
2.2 |
2.3 |
| 3.0 |
3.1 |
3.2 |
3.3 |
3.0 |
3.1 |
3.2 |
3.3 |
| 0.0 |
0.1 |
0.2 |
0.3 |
0.0 |
0.1 |
0.2 |
0.3 |
| 1.0 |
1.1 |
1.2 |
1.3 |
1.0 |
1.1 |
1.2 |
1.3 |
| 2.0 |
2.1 |
2.2 |
2.3 |
2.0 |
2.1 |
2.2 |
2.3 |
| 3.0 |
3.1 |
3.2 |
3.3 |
3.0 |
3.1 |
3.2 |
3.3 |
En pratique, les fonctions de calcul de produit matriciel (ou autres fonctions qu'on
voudrait typiquement mettre dans une librairie de calcul distribué) peuvent se faire
en
version centralisée ou distribuée. Dans la version centralisée,
les routines sont appelées avec les données et les résultats sur la machine hôte.
Cette version permet de minimiser le nombre de fonctions à écrire, et permet
de choisir la distribution des données la plus adaptée.
Mais, elle a un coût prohibitif si on enchaîne les appels.
Dans la version distribuée au contraire,
les données sont déjà distribuées, et le résultat l'est également.
Le passage à l'échelle est donc plus facile à obtenir,
par des fonctions de redistribution des données.
Mais il y a un compromis à trouver entre le coût de redistribution
plus le coût de l'algorithme avec
rangement adapté, avec le coût de l'algorithme avec un rangement non-adapté.
De façon générale, la redistribution des données est parfois incontournable, avec
des coûts potentiellement dissuasifs.
Par exemple, si on dispose
d'une FFT 1D, programmer une FFT 2D peut se faire en enchaînant les calculs sur les lignes
d'une matrice, puis sur les colonnes de la matrice ainsi obtenue (ou l'inverse). Chacune des étapes
est parfaitement parallèle, car le calcul des FFT 1D sur l'ensemble des lignes peut se faire avec
une efficacité 1, en allouant une ligne (ou plus généralement un paquet de lignes) par processeur.
Par contre, quand on veut faire la même chose ensuite par colonne, il faut calculer la transposée de la
matrice, ou dit de façon plus prosaïque, il faut réorganiser la matrice, afin qu'à chaque processeur
soit maintenant associé une colonne, ou un paquet de colonnes en général. Ceci implique une diffusion globale
qui peut être extrêmement couteuse, et arriver aux limites de la contention du réseau, ou du bus de
données interne.
Prenons un exemple pour le reste des explications algorithmiques de cette section. On
va supposer n=4, et C=0. On cherche donc à calculer:
æ
ç
ç
ç
è |
| C00 |
C01 |
C02 |
C03 |
| C10 |
C11 |
C12 |
C13 |
| C20 |
C21 |
C22 |
C23 |
| C30 |
C31 |
C32 |
C33 |
|
ö
÷
÷
÷
ø |
|
¬ |
æ
ç
ç
ç
è |
| A00 |
A01 |
A02 |
A03 |
| A10 |
A11 |
A12 |
A13 |
| A20 |
A21 |
A22 |
A23 |
| A30 |
A31 |
A32 |
A33 |
|
ö
÷
÷
÷
ø |
|
× |
æ
ç
ç
ç
è |
| B00 |
B01 |
B02 |
B03 |
| B10 |
B11 |
B12 |
B13 |
| B20 |
B21 |
B22 |
B23 |
| B30 |
B31 |
B32 |
B33 |
|
ö
÷
÷
÷
ø |
|
10.3.1 Principe de l'algorithme de Cannon
Le pseudo-code pour l'algorithme de Cannon est:
/* diag(A) sur col 0, diag(B) sur ligne 0 */
Rotations(A,B); /* preskewing */
/* calcul du produit de matrice */
forall (k=1; k<=sqrt(P)) {
LocalProdMat(A,B,C);
VerticalRotation(B,downwards);
HorizontalRotation(A,leftwards); }
/* mouvements des donnees apres les calculs */
Rotations(A,B); /* postskewing */
Expliquons sur notre exemple comment l'algorithme de Cannon fonctionne.
On commence par effectuer un ``preskewing'', pour obtenir les allocations des données
suivantes:
æ
ç
ç
ç
è |
| C00 |
C01 |
C02 |
C03 |
| C10 |
C11 |
C12 |
C13 |
| C20 |
C21 |
C22 |
C23 |
| C30 |
C31 |
C32 |
C33 |
|
ö
÷
÷
÷
ø |
|
= |
æ
ç
ç
ç
è |
| A00 |
A01 |
A02 |
A03 |
| A11 |
A12 |
A13 |
A10 |
| A22 |
A23 |
A20 |
A21 |
| A33 |
A30 |
A31 |
A32 |
|
ö
÷
÷
÷
ø |
|
× |
æ
ç
ç
ç
è |
| B00 |
B11 |
B22 |
B33 |
| B10 |
B21 |
B32 |
B03 |
| B20 |
B31 |
B02 |
B13 |
| B30 |
B01 |
B12 |
B23 |
|
ö
÷
÷
÷
ø |
|
Puis on fait une
rotation sur A et B:
æ
ç
ç
ç
è |
| C00 |
C01 |
C02 |
C03 |
| C10 |
C11 |
C12 |
C13 |
| C20 |
C21 |
C22 |
C23 |
| C30 |
C31 |
C32 |
C33 |
|
ö
÷
÷
÷
ø |
|
= |
æ
ç
ç
ç
è |
| A01 |
A02 |
A03 |
A00 |
| A12 |
A13 |
A10 |
A11 |
| A23 |
A20 |
A21 |
A22 |
| A30 |
A31 |
A32 |
A33 |
|
ö
÷
÷
÷
ø |
|
× |
æ
ç
ç
ç
è |
| B30 |
B01 |
B12 |
B23 |
| B00 |
B11 |
B22 |
B33 |
| B10 |
B21 |
B32 |
B03 |
| B20 |
B31 |
B02 |
B13 |
|
ö
÷
÷
÷
ø |
|
10.3.2 Principe de l'algorithme de Fox
Dans cet algorithme, on ne fait pas
de mouvement de données initiales.
On effectue des diffusions horizontales des diagonales de A (décalées vers la droite
à chaque itération)
et des rotations verticales de B (de bas en haut):
/* pas de mouvements de donnees avant les calculs */
/* calcul du produit de matrices */
broadcast(A(x,x));
forall (k=1; k<sqrt(P)) {
LocalProdMat(A,B,C);
VerticalRotation(B,upwards);
broadcast(A(k+x,k+x)); }
forall () {
LocalProdMat(A,B,C);
VerticalRotation(B,upwards); }
/* pas de mouvements de donnees apres les calculs */
Par exemple, toujours pour n=4:
æ
ç
ç
ç
è |
| C00 |
C01 |
C02 |
C03 |
| C10 |
C11 |
C12 |
C13 |
| C20 |
C21 |
C22 |
C23 |
| C30 |
C31 |
C32 |
C33 |
|
ö
÷
÷
÷
ø |
|
+= |
æ
ç
ç
ç
è |
| A00 |
A00 |
A00 |
A00 |
| A11 |
A11 |
A11 |
A11 |
| A22 |
A22 |
A22 |
A22 |
| A33 |
A33 |
A33 |
A33 |
|
ö
÷
÷
÷
ø |
|
× |
æ
ç
ç
ç
è |
| B00 |
B01 |
B02 |
B03 |
| B10 |
B11 |
B12 |
B13 |
| B20 |
B21 |
B22 |
B23 |
| B30 |
B31 |
B32 |
B33 |
|
ö
÷
÷
÷
ø |
|
Puis:
æ
ç
ç
ç
è |
| C00 |
C01 |
C02 |
C03 |
| C10 |
C11 |
C12 |
C13 |
| C20 |
C21 |
C22 |
C23 |
| C30 |
C31 |
C32 |
C33 |
|
ö
÷
÷
÷
ø |
|
+= |
æ
ç
ç
ç
è |
| A01 |
A01 |
A01 |
A01 |
| A12 |
A12 |
A12 |
A12 |
| A23 |
A23 |
A23 |
A23 |
| A30 |
A30 |
A30 |
A30 |
|
ö
÷
÷
÷
ø |
|
× |
æ
ç
ç
ç
è |
| B10 |
B11 |
B12 |
B13 |
| B20 |
B21 |
B22 |
B23 |
| B30 |
B31 |
B32 |
B33 |
| B00 |
B01 |
B02 |
B03 |
|
ö
÷
÷
÷
ø |
|
10.3.3 Principe de l'algorithme de Snyder
On effectue une transposition préalable de B.
Puis, on fait à chaque étape des sommes globales sur les lignes de
processeurs (des produits calculés à chaque étape).
On accumule les résultats sur les diagonales (décalées à chaque étape vers la
droite) de C - représentées en gras dans les figures
ci-après.
Enfin, on fait des rotations verticales de B (de bas en haut, à chaque étape):
/* mouvements des donnees avant les calculs */
Transpose(B);
/* calcul du produit de matrices */
forall () {
LocalProdMat(A,B,C);
VerticalRotation(B,upwards); }
forall (k=1;k<sqrt(P)) {
GlobalSum(C(i,(i+k-1) mod sqrt(P)));
LocalProdMat(A,B,C);
VerticalRotation(B,upwards); }
GlobalSum(C(i,(i+sqrt(P)-1) mod sqrt(P)));
/* mouvements des donnees apres les calculs */
Transpose(B);
La encore, les premières étapes sont, pour n=4:
æ
ç
ç
ç
è |
| C00 |
C01 |
C02 |
C03 |
| C10 |
C11 |
C12 |
C13 |
| C20 |
C21 |
C22 |
C23 |
| C30 |
C31 |
C32 |
C33 |
|
ö
÷
÷
÷
ø |
|
+= |
æ
ç
ç
ç
è |
| A00 |
A01 |
A02 |
A03 |
| A10 |
A11 |
A12 |
A13 |
| A20 |
A21 |
A22 |
A23 |
| A30 |
A31 |
A32 |
A33 |
|
ö
÷
÷
÷
ø |
|
× |
æ
ç
ç
ç
è |
| B00 |
B01 |
B02 |
B03 |
| B10 |
B11 |
B12 |
B13 |
| B20 |
B21 |
B22 |
B23 |
| B30 |
B31 |
B32 |
B33 |
|
ö
÷
÷
÷
ø |
|
Puis:
æ
ç
ç
ç
è |
| C00 |
C01 |
C02 |
C03 |
| C10 |
C11 |
C12 |
C13 |
| C20 |
C21 |
C22 |
C23 |
| C30 |
C31 |
C32 |
C33 |
|
ö
÷
÷
÷
ø |
|
+= |
æ
ç
ç
ç
è |
| A00 |
A01 |
A02 |
A03 |
| A10 |
A11 |
A12 |
A13 |
| A20 |
A21 |
A22 |
A23 |
| A30 |
A31 |
A32 |
A33 |
|
ö
÷
÷
÷
ø |
|
× |
æ
ç
ç
ç
è |
| B10 |
B11 |
B12 |
B13 |
| B20 |
B21 |
B22 |
B23 |
| B30 |
B31 |
B32 |
B33 |
| B00 |
B01 |
B02 |
B03 |
|
ö
÷
÷
÷
ø |
|
10.4 Algorithmique hétérogène
Nous avons supposé jusqu'à présent que les différents processus parallèles
s'exécutent sur des processeurs qui ont exactement la même puissance de calcul. En général,
sur un cluster de PC, ce ne sera pas le cas: certaines seront plus rapides que d'autres. On va voir
maintenant comment faire en sorte de répartir au mieux le travail dans une telle situation.
On va considérer le problème suivant d'allocation statique de tâches. On suppose
que l'on se donne
t1,t2,...,tp les temps de cycle des processeurs, et que l'on a
B tâches identiques et indépendantes que l'on veut exécuter au mieux sur ces
p processeurs.
Le principe est que l'on va essayer d'assurer ci × ti = constante, donc on trouve:
| ci= |
ê
ê
ê
ê
ê
ê
ë |
|
ú
ú
ú
ú
ú
ú
û |
× B |
L'algorithme correspondant, qui calcule au mieux ces ci est le suivant :
Distribute(B,t1,t2,...,tn)
/* initialisation: calcule ci */
for (i=1;i<=p;i++)
c[i]=...
/* incrementer iterativement les ci minimisant le temps */
while (sum(c[])<B) {
find k in {1,...,p} st t[k]*(c[k]+1)=min{t[i]*(c[i]+1)};
c[k] = c[k]+1;
return(c[]);
On peut aussi programmer une version incrémentale de cet algorithme.
Le problème que résoud cet algorithme est plus complexe: on souhaite faire en sorte
que l'allocation soit optimale pour tout nombre d'atomes entre 1 et B.
Ceci se réalise par
programmation dynamique. Dans la suite, on donnera des exemples avec t1=3, t2=5 et t3=8.
L'algorithme est alors:
Distribute(B,t1,t2,...tp)
/* Initialisation: aucune tache a distribuer m=0 */
for (i=1;i<=p;i++) c[i]=0;
/* construit iterativement l'allocation sigma */
for (m=1;m<=B;m++)
find(k in {1,...p} st t[k]*(c[k]+1)=min{t[i]*(c[i]+1)});
c[k]=c[k]+1;
sigma[m]=k;
return(sigma[],c[]);
Par exemple, pour les valeurs de t1, t2 et t3 données plus haut, on trouve:
| # atomes |
c1 |
c2 |
c3 |
cout |
proc. sel. |
alloc. s |
| 0 |
0 |
0 |
0 |
|
1 |
|
| 1 |
1 |
0 |
0 |
3 |
2 |
s[1]=1 |
| 2 |
1 |
1 |
0 |
2.5 |
1 |
s[2]=2 |
| 3 |
2 |
1 |
0 |
2 |
3 |
s[3]=1 |
| 4 |
2 |
1 |
1 |
2 |
1 |
s[4]=3 |
| 5 |
3 |
1 |
1 |
1.8 |
2 |
s[5]=1 |
| ... |
|
|
|
|
|
|
| 9 |
5 |
3 |
1 |
1.67 |
3 |
s[9]=2 |
| 10 |
5 |
3 |
2 |
1.6 |
|
s[10]=3 |
10.4.1
LU hétérogène (1D)
A chaque étape, le processeur qui possède le bloc pivot le factorise
et le diffuse.
Les autres processeurs mettent à jour les colonnes restantes.
A l'étape suivante le bloc des b colonnes suivantes devient le
pivot.
Ainsi de suite: la taille des données passe de (n-1)× b
à (n-2)× b etc.
On a plusieurs solutions pour réaliser l'allocation statique
équilibrant les charges. On peut
redistribuer les colonnes restant à traiter à
chaque étape entre les processeurs: le problème devient alors le coût des communications.
On peut également essayer de trouver une allocation statique permettant un équilibrage de
charges à chaque étape.
On peut ainsi distribuer B tâches sur p processeurs de temps de cycle t1,
t2 etc. tp de telle manière à ce que
pour tout i Î {2,...,B}, le nombre de blocs de {i,...,B}
que possède chaque processeur Pj soit approximativement inversement
proportionnel à tj.
On alloue alors les blocs de colonnes périodiquement, dans motif de largeur B.
B est un paramètre, par exemple si la matrice est (nb)× (nb),
B=n (mais le recouvrement calcul communication est meilleur si B << n).
On utilise l'algorithme précédent en sens inverse: le bloc de colonne
1£ k £ B est alloué sur s(B-k+1).
Cette distribution est quasi-optimale pour tout sous-ensemble
[i,B] de colonnes.
Par exemple, pour
n=B=10, t1=3, t2=5, t3=8 le motif sera:
| P3 |
P2 |
P1 |
P1 |
P2 |
P1 |
P3 |
P1 |
P2 |
P1 |
10.4.2 Allocation statique 2D
Prenons l'exemple de la multiplication de matrices sur une grille homogène.
ScaLAPACK opère par un algorithme par blocs, avec une
double diffusion horizontale et verticale (comme à la figure 10.1).
Cela s'adapte au cas de matrices et de grilles. Il n'y a
aucune redistribution initiale des données.
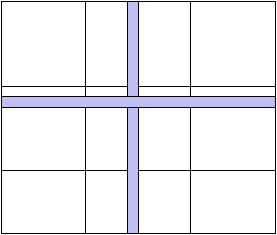
Figure 10.1: Diffusion horizontale et verticale, pour la multiplication de matrices sur une
grille homogène
Essayons d'allouer des blocs inhomogènes, mais de façon ``régulière''.
Le principe est d'allouer des rectangles de tailles différentes aux processeurs, en
fonction de leur vitesse relative. Supposons que l'on ait
p× q processeurs Pi,j de temps de cycle ti,j.
L'équilibrage de charge parfait n'est réalisable que si
la matrice des temps de cycle T=(ti,j) est
de rang 1.
Par exemple, dans la matrice de rang 2 suivante, P2,2 est partiellement inactif:
| |
1 |
|
| 1 |
t11=1 |
t12=2 |
|
t21=3 |
t22=5 |
Par contre, dans le cas d'une matrice de rang 1 comme ci-dessus, on arrive
à effectuer un équilibrage parfait:
| |
1 |
|
| 1 |
t11=1 |
t12=2 |
|
t21=3 |
t22=6 |
Le problème général revient à
optimiser:
-
Objectif Obj1:
| min |
|
maxi,j {ri × ti,j× cj} |
- Objectif Obj2:
| maxri × ti,j × cj £ 1 |
ì
í
î |
æ
ç
ç
è |
|
ri |
ö
÷
÷
ø |
× |
æ
ç
ç
è |
|
cj |
ö
÷
÷
ø |
ü
ý
þ |
De plus, l'hypothèse de régularité que nous avions faite, ne tient pas forcément.
En fait, la position des processeurs dans la grille n'est pas une donnée
du problème.
Toutes les permutations sont possibles, et il faut chercher la meilleure. Ceci nous
amène à un
problème NP-complet. En
conclusion: l'équilibrage 2D est extrêmement difficile!
10.4.3 Partitionnement libre
Comment faire par exemple avec p (premier) processeurs, comme à la figure
10.2 ?
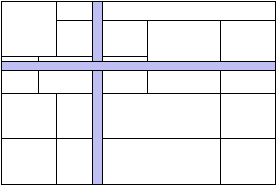
Figure 10.2: Problème de la partition libre
On suppose que l'on a
p processeurs de vitesses s1,s2,...,sn de somme 1 (normalisées).
On veut partitionner le carré unité en p rectangles de surfaces
s1,s2,...,sn.
La surface des rectangles représente la vitesse relative des processeurs.
La forme des rectangles doit permettre de minimiser les communications.
Géométriquement,
on essaie donc de partitionner le carré unité en p rectangles d'aires fixées
s1, s2, ..., sp afin de minimiser
soit la somme des demi-périmètres des rectangles dans le cas des
communications séquentielles,
soit le plus grand des demi-périmètres des rectangles dans le cas
de communications parallèles.
Ce sont deux
problèmes NP-complets.
Prenons un exemple pour bien mesurer la difficulté du partitionnement libre:
supposons que l'on ait p=5 rectangles R1,...,R5 dont les
aires sont s1=0.36, s2=0.25, s3=s4=s5=0.13 (voir figure 10.3).
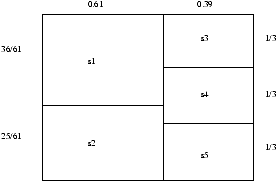
Figure 10.3: Problème de la partition libre
Alors, le
demi-périmètre maximal pour R1 est approximativement de 1.2002.
La borne inférieure absolue 2 sqrts1 = 1.2 est atteinte lorsque le
plus grand rectangle est un carré, ce qui n'est pas possible ici.
La somme des demi-périmètres est de 4.39.
La borne absolue inférieure åi=1p 2 sqrtsi=4.36 est atteinte
lorsque tous les rectangles sont des carrés.
Chapter 11 Systèmes tolérants aux pannes
Peut on ``implémenter'' certaines fonctions sur une architecture distribuée donnée,
même si des processeurs peuvent tomber en panne?
En fait, la réponse dépend assez finement de l'architecture, et des fonctions que l'on
cherche à implémenter. On verra qu'une fonction aussi simple que le consensus ne peut
pas être implémentée sur un système à mémoire partagée asynchrone (avec lecture et
écriture atomique). Ceci est un résultat relativement récent [FLP82]. La plupart
des autres résultats datent des années 90 pour les plus vieux.
11.1 Tâches de décision
Chaque problème que nous allons nous poser sera exprimé sous la forme suivante.
Pour chaque processeur
P0,...,Pn-1, on va se donner un ensemble de valeurs initiales possibles, pour le ou
les registres locaux à ces processeurs, dans un
domaine de valeurs K=IN ou
IR etc. Ceci formera un sous-ensemble I de Kn.
De façon similaire,
on se donne un ensemble de valeurs finales possibles
J dans Kn.
Enfin, on se donne une fonction, la fonction de décision
d: I ® Ã( J)
associant à chaque valeur initiale possible, l'ensemble des valeurs finales acceptables.
Prenons l'exemple classique du consensus (voir figure 11.1 et 11.2).
Chaque processeur démarre avec une valeur locale, ici un entier. Ceux-ci doivent ensuite
communiquer afin de se mettre tous d'accord sur une valeur. Cela veut dire que chacun doit terminer
son exécution, en temps fini, soit en ayant planté, soit en ayant une valeur locale qui est
une de celles qu'avait un des processeurs au début de l'exécution, et tous les autres processeurs
``vivants'' doivent avoir la même valeur locale.
Aux figures 11.1 et 11.2 on a trois processus, l'un avec la valeur 5, l'autre
avec 7 et enfin le troisième avec 11. Tous se mettent d'accord sur la valeur 7. Le consensus
est un problème essentiel dans les systèmes distribués tolérants aux pannes. Imaginez en effet
que l'on ait plusieurs unités de calcul qui doivent contrôler le même appareillage critique,
du fait que l'on ne peut pas se permettre qu'une panne vienne arrêter son bon fonctionnement. Il
faut néanmoins assurer une certaine cohérence des décisions faites par ces unités redondantes, et ceci
peut être fait, par exemple, en faisant en sorte que tous les processus encore vivants se mettent
d'accord sur une valeur de commande, que l'un au moins d'entre eux avait calculé. Bien sûr ceci
est une abstraction d'un problème en général bien plus complexe, mais la formulation du problème
du consensus permet de bien comprendre la difficulté de contrôle d'un système distribué, en
présence de pannes.
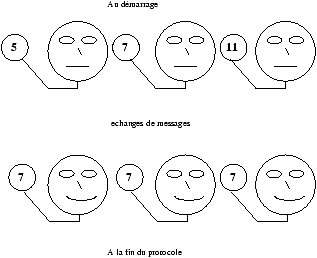
Figure 11.1: Le problème du consensus (sans panne).
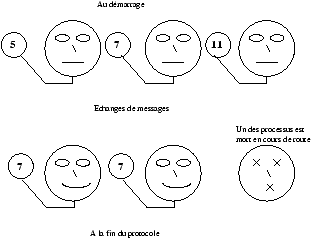
Figure 11.2: Le problème du consensus (avec panne).
Le problème du consensus se traduit formellement de la façon suivante:
-
K=IN, I=INn,
- J={(x,x,...,x) | x Î IN},
- d(x0,x1,...,xn-1)={
| {(x0,x0,...,x0), |
| (x1,x1,...,x1), |
| ..., |
| (xn-1,xn-1,...,xn-1)} |
.
11.2 ``Géométrisation'' du problème
On va voir que l'on peut donner aux ensembles de valeurs d'entrée et de sortie
une structure géométrique, généralisant celle de graphe, qui s'appelle un ensemble simplicial.
Selon le type d'architecture, toutes les fonctions ne pourront pas être
programmées, à cause de contraintes géométriques sur les fonctions de décision.
Ceci est en fait très similaire à des résultats classiques de géométrie, comme
le théorème du point fixe de Brouwer.
11.2.1 Espaces simpliciaux d'états
On va représenter les états des processeurs, à un instant donné de l'exécution de leur
protocole d'échange de données, de la façon suivante. On associera un point dans un
espace euclidien de dimension suffisante, à toute valeur locale que l'on trouvera sur un
processeur donné. Par exemple, l'unique point de la figure 11.3 représente
l'état du processeur P1, dans lequel l'entier local vaut 7.
L'état commun à deux processeurs, à un instant donné, sera représenté par l'arc
reliant les états locaux de chacun des deux processeurs, comme cela est montré par exemple
à la figure 11.4. Un ensemble d'états de deux processeurs sera représenté comme à
la figure 11.5: on a ici quatre états de la paire de processeurs P0, P1, un
dans lequel on a la valeur 0 sur P0 et 0 sur P1, un autre où P0 a la valeur
0 et P1 a la valeur 1, un troisième où P0 a la valeur 1 et P1 la valeur 0, et
enfin un dernier où P0 a la valeur 1 et P1 la valeur 1. Ce sont en fait les quatre
états initiaux possibles quand on a deux processeurs qui doivent résoudre le ``consensus
binaire'', c'est-à-dire le consensus dans le cas où les valeurs locales sont constituées d'un
seul bit. On remarquera que ce faisant, on a représenté les états initiaux par un graphe.
C'est le cas encore à la figure 11.6, qui décrit les deux états finaux possibles
du consensus binaire, ou à la figure 11.7 qui décrit les trois états finaux
possibles du ``pseudo-consensus'' binaire. Dans le cas du pseudo-consensus, on s'autorise un seul
des deux états possibles ou les deux processeurs n'ont pas la même valeur finale, mais pas
l'autre.
Figure 11.3: Un état local.

Figure 11.4: Un état composé de deux états locaux.
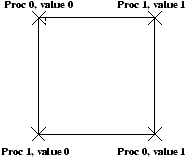
Figure 11.5: Etats initiaux pour le consensus binaire à deux processus.
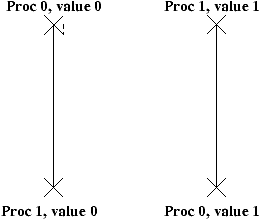
Figure 11.6: Etats finaux pour le consensus binaire à deux processus.
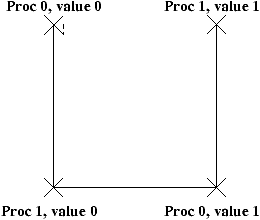
Figure 11.7: Etats finaux pour le pseudo-consensus binaire.
La généralisation de cette représentation des états des processeurs, sous forme de graphe,
est très simple. L'état global de trois processus sera représenté par l'enveloppe convexe
des trois points qui sont les états locaux de chacun des trois processus, comme à la figure
11.8. Pour n processus en général, l'état global sera représenté par
l'enveloppe convexe de n points distincts, ce que l'on appelle un n-simplexe: pour n=3
c'est un triangle, pour n=4 c'est un tétraèdre etc.
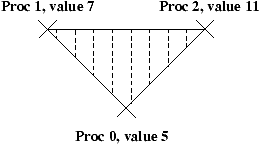
Figure 11.8: Etat global de trois processus.
De même que dans le cas n=2, certaines faces d'un n-simplexe, qui sont des m-simplexes,
c'est-à-dire qui représentent les états locaux d'un sous-groupe de m processeurs, peuvent
être communes à plusieurs n-simplexes, voir par exemple l'ensemble
d'états représenté géométriquement à la figure 11.9.
Ces collages de n-simplexes le long de leurs faces
sont ce que l'on appelle en général un ensemble simplicial. Il y a une très riche théorie
des ensembles simpliciaux, aussi bien combinatoire que topologique. En effet, on peut toujours
associer un ensemble simplicial à tout espace topologique, et à ``déformation'' près
(homotopie), la théorie des ensembles simpliciaux est équivalente à celle des espaces topologiques.
On utilisera plus loin des intuitions topologiques quand on aura à décrire certains ensembles
simpliciaux.
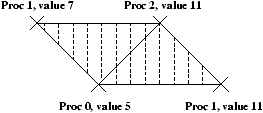
Figure 11.9: Ensemble d'états globaux.
Avec cette représentation des états, la spécification d'une tâche de décision devient
une relation ``graphique'' comme à la figure 11.10, dans le cas du consensus binaire.
Les états globaux en relations sont indiqués par les flèches en pointillé. Ainsi, le
``segment'' ((P,0),(Q,1)) peut être mis en relation par d avec ((P,0),(Q,0)) où
((P,1),(Q,1)).
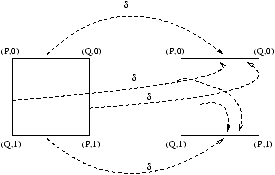
Figure 11.10: Spécification du consensus.
Un protocole est un programme fini, commençant avec des valeurs d'entrée, faisant
un nombre fixé d'étapes, et s'arrêtant sur une valeur de décision.
Le protocole à information totale est celui où la valeur locale est l'historique
complet des communications.
Le protocole ``générique'' est, en pseudo-code:
s = empty;
for (i=0; i<r; i++) {
broadcast messages;
s = s + messages received;
}
return delta(s);
A chaque tour de boucle correspond un ensemble d'états accessibles, représentés
géométriquement, comme aux figures
11.12, 11.13, 11.14. Ceci dépend essentiellement du modèle de communication
que l'on a, et sera développé dans deux cas aux sections 11.3 et 11.4.
11.2.3 Stratégie de preuve
Grâce à ces représentations géométriques, on va pouvoir déterminer si une tâche
de décision peut être implémentée ou pas sur une architecture, et si oui, combien d'échanges
de messages, ou d'écritures et lectures sont nécessaires pour résoudre le problème. Toutes
ces questions vont être résolues un peu de la même manière.
Il faut d'abord remarquer que la fonction delta dans le protocole générique, est, mathématiquement
parlant,
une fonction d: P ® O allant du protocole à information totale au complexe de sortie. Cette fonction est en fait une fonction simpliciale (car elle
est définie sur les points, puis étendue sur les enveloppes convexes), c'est-à-dire que ``topologiquement''
(entre les réalisations géométriques, c'est-à-dire les représentations graphiques que
l'on en fait dans un espace Rn), ce sont les analogues de fonctions continues.
Elle doit également respecter la relation de spécification du problème
D, c'est-à-dire que pour tout x Î I, pour tout
y Î P(I), x D (d(y)).
On va essayer de trouver une obstruction topologique à l'existence d'une
telle fonction simpliciale (pour une étape k donnée).
Cela est résumé à la figure 11.11.
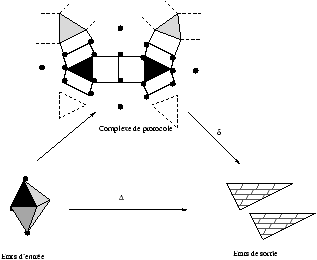
Figure 11.11: Stratégie de preuve.
Sans vouloir définir de façon générale ce que l'on entend par obstruction topologique,
il nous faut quand même expliciter les cas d'intérêt pour la suite de la formalisation.
Quand on dit ici obstruction topologique, cela veut dire obstruction à l'existence d'une
fonction continue f d'un espace topologique (typiquement ici ce sera la réalisation géométrique
d'un espace simplicial d'états) X vers un espace topologique Y vérifiant certaines conditions.
Par exemple, si on impose f(x0)=y0 et f(x1)=y1 avec x0 et x1 dans la même composante
connexe et y0 et y1 qui ne sont pas dans la même composante connexe, alors un tel
f continu ne peut pas exister (car l'image d'une composante connexe par une fonction continue est une composante connexe).
De même, si f va de la n-sphère pleine (le n-disque) vers la n-sphère vide, de telle
façon que f est l'identité sur la n-sphère vide, alors f ne peut pas être continue.
Cela est lié à la notion de n-connexité, qui est une généralisation de la connexité.
Déjà, la 1-connexité (ou simple connexité) est un invariant plus subtil que la connexité
(ou 0-connexité), par exemple
le cercle est connexe mais pas 1-connexe.
Dit de façon brève, la n-sphère vide est (n-1)-connexe (la 0-connexité correspond
à la connexité habituelle) et pas n-connexe, alors que la n-sphère pleine est
n-connexe.
11.3 Cas du modèle synchrone à passage de messages
Prenons l'exemple d'une architecture dans laquelle les informations transitent par
passage de message synchrone.
A chaque étape, chaque processeur diffuse sa propre valeur aux autres, dans n'importe
quel ordre. Chaque processeur reçoit les valeurs diffusées et calcule une
nouvelle valeur locale.
On va également supposer que l'on ne se préoccupe que des pannes ``crash'' des processeurs,
et non pas de pannes ``byzantines''. Une panne crash implique qu'un processeur n'envoie ni ne calcule plus
rien, de façon brusque. Par contre, lors d'une panne byzantine (que nous n'étudierons pas ici),
un processeur en panne continue à envoyer des données, mais qui n'ont éventuellement aucun sens.
Ces plantages peuvent arriver à n'importe quel moment, même en cours du broadcast.
A chaque protocole, on va associer un ensemble simplicial, de la même façon qu'on
l'a fait pour les entrées et les sorties, qui sera la représentation des états accessibles
depuis les états initiaux, à une étape donnée. C'est ce que l'on appelle le complexe
de protocole. De fait, cet ensemble simplicial est constitué de:
-
points: suites de messages reçus à une étape r
- simplexes: états composés à l'étape r
En fait, il s'agit d'un opérateur, prenant un état d'un certain nombre de processeurs,
et renvoyant les états accessibles après une étape. Il suffit ensuite d'itérer
cet opérateur afin de trouver les états accessibles après un nombre d'étapes quelconque.
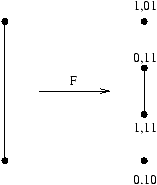
Figure 11.12: Complexe de protocole dans le cas synchrone (2 processus).
Dans le modèle synchrone, à l'étape 1 (voir la figure 11.12), soit
aucun processus n'est mort, donc tout le monde a reçu le message des autres (d'où
le segment central), soit un processus est mort, d'où les deux points comme états
possibles.
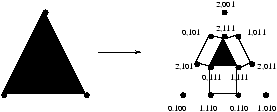
Figure 11.13: Complexe de protocole dans le cas synchrone (3 processus).
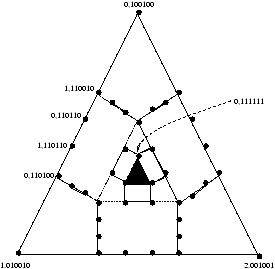
Figure 11.14: Complexe de protocole dans le cas synchrone, deuxième étape (3 processus).
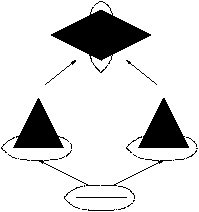
Figure 11.15: Collage de deux simplexes.
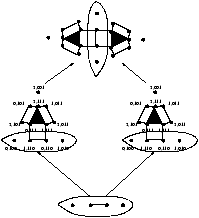
Figure 11.16: Construction du complexe de protocole par collage.
On va faire ici une application simple de cette stratégie de preuve.
On considère le problème du consensus binaire entre trois processus, dans le
modèle synchrone (et passage de messages)
Le complexe d'entrée est composé de 8 triangles:
(0,0,0), (0,0,1), (0,1,0),
(0,1,1), (1,0,0), (1,0,1), (1,1,0) et (1,1,1). Il est en fait homéomorphe
à une
sphère (une seule composante connexe):
les quatre premiers triangles déterminent l'hémisphère ``nord'' alors que les quatre
derniers déterminent l'hémisphère ``sud''.
Le complexe de sortie est composé de deux triangles: (0,0,0) et (1,1,1)
(donc, deux composantes connexes).
Considérons une seule étape de communication, comme à la figure 11.17. Le simplexe (0,0,0)
de l'hémisphère nord du complexe d'entrée se mappe sur la région du complexe de protocole entourée
de pointillés, à la figure 11.17. Alors que le simplexe (1,1,1) se mappe sur la région du complexe
de protocole entourée de pointillés, à la figure 11.18. Comme ces deux simplexes sont connexes
dans le complexe d'entrée, il est facile de démontrer que, après une étape, leurs images dans le complexe
de protocole sont aussi connexes. Or la fonction de décision d doit envoyer la première région sur
le simplexe (0,0,0) du complexe de sortie, et la deuxième région sur le simplexe (1,1,1) du complexe de sortie.
Comme on le voit à la figure 11.19, ceci est impossible car d doit être simpliciale (c'est à dire
continue en un certain sens), donc doit préserver la connexité, et ces deux simplexes ne sont pas connexes dans le
complexe de sortie! Cela prouve l'impossibilité dans ce modèle de résoudre le consensus en une étape.
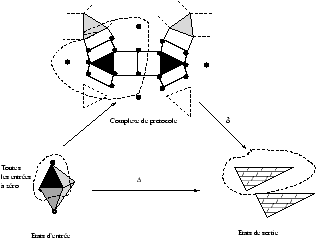
Figure 11.17: Application de la stratégie de preuve.
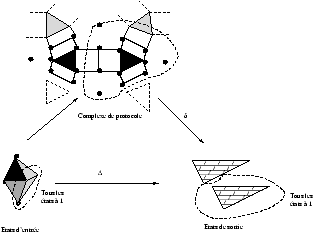
Figure 11.18: Application de la stratégie de preuve.
On considère au plus n-2 plantages, comme à la figure 11.19.
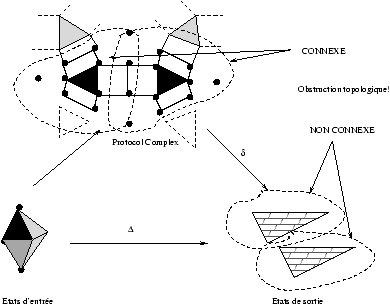
Figure 11.19: Application de la stratégie de preuve.
On peut prouver de façon plus générale que, dans tout complexe de protocole à
jusqu'à l'étape n-2, le sous-complexe où les processus ont tous 0 comme valeur
locale, et le sous-complexe où les processus ont tous 1 comme valeur locale, sont connexes.
Par le même raisonnement, il s'en suit aisément qu'on ne peut pas
résoudre le problème du consensus en moins de n-2 étapes.
De façon encore plus générale, dans le modèle par passage de message synchrone
où on s'autorise au plus k pannes, au bout de r étapes, on a
P(Sn-1) qui est (n-rk-2)-connexe.
Cela implique la borne de n-1 pour
résoudre le consensus
(pour k=1).
11.4 Cas du modèle asynchrone à mémoire partagée
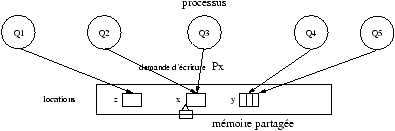
Figure 11.20: Une machine distribuée asynchrone à mémoire partagée
On suppose que l'on dispose d'une machine comme à la figure 11.20, dans laquelle
n processus partagent une mémoire de taille infinie, partitionnée de la manière suivante.
Chaque processus peut
écrire de façon atomique sur sa partie (update)
et lire de façon atomique toute la mémoire partagée dans sa propre mémoire locale.
C'est un modèle équivalent, en ce qui nous concerne, au modèle plus classique de
lecture/écriture atomique en mémoire partagée (sans partitionnement).
On cherche maintenant des protocoles sans attente, c'est-à-dire robustes
jusqu'à
n-1 pannes.
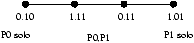
Figure 11.21: Le complexe de protocole dans le cas asynchrone (deux processus).
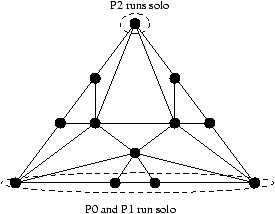
Figure 11.22: Le complexe de protocole dans le cas asynchrone (trois processus).
On a le théorème suivant, que l'on ne prouvera pas, et qui est du à Maurice
Herlihy et Sergio Rajsbaum (voir par exemple [HR00]):
Théorème
Les complexes de protocoles sans-attente, pour le modèle mémoire partagée asynchrone
avec lecture/écriture atomique sont
(n-1)-connexes (aucun trou en toutes dimensions)
quel que soit le nombre d'étapes considérées.
.2cm
On va faire une application de ce théorème au problème du k-consensus.
Il s'agit en fait d'une généralisation du problème du
consensus: les processus encore vivants doivent terminer leur exécution
avec au plus k valeurs différentes, prises dans l'ensemble des valeurs initiales.
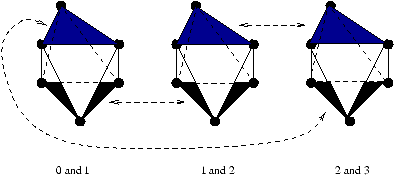
Figure 11.23: Complexe de sortie, pour n=3 et k=2.
Le complexe de sortie, illustré à la figure 11.23
est composé de 3 sphères collées ensemble, moins
le simplexe formé des 3 valeurs distinctes.
Il n'est pas simplement connexe.
On va utiliser un outil classique de la topologie algébrique combinatoire.
Commençons par
subdiviser un simplexe. On donne ensuite une couleur distincte à chaque coin
du simplexe.
Pour les autres points du bords du simplexe, on donne la couleur d'un des coins.
On colorie les points intérieurs par n'importe quelle couleur. Ceci est illustré
à la figure 11.24.
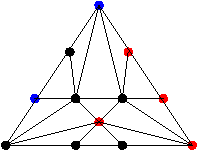
Figure 11.24:
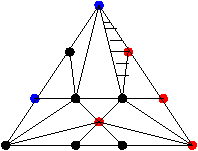
Figure 11.25:
Alors, comme illustré à la figure 11.25, il y a au moins un simplexe qui
possède toutes les couleurs (lemme de Sperner).
On va colorier chaque point des complexes d'entrée et de protocole de la façon suivante:
chaque processus est colorié avec la couleur correspondant à
son entrée.
Chaque point du complexe de protocole est colorié par sa décision.
Pour ce qui est du complexe de protocole, regardons comment se fait le coloriage en
petite dimension. Quand on considère l'exécution d'un seul processeur, la couleur
est imposée: en effet, le processus ne peut choisir que la couleur qu'il avait au départ.
Quand on considère l'exécution de deux processeurs, comme à la figure 11.26,
le complexe de protocole correspondant est connexe, et tous les points doivent être
d'une des deux couleurs de départ.
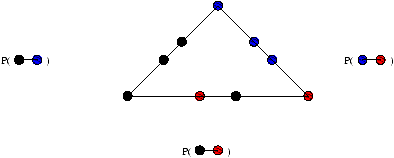
Figure 11.26: Coloriage du complexe de protocole en dimension 2.
De façon générale, comme le complexe de protocole est simplement connexe, on peut
``remplir'' l'intérieur des chemins combinatoires. Les coins du complexe de protocole sont
coloriés avec la valeur initiale sur ces processeurs (voir remarque en dimension 1).
Il nous reste seulement à appliquer le lemme de Sperner.
On en déduit qu'il existe un simplexe qui a toutes les 3 couleurs.
Ce simplexe correspondrait à une exécution du protocole dans laquelle les trois
processeurs décideraient trois valeurs différentes, ce qui contredit l'hypothèse
du 2-consensus!
En fait, on a un résultat très général concernant le modèle asynchrone:
Théorème
Une tâche de décision peut être calculée dans le modèle asynchrone si
et seulement si il existe une fonction simpliciale
µ allant d'une subdivision du complexe d'entrée vers le complexe de sorte, et qui
respecte la spécification
D.
Le principe de la preuve est le suivant.
Commençons par l'implication vers la droite.
On peut démontrer (en utilisant la suite exacte
de Mayer-Vietoris), que le complexe de protocole est, à chaque étape,
(n-1)-connexe.
Cela permet de plonger (par une fonction simpliciale)
n'importe quelle subdivision du complexe d'entrée dans le
complexe de protocole, pour une étape assez grande.
Enfin, on sait que si une tâche de décision peut être résolue, alors on a une
fonction simpliciale du complexe de protocole vers le complexe de sortie.
Dans l'autre sens, on peut prouver que l'on peut réduire n'importe quelle tâche de
décision au problème de l'accord (ou consensus) sur un simplexe. Ceci se fait en utilisant l'algorithme
du ``participating set'' de [BG93].
Cette tâche de décision commence par les coins d'un simplexe subdivisé, et doit
terminer sur les points d'un seul simplexe de la subdivision.
Montrons comment cela se passe avec deux processus.
Le programme suivant:
| P |
= |
update; |
P' |
= |
update; |
| |
|
scan; |
|
|
scan; |
| |
|
case (u,v) of |
|
|
case (u,v) of |
| |
|
(x,y'): u=x';update;[] |
|
|
(x,y'): v=y;update;[] |
| |
|
default: update |
|
|
default: update |
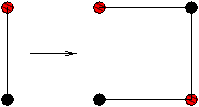
Figure 11.27: Subdivision d'un segment en trois segments.
Cela est facile à voir, en utilisant la sémantique des opérations de lecture/écriture
atomiques.
En fait, on n'a que trois traces intéressantes possibles, correspondant aux trois segments:
-
(i) Supposons que l'opération scan de P se termine avant
que l'opération update
de P' n'ai commencée: P ne connait pas y et il choisit donc d'écrire x
dans sa partition de la mémoire.
Prog termine avec l'état global ((P,x),(P',y)).
- (ii) Cas symétrique: Prog termine avec l'état global ((P,x'),(P',y')).
- (iii) L'opération scan de P s'exécute après l'opération
update de P' et l'opération scan de P' s'exécute après l'opération update de
P. Prog termine avec l'état global ((P,x'),(P',y)).
11.5 Autres primitives de communication
Les modèles vus précédemment sont un peu idéalisés. Les systèmes multi-processeurs
modernes offrent bien d'autres mécanismes de synchronisation:
test&set,
fetch&add,
compare&swap, files d'attentes etc.
A chacun de ces mécanismes nouveaux, correspond d'autres résultats (et bien sûr
d'autres complexes de protocoles). Par exemple, on peut résoudre le problème du consensus
entre deux processus, avec test&set, ou encore avec une file d'attente (avec
push et pop atomiques), voir [Lyn96].
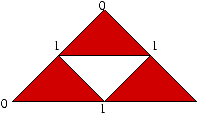
Figure 11.28: Complexe de protocole pour test&set, dans le cas de trois processus.
Dans le cas de test&set par exemple, les complexes de protocoles sont tous
(n-3)-connexes. On en déduit bien évidemment que le consensus entre deux processus
est implémentable, et donc que c'est une primitive ``plus puissante'' que la lecture/écriture
atomique. Mais on en déduit aussi assez facilement que le consensus entre trois processus
n'est pas implémentable.
11.6 Quelques références
Ce domaine démarre vraiment en 1985 avec la preuve de Fisher, Lynch et Patterson
(``FLP''), qu'il existe des tâches de décision simples qui ne peuvent pas être
implémentées sur un système simple de passage de messages, quand on veut qu'elles
soient robustes à une panne crash.
Plus tard, ce sont
Biran, Moran et Zaks à PoDC'88 qui trouveront la caractérisation
des tâches de décision qui peuvent être implémentées sur un
système simple de passage de messages, en s'autorisant jusqu'à une panne crash.
L'argument utilise une notion de
``similarity chain'' que l'on pourrait concevoir comme étant une version unidimensionnelle
des arguments que nous avons développés précédemment.
Puis à
PoDC'1993, et de façon indépendante,
Borowsky et Gafni, Saks et Zaharoglou et enfin Herlihy et Shavit
ont trouvé des bornes inférieures pour le problème du k-consensus
(d'abord proposé par
Chaudhuri en 1990).
Cette borne est en général de
ë f/k û + 1 étapes dans le modèle synchrone.
Nous avons essentiellement suivi ici les méthodes de preuve de Herlihy et Shavit.
Après cela,
Attiya, BarNoy, Dolev et Peleg ont pu caractériser la tâche de renommage,
dans JACM 1990.
Cette tâche, ou plus généralement la tâche de
(n+1,K)-renommage commence avec n+1 processus qui ont chacun un nom unique dans
0,...,N. On leur demande de se communiquer des informations afin
de changer leur nom, en un nom unique dans
0,...,K avec n£ K <N.
Ils ont montré que dans le modèle passage par messages, il y a une solution
sans attente pour
K³ 2n+1, et aucune pour K £ 2n.
Herlihy et Shavit dans STOC'93 ont prouvé que ce résultat est encore
valide dans le modèle asynchrone (ce qui leur a valu le prix Gödel en 2004).
La caractérisation complète des tâches de décision calculables sans attente
dans le
modèle asynchrone se trouve dans
``The topological structure of asynchronous
computability'', M. Herlihy and N. Shavit, J. of the ACM, 2000.
On reporte le lecteur au livre très complet de Lynch, ``Distributed Algorithms''
(1996) pour plus de détails.
Disons enfin que la représentation géométrique utilisée dans ce chapitre et celle
des ``progress graphs'' brièvement développée à la section 5.4.2 est liée,
voir par exemple [Gou03].
References
- [Abi00]
-
S. Abiteboul.
Bases de données, cours de l'Ecole Polytechnique, 2000.
- [BG93]
-
E. Borowsky and E. Gafni.
Generalized FLP impossibility result for t-resilient asynchronous
computations.
In Proc. of the 25th STOC. ACM Press, 1993.
- [CC77]
-
P. Cousot and R. Cousot.
Abstract interpretation: A unified lattice model for static analysis
of programs by construction of approximations of fixed points.
Principles of Programming Languages 4, pages 238--252, 1977.
- [Cou90]
-
P. Cousot.
Methods and Logics for Proving Programs.
Elsevier Science Publishers B.V. (North-Holland), 1990.
- [Dij68]
-
E.W. Dijkstra.
Cooperating Sequential Processes.
Academic Press, 1968.
- [FLP82]
-
M. J. Fischer, N. A. Lynch, and M. S. Paterson.
Impossibility of distributed consensus with one faulty process.
Technical Report MIT/LCS/TR-282, Massachusetts Institute of
Technology, September 1982.
- [GNS00]
-
E. Goubault, F. Nataf, and M. Schoenauer.
Calcul parallèle, 2000.
- [Gou03]
-
E. Goubault.
Some geometric perspectives in concurrency theory.
Homology Homotopy and Applications, 2003.
- [Gun94]
-
J. Gunawardena.
Homotopy and concurrency.
In Bulletin of the EATCS, number 54, pages 184--193, October
1994.
- [Hoa74]
-
C.A.R. Hoare.
Monitors: an operating system structuring concept.
Communication of the ACM, 17, 1974.
- [HR00]
-
M. Herlihy and S. Rajsbaum.
A primer on algebraic topology and distributed computing.
In Lecture Notes in Computer Science, number 1000.
Springer-Verlag, 2000.
- [Lyn96]
-
N. Lynch.
Distributed Algorithms.
Morgan-Kaufmann, 1996.
- [OG75]
-
Susan S. Owicki and David Gries.
Proving properties of parallel programs: An axiomatic approach.
Technical Report TR75-243, Cornell University, Computer Science
Department, May 1975.
- [OW00]
-
S. Oaks and H. Wong.
Java Threads.
O'Reilly, 2000.
- [Ray97]
-
M. Raynal.
Algorithmique et Parallélisme, le problème de l'exclusion
mutuelle.
Dunod, 1997.
- [Rem00]
-
D. Remy.
Compilation, cours de l'Ecole Polytechnique, 2000.
- [RL03]
-
Y. Robert and A. Legrand.
Algorithmique Parallèle, Cours et problèmes résolus.
Dunod, 2003.
- [Rob00]
-
Y. Robert.
Algorithmique parallèle.
Technical report, Cours, Ecole Polytechnique, 2000.
- [RR]
-
D. Reilly and M. Reilly.
JAVA, Network Programming and Distributed Computing.
Addison-Wesley.
- [Win93]
-
G. Winskel.
The formal semantics of programming languages.
The MIT Press, 1993.
This document was translated from LATEX by
HEVEA.